7.29某运输问题的产销平衡表与单位运价
运筹学教材编写组《运筹学》课后习题-运输问题(圣才出品)

计算所有非基变量的检验数,如表 4-18 所示:
表 4-18
由 24 = 0 可得 c24 =17 ,所以当 c24 变为 17 时,此问题有无穷多最优调运方案。以 (A2, B4 ) 为调入格,作一闭回路,取不同的调入量对其进行调整可得到其它两个最优调运方
如表 4-5 所示:
2 / 19
圣才电子书 十万种考研考证电子书、题库视频学习平台
表 4-5
第一步:用伏格尔法求得初始可行解如表 4-6 所示: 表 4-6
第二步:用位势法进行最优解的检验。在对应于表 4-6 的数字格处填入单位运价,并增
加一行一列,在行中填入 vj ,在列中填入 ui 。令 u1 = 0 ,按照 ui + vj = cij ( i,j B )求出所 有的 ui 和 vj ,并依据 ij = cij − (ui + vj ) ( i,j N )计算所有空格处的检验数,计算结果如表 4-7 所示:
表 4-2 中,有 10 个基格,而理论上只应有 m+n-l=9 个,所以表 4-2 给出的调运方案 不能作为表上作业法的初始解。
4.2 判断下列说法是否正确。 (1)在运输问题中,只要任意给出一组含(m+n+1)个非零的{xij},且满足
,就可以作为一个初始基可行解; (2)表上作业法实质上就是求解运输问题的单纯形法; (3)如果运输问题单位运价表的某一行(或某一列)元素分别加上一个常数 k,最优 调运方案将不发生变化; (4)运输问题单位运价表的全部元素乘上一个常数 k(k>0),最优调运方案将不发生
如表 4-8 所示: 表 4-8
第一步:用伏格尔法求得初始可行解如表 4-9 所示: 表 4-9
4 / 19
7.29某运输问题的产销平衡表与单位运价
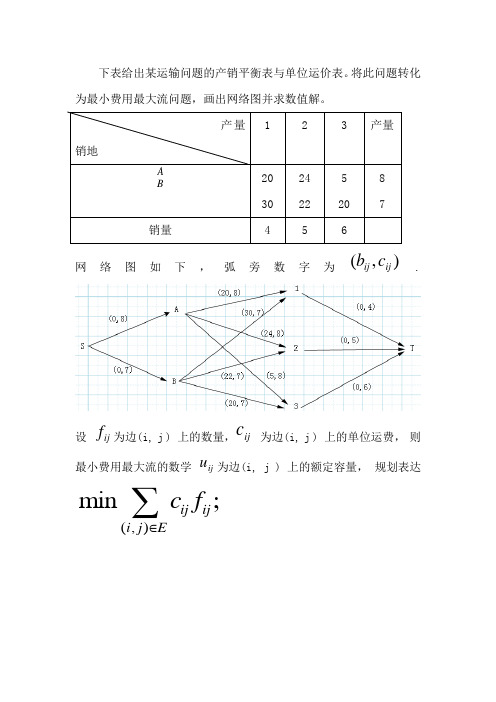
下表给出某运输问题的产销平衡表与单位运价表。
将此问题转化为最小费用最大流问题,画出网络图并求数值解。
产量销地123产量AB2030242252087销量456网络图如下,弧旁数字为(,)ij ijb c. 设ijf为边(i, j ) 上的数量,ij c为边(i, j ) 上的单位运费,则最小费用最大流的数学iju为边(i, j ) 上的额定容量,规划表达(,)min;ij iji j Ec f∈∑(,)(,),,0,,f ij ij f j V j V i j Ej i Ev i s f f v i ti s t ∈∈∈∈=⎧⎪-=-=⎨⎪≠⎩∑∑0,(,)ij ij f u i j E ≤≤∈sets :points/s,v1,v2,v3,v4,v5,t/; edge(points,points)/s,v1 s,v2 v1,v3 v1,v4 v1,v5 V2,v3 v2,v4 v2,v5 v3,t v4,t V5,t/:c,u,f; endsets data :c=0 0 20 24 5 30 22 20 0 0 0; u=8 7 8 8 8 7 7 7 4 5 6; vf=15; enddatamin =@sum (edge(i,j):c(i,j)*f(i,j));@for (points(i)|i#ne#@index (s) #and# i#ne#@index (t): @sum (edge(i,j):f(i,j))-@sum (edge(j, i):f(j,i))=0; ); @sum (edge(i,j)|i#eq#@index (s):f(i,j)) =vf; @sum (edge(j,i)|i#eq#@index (t):f(j,i)) =vf; @for (edge(i,j):@bnd (0,f(i,j),u(i,j))) ; endGlobal optimal solution found.Objective value: 240.0000 Total solver iterations: 1Variable Value Reduced Cost VF 15.00000 0.000000 C( S, V1) 0.000000 0.000000 C( S, V2) 0.000000 0.000000 C( V1, V3) 20.00000 0.000000 C( V1, V4) 24.00000 0.000000 C( V1, V5) 5.000000 0.000000 C( V2, V3) 30.00000 0.000000C( V2, V4) 22.00000 0.000000 C( V2, V5) 20.00000 0.000000 C( V3, T) 0.000000 0.000000 C( V4, T) 0.000000 0.000000 C( V5, T) 0.000000 0.000000 U( S, V1) 8.000000 0.000000 U( S, V2) 7.000000 0.000000 U( V1, V3) 8.000000 0.000000 U( V1, V4) 8.000000 0.000000 U( V1, V5) 8.000000 0.000000 U( V2, V3) 7.000000 0.000000 U( V2, V4) 7.000000 0.000000 U( V2, V5) 7.000000 0.000000 U( V3, T) 4.000000 0.000000 U( V4, T) 5.000000 0.000000 U( V5, T) 6.000000 0.000000 F( S, V1) 8.000000 -10.00000 F( S, V2) 7.000000 0.000000 F( V1, V3) 2.000000 0.000000 F( V1, V4) 0.000000 12.00000 F( V1, V5) 6.000000 0.000000 F( V2, V3) 2.000000 0.000000 F( V2, V4) 5.000000 0.000000 F( V2, V5) 0.000000 5.000000 F( V3, T) 4.000000 0.000000 F( V4, T) 5.000000 -8.000000 F( V5, T) 6.000000 -15.00000Row Slack or Surplus Dual Price1 240.0000 -1.0000002 0.000000 0.0000003 0.000000 -10.000004 0.000000 20.000005 0.000000 12.000006 0.000000 5.0000007 0.000000 -10.000008 0.000000 -20.00000结果其最小总费用为240。
昆明理工大学考研试题运筹学(2012-2016年)

费用 工作
A
B
C
D
E
人
甲
7
5
9
8
11
乙
9
12
7
11
9
丙
8
5
4
5
9
丁
7
3
6
9
6
戊
4
6
7
5
11
五、某施工单位有 500 台挖掘设备,在超负荷施工的条件下,年产值 20 万元/台,但其完好率仅 为 0.4;正常负荷下,年产值为 15 万元/台,完好率为 0.8。在 4 年内合理安排两种不同负荷 下施工的挖掘设备数量,使 4 年末仍有 160 台设备完好,并使产量最高。建立该问题的动态 规划基本方程。(15 分)
其最优单纯形表如表 2 所示。
问:(1)当 c1 由-1 变为 4 时,求新问题的最优解; (2)讨论 c2 在什么范围内变化时,原有的最优解仍是最优解。 表2
cj
CB
XB
b
-1
2
1
x1
x2
x3
0
0
x4
x5
1
x2
6
1
1
1
1
0
a
x5
10
3
0
1
1
1
cj-zj
-3
0
-1
-2
0
四、求解表 3 所示运输问题的最优调运方案。(25 分)
6.若原问题中 xi 为自由变量,那么对偶问题中的第 i 个约束一定为
A.等式约束
B.“≤”型约束
C.“≥”约束
D.无法确定
7.总运输费用最小的运输问题,若已得最优运输方案,则其中所有空格的检验数
解答运筹学运输问题作业

销地
产地
B1
B2
B3
产
B4
量
10
1
20
11
5
A1
10
15
12
7
9
20
A2
0
10
15
25
2
14
16
18
A3
5
5
销量
3c22 10
5
15
15
10 45
1 1 c 1 1 c 1 2 c 2 2 c 2 1 c 2 2 3
z i j 为第 i 年加班生产用于第 j 年交货的数量
约束条件:
x1 x2 x3 2 y11 y12 y13 2 z11 z12 z13 3 y 22 y 23 4 z 22 z 23 2 y 33 1 z33 3
生产能力限制
x1y11z11 3 x2y12z12y22z22 3 x3y13z13y23z23y33z33 4
1 3 c 1 3 c 2 3 c 2 2 c 1 2 c 2 2 1 0
2 4 c 2 4 c 2 2 c 1 2 c 1 4 1 0 c 2 2 3 2 c 3 2 c 3 1 c 2 1 c 2 2 2 4 c 2 2
3 4 c 3 4 c 1 4 c 1 2 c 2 2 c 2 1 c 3 1 1 8 c 2 2
10
15
20 25
A3
5
2
14
16
18
5
销量 5
15
15
10 45
a)从A2至B2的单位运价c22在什么范围变化时,上述最优调 运方案不变
深圳大学考研运筹学2021

深圳大学考研运筹学2021深圳大学硕士研究生入学考试试题第1页(共3页)2021深圳大学攻读硕士学位研究生入学考试试题招生专业:管理科学与工程考试科目:运筹学一、(26分)某厂生产三种产品,设生产量分别为x1,x2,x3,已知收益最大化模型如下:maxZ?3x1?2x2?4x3s?t?2x1?x2?3x3?40(第一种资源)2x1?2x2?3x3?4(第二种资源) 8x?10 (产品1的生产能力限制)x1,x2,x3?0(1)以x4,x5,x6表示三个约束的不足变量,写出标准型。
(4分)(2)若用单纯形法计算到下面表格 xB x4 x2 x1 x1 0 0 1 0 x2 0 1 0 0 x3 3/2 3/2 0 1 x4 1 0 0 0 x5 -1/2 1/2 0 -1 x6 -1 -1 1 -1 b 6 14 10 -58 cj?zj 指出所表达的基本可行解,目标函数值。
(4分)(3)指出上面给出的解是否最优。
若不是,求出最优解和最优目标函数值。
(6分)(4)写出本规划的对偶规划,并求出它的最优解。
(4分)(5)若产品1的单位利润从3变为4,问最优方案是什么?此时的最大收益是多少?(4分)?40??46?????(6)若资源常数列向量b??48?变为b???60?,问原最优性是否改变?求出此时的最优?10??10?????方案和最大收益。
(4分)第2页(共3页)1 / 10深圳大学硕士研究生入学考试试题二、(24分)有A1,A2,A3三个工厂,要把生产的产品运往B1,B2,B3三个需求点。
若B1,B2,B3三个需求点需求量没有得到满足,则单位罚款费用为6,3,4。
各厂的供应量、各点的需求量以及单位运价如下表。
问应如何组织调运才能使总费用(运输费用和罚款费用之和)最小?单位运单需求点工厂 A1 A2 A3 需求量 B1 6 5 2 20 B2 4 7 5 40 B3 7 8 6 30 供应量 15 30 25 (1)请将此问题化为供需平衡的运输问题;(2)用最小元素法求(1)的一个初始调运方案;(3)判断(2)中的方案是否最优,并说明原因。
运输问题的求解方法

m
n 1
m
n
m
cij xij
i 1 j 1
且满足
n 1 xij ai (i 1,2,, m) j 1 m xij b j ( j 1,2,, n, n 1) i 1 xij 0(i 1,2,, m; j 1,2,, n, n 1)
(二)最优解的判别 计算非基变量(空格)的检验数,当所有 的检验数 cij CB B 1 Pij 0 时,为最优解。 求空格检验数的方法有:
闭回路法
以某一空格为起点找一条闭回路,用水 平或垂直线向前划,每碰到一数字格转900后, 继续前进,直到回到起始空格为止。
闭回路如图5.3.1的(a)、(b)、(c) 等所示。从每一个空格出发一定存在并且可以 找到唯一的闭回路。因为,m+n-1个数字格 (基变量)对应的系数向量是一个基,任一空 格(非基变量)对应的系数向量是这个基的线 性组合。
1
CB B
[u1 , u 2 , , u m ; v1 , v , , v n ]
2
而每一个决策变量Xij的系数向量 P ei em j ,所以 ij
c ij (ui v j ) 0
(i, j B)
由单纯形法可知,所有基变量的检验数等于0,即
ij cij CB B 1 Pij c ij (ui v j )
第2步,在表5.3.5未划去的元素中再找出 最小运价为2,确定A2多余的1 t物资供应B3 。 得表5.3.6。将表5.3.5的行运价划去,得表5.3.7。
表5.3.6
销地
产地
A1 A2 A3 销量 销地
深圳大学考研运筹学2014-2016历年真题
第1页(共3页)2014深圳大学攻读硕士学位研究生入学考试试题招生专业:管理科学与工程 考试科目:运筹学一、(26分)某厂生产三种产品,设生产量分别为123,,x x x ,已知收益最大化模型如下:123max 324Z x x x =++s t ⋅⋅1232340x x x ++≤(第一种资源)12322348x x x ++≤(第二种资源)10x ≤ (产品1的生产能力限制)1230x x x ≥,,(1)以456,,x x x 表示三个约束的不足变量,写出标准型。
(4分)指出所表达的基本可行解,目标函数值。
(4分)(3)指出上面给出的解是否最优。
若不是,求出最优解和最优目标函数值。
(6分) (4)写出本规划的对偶规划,并求出它的最优解。
(4分)(5)若产品1的单位利润从3变为4,问最优方案是什么?此时的最大收益是多少?(4分)(6)若资源常数列向量404810b ⎛⎫ ⎪= ⎪ ⎪⎝⎭变为466010b ⎛⎫⎪'= ⎪ ⎪⎝⎭,问原最优性是否改变?求出此时的最优方案和最大收益。
(4分)第2页(共3页)二、(24分)有123,,A A A 三个工厂,要把生产的产品运往123,,B B B 三个需求点。
若123,,B B B 三个需求点需求量没有得到满足,则单位罚款费用为6,3,4。
各厂的供应量、各点的需求量以及单位运价如下表。
问应如何组织调运才能使总费用(运输费用和罚款费用之和)最小?(1)请将此问题化为供需平衡的运输问题; (2)用最小元素法求(1)的一个初始调运方案; (3)判断(2)中的方案是否最优,并说明原因。
三、(22分)设货车按泊松流到达车站,卸货后马上离开。
已知平均每天到达4辆车。
该货站有2位工人,同时为货车卸货,假设卸货时间服从负指数分布,平均每天可服务6辆车。
求:(1)该货站没有货车卸货的概率。
(4分) (2)在货站排队等候卸货的平均货车数。
(4分) (3)每辆车在货站的平均逗留时间。
运筹

运筹学复习题一、填空题1、运筹学主要研究_ 的问题,通过建立模型求解,为决策者进行决策提供科学依据。
2、可行域中任意两点间联结线段上的点均在可行域内,这样的点集叫 。
3、线形规划的标准形式有如下四个特点: 、 、 、 。
4、一个模型是m 个约束,n 个变量,则它的对偶模型为 个约束, 个变量。
5、为求解销量大于产量的运输问题,可虚设一个产地A m+1,它的销量等于_ 。
6、动态规划是解决 最优化问题的一种理论和方法。
二、单项选择题1、在用单纯形法求解某最大化问题时,如果检验数都小于等于零,而且非基变量的检验数全为负数,则表明此问题有( )。
A 、无穷多组最优解B 、无最优解C 、无可行解D 、唯一最优解2、互相对偶的两个线性规划问题,若其中一个无可行解,则另一个必定( )。
A 、无可行解 B 、有可行解C 、有最优解D 、有可行解,也可能无可行解3、运输问题求解时,m 个产地,n 个销地的初始调运表中,调运数字应该为( )。
A 、m+n 个 B 、m×n 个 C 、m+n -1个 D 、m+n+1个4、线性规划可行域的顶点是( )。
A 、可行解 B 、基本解 C 、基本可行解 D 、最优解5、如果目标规划要求实际值恰好达到目标值。
则相应的偏离变量应满足( )。
A 、d +>0B 、d +=0C 、min (d ++d -)D 、d ->0,d +>0 6、求解一般整数规划模型常用的方法是( )。
A 、分枝定界法B 、表上作业法C 、表上作业法和割平面法D 、单纯形法和表上作业法 7、下列说法错误的是( )。
A 、整数规划解的目标函数值一般优于其相应的线性规划问题解的目标函数值;B 、用割平面法求解纯整数规划时,要求包括松弛变量在内的全部变量必须取整数值;C 、指派问题数学模型的形式同运输问题十分相似,故也可以用表上作业法求解;D 、求解0-1规划的隐枚举法是分枝定界法的特例。
