模耦合理论及应用共24页
合集下载
《耦合理论》课件

有限差分法
总结词
有限差分法是一种将偏微分方程离散化 为差分方程的方法。
VS
详细描述
有限差分法通过将连续的时间和空间变量 离散化为有限个离散点,并使用差分近似 代替微分,将偏微分方程转化为离散的差 分方程组。然后,使用迭代或其他数值方 法求解该差分方程组,以获得近似解。
谱方法
总结词
谱方法是一种基于傅里叶级数或其它正交多 项式展开的数值方法。
详细描述
在电路中,耦合现象通常表现为信号的传递 和干扰。例如,变压器、电感和电容等元件 之间存在电磁耦合,这些耦合会导致信号的 传输和能量的损失。为了减小耦合效应,工 程师需要合理地设计电路布局和元件参数,
以优化电路性能。
建筑结构的耦合分析
总结词
建筑结构的耦合分析是指将结构视为一个整体,分析其各组成部分之间的相互作用和影 响。
02
根据影响和作用的范围,耦合可以分为局部耦合和全局耦合。局部耦合是指影 响和作用仅限于系统或组件的局部范围,而全局耦合则是指影响和作用遍及整 个系统或组件。
03
根据影响和作用的稳定性,耦合可以分为稳定耦合和不稳定耦合。稳定耦合是 指影响和作用在长时间内保持稳定,而不稳定耦合则是指影响和作用随时间变 化而变化。
时空耦合模型是指系统中各部分之间 的相互作用关系不仅与它们的状态变 量有关,还与时间和空间有关。
时空耦合模型在气候变化、地震预测 和城市规划等领域有广泛应用,例如 气候模式和城市交通网络等。
在时空耦合模型中,各部分之间的相 互作用力不仅与它们的状态变量成正 比,还与时间和空间有关,因此系统 状态的演化是时空相关的。
耦合的应用场景
01
在通信系统中,耦合可 以被用于描述信号传输 过程中的能量损失和干 扰现象。
第三章 模耦合理论及应用
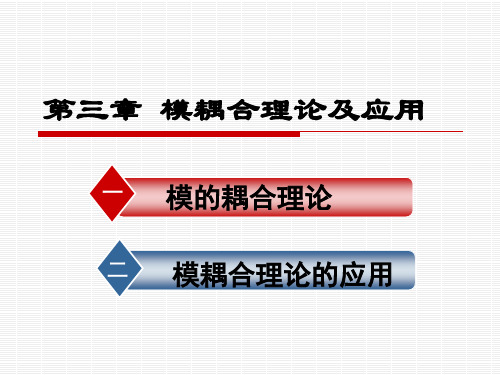
B ( z ) B e
A( z ) Ae e
e
A0 e B0 e
j 2 2 z j 2 2 z
e e
jz jz
Ae e j 2 2
2 2 z
A0
2 2
e
j 2 2 z
e
j ( b a ) z
表示两个模之间的耦合系数
表示两个模之间的相位匹配常数
3.1.1模耦合理论的基本概念—耦合方程
ab c f f b dxdy
* a II
其积分范围是波导II 的截面
C是 a , b 归一化相关常数
3.1.2模耦合理论的基本概念—同向传输
3.1.1模耦合理论的基本概念—耦合方程
模耦合的基本思想:
有波导I和 II ,当它们离得充分远时,假设其 各自的简正模场分布为φaφb ,并分别以传输 常数βa βb进行传输,然后,将两个波导相互 靠近,简正模的场分布不再是φaφb,而是将 包含波导I、II 的整个体系看作是一个波导, 此时耦合波导体系中传输的将是两个新的简正 模φeφo传输常数φe φo 此是模耦合的基本 概念。 53页给出
同方向传输耦合
55页
模型图
a〉, b〉 , a〉 b 0 0
dA( z ) j ab B( z )e j ( b a ) z 已知耦合方程: dz dB( z ) j ba A( z )e j ( b a ) z dz
* ab ba 2 a - b
3.1.2模耦合理论的基本概念—同向传输
则将模耦合方程求解得到:
A( z )
B( z ) e
耦合模理论-coupled mode theory

Lecture 6: Coupled-mode theory
Mode expansion Single-waveguide mode coupling Multiple-waveguide mode coupling Two-mode coupling Codirectional coupling Contradirectional coupling Phase matching
References: This lecture follows the materials from Photonic Devices, Jia-Ming Liu, Chapter 4.
1
Coupled-mode theory
Coupled-mode theory deals with the coupling of spatial modes of different spatial distributions or different polarizations, or both. The normal mode fields spatial dependence in a lossless waveguide at a single frequency can be given as
ˆ ( x, y ) exp(i z ) E (r ) A ( z ) E
ˆ ( x, y ) exp(i z ) H (r ) A ( z ) H
9
Single-waveguide mode coupling
10
Single-waveguide mode coupling
E i 0 H H iE iP
Mode expansion Single-waveguide mode coupling Multiple-waveguide mode coupling Two-mode coupling Codirectional coupling Contradirectional coupling Phase matching
References: This lecture follows the materials from Photonic Devices, Jia-Ming Liu, Chapter 4.
1
Coupled-mode theory
Coupled-mode theory deals with the coupling of spatial modes of different spatial distributions or different polarizations, or both. The normal mode fields spatial dependence in a lossless waveguide at a single frequency can be given as
ˆ ( x, y ) exp(i z ) E (r ) A ( z ) E
ˆ ( x, y ) exp(i z ) H (r ) A ( z ) H
9
Single-waveguide mode coupling
10
Single-waveguide mode coupling
E i 0 H H iE iP
光纤光栅模耦合理论

光纤光栅耦合模理论
折射率阶跃分布的均匀纤芯单模光纤中,场的分布可分为三种模闭在纤芯内,包层内的电磁场按指数迅速衰减。 包层模:包层内的电磁场成为沿径向方向的振荡解,能量分布分立。
辐射模:外辐射的能量。
光纤光栅耦合模理论
当某一模式光波在光纤中传至光栅部位并满足布喇格条件时,每
1 j0
2 t Emt ) j m ( z H mt ) j 0 n0 Emt
............ ........... ...........
光纤光栅耦合模理论
各本征模均遵从麦克斯韦方程
t (
1 j0
1
2 t Emt ) j m ( z H mt ) j 0 n0 Emt
的宽度(FWHM)。
问题10:带宽
光纤光栅模式耦合理论
光纤光栅区域的光场满足模式耦合方程:
dA z z k z B z exp i q z dz dz 0 z dB z dz k z A z exp i q z dz 0
单模均匀光纤光栅反射谱公式: 光纤光栅布喇格反射公式
光纤光栅耦合模理论
光纤光栅区域的光场满足模式耦合模方程:
dAin0 dz dAin0 dz K n0 m0 Aim0 exp[ j ( n0 m0 ) z ] K n0 m0 Aim0 exp[ j ( n0 m0 ) z ]
简化方程
z dA z k z B z exp[i q z dz ] dz 0 z dB z k z A z exp[i q z dz ] dz 0
折射率阶跃分布的均匀纤芯单模光纤中,场的分布可分为三种模闭在纤芯内,包层内的电磁场按指数迅速衰减。 包层模:包层内的电磁场成为沿径向方向的振荡解,能量分布分立。
辐射模:外辐射的能量。
光纤光栅耦合模理论
当某一模式光波在光纤中传至光栅部位并满足布喇格条件时,每
1 j0
2 t Emt ) j m ( z H mt ) j 0 n0 Emt
............ ........... ...........
光纤光栅耦合模理论
各本征模均遵从麦克斯韦方程
t (
1 j0
1
2 t Emt ) j m ( z H mt ) j 0 n0 Emt
的宽度(FWHM)。
问题10:带宽
光纤光栅模式耦合理论
光纤光栅区域的光场满足模式耦合方程:
dA z z k z B z exp i q z dz dz 0 z dB z dz k z A z exp i q z dz 0
单模均匀光纤光栅反射谱公式: 光纤光栅布喇格反射公式
光纤光栅耦合模理论
光纤光栅区域的光场满足模式耦合模方程:
dAin0 dz dAin0 dz K n0 m0 Aim0 exp[ j ( n0 m0 ) z ] K n0 m0 Aim0 exp[ j ( n0 m0 ) z ]
简化方程
z dA z k z B z exp[i q z dz ] dz 0 z dB z k z A z exp[i q z dz ] dz 0
光纤光栅模耦合理论

单模均匀光纤光栅反射谱公式: 光纤光栅布喇格反射公式
光纤光栅耦合模理论
光纤光栅区域的光场满足模式耦合模方程:
dAin0 dz dAin0 dz K n0 m0 Aim0 exp[ j ( n0 m0 ) z ] K n0 m0 Aim0 exp[ j ( n0 m0 ) z ]
t Emt H mt H mz 考虑 j m H mt j0 z 是m模式的播常 H mt 2 m H m t H mz z j 0 n0 Em m zt t z
t (
A z 、B z 分别为光纤光栅区域中的前向波、后向波; k z 为耦合系数;q z 与光栅周期和传播常数 有关。
利用此方程和光纤光栅的折射率分布、结构参量及边界条件, 并借助数值算法,可以求出光纤光栅的光谱特性。
i t i 0 m i m mt i H t bi ' m H mt i ' 0 m
i i 2 t [ t (aim Emt )] z (bim H mt ) j 0 n aim Emt j0 z i0 m i0 m i0 m i
i i 2 t [ t (aim Emt )] z (bim H mt ) j 0 n aim Emt j0 z i0 m i0 m i0 m i
dbim )( z H mt ) j 0 (n 2 n0 2 )aim Emt ] 0 dz i 0 m i daim bim 1 1 {[( jb )( z E ) [( )( H i m m mt t t mt )]} 0 2 2 dz j n n i 0 m 0 0
第六章 模式耦合理论2016

K 21
6 17
上式说明了一个有趣的现象,光波功率在光纤1和光纤2之间周期性 sin 2 Kz 1 交换(结论二),如果 ,则光功率完全耦合到光纤 2中。
(6-15)式 和(6-16)式的结果只能说是耦合模方程的形式解,因为在所 得结果中,有两个重要的参数,即耦合参数K12和K21并未给出。 严格求解这两个系数是非常困难的,简化的过程如下。 如右图示,将整个光纤耦合系 统分成三个区域。 如前所述,弱耦合条件下,可 认为波导1和波导2内的场分别为
6 9
K12 和 K 21是耦合系数,它们直接决定了光纤1和光纤2之间相互影响
的大小。一般说来,耦合系数都是复数,并且可以采用Lorentz互易 定理证明它们具有如下互易特性
* K12 K 21
利用 (6-8)式和耦合方程(6-9)式,可以得到
dA1 z j z jK 21 A2 z e 1 2 dz dA2 z jK A z e j 2 1 z 12 1 dz
K 21 1 B a 1 2 1 K a2 B 1 a K 21 a 2 2 1 2 K
6 9
6 14
a2 0 如果再令初始条件 ,则可将上式简化为
j z a1 z a1 cos Kze j z a2 z a1 sin Kze
•2. 模式的横向耦合理论
到另一根光纤中光波场的影响。 为分析两根相互靠近的光纤 的影响,首先假设两根光纤单独 存在时的场量分别为 a.)只有波导1存在时
1 j z E10 e 1 E1 2 j z 1 E10 e 1 j z H10 e 1 H1 2 j z 1 H10 e
model coupling theory

model coupling theory模型耦合理论(Model Coupling Theory)是指将不同的模型或子模型通过某种方式相互连接,形成一个整体模型的理论和方法。
它旨在解决多个模型之间相互依赖、相互影响的问题,以及提高模型的准确性和可靠性。
模型耦合理论的基本思想是将多个模型组合成一个整体模型,使得各个子模型之间可以相互传递信息、相互影响,并通过协同作用达到更准确的结果。
模型耦合可以是线性的、非线性的,也可以是静态的、动态的。
在模型耦合理论中,常用的耦合方式有以下几种:1. 驱动-响应耦合(Driver-Response Coupling):一个模型作为主模型,驱动其他模型的运行,并根据其他模型的响应进行调整。
这种耦合方式常用于模拟系统的控制过程。
2. 数据耦合(Data Coupling):不同模型之间通过共享数据进行耦合。
模型之间的数据交换可以是单向的或双向的,可以是离散的或连续的。
3. 参数耦合(Parameter Coupling):不同模型之间通过共享参数进行耦合。
一个模型的输出可以作为另一个模型的输入参数,或者两个模型共享相同的参数。
4. 接口耦合(Interface Coupling):不同模型之间通过定义共同的接口进行耦合。
接口定义了模型之间的输入和输出,使得模型之间可以进行交互。
模型耦合理论的应用非常广泛,包括气候模型、生态模型、经济模型等领域。
通过将不同的模型耦合起来,可以更好地模拟和预测复杂系统的行为,提高决策的科学性和准确性。
然而,模型耦合也带来了一些挑战,如模型之间的数据一致性、模型之间的计算效率等问题,需要进一步研究和解决。
第三章 模耦合理论及应用3、2
§3.2 模耦合理论的应用—光纤定向耦合器
制作方法: 2×2定向耦合器大多采用熔融 拉锥的制造方法,在制作过程中,将两根光 纤胶合在一起,用火焰加热到软化温度后再 拉伸,在熔融区形成渐变双锥结构,拉锥后, 一方面两光纤彼此靠近,另一方面光纤芯径 减小,从而使光场由纤芯向外扩散,纤芯外 的场称为消失场。当两光纤极为靠近时,将 会通过消失场进行能量交换,产生两光纤之 间的耦合,耦合的程度取决于耦合区长度及 纤芯间包层的厚度。
2 (n12 k 02 k x2 k y )1 / 2 2 p x [(n12 n2 )k 02 k x2 ]1 / 2 2 2 p y [(n12 n2 )k 02 k y ]1 / 2 2 2 q y [(n12 n3 )k 02 k y ]1 / 2
1/ 2
, 2 1 2
§3.2 模耦合理论的应用—光纤定向耦合器
若耦合的两根光纤完全一致,且耦合的两模式相 位匹配,则可以得到两输出光场振幅及功率的表 达式 :
A( z ) A0 cos( z )
2
B( z ) iB0 sin( z )
2 p1 ( z ) A( z ) A0 cos2 ( z )
2 x
§3.2 模耦合理论的应用—矩形定向耦合器
举例: 设矩形波导定向耦合器的参数
n1 1.5, n2 1,515, n3 1,2a 5m,2b 1m,2c 1m, 632.8nm
可求得: kc 4cm1 ,即得耦合长度 LC / 2kc 3.9nm 由于耦合系数随 2c 的增大而指数式减小,所以间距 2c 发生微小变化, 可以影响耦合长度很大的变化. 例如: 上式中, Lc / 2c 7000,因此 间距 2c 发生 100nm 偏差将使耦合 长度 LC 改变 20% ,( Lc =0.7mm) 所以说明在制作给定耦合长度为
