最新平面几何100题前80题答案
新平面几何100题1-60

1、设I是△ABC的内心,D是边BC上的一点,E是BC延长线上一点,且满足BDDC =BEEC.设H是D到直线IE的垂足,证明:∠AHE=∠IDE.B2、设O、H分别是△ABC的外心和垂心,点A关于直线OH的对称点是P,点P和点A不在直线BC的同侧,E、F分别在AB和AC上,满足BE=PC,CF=PB,直线AP、OH相交于点K,证明:EK⊥FK.B CP3、设正△ABC的外接圆和内切圆分别是Γ、ω,P为ω上一动点,P1、P2、P3分别为P在BC、CA、AB上的射影,圆ω1、ω2、ω3分别与BC、CA、AB切于P1、P2、P3且与Γ内切(它们的圆心与A、B、C分别在BC、CA、AB的异侧).证明:圆ω1、ω2、ω3两两外公切线的长度之和是一个定值.A4、设正△ABC内接于⊙O,E、F分别是AC,BC上一点,使得AE=2CE,BF=2CF. P为⊙O上的一点,PD⊥EF于D,交AB于K,作PS⊥BC于S,连接SK并交AO于T.证明:DS=DT.T5、设E、F分别位于△ABC的AC,AB边上,BE、CF交于D,△AEF的外接圆交△ABC的外接圆于点A、P,△AEF的外接圆在A处的切线交△ABC于A、Q两点,设N、M分别为AQ、BC的中点.证明:∠APD=∠MNQ.Q6、已知△ABC的外心为O,A′、B′、C′分别是边BC、CA、AB上的点,且满足A、B′、C′、O共圆,C、A′、B′、O共圆.以B′为圆心,B′C为半径的圆和以C′为圆心,BC′为半径的圆的根轴为l a.类似定义l b、l c.证明:直线l a、l b、l c交出的三角形垂心与△ABC的垂心重合.7、设凸四边形ABCD顶点不共圆,记点A在直线BC、BD、CD上的射影分别为P、Q、R,其中P、Q分别在BC、BD内,R在CD的延长线上.记点D在直线AC、BC、AB上的射影分别为X、Y、Z,其中X、Y分别在线段AC、BC内,Z在BA的延长线上,设△ABD的垂心为H,证明:BH的中点在△PQR外接圆和△XYZ外接圆的根轴上.8、在圆内接四边形ABCD中,AB>BC,AD>DC,I、J分别为△ABC、△ADC的内心.以AC为直径的圆与线段IB交于点X、与JD的延长线交于点Y.证明:若B、I、J、D四点共圆,则点X、Y关于直线AC对称.9、设△ABC的外接圆和内切圆的圆心分别为O、I,点M和点Q分别在边AB和AC上,点N和点P分别在边BC上(N在线段BP上),且满足五边形AMNPQ的五条边长相等.记点S为直线MN和QP的交点,l为∠MSQ的角平分线.证明:l和OI平行.S11、凸四边形ABCD中,P、Q、R、S分别是线段AB、BC、CD、DA上的点.若相交的线段PR、QS把四边形ABCD分为4个四个对角线互相垂直的凸四边形.证明:P、Q、R、S四点共圆.B12、不等腰三角形ABC的外接圆为Ω,内心为I,射线AI与BC交于D,与Ω交于除A以外的另一点M,以DM为直径的圆与Ω交于除M以外的另一点K,直线MK与BC交于点S,设N为IS的中点,L1、L2为△KID的外接圆与△MAN的外接圆的交点.证明:IL1或IL2的中点在Ω上.S113、在非等腰△ABC中,D、E、F分别为BC、CA、AB的中点.过D作△ABC的内切圆的切线(不同于直线BC),交直线EF于点X.类似定义Y和Z.证明:X、Y、Z三点共线.ZBD14、圆外切四边形ABCD的内切圆⊙I分别切DC、DA于E、F,K为BD上一点,KA、KC分别交⊙I于M、N,MF与NE交于L.证明:L在直线BD上.L15、四边形ABCD内接于⊙O,∠A、∠C的角平分线相交于点I,∠B、∠D的角平分线相交于点J,直线IJ不经过点O,且与边AB、CD的延长线分别交于点P、R,与边BC、DA分别交于点Q、S.线段PR、QS的中点分别为M、N.证明:OM⊥ON.R16、在圆内接四边形ABCD中,M、N分别是线段BC、AD的中点,对角线AC、BD交于点E. P是边BC上的点,满足PBPC =(BDAC)2.设E在PN上的投影是H,证明:△BEC的外接圆与△MPH的外接圆相切.17、圆内接四边形ABCD的对角线相交于P,存在一个圆Γ与AB、BC、AD、DC的延长线切于点X、Y、Z、T.过A、B的圆Ω与圆Γ外切于S.证明:SP⊥ST.18、对于平面上的凸四边形ABCD,设直线l交直线AB于X,交直线CD于X′,交直线BC于Y,交直线DA于Y′,交直线AC于Z,交直线BD于Z′.已知以上六点在l上按照X、Y、Z、X′、Y′、Z′的顺序排列.证明:以XX′、YY′、ZZ′为直径的三个圆共点.19、设O是三角形ABC的外心,D是AB上一点,作与⊙O内切,与线段CD、BD相切的⊙I;作与⊙O内切,与线段CD、AD相切的⊙J.证明:若A、B、I、J四点共圆,则D是三角形ABC中的∠ACB内旁切圆在AB上的切点.20、设⊙O 1与⊙O 2交于P 、Q 两点,过P 作两条割线AB 、CD ,过Q 作两条平行割线A′B′、C′D′,取△PAC 、△PBD 、△QB′D′、△QA′C′的九点圆圆心F 1、F 2、F 3、F 4.证明:四边形F 1F 2F 3F 4是矩形.D'A'C21、设⊙O是四边形ABCD的内切圆. AC、BD交于P,I、J分别是△ABC、△ADC的内心,OP,IJ交于K,T是K在BD上的射影.证明:I、J、P、T四点共圆.B22、设O、I B、I C分别是锐角三角形ABC的外接圆圆心,∠B内的旁切圆圆心和∠C内的旁切圆圆心.在AC边上取点E和Y,使得∠ABY=∠CBY,BE⊥AC,在AB边上取点F和Z,使得∠ACZ=∠BCZ,CF⊥AB,直线I B F和I C E交于点P.证明:PO⊥YZ.I B I C23、四边形ABCD内接于⊙O,AC、BD交于点P,直线AB、CD交于点Q. K是P在QO上的射影,KP、BC交于X,M是BC的中点,P′是P关于BC的对称点,K′是K关于M的对称点. P′K′分别交BC于Y,交KP于Z.证明:△XYZ的外接圆与△QBC的外接圆相切.D24、对边不平行的凸四边形ABCD中,BA延长线与CD延长线交于点E,AD延长线与BC延长线交于点F,K是△CDF的外接圆与△ADE的外接圆的交点(K≠D).设∠BAD、∠ABC、∠BCD、∠ADC的外角平分线分别为l A、l B、l C、l D,l A和l B、l B和l C、l C和l D、l D和l A分别交于点G、H、I、J.△CDF的外接圆中,弧DF(不含C)的中点为Q,直线EH与△AED的外接圆交于另一点M.设GJ中垂线与IH中垂线(不重合)交于点P.证明:P、M、Q、K四点共圆.25、设D是△ABC外接圆⊙O上任意一点,过D作⊙O的切线l.证明:l关于△ABC三边对称的直线围成的三角形的外接圆与⊙O相切.26、设O为△ABC内一点,O在BC、CA、AB上的射影分别为U、V、W.X、Y、Z分别在BC、CA、AB上,X′、Y′、Z′分别是X关于U、Y关于V,Z关于W的对称点,点X、Y、Z关于△ABC的密克点为S,点X′、Y′、Z′关于△ABC的密克点为T.证明:OS=OT.B CX'U27、点D、E、F分别在△ABC的边AB、BC、CA上,满足AD+AF=BC、BD+BE=AC、CE+CF=AB. △ADF、△BDE、△CEF的外接圆与△ABC外接圆的另一个交点分别为A1、B1、C1,P是D、E、F关于△ABC的密克点,证明:P为△A1B1C1的垂心.128、设AA′、BB′、CC′是锐角△ABC的外接圆的三条直径,P为△ABC内任意一点,点P在BC、CA、AB上的射影分别是D、E、F,X、Y、Z分别是A′关于D、B′关于E,C′关于F的对称点.证明:△XYZ∽△ABC.29、设H是锐角△ABC的外接圆的垂心,P是外接圆弧BC上一点,连接PH交弧AC于M,弧AB上一点K满足直线KM平行于点P关于△ABC的西姆松线,设Q为外接圆上一点满足30、设△ABC的内切圆⊙I分别切BC、CA、AB于点D、E、F,延长EI交DF于G,BE、CF交⊙I于另外的点X、Y.设J为△AEF外接圆的另一个交点,△XJI外接圆与⊙I的另一个交点为S,T在⊙I上满足TS⊥AI,连接YT、XS交于P,直线DP与⊙I的另一个交点为Q.证明:KQ是⊙I的直径.C31、在△ABC中,内切圆⊙I分别切BC、CA、AB于点D、E、F,M、N分别是AB、AC的中点,EF、MN交于S,DS与⊙I的另一个交点为J.证明:J在△ABC的九点圆上.B C32、过△ABC内心I任作一直线l,内切圆分别切BC、CA、AB于点X、Y、Z,边BC、CA、AB的中点分别为D、E、F,直线l分别交△BIC外接圆、△CIA外接圆、△AIB外接圆于另一点D′、E′、F′,过点X、Y、Z分别作平行于DD′、EE′、FF′的直线l1、l2、l3.证明:直线l1、l2、l3交于一点.33、已知△ABC的外接圆为⊙O,A′为点A在⊙O上的对径点.作等边△BCD,使得A、D位的于BC的异侧,过点A′作A′D的垂线,分别与AC、AB交于E、F两点.以EF为底,作底角为π6等腰△ETF,并使得A、T位于BC的异侧.证明:AT经过△ABC的九点圆圆心.ED34、设△ABC的内切圆⊙I与边BC、CA、AB分别切于点D、E、F,记⊙I B、⊙I C分别为△ABC的顶点B、C所对的旁切圆,P、Q分别为I B E,I C F的中点,若DE、DF与I B I C交于点K、J,EJ 与FK交于点M,PE与△PAC的外接圆交于另一点X,QF与△QAB的外接圆交于另一点Y.证明:BY、CX、AM三线共点.35、已知凸四边形ABCD内两动点P、Q满足∠APB=∠AQB=∠CPD=∠CQD.证明:动直线PQ要么均经过一个定点,要么相互平行.36、在凸四边形ABCD中,∠ABC=∠ADC<π,∠ABC、∠ADC的平分线交于点P,并分2别与AC交于点E、F,M为AC的中点,BM、DM与△BDP的外接圆分别交于另一点X、Y,EX与PY交于点Q.证明:AC⊥PQ.B37、凸六边形A1A2A3A4A5A6满足A1A2=A3A4=A5A6,A2A3=A4A5=A6A1,点X、Y在38、已知凸四边形ABCD内接于⊙O,⊙I切AC、BD及⊙O,E为弧BC的中点,AE与BD相交于点M,DE与AC相交于点N.证明:△EMN外接圆与⊙I相切.39、锐角△ABC 中BC >AC >AB ,I 、O 、H 分别为其内心、外心、垂心,D 、E 分别在BC 、AC 上使AE =BD ,CD +CE =AB .记K 为BE 与AD 交点,证明:KH =2IO .ABC40、在锐角△ABC中,AB>AC,设Γ为其外接圆,H为垂心,F为由顶点A处所引高的垂足,M为边BC的中点.Q、K为圆Γ上的点,使得∠HQA=∠HKQ=π.若点A、B、C、K、Q互2不相同,且按此顺序排列在Γ上,证明:△KQH的外接圆与△FKM的外接圆相切.41、设△ABC内接于⊙O,过A作⊙O的切线交BC于T,G为△ABC的重心,直线TG分别交AB、AC于E、F,AG交⊙O于K,证明:AK平分∠EKF.K42、在凸四边形ABCD中,AB≠BC,ω1和ω2分别是△ABC和△ADC的内切圆.已知存在一个圆ω与射线BA相切(切点不在线段BA上),与射线BC相切(切点不在线段BC上),且与直线AD和直线CD都相切.证明:圆ω1和ω2的两条外公切线的交点在圆ω上.43、P为△ABC内一点,L、M、N分别为边BC、CA、AB的中点,且PL∶PM∶PN=BC∶CA∶AB.延长AP、BP、CP分别交△ABC的外接圆于点D、E、F.证明:△APF、△APE、△BPF、△BPD、△CPD、△CPE的外接圆圆心六点共圆.B44、给定△ABC,求线段BC上满足下列条件的所有点P:如果X、Y是直线PA与△PAB、△PAC外接圆的两条外公切线的交点,则(PAXY )2+PB∙PCAB∙AC=1.45、在凸四边形ABCD中,∠ABC=∠CDA=π2,H是A在BD上的射影,边AB上的S和边AD上的T使H在△SCT内部,∠CHS−∠CSB=π2,∠THC−∠DTC=π2,证明:直线BD和△TSH的外接圆相切.CD46、在△ABC中,⊙O、⊙I分别为其外接圆与内切圆,⊙I与BC切于点D,M为ID中点,A0与A 关于点O对称,直线A0M交⊙O于异于点A0的一点X,证明:△ADX的外接圆与直线BC相切.47、已知P 是凸四边形ABCD 的边AB 上的一点,ω是△CPD 的内切圆,I 为其圆心,若ω分别与△APD 以及△CPB 的内切圆切于点K 和L ,AC 与BD 交于点E ,AK 、BL 交于点F .证明:E 、I 、F 共线.BAD48、在锐角△ABC中,ω、Ω、R分别表示其内切圆、外接圆及外接圆的半径.圆ωA与Ω内切于点A且与ω外切;圆ΩA与Ω内切于点A且与ω内切.设P A和Q A分别是ωA和ΩA的圆心.同样定义P B和Q B、P C和Q C.证明:8P A Q A∙P B Q B∙P C Q C≤R349、已知△ABC的垂心为H,外心为O,设A、B、C关于BC、CA、AB的对称点分别为D、E、F.证明:D、E、F共线当且仅当OH=2R,其中R为△ABC外接圆半径.FCO50、设∠XAY是一个固定的角,B、C分别是射线AX、AY上的动点,∠XAY内有一动点P满足PA、PB、PC的长度都保持不变.求△ABC面积的最小值.。
平面几何100题及答案(前80题)
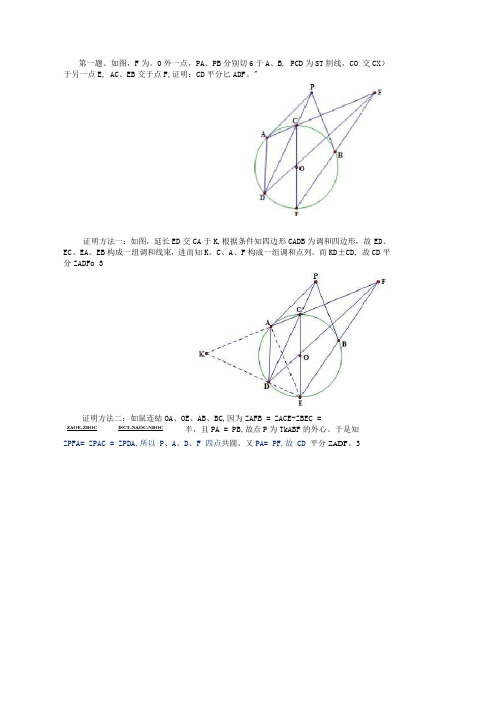
第一题、如图,F为。
0外一点,PA、PB分别切6于A、B, PCD为ST割线,CO 交CX)于另一点E, AC、EB交于点F,证明:CD平分匕ADF。
"证明方法一:如图,延长ED交CA于K,根据条件知四边形CADB为调和四边形,故ED、EC、EA、EB构成一组调和线束,进而知K、C、A、F构成一组调和点列。
而KD±CD, 故CD平分ZADFo 3证明方法二:如鼠连結OA、OE、AB、BC,因为ZAFB = ZACE-ZBEC =ZAOE-ZBOC ISCT-NAOC-NBOC 半,且PA = PB,故点P为TkABF的外心。
于是知ZPFA= ZPAC = ZPDA,所以P、A、D、F 四点共圆。
又PA= PF,故CD 平分Z A DF。
3第二题、如图,AB为©0直径,C、D为O。
上两点,且在AB同侧,。
在C、D两处的切城交于点E, BC、AD交于点F, EF交AB于证明:E、C、页、D四点共圆。
“证明:如图,延长白C、BD交于点K,则BC1AK, AD丄BK,从而知F^)AKAB的垂心。
又在圆内接六边形CCADDB中使用帕斯卡定理,知K、E、F三点共线,从而KM丄卽于価。
于是知匕CMF = ZCAF= ZCDE,所以E、C、页、D四点共圆。
K第三题、如图,AB为。
直径,C、D为伽上两点'且在AB同侧,O0在C. D两处的切线交于点E, BC、AD交于点F, EB交0。
于点G,证明;ZCEF = 2/AGF。
“证明:如图,根据条件知匕CF D =典牌=(脸-®;(i对-命)=Z CAB + / DBA = ZECF + ZEDF;且EC = ED;故点E 为△CED 外心。
于是知/EFC = ZECF = ZCAB = ZCGE,敌E、C、F、G四点共圆。
所以“ZCGF = ZCEF = 2(90° - ZECF)= 2(90° - ZCAB)= 2ZABC 二2ZAGC " 0lWZAGF = —=—,即得ZCEF = 2ZAGFo,2 2第四題、如图,AB为直径,P为AB延长线上一点,PC切于C,点C关于朋的对称点为点D, CE1AD于E, F为CE中点,AF交于K,求证:AP为ZXPCK外扬圆的切线。
高考数学平面解析几何专项训练(100题-含答案)

高考数学平面解析几何专项训练(100题-含答案)1.在平面直角坐标系xOy 中,已知点12(1,0),(1,0)F F -,点M 满足12MF MF +=记点M 的轨迹为曲线C .(1)求曲线C 的方程;(2)点T 在直线2x =上,过T 的两条直线分别交C 于,A B 两点和,P Q 两点,且||||||||TA TB TP TQ ⋅=⋅,求直线AB 的斜率与直线PQ 的斜率之和.【答案】(1)2212x y +=(2)0【解析】【分析】(1)根据122MF MF +=,利用椭圆的定义求解;(2)设()2,T m ,直线AB 的参数方程为()2cos ,sin x t y m t θθθ=+⎧⎨=+⎩为参数,与椭圆方程联立,利用参数的几何意义求解.(1)解:因为122MF MF +=,所以点M 的轨迹是以12(1,0),(1,0)F F -为焦点的椭圆,则21,1a c b ===,所以椭圆的方程是2212x y +=;(2)设()2,T m ,直线AB 的参数方程为()2cos ,sin x t y m t θθθ=+⎧⎨=+⎩为参数,与椭圆方程联立()()2222cos 2sin 4cos 4sin 420t m t m θθθθ+++++=,由参数的几何意义知:12,TA t TB t ==,则22122224242cos 2sin 2cos m m t t θθθ++⋅=-=-+-,设直线PQ 的参数方程为:()2cos ,sin x y m λαλλα=+⎧⎨=+⎩为参数,则12,TP TQ λλ==,则22122224242cos 2sin 2cos m m λλααα++⋅=-=-+-,由题意得:222242422cos 2cos m m θα++-=---,即22cos cos θα=,因为αθ≠,所以cos cos θα=-,因为0,0θπαπ<<<<,所以θαπ+=,所以直线AB 的斜率tan θ与直线PQ 的斜率tan α之和为0.2.设n S 是数列{}n a 的前n 项和,13a =,点(),N n S n n n *⎛⎫∈ ⎪⎝⎭在斜率为1的直线上.(1)求数列{}n a 的通项公式;(2)求数列12n n a +⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】(1)21n a n =+(2)152522n n n T ++=-【解析】【分析】(1)根据斜率公式可得出()222n S n n n =+≥,可知13S =满足()222n S n n n =+≥,可得出22n S n n =+,再利用11,1,2n n n S n a S S n -=⎧=⎨-≥⎩可求得数列{}n a 的通项公式;(2)求得1212n n n c ++=,利用错位相减法可求得n T .(1)解:由13a =,点,n S n n ⎛⎫ ⎪⎝⎭在斜率为1的直线上,知1111n S S n n -=-,即()222n S n n n =+≥.当1n =时,113S a ==也符合上式,故22n S n n =+.当2n ≥时,()()221212121n n n a S S n n n n n -⎡⎤=-=+--+-=+⎣⎦;13a =也满足上式,故21n a n =+.(2)解:112122n n n n a n c +++==.则2341357212222n n n T ++=++++ ,所以,3412135212122222n n n n n T ++-+=++++ ,上式-下式得1232211113111213214212422224212n n n n n n n T -++⎛⎫- ⎪++⎛⎫⎝⎭=++++-=+- ⎝⎭- 252542n n ++=-,因此,152522n n n T ++=-.3.椭圆2222:1(0)x y C a b a b +=>>的离心率为3,且过点(3,1).(1)求椭圆C 的方程;(2)A ,B ,P 三点在椭圆C 上,O 为原点,设直线,OA OB 的斜率分别是12,k k ,且1213k k ⋅=-,若OP OA OB λμ=+,证明:221λμ+=.【答案】(1)221124x y +=(2)证明见解析【解析】【分析】(1)由条件可得c a22911a b +=,222c b a +=,解出即可;(2)设()()()112200,,,,,A x y B x y P x y ,由条件可得012012x x x y y y λμλμ=+⎧⎨=+⎩,12123x x y y =-,然后将01212x x x y y y λμλμ=+⎧⎨=+⎩代入椭圆方程可得2222221122121221124124124x y x y x x y y λμλμ⎛⎫⎛⎫⎛⎫+++++= ⎪ ⎪⎝⎭⎝⎭⎝⎭,然后可得答案.(1)因为ca=22911a b +=,222c b a +=所以可解得2a b ⎧=⎪⎨=⎪⎩所以椭圆C 的方程221124x y +=.(2)设()()()112200,,,,,A x y B x y P x yOP OA OB λμ=+ ,012012x x x y y y λμλμ=+⎧∴⎨=+⎩()()222212120011124124x x y y x y λμλμ+++=∴+= 即2222221122121221124124124x y x y x x y y λμλμ⎛⎫⎛⎫⎛⎫+++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2222112211124124x y x y +=+= ,,即22121221124x x y y λμλμ⎛⎫+++= ⎪⎝⎭又1212121133y y k k x x ⋅=-∴=- ,即12123x x y y =-,221λμ∴+=4.已知椭圆()2222:10x y C a b a b+=>>,A 、B 分别为椭圆C 的右顶点、上顶点,F 为椭圆C的右焦点,椭圆C 的离心率为12,ABF 的面积为32.(1)求椭圆C 的标准方程;(2)点P 为椭圆C 上的动点(不是顶点),点P 与点M ,N 分别关于原点、y 轴对称,连接MN 与x 轴交于点E ,并延长PE 交椭圆C 于点Q ,则直线MP 的斜率与直线MQ 的斜率之积是否为定值?若是,求出该定值;若不是,请说明理由.【答案】(1)22143x y +=(2)是定值,定值为32-【解析】【分析】(1)根据椭圆的离心率可得到a,b,c 的关系,再结合ABF 的面积可得到()a c b -=,由此解得a,b ,可得答案.(2)设直线方程,并联立椭圆方程,得到根与系数的关系式,结合直线MP 的斜率与直线MQ 的斜率之积,代入化简可得答案.(1)由题意得12c a =,则2a c =,b =.ABF 的面积为()1322a cb -=,则()a c b -将2a c =,b =代入上式,得1c =,则2a =,b =,故椭圆C 的标准方程为22143x y +=.(2)由题意可知直线PQ 的斜率一定存在,设直线PQ 的方程为y kx m =+,设()11,P x y ,()22,Q x y ,则()11,M x y --,()11,N x y -,()1,0E x -,联立方程22143x y y kx m ⎧+=⎪⎨⎪=+⎩,得()2223484120k x kmx m +++-=,∴122834kmx x k +=-+,∴()12122286223434km m y y k x x m k m k k ⎛⎫+=++=-+= ⎪++⎝⎭,∴21212263348434MQmy y k k km x x kk ++===-+-+,112PEPQ y k k k x ===,∵11112222MP PE y yk k k x x ====,∴33242MP MQ k k k k ⋅=-⨯=-∴MP MQ k k ⋅为定值32-.【点睛】本题考查了椭圆方程的求法以及直线和椭圆的位置关系,综合考查了学生分析问题,解决问题以及计算方面的能力和综合素养,解答的关键是理清解决问题的思路,并能正确地进行计算.5.已知圆M 过点()1,0,且与直线1x =-相切.(1)求圆心M 的轨迹C 的方程;(2)过点()2,0P 作直线l 交轨迹C 于A 、B 两点,点A 关于x 轴的对称点为A '.问A B '是否经过定点,若经过定点,求出定点坐标;若不经过,请说明理由.【答案】(1)24y x =(2)()2,0-【解析】【分析】(1)根据抛物线的定义计算可得;(2)设直线l 的方程为2x ty =+,()11,A x y 、()22,B x y ,则()11,A x y '-,联立直线与抛物线方程,消元、列出韦达定理,再表示出直线A B '的方程,将12y y +、12y y 代入整理即可得解;(1)解:由题意知动点M 的轨迹C 是以(0,0)O 为顶点,()1,0为焦点,1x =-为准线的抛物线,所以动圆圆心M 的轨迹方程为:24y x =;(2)解:设直线l 的方程为2x ty =+,()11,A x y 、()22,B x y 不妨令21y y >,则()11,A x y '-,联立直线l 与抛物线方程得224x ty y x =+⎧⎨=⎩消去x 得2480y ty --=,则124y y t +=、128y y =-,则直线A B '的方程为()()211121y y y y x x x x +--=--,即()()21212121x x y x y y y x y x -+=+-,则()()()()2121212122ty ty y ty y y y x y ty -++=+-+,()()()2121211222t y y y y y x ty y y y -=+--+,即()()21211222y y y x ty y y y =+--+,所以()42824y tx t t ⋅=-⨯--⨯,即()2y t x =+,令200x y +=⎧⎨=⎩解得20x y =-⎧⎨=⎩,所以直线A B '恒过定点()2,0-;6.已知1F ,2F 是椭圆C :()222104x yb b+=>的左、右焦点,过1F 的直线与C 交于A ,B两点,且22::3:4:5AF AB BF =.(1)求C 的离心率;(2)设M ,N 分别为C 的左、右顶点,点P 在C 上(P 不与M ,N 重合),证明:MPN MAN ∠≤∠.【答案】(2)见解析【解析】【分析】(1)由题意设223,4,5AF m AB m BF m ===,由勾股定理的逆定理可得290BAF ∠=︒,再根据椭圆的定义可求出m 的值,从而可求出12,AF AF 的值,则可得点A 是椭圆短轴的一个端点,进而可求出离心率,(2)由椭圆的对称性,不妨设00(,)P x y,0y ∈,,PMN PNM αβ=∠=∠,则可得0000tan ,tan 22y y x x αβ==+-,然后求出tan tan αβ+,tan tan αβ,再利用正切的两角和公式可得02tan()y αβ+=,由正切函数可求出αβ+的最小值,从而可求出()MPN παβ∠=-+的最大值,进而可证得结论(1)由()222104x y b b+=>,得24a =,得2a =,由题意设223,4,5AF m AB m BF m ===,则22222AF AB BF +=,所以290BAF ∠=︒,因为223451248AF AB BF m m m m a ++=++===,所以23m =,所以22AF =,所以122422AF a AF =-=-=,所以12AF F △为等腰直角三角形,所以点A 是椭圆短轴的一个端点,所以b c =,因为222224b c b a +===,得b c =所以椭圆的离心率为2c e a ==(2)由(1)可得椭圆方程为22142x y +=,则(2,0),(2,0)M N -,因为点A是椭圆短轴的一个端点,所以不妨设A ,由椭圆的对称性,不妨设00(,)P x y,0y ∈,,PMN PNM αβ=∠=∠,则0000tan ,tan 22y y x x αβ==+-,2200142x y +=,所以2200002200001tan tan 22422y y y y x x x y αβ⋅=⋅===+--,00002200000442tan tan 2242y y y y x x x y y αβ+=+===+--,所以0tan tan 4tan()1tan tan y αβαβαβ++==-,所以当0y =tan()αβ+取得最小值由(1)可知290BAF ∠=︒,所以()0,2παβ⎛⎫+∈ ⎪⎝⎭,所以当tan()αβ+取得最小值时,αβ+取得最小值,即点P 与点A 重合时,αβ+取得最小值,此时()MPN παβ∠=-+取得最大,所以MPN MAN∠≤∠7.已知椭圆()2222:10x y C a b a b+=>>的长轴长为,且过点)P(1)求C 的方程:(2)设直线()0y kx m m =+>交y 轴于点M ,交C 于不同两点A ,B ,点N 与M 关于原点对称,BO AN ⊥,Q 为垂足.问:是否存在定点M ,使得·NQ NA 为定值?【答案】(1)221102x y +=(2)存在【解析】【分析】(1)利用待定系数法求方程;(2)联立方程组,结合韦达定理可得直线恒过定点,进而求解.(1)依题意知2a =a =所以C 的方程可化为222110x y b+=,将点)P代入C 得251110b +=,解得22b =,所以椭圆方程为221102x y +=;(2)设点()11,A x y ,()22,B x y ,联立221102x y y kx m ⎧+=⎪⎨⎪=+⎩得,()22215105100k x kmx m +++-=,()()()222104155100km k m ∆=-+->,解得22210m k <+,1221015km x x k -+=+,212251015m x x k -=+,注意到Q ,N ,A 三点共线,NQ NA NQ NA ⋅=⋅,又()NQ NA NB BQ NA NB NA ⋅=+⋅=⋅()()()()1212121222x x y m y m x x kx m kx m =+++=+++()()()()222222212122215102012441515k m k mkx xmk x x mm kk+-=++++=-+++()222221510510415k m m m k--+-=++当()2215105510m m --=-,解得1m =±,因为0m >,所以1m =,此时1NQ NA ⋅=-,满足0∆>,故存在定点()0,1M ,使得1NQ NA ⋅=-等于定值1.【点睛】解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.8.已知椭圆C :22221(0)x y a b a b +=>>,4a M b ⎛⎫ ⎪⎝⎭为焦点是22y x =的抛物线上一点,H 为直线y a =-上任一点,A ,B 分别为椭圆C 的上,下顶点,且A ,B ,H 三点的连线可以构成三角形.(1)求椭圆C 的方程;(2)直线HA ,HB 与椭圆C 的另一交点分别交于点D ,E ,求证:直线DE 过定点.【答案】(1)2214x y +=(2)证明见解析【解析】【分析】(1)由椭圆的离心率求出,a c 的关系式,再由,4a M b ⎛⎫⎪⎝⎭为抛物线22=y x 上的点,结合222a b c =+,即可求出椭圆C 的方程.(2)设点()(),20H m m -≠,求得HA ,HB 的方程,与椭圆联立求得,D E 坐标,写出直线DE 的方程,即可求出DE 恒过的定点.(1)由题意知,222224c aa b a b c⎧=⎪⎪⎪=⨯⎨⎪=+⎪⎪⎩,解得21a b c ⎧=⎪=⎨⎪=⎩,∴椭圆C 的方程为2214x y +=.(2)设点()(),20H m m -≠,易知()0,1A ,()0,1B -,∴直线HA 的方程为31y x m =-+,直线HB 的方程为11y x m=--.联立223114y x m x y ⎧=-+⎪⎪⎨⎪+=⎪⎩,得22362410x x m m ⎛⎫+-= ⎪⎝⎭,∴22436D m x m =+,223636D m y m -=+,同理可得284E m x m -=+,2244E m y m -=+,∴直线DE 的斜率为21216m k m-=,∴直线DE 的方程为222241284164m m m y x m m m --⎛⎫-=+ ⎪++⎝⎭,即2121162m y x m -=-,∴直线DE 过定点10,2⎛⎫- ⎪⎝⎭.9.已知点(1,2)M -在抛物线2:2(0)E y px p =>上.(1)求抛物线E 的方程;(2)直线12,l l 都过点12(2,0),,l l 的斜率之积为1-,且12,l l 分别与抛物线E 相交于点A ,C 和点B ,D ,设M 是AC 的中点,N 是BD 的中点,求证:直线MN 恒过定点.【答案】(1)24y x =(2)证明见解析【解析】【分析】(1)将点坐标代入求解抛物线方程;(2)设出直线方程,表达出,M N 的坐标,求出直线MN 的斜率,利用直线斜率之积为-1,求出直线MN 恒过的定点,从而证明出结论.(1)∵点(1,2)M -在抛物线2:2E y px =上,∴2(2)2p -=,∴解得:2p =,∴抛物线E 的方程为:24y x =.(2)由12,l l 分别与E 相交于点A ,C 和点B ,D ,且由条件知:两直线的斜率存在且不为零.∴设1122:2,:2l x m y l x m y =+=+由214,2y x x m y ⎧=⎨=+⎩得:21480y m y --=设()()1122,,,A x y C x y ,则1214y y m +=,∴12M y m =,又2122M x m =+,即()21122,2M m m +同理可得:()22222,2N m m +∴()()212212212212222MN m m k m m m m -==++-+,∴()211121:222MN y m x m m m -=--+即MN :()1212121y x m m m m =--⎡⎤⎣⎦+,∵12,l l 的斜率之积为1-,∴12111m m ⋅=-,即121m m =-,∴121:(4)MN y x m m =-+,即直线MN 过定点(4,0).10.已知抛物线()20x ay a =>,过点0,2a M ⎛⎫ ⎪⎝⎭作两条互相垂直的直线12,l l ,设12,l l 分别与抛物线相交于,A B 及,C D 两点,当A 点的横坐标为2时,抛物线在点A 处的切线斜率为1.(1)求抛物线的方程;(2)设线段,AB CD 的中点分别为,E F ,O 为坐标原点,求证直线EF 过定点.【答案】(1)24x y =;(2)证明见解析.【解析】【分析】(1)结合导数知识,利用切线斜率构造方程可得a ,由此可得抛物线方程;(2)将直线AB 方程代入抛物线方程中,结合韦达定理可确定中点坐标,同理可得CD中点坐标,利用直线方程两点式可得直线EF 方程,化简可知其过定点()0,4.(1)由2x ay =得:21y ax =,则2y x a '=,241x y a=∴==',解得:4a =,∴抛物线方程为:24x y =;(2)由题意知:直线12,l l 的斜率都存在且都不为零,由(1)知:()0,2M ,设直线:2AB y kx =+,代入24x y =得:2480x kx --=,设()11,A x y ,()22,B x y ,则124x x k +=,128x x =-,()21212444y y k x x k ∴+=++=+,AB ∴中点()22,22E k k +;12l l ⊥ ,1:2CD y x k ∴=-+,同理可得:CD 中点222,2F k k ⎛⎫-+ ⎪⎝⎭;EF ∴的方程为:()()222222222222k k y k x k k k ⎛⎫+-+ ⎪⎝⎭-+=-+,化简整理得:14y k x k ⎛⎫=-+ ⎪⎝⎭,则当0x =时,4y =,∴直线EF 恒过定点()0,4.【点睛】思路点睛:本题考查直线与抛物线综合应用中的直线过定点问题的求解,求解此类问题的基本思路如下:①假设直线方程,与抛物线方程联立,整理为关于x 或y 的一元二次方程的形式;②利用0∆>求得变量的取值范围,得到韦达定理的形式;③利用韦达定理表示出已知中的等量关系,代入韦达定理可整理得到变量间的关系,从而化简直线方程;④根据直线过定点的求解方法可求得结果.11.在直角坐标系xOy 中,曲线:C 221x y +=经过伸缩变换x xy '='=⎧⎪⎨⎪⎩后的曲线为1C ,以x 轴正半轴为级轴,建立极坐标系.曲线2C的极坐标方程为sin 4πρθ⎛⎫+= ⎪⎝⎭(1)写出1C 的普通方程和2C 的直角坐标方程;(2)若1C 上的一点P 到2C 的距离的最大,求距离的最大值及P 点的坐标.【答案】(1)1C :2213y x +=,2C :40x y +-=;(2)max d =,1322P ⎛⎫-- ⎪⎝⎭,.【解析】【分析】()1直接利用转换关系,把参数方程,直角坐标方程和极坐标方程之间进行转换;()2利用三角函数关系式的变换和点到直线的距离公式的应用求出结果.(1)解:由伸缩变换x xy '='=⎧⎪⎨⎪⎩得,代入曲线:C 221x y +=得:1C 的普通方程为2213y x +=,由极坐标方程sin 4πρθ⎛⎫+= ⎪⎝⎭sin y ρθ=,cos x ρθ=可得:2C 的直角坐标方程为40x y +-=.(2)解:直线2C 的普通方程为40x y +-=,设1C上的为点()cos P θθ,到2C 的距离为d =当且仅当()223k k Z πθπ=-+∈时,取得max d =,又因为1cos 23y 2x θθ⎧==-⎪⎪⎨⎪==-⎪⎩,即点P 的坐标为1322⎛⎫-- ⎪⎝⎭.12.已知椭圆C :2222+x y a b=1(a >b >0)经过点A (0,1),且右焦点为F (1,0).(1)求C 的标准方程;(2)过点(0,12)的直线l 与椭圆C 交于两个不同的点P .Q ,直线AP 与x 轴交于点M ,直线AQ 与x 轴交于点N .证明:以MN 为直径的圆过y 轴上的定点.【答案】(1)2212x y +=(2)证明见解析【解析】【分析】(1)由已知得,c b ,再求得a ,即得椭圆方程;(2)由题意直线l 斜率存在,可设直线1:2l y kx =+,设()()1122,,,P x y Q x y ,直线方程代入椭圆方程应用韦达定理得1212,x x x x +,由直线,AP AQ 方程求出,M N 坐标,求出以MN 为直径的圆的方程,然后代入1212,x x x x +求得圆方程的常数项,从而可得y 的定点坐标.(1)由题意可得1,1c b ==从而22a =.所以椭圆的标准方程为2212x y +=.(2)证明:由题意直线l 斜率存在,可设直线1:2l y kx =+,设()()1122,,,P x y Q x y ,将直线l 代入椭圆方程得()2242430k x kx ++-=,所以12122243,,4242k x x x x k k --+==++,直线AP 的方程为1111y y x x -=+,直线AQ 的方程为2211y y x x -=+.可得1212,0,,011x x M N y y ⎛⎫⎛⎫--⎪ ⎪--⎝⎭⎝⎭,以MN 为直径的圆方程为,21212011x x x x y y y ⎛⎫⎛⎫+++= ⎪⎪--⎝⎭⎝⎭,即()()221212121201111x x x x x y x y y y y ⎛⎫++++= ⎪----⎝⎭.①因为()()()1212122121212124111142122x x x x x x y y k x x k x x kx kx ==---++⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭22212612842k k k -==--+++.所以在①中令0x =,得26y =,即以MN 为直径的圆过y轴上的定点(0,,13.已知抛物线C :()220y px p =>,过点()2,0R 作x 轴的垂线交抛物线C 于G ,H 两点,且OG OH ⊥(O 为坐标原点).(1)求p ;(2)过()2,1Q 任意作一条不与x 轴垂直的直线交抛物线C 于A ,B 两点,直线AR 交抛物线C 于不同于点A 的另一点M ,直线BR 交抛物线C 于不同于点B 的另一点N .求证:直线MN 过定点.【答案】(1)1p =(2)证明见解析【解析】【分析】(1)由题意知2RG OR ==,不妨设()2,2G ,代入抛物线方程中可求出p 的值,(2)设211,2y A y ⎛⎫ ⎪⎝⎭,222,2y B y ⎛⎫ ⎪⎝⎭,233,2y M y ⎛⎫ ⎪⎝⎭,244,2y N y ⎛⎫⎪⎝⎭,则可表示出直线AB ,AM ,BN 的方程,再由直线AB 过()2,1Q 及直线AM ,BN 过()2,0R 可得()121240y y y y -++=,13244y y y y ==-,再表示出直线MN 的方程,结合前面的式子化简可得结论(1)由题意知,2RG OR ==.不妨设()2,2G ,代入抛物线C 的方程,得44p =解得1p =.(2)由(1)知,抛物线C 的方程为22y x =.设211,2y A y ⎛⎫ ⎪⎝⎭,222,2y B y ⎛⎫ ⎪⎝⎭,233,2y M y ⎛⎫ ⎪⎝⎭,244,2y N y ⎛⎫ ⎪⎝⎭,则直线AB 的斜率为12221212222AB y y k y y y y -==+-.所以直线AB 的方程为2111222y y x y y y ⎛⎫=-+ ⎪+⎝⎭,即()121220x y y y y y -++=.同理直线AM ,BN ,MN 的方程分别为()131320x y y y y y -++=,()242420x y y y y y -++=,()343420x y y y y y -++=,由直线AB 过()2,1Q 及直线AM ,BN 过()2,0R 可得()121240y y y y -++=,13244y y y y ==-.又直线MN 的方程为()343420x y y y y y -++=,即1212441620x y y y y y ⎛⎫+++= ⎪⎝⎭.所以直线MN 的方程为()1212280y y x y y y +++=.把()121240y y y y -++=代入()1212280y y x y y y +++=,得()12122480y y x y y y +++=,()122)880(y y x y y +++=,所以由20x y +=,880y +=可得2x =,1y =-.所以直线MN 过定点()2,1-.14.已知抛物线C :y 2=4x 的焦点为F ,过点F 的直线l 与抛物线C 交于P ,A 两点,且PF λFA = .(1)若λ=4,求直线l 的方程;(2)设点E (a ,0),直线PE 与抛物线C 的另一个交点为B ,且PE EB μ=.若λ=4μ,求a的值.【答案】(1)4340x y --=或4340x y +-=(2)4【解析】【分析】(1)由4PF FA =得014y y =-,设直线l :1x my =+,与抛物线C :24y x =联立,结合韦达定理,即得解;(2)由PF λFA = 得01y y λ=-,结合014y y =-,可得204y λ=,再由PE EB μ= 得02y y μ=-,设直线PB :x ny a =+,与抛物线C :24y x =联立由韦达定理可得024y y a =-,故204y aμ=,又4λμ=,代入运算即得解(1)易知焦点F (1,0),设P (0x ,0y ),A (1x ,1y )由4PF FA =得014y y =-设直线l :1x my =+,与抛物线C :24y x =联立得2440y my --=,其中216160m ∆=+>,所以014y y =-由①②可得0141y y =⎧⎨=-⎩或0141y y =-⎧⎨=⎩又014y y m +=,所以34m =或34m =-所以直线l 的方程为314x y =+或314x y =-+.化简得4340x y --=或4340x y +-=(2)由PF λFA =得01y y λ=-又014y y =-可得204y λ=设点B (2x ,2y ),由PE EB μ= 得02y y μ=-设直线PB :x ny a =+,与抛物线C :24y x =联立得2440y ny a --=.所以216()0n a ∆=+>,024y y a=-故204y aμ=又4λμ=,所以2200444y y a=⋅,考虑到点P 异于原点,所以00y ≠,解得4a =此时2216()16(4)0n a n ∆=+=+>所以a 的值为415.平面直角坐标系xOy 中,双曲线22:136x y C -=的右焦点为F ,T 为直线:1l x =上一点,过F 作TF 的垂线分别交C 的左、右支于P 、Q 两点,交l 于点A .(1)证明:直线OT 平分线段PQ ;(2)若3PA QF =,求2TF 的值.【答案】(1)证明见解析(2)12+【解析】【分析】(1)设直线PQ 的方程为3x ty =+,设点()11,P x y 、()22,Q x y ,将直线PQ 的方程与双曲线的方程联立,列出韦达定理,求出线段PQ 的中点N 的坐标,计算得出ON OT k k =,证明出O 、T 、N 三点共线,即可证得结论成立;(2)由3PA QF =得3PA QF = ,可得出1238x x -+=,变形可得出()()12212184384x x x x x x ⎧++=⎪⎨+-=⎪⎩,两式相乘结合韦达定理可求得2t 的值,再利用两点间的距离公式可求得2TF 的值.(1)解:依题意,3F x ==,即()3,0F ,设()1,2T t ,则直线PQ 的方程为3x ty =+,由22326x ty x y =+⎧⎨-=⎩得()222112120t y ty -++=,设()11,P x y 、()22,Q x y ,则()222210Δ14448210t t t ⎧-≠⎪⎨=-->⎪⎩,故212t ≠,由韦达定理可得1221221t y y t +=--,1221221y y t =-,所以()121226621x x t y y t +=++=--,又直线PQ 分别交C 的左、右支于P 、Q 两点,所以()()()22121212122963339021t x x ty ty t y y t y y t +=++=+++=-<-,故212t >所以PQ 中点为2236,2121t N t t ⎛⎫-- ⎪--⎝⎭,所以2ON OT k t k ==,故O 、T 、N 三点共线,即直线OT 平分线段PQ .(2)解:依题意,由3PA QF =得3PA QF =,则()12133x x -=-,即1238x x -+=,所以()12284x x x ++=,①,()121384x x x +-=,②①×②得()()21212123166416x x x x x x +++-=,所以()22222366963166416212121t t t t+⨯-⨯-=-⨯---,解得28374t +=,或28374t -=(舍去),此时,224412t TF =+=+【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:(1)设直线方程,设交点坐标为()11,x y 、()22,x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,必要时计算∆;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x (或12y y +、12y y )的形式;(5)代入韦达定理求解.16.已知抛物线2:4E y x =,F 为其焦点,O 为原点,A ,B 是E 上位于x 轴两侧的不同两点,且5OA OB ⋅=.(1)求证:直线AB 恒过一定点;(2)在x 轴上求一定点C ,使F 到直线AC 和BC 的距离相等;(3)在(2)的条件下,当F 为ABC 的内心时,求ABC 重心的横坐标.【答案】(1)证明见解析(2)见解析(3)173【解析】【分析】(1)设直线AB 的方程为x my n =+,211(,)4y A y ,222(,)4y B y ,联立24x my n y x =+⎧⎨=⎩,消x 得:2440y my n --=,124y y m +=,124y y n =-,结合向量的数量积,转化求解直线AB 的方程,推出结果.(2)在x 轴上求一定点C ,使F 到直线AC 和BC 的距离相等即CF 平分ACB ∠,即直线AC 与直线BC 关于x 轴对称,根据斜率和为零,从而可得结果;(3)设11(,)A x y ,22(,)B x y ,直线AB 与x 轴交于N ,由题意可得32AC CF AN NF ==,坐标化,结合点在抛物线上可得点的坐标,从而得到结果.(1)设直线AB 的方程为x my n =+,211(,)4y A y ,222(,)4y B y ,联立24x my n y x=+⎧⎨=⎩,消x 得:2440y my n --=,则124y y m +=,124y y n =-,由5OA OB ⋅= 得:21212()516y y y y +=,所以:1220y y =-或124y y =(舍去),即4205n n -=-⇒=,所以直线AB 的方程为5x my =+,所以直线AB 过定点(5,0)P .(2)由(1)知,直线AB 过定点(5,0)P 可设直线AB 的方程为5x my =+,此时124y y m +=,1220y y =-,设x 轴上定点C 坐标为(,0)t ,要使F 到直线AC 和BC 的距离相等,则CF 平分ACB ∠,即直线AC 与直线BC 关于x 轴对称,故0AC BC k k +=,即21210y yx t x t+=--,∴()()21120y x t y x t -+-=,∴()()1212250my y t y y +-+=,∴()40450m m t -+-=对任意m 恒成立,∴510t -=,5t =-,故在x 轴上有一定点C (5,0)-,使F 到直线AC 和BC 的距离相等;(3)设11(,)A x y ,22(,)B x y ,直线AB 与x 轴交于N ,∵F 为ABC 的内心,∴32AC CF AN NF ==,32=,即2211126250x y x +-+=,又2114y x =,∴21122250x x -+=,同理22222250x x -+=,∴12,x x 是方程222250x x -+=的两个根,∴1222x x +=,∴三角形重心的横坐标为1251733x x +-=.17.已知椭圆C 的两个顶点分别为()2,0A -,()2,0B ,焦点在x (1)求椭圆C 的方程;(2)若直线()()10y k x k =-≠与x 轴交于点P ,与椭圆C 交于M ,N 两点,线段MN 的垂直平分线与x 轴交于Q ,求MN PQ的取值范围.【答案】(1)2214x y +=;(2)(4,【解析】【分析】(1)由顶点和离心率直接求,,a b c 即可;(2)先联立直线和椭圆方程,借助弦长公式表示出弦长MN ,再求出垂直平分线和Q 坐标,表示出PQ ,最后分离常数求取值范围即可.(1)由题意知2222,a c a a b c =⎧⎪⎪=⎨⎪=+⎪⎩可得1,2a b ==,故椭圆C 的方程为2214x y +=.(2)由()22114y k x x y ⎧=-⎪⎨+=⎪⎩,可得()2222418440k x k x k +-+-=,设()()1122,,,M x y N x y ,则22121222844,4141k k x x x x k k -+=⋅=++,()121222241k y y k x x k -+=+-=+,线段MN 的中点为2224,4141k k k k ⎛⎫- ⎪++⎝⎭,线段MN 的垂直平分线方程为22214()4141k k y x k k k --=--++,令0y =,得22341kx k =+,所以223,041k Q k ⎛⎫ ⎪+⎝⎭,又(1,0)P ,则22223114141k k PQ k k +=-=++,又12MN x x =-=所以2241141MN k k PQk +==++220,1331k k ≠∴<-<+ ,故MN PQ的取值范围为(4,.【点睛】(1)关键在于建立,,a b c 的关系式求解;(2)关键在于联立直线和椭圆方程,依次求出垂直平分线和弦长MN 、PQ ,转化成关于k 的代数式求范围即可.18.定义平面曲线的法线如下:经过平面曲线C 上一点M ,且与曲线C 在点M 处的切线垂直的直线称为曲线C 在点M 处的法线.设点()()000,0M x y y >为抛物线2:2(0)C y px p =>上一点.(1)求抛物线C 在点M 处的切线的方程(结果不含0x );(2)求抛物线C 在点M 处的法线被抛物线C 截得的弦长||AB 的最小值,并求此时点M 的坐标.【答案】(1)002y py x y =+(2);()p 【解析】【分析】(1)先化简求导确定切线斜率,再按照在点处的切线方程进行求解;(2)先联立法线和抛物线方程,借助弦长公式表示弦长,最后换元构造函数,求导确定最小值.(1)因为点()()000,0M x y y >在抛物线上方,所以由2:2(0)C y px p =>得y =py y'=,所以在点M 处的切线斜率0y y pk y y ='==,所求切线方程为000()py y x x y -=-,又202y x p=,故切线方程为2000()2y p y y x y p -=-,即002y p y x y =+.(2)点M 处的法线方程为2000()2y y y y x p p-=--,即220022y p p x y y p +=-+.联立抛物线2:2(0)C y px p =>,可得()2232000220y y p y y p y +-+=,可知0∆>,设()()1122,,,A x y B x y ,()2221212002,2p y y y y y p y +=-⋅=-+,所以322212202()y p AB y y y +⋅-=.令200t y =>,则3222()(0)t p AB t t +=>,令3222()()(0)t p f t t t +=>,1312222222223()()()(2)2()2t p t t p t p t p f t t t +⋅-++⋅-'=⨯=,所以()f t 在()20,2p 单调递减,在()22,p +∞单调递增,所以()2min ()2f t f p ==,即min AB =,此时点M的坐标为()p .【点睛】(1)关键在于化简出0y >时的抛物线方程,借助求导确定切线斜率;(2)写出法线方程,联立抛物线求弦长是通用解法,关键在于换元构造函数之后,借助导数求出最小值.19.已知点()11,0F -,()21,0F ,M 为圆22:4O x y +=上的动点,延长1F M 至N ,使得1MN MF =,1F N 的垂直平分线与2F N 交于点P ,记P 的轨迹为Γ.(1)求Γ的方程;(2)过2F 的直线l 与Γ交于,A B 两点,纵坐标不为0的点E 在直线4x =上,线段OE 分别与线段AB ,Γ交于,C D 两点,且2OD OC OE =⋅,证明:AC BC =.【答案】(1)22143x y +=;(2)证明见解析.【解析】【分析】(1)由线段垂直平分线和三角形中位线性质可证得12124PF PF F F +=>,可知P 点轨迹为椭圆,由此可得轨迹方程;(2)由已知可知24D C x x =;当l 斜率不存在时显然不成立;当l 斜率存在时,设l 方程,将其与椭圆方程联立,结合韦达定理可得AB 中点横坐标;设():0OE y k x k ''=≠,与直线l 和椭圆方程联立可求得34k k'=-,由此可整理得到C x ,与AB 中点横坐标相同,由此可得结论.(1)连接1,MO PF,PM 是1NF 的垂直平分线,1PF PN ∴=,1222PF PF PN PF NF ∴+=+=;,M O 分别为112,NF F F 中点,224NF MO ∴==,12124PF PF F F ∴+=>,P ∴点轨迹是以12,F F 为焦点,长轴长为4的椭圆,即2a =,1c =,23b ∴=,P ∴点轨迹Γ的方程为:22143x y +=;(2)2OD OC OE =⋅ ,即OD OE OC OD =,D EC Dx x x x ∴=,由题意知:0C x >,4E x =,24D C x x ∴=,①当直线l 斜率不存在时,即:1l x =,此时1C x =,2D x <,此时24D C x x =不成立;②当直线l 斜率存在时,设():1l y k x =-,()11,A x y ,()22,B x y ,由()221431x y y k x ⎧+=⎪⎨⎪=-⎩得:()22223484120k x k x k +-+-=,2122212283441234k x x k k x x k ⎧+=⎪⎪+∴⎨-⎪=⎪+⎩,AB ∴中点的横坐标为21224234x x k k +=+;设直线OE 的方程为:()0y k x k ''=≠,由()1y k x y k x ='=⎧⎨-⎩得:kx k k ='-,即C k x k k ='-;由22143y k xx y =⎧='⎪⎨+⎪⎩得:221234x k ='+,即221234D x k ='+;由24D C x x =得:212434k k k k =''+-,整理可得:34k k '=-,2122434324C x x kk x k k k+∴===++,C ∴为线段AB 的中点,AC BC ∴=.【点睛】关键点点睛:本题考查定义法求解轨迹方程、直线与椭圆综合应用问题;本题证明C 为AB 中点的关键是能够通过已知等式得到,C D 两点横坐标之间满足的等量关系,进而表示出AB 中点横坐标和C 点横坐标,证明二者相等即可.20.已知椭圆()2222:10x y E a b a b +=>>的左、右焦点分别为1F ,2F,离心率2e =,P为椭圆上一动点,12PF F △面积的最大值为2.(1)求椭圆E 的方程;(2)若C ,D 分别是椭圆E 长轴的左、右端点,动点M 满足MD CD ⊥,连结CM 交椭圆于点N ,O 为坐标原点.证明:OM ON ⋅为定值;(3)平面内到两定点距离之比是常数()1λλ≠的点的轨迹是圆.椭圆E 的短轴上端点为A ,点Q 在圆228x y +=上,求22QA QP PF +-的最小值.【答案】(1)22142x y +=;(2)见解析;4.【解析】【分析】(1)结合离心率和12PF F △面积的最大值列出关于,,a b c 的方程,解方程即可;(2)设直线CM 方程,写出点M 坐标,联立椭圆方程,求点N 坐标,通过向量数量积计算即可;(3)设点R 坐标,借助点Q 在圆228x y +=上,将2QA 转化成RA ,再借助椭圆定义将2PF 转化成14PF -,最后通过1,,R P F 三点共线求出最小值.(1)当P 为短轴端点时,12PF F △的面积最大,2bc =,222222,c a bc a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩解得2,a b c ===,故椭圆E 的方程为22142x y +=.(2)由(1)知,()2,0,(2,0)C D -,设直线():2CM y k x =+,11(,)N x y ,,(2,4)MD CD M k ⊥∴ ,联立221,42(2)x y y k x ⎧+=⎪⎨⎪=+⎩整理得()22222218840k x k x k +++-=,由21284221k x k --=+得2122421k x k -=+,1124(2)21ky k x k =+=+,222244(,)2121k k N k k -∴++,2222442442121k kOM ON k k k -⋅=⨯⨯++ ,故OM ON ⋅为定值4.(3)由题意(A ,设()(0,),,R m Q x y ,使2QA QR =,()()22222,4QR x y m QAx y +-==+,整理得222282833m m x y y --++=,又点Q 在圆228x y +=上,20,883m =∴⎨-⎪=⎪⎩解得m =,(0,R 由椭圆定义得124PF PF =-,2112(4)4QA QP PF QR QP PF QR QP PF +-=+--∴=++-,当1,,R P F三点共线时,(10,,(R F 22QA QP PF +-∴4.【点睛】(1)关键在于建立,,a b c 的方程;(2)关键在于设出直线方程,联立得出点N 坐标;(3)关键在于利用题目中给出的圆的定义将2QA 转化成RA ,再结合椭圆定义,将问题简化成共线问题.21.已知椭圆C :22221(0)x y a b a b+=>>的长轴长为4,点31,2⎛⎫ ⎪⎝⎭在椭圆C 上.(1)求椭圆C 的标准方程;(2)已知O 为坐标原点,P 为椭圆C 上的一个动点,过点E0)作OP 的平行线交椭圆C 于M ,N 两点,问:是否存在实数t (t >0),使得||,||,||EM t OP EN 构成等比数列?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)22143x y +=(2)存在,12t =【解析】【分析】(1)由题意可得2a =,再将点31,2⎛⎫ ⎪⎝⎭代入椭圆方程中可求出2b ,从而可求得椭圆的方程,(2)①当OP 的斜率存在时,设直线OP 的方程为y kx =,将直线方程代入椭圆方程中可求出22,x y ,则可得2OP ,设直线MN的方程为()()1122(,,,y k x M x y N x y =,将直线方程代入椭圆方程消去y ,利用根与系数的关系,再利用两点间的距离公式表示出||,||EM EN ,再计算||||EM EN 与2OP 比较可求出t 的值,②当OP 的斜率不存在时,可得||OP =MN的方程为x ||||EM EN 的值,进而可求出t (1)由题意可得24a =,所以2a =.因为点(1,32)在椭圆C 上,所以221914a b +=,解得23b =.所以椭圆C 的标准方程为22143x y +=.(2)①当OP 的斜率存在时,设直线OP 的方程为y kx =.联立方程,得22143y kxx y =⎧⎪⎨+=⎪⎩解得221234x k =+,2221234k y k =+.解得()2222221211212||343434k k OP k k k+=+=+++,设直线MN的方程为()()1122(,,,y k x M x y N x y =-.联立方程,得(22143y k x x y ⎧=-⎪⎨⎪+=⎩化简,得()22223412120k x x k +=+-=.因为点E0)在椭圆内部,所0∆>,221213221212,3434k x x x x k k-+=⋅=++,所以1||EM x =-.同理可得2||EN x =所以()(())22121212||||113EM EN kx xk x x x x ⋅=+=+⋅++()()22222223112122413343434k k kk k k k +-=+⋅-+=+++,假设存在实数(0)t t >),使得||,||,||EM t OP EN 构成等比数列,则22||||||EM EN t OP ⋅=.所以()()22222311213434k k tk k ++=⋅++.解得214t=.四为1t >,所以12t =,②当OP 的斜率不存在时,||OP =MN 的方程为x =x =22143x y +=,得234y =.所以||||2EM EN ==,当||,||,||EM t OP EN 构成等比数列时,22||||||EM EN t OP ⋅=,即2334t =.因为0t >,所以12t =.综上所述,存在实数12t =,使得||,||,||EM t OP EN 构成等比数列.22.在平面直角坐标系xOy 中,曲线C 的参数方程为x y αααα⎧=-⎪⎨=+⎪⎩(α为参数),以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.直线l 的极坐标方程为()cos sin 3m m ρθθ++=l 与曲线C 交于A ,B 两点.(1)求曲线C 的普通方程和直线l 的直角坐标方程;(2)过A ,B 分别作l 的垂线与x 轴交于C ,D 两点,若AB =CD .【答案】(1)2212x y +=,30mx y m ++=;(2)4.【解析】【分析】(1)消参法求曲线C 的普通方程,公式法求直线l 的直角坐标方程.(2)由(1)所得普通方程,结合圆中弦长、半径、弦心距的几何关系求圆心到直线l 的距离,再利用点线距离公式列方程求参数m ,即可得直线的倾斜角大小,由AB 、CD 的关系求CD 即可.(1)由题意,消去参数α,得曲线C 的普通方程为2212x y +=.将cos x ρθ=,sin y ρθ=代入()cos sin 3m m ρθθ++得直线l的直角坐标方程为30mx y m ++=.(2)设圆心到直线l:30mx y m ++=的距离为d,则AB =3d =.3=,解得3m =-.所以直线l的方程为60x +=,则直线l 的倾斜角为30θ=︒.所以4cos30AB CD ==︒.23.在平面直角坐标系xOy中,已知直线340x y ++=与圆1C :222x y r +=相切,另外,椭圆2C :()222210x y a b a b +=>>的离心率为32,过左焦点1F 作x 轴的垂线交椭圆于C ,D 两点.且1CD =.(1)求圆1C 的方程与椭圆2C 的方程;(2)经过圆1C 上一点P 作椭圆2C 的两条切线,切点分别记为A ,B ,直线PA ,PB 分别与圆1C 相交于M ,N 两点(异于点P ),求△OAB 的面积的取值范围.【答案】(1)225x y +=,2214x y +=;(2)4,15⎡⎤⎢⎥⎣⎦.【解析】【分析】(1)由直线与圆的相切关系及点线距离公式求参数r ,即可得圆1C 的方程,根据椭圆离心率、22b CD a=及椭圆参数关系求出a 、b 、c ,即可得椭圆2C 的方程.(2)设()11,A x y 、()22,B x y 、()00,P x y ,讨论直线PA ,PB 斜率存在性,则直线PA 为()111y k x x y =-+、直线PB 为()222y k x x y =-+,联立椭圆方程并结合所得一元二次方程0∆=求1k 、2k ,进而得直线PA 为1114x x y y +=、直线PB 为2214x xy y +=,结合P 在直线PA ,PB 上有AB 为0014x xy y +=,联立椭圆方程,应用韦达定理、弦长公式、点线距离公式,结合三角形面积公式得0OAB S = .(1)由题设,圆1C :222x y r +=的圆心为()0,0,因为直线340x y ++=与圆1C相切,则r ==所以圆1C 的方程为225x y +=,因为椭圆2Cc e a ==c =,由221b CD a==,则22a b =,又222a b c =+,所以22324a a a =+,解得2a =,1b =,所以椭圆2C 的方程为2214x y +=.综上,圆1C 为225x y +=,椭圆2C 为2214x y +=.(2)设点()11,A x y ,()22,B x y ,()00,P x y .当直线PA ,PB 斜率存在时,设直线PA ,PB 的斜率分别为1k ,2k ,则直线PA 为()111y k x x y =-+,直线PB 为()222y k x x y =-+.由()11122440y k x x y x y ⎧=-+⎨+-=⎩,消去y 得:()()()22211111111148440k x k y k x x y k x ++-+--=.所以()()()2222111111116441444k y k x k y k x ⎡⎤∆=--+--⎣⎦.令0∆=,整理得()2221111114210x k x y k y -++-=,则11111122111444x y x y x k x y y --=-==-,所以直线PA 为()11114x y x x y y -=-+,化简得:22111144x x y y y x +=+,即1114x x y y +=.经验证,当直线PA 斜率不存在时,直线PA 为2x =或2x =-也满足1114x xy y +=.同理,可得直线PB 为2214x xy y +=.因为()00,P x y 在直线PA ,PB 上,所以101014x x y y +=,202014x xy y +=.综上,直线AB 为0014x xy y +=.由00221444x xy y x y ⎧+=⎪⎨⎪+=⎩,消去y 得:()22200035816160y x x x y +-+-=.所以01220835x x x y +=+,21220161635y x x y -=+.所以12AB x =-=)20203135y y +==+.又O 到直线AB的距离d ==所以)20200311235OABy S y +=⋅+ t =,[]1,4t ∈,则24444OAB t S t t t∆==++,又[]44,5t t+∈,所以△OAB 的面积的取值范围为4,15⎡⎤⎢⎥⎣⎦.【点睛】关键点点睛:第二问,设点及直线PA ,PB 的方程,联立椭圆结合相切关系求参数关系,进而确定PA ,PB 的方程,由P 在直线PA ,PB 上求直线AB 的方程,再联立椭圆并应用韦达定理、弦长公式、点线距离公式求三角形面积的范围.24.已知点A ,B 是抛物线x 2=2py (p 为常数且p >0)上不同于坐标原点O 的两个点,且0OA OB ⋅= .(1)求证:直线AB 过定点;(2)过点A 、B 分别作抛物线的切线,两切线相交于点M ,记 OMA 、 OAB 、 OMB 的面积分别为S 1、S 2、S 3;是否存在定值λ使得22s =λS 1S 3?若存在,求出λ值;若不存在,请说明理由.【答案】(1)证明见解析(2)存在,4λ=【解析】【分析】(1)设11(,)A x y ,22(,)B x y ,设直线AB 方程为y kx t =+,代入抛物线方程中,消去y ,。
平面解析几何经典题(含答案)

平面解析几何一、直线的倾斜角与斜率1、直线的倾斜角与斜率、直线的倾斜角与斜率(1)倾斜角a 的范围000180a £<(2)经过两点的直线的斜率公式是(3)每条直线都有倾斜角,但并不是每条直线都有斜率2.两条直线平行与垂直的判定(1)两条直线平行对于两条不重合的直线12,l l ,其斜率分别为12,k k ,则有1212//l l k k Û=。
特别地,当直线12,l l 的斜率都不存在时,12l l 与的关系为平行。
的关系为平行。
(2)两条直线垂直如果两条直线12,l l 斜率存在,设为12,k k ,则12121l l k k ^Û=-注:两条直线12,l l 垂直的充要条件是斜率之积为-1,这句话不正确;由两直线的斜率之积为-1,可以得出两直线垂直,反过来,两直线垂直,斜率之积不一定为-1。
如果12,l l 中有一条直线的斜率不存在,另一条直线的斜率为0时,12l l 与互相垂直。
互相垂直。
二、直线的方程1、直线方程的几种形式名称名称方程的形式方程的形式 已知条件已知条件 局限性局限性 点斜式点斜式为直线上一定点,k 为斜率为斜率 不包括垂直于x 轴的直线轴的直线 斜截式斜截式k 为斜率,b 是直线在y 轴上的截距轴上的截距 不包括垂直于x 轴的直线轴的直线 两点式两点式是直线上两定点是直线上两定点 不包括垂直于x 轴和y 轴的直线直线截距式截距式a 是直线在x 轴上的非零截距,b 是直不包括垂直于x 轴和y 轴或线在y 轴上的非零截距轴上的非零截距过原点的直线过原点的直线 一般式一般式A ,B ,C 为系数为系数 无限制,可表示任何位置的直线直线 三、直线的交点坐标与距离公式三、直线的交点坐标与距离公式1.两条直线的交点设两条直线的方程是,两条直线的交点坐标就是方程组的解,若方程组有唯一解,则这两条直线相交,此解就是交点的坐标;若方程组无解,则两条直线无公共点,此时两条直线平行;反之,亦成立。
平面几何100题 70页

61.设ω是△ABC的外接圆,ΓA是与线段AB、AC相切且与ω内切的圆,ΓB是与线段BA、BC相切且与ω内切的圆,ΓC是与线段CA、CB相切且与ω内切的圆.设过B、C且与ΓA 相切的圆(不同于ω)切ΓA于X,过C、A且与ΓB相切的圆(不同于ω)切ΓB于Y,过A、B且与ΓC相切的圆(不同于ω)切ΓC于Z.证明:AX、BY、CZ三线共点.62.设⊙I是△ABC的内切圆,⊙u、⊙v、⊙w分别是过点B和点C且与⊙I相切的圆、过点A和点C且与⊙I相切的圆、过点B和点A且与⊙I相切的圆.设P、Q、R、S、T、U分别是⊙w与BC、⊙v与BC、⊙v与AB、⊙u与AB、⊙u与CA、⊙w与AC的交点(均不同于A、B、C).I1、I2分别是△ARQ、△BST的内心,类似定义I3、I4、I5、I6.I A是△AST∠SAT内的旁心,类似定义I B、I C.求证∶△I A I2I3、△I B I6I1、△I C I4I5的欧拉线共点.63.以凸四边形ABCD为边长向外作正方形AE1E2B、BF1F2C、CG1G2D、DH1H2A.连接AF1、BG1、CH1、DE1交出四边形A'B'C'D',连接DF2、AG2、BH2、CE2交出四边形A''B''C''D''.证明∶A'A''、B'B''、C'C''、D'D''交出的四边形是正方形.64.圆内接四边形ABCD中,直线AC、BD交于E,直线AB、CD交于F,直线BC、DA交于G.设△ABE的外接圆与直线CB交于B、P两点,△ADE的外接圆与直线CD交于D、Q两点.设直线FP、GQ交于点M,证明∶AM⊥AC.65.设⊙X、⊙Y、⊙Z分别为△ABC∠BAC、∠ABC、∠BCA内的旁切圆,D、E、F、G、H、I分别是⊙Z与AC、⊙Z与BC、⊙X与AB、⊙X与AC、⊙Y与BC、⊙Y与AB的切点.FD、GI交于J,IE、HF交于K,EG、DH交于L,设M、N、O、P、Q、R分别是KL、LJ、JK、BC、CA、AB的中点.证明∶直线MP、NQ、OR三线共点.66.已知凸六边形ABCDEF既有外接圆又有内切圆,记△ABC、△BCD、△CDE、△DEF、△EFA、△FAB的内切圆分别为ωb、ωc、ωd、ωe、ωf、ωa.l AB表示ωb、ωa的另一条外公切线(不为AB),类似定义l BC、l CD、l DE、l EF、l FA.设l FA与l AB的交点为A1,类似定义B1、C1、D1、E1、F1.若六边形A1B1C1D1E1F1为凸六边形,证明:该六边形的对角线共点.67.已知圆弧Γ1、Γ2、Γ3均过点A、C,且在直线AC同侧,Γ2在Γ1与Γ3之间,B是线段AC上一点,由B引三条射线h1、h2、h3,与Γ1、Γ2、Γ3在直线AC的同侧,且h2在h1与 h3之间.设h i与Γj(i,j=1,2,3)的交点为V ij.由线段V ij V il、V kj V kl及弧V ij V kj、弧V il V kl构成的曲边四边形记为V ij V kj V kl V il,若存在一个圆与其两条线段和两条弧均相切,则称这个圆为这个曲边四边形的内切圆.证明:若曲边四边形VV21V22V12、V12V22V23V13、V21V31V32V2211均有内切圆,则曲边四边形VV32V33V23也有内切圆.2268.设△ABC的内心为I,⊙I分别切边BC,CA,AB于点D、E、F,设AI与DE、DF交于点M、N,以MN为直径的圆交BC于P、Q.已知△APQ的外接圆与⊙I切于R,△ABC 的外接圆与九点圆切于Fe,设RFe与DE、DF分别交于点M'、N'.以M'N'为直径的圆交BC 于点P'、Q'.证明:△AP'Q'的外接圆与⊙I的根轴平分线段BC.69.设I是△ABC的内心,∠BAC、∠ABC、∠BCA的内角平分线分别交对边于点D、E、F.记H是△DEF垂心.证明:IH与△ABC的欧拉线平行.70.设⊙O、⊙P、⊙Q分别是△ABC∠BAC、∠CBA、∠ACB内的旁切圆,G、H、I、J、K、L分别是⊙P与AB、⊙Q与AC、⊙Q与BC、⊙O与AB、⊙O与AC、⊙P与BC的切点.证明∶△JKD、△LGE、△HIF、△ABC的欧拉线共点.71.△ABC中,O为外心,K为△ABC九点圆圆心关于△ABC的等角共轭点.K在BC、CA、AB上的射影分别为D、E、F,H是△DEF垂心.证明:O、K、H共线.72.已知H、I分别为△ABC垂心、内心,D、E、F分别在射线AH、BH、CH上,且AD=BE=CF=2r, 这里r是△ABC的内切圆半径.证明:I也为△DEF内心.73.已知B、I1、I2、C是⊙M上顺次四点,BI1与CI2交于A,△I1I2M的外接圆与AB、AC再次交于M1、M2,点O'满足M1O'∥CI1,M2O'∥BI2.X、Y为△ABC的一组等角共轭点,D、E分别在AB、AC上使得XD∥CI1、XE∥BI2,N为△BMC外接圆弧BC(不含M)的中点,XN与△BMC外接圆的另一个交点为F.证明:X、Y、O'共线当且仅当△DEF外接圆与△I1I2M的外接圆相切.74.设△ABC∠BAC内的旁切圆切AB、AC于G、F,∠ABC内的旁切圆⊙P切AB、AC于E、N,∠ACB内的旁切圆⊙Q切AB、AC于M、D.直线DE、MN分别交⊙Q于H、J,交⊙P 于I、K.HC、BI交于X,JF、KG交于Y,证明∶∠BAX=∠CAY.75.△ABC的内切圆⊙I切BC于D,连接AD交⊙I于J,K在JD上且DK=AJ,若BJ⊥CJ,证明:I、K关于△JBC等角共轭.76.O为△ABC外心,BC、CA上的旁切圆切点分别是X、Y,AX、BY交于点N.圆Γ1切BA、 CA延长线于E、D使得AD=AE=BC,类似地定义Γ2、Γ3.⊙U为与Γ1、Γ2、Γ3均外切的圆,证明:N、O、U共线.77.△ABC内切圆⊙I切BC于D,∠ACB内的旁切圆⊙P分别切BC、AB、CA于E、F、G,∠ABC内的旁切圆⊙Q分别切BC、CA、AB于H、J、K,CF与⊙P交于F、M两点,BJ与⊙Q交于J、N两点.证明:MJ、NF、AD共点.78.P为圆外切四边形ABCD内任意一点,AP、DP分别交BC于N、M.证明:△APD、△MPN、△ABN、△CDM四个三角形的内心共圆.79.设⊙I是△ABC的内切圆,△BCD外接圆⊙O1、△CAE外接圆⊙O2、△ABF外接圆⊙O3分别与⊙I内切于点D、E、F.GH与ST、JK与NP、LM与QR分别是⊙O2与⊙O3、⊙O1与⊙O2、⊙O3与⊙O1的外公切线(L、N、R、K在⊙O1上,P、H、J、S在⊙O2上,G、Q、T、M在⊙O3上,GH、TS与A分别在BC的同侧、异侧,LM、RQ与B分别在AC的同侧、异侧,JK、YM与C分别在AB的同侧、异侧).设△GHF、△JKE、△LMD外接圆分别为ω1、ω2、ω3,X、Y、Z分别是ω2与ω3、ω1与ω3、ω1与ω2的交点且X、A在BC异侧,Y、 C 在BA异侧,Z、B在AC异侧.证明∶S△KSX•S△MNY•S△HQZ=S△LTX•S△GPY•S.△RJZ80.圆外切四边形ABCD中两点P、Q满足∠DPA+∠BPC=∠DQA+∠BQC,I1、I2、I3、I4、I11、I22、I33、I44分别是△PAB、△PBC、△PCD、△PDA、△QAB、△QBC、△QCD、△QDA 的内心.证明:I1、I2、I3、I4共圆当且仅当I11、I22、I33、I44共圆.81.△ABC的内切圆分别切AC、AB于E、F.P、Q分别为边AC、AB上的旁切圆切点.点M 为BC中点,PQ、EF交于R.设△ABC九点圆与内切圆切于K,证明:M、R、K共线.82.凸四边形ABCD中,△ABC、△BCD、△CDA、△DAB的内心分别为I D、I A、I B、I C,∠BAC与∠BDC的角平分线交于点E,∠ABD与∠ACD的角平分线交于点F,线段I D I A、I B I C、EF的中点分别为X、Y、Z.证明:X、Y、Z三点共线.83.设ω1、ω2分别是过A、C且与△ABC内切圆内切于J的圆与过B、A且与△ABC内切圆内切于K的圆.设Q、R分别是ω1、ω2与BC的交点,ω1与AB交于P,ω2与AC交于S,X 是△CSR∠C内的旁心,Y是△BPQ∠B内的旁心,M是△BSR的内心,N是△CPQ的内心. 证明:四边形XYMN是矩形.84.设圆Γ过B,C且与△ABC的内切圆⊙I内切于点J,延长AJ交BC于K,交Γ于L.证明:(KB/KC)2=(LB/LC)3.85.⊙I、⊙J、⊙K与⊙O外切于X、Y、Z,EH、FL、MG分别是⊙I与⊙K、⊙I与⊙J、⊙J 与⊙K的外公切线且均与⊙O相交,并且E、F、G、H、L、M均为切点.HG与ML、EF与HG、EF与ML分别交于点U、V、W.证明:YW·XV·ZU=WX·VZ·UY.86.设I、O分别是△ABC的内心、外心,U、V分别为⊙O与⊙I的外位似中心与内位似中心,设E、F、Y、Z分别是BI与AC、CI与AB、BO与AC、CO与AB的交点.证明:U、E、F共线的充要条件是V、Y、Z共线.87.设P、Q是△ABC的一对等角共轭点且△ABC的重心G与P、Q共线.D、E、F分别是AP 与BC、BP与AC、CP与AB的交点,AQ、BQ、CQ分别与△ABC外接圆再次交于点X、Y、Z,证明:△ADX、△BEY、△CFZ外接圆有公共的根轴.88.给定△ABC,证明:在△ABC所在平面内存在唯一的一点P,使得△ABC、△PAB、△PBC、△PCA的欧拉线互相平行.89.设N为△ABC的九点圆圆心,N在BC、CA、AB上的射影分别为D、E、F,R为N 关于△DEF的等角共轭点,X是△AEF的九点圆圆心.证明:RX垂直于BC.90.设O、I a、I b、I c分别是△ABC的外心、∠BAC内的旁心、∠ABC内的旁心、∠BCA内的旁心.设与⊙Ib、⊙I c外切且与⊙O内切的圆与⊙O切于X,类似定义Y、Z.证明:AX、BY、CZ三线共点.91.O为△ABC外心,P、Q为△ABC的一对等角共轭点.设D、E、F分别为AP与BC、BP与CA、CP与AB的交点.设一条与OQ垂直的直线分别与BC、CA、AB交于点X、Y、Z.证明:△ADX外接圆、△BEY外接圆、△CFZ外接圆有一条公共的根轴.92.设I、O分别为△ABC的内心、外心,D、E、F分别为AI与BC、BI与AC、CI与 AB的交点.设ω为与AB、AC相切且与⊙O内切的圆,过E,F作ωaa的切线(不同于直线AB、AC)交于D1,X为ωa与⊙O切点,类似定义E1、F1、Y、Z.证明:XD1、YE1、ZF1、OI四线共点.93.设P为△ABC内一点,D、E、F分别是AP与BC、BP与AC、CP与AB的交点.设△DEF外接圆与直线BC另一个交点为X,O为△ABC外心,T为△DEF垂心,X'为X 关于直线EF的对称点.证明:AX'、BC、OT三线共点.。
(精心整理)平面几何经典难题及解答

平面几何经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC0,∠EBA =200,求∠BED 的度数.APCBACBPDA CBPD经典难题解答:经典难题(一)1.如下图做GH⊥AB,连接EO。
平面几何100题2.0版61-100,1'-30'

61.设ω是△A B C的外接圆,ΓA是与线段A B、A C相切且与ω内切的圆,ΓB是与线段B A、B C相切且与ω内切的圆,ΓC是与线段C A、C B相切且与ω内切的圆.设过B、C且与ΓA 相切的圆(不同于ω)切ΓA于X,过C、A且与ΓB相切的圆(不同于ω)切ΓB于Y,过A、B且与ΓC相切的圆(不同于ω)切ΓC于Z.证明:A X、B Y、C Z三线共点.62.设⊙I是△A B C的内切圆,⊙u、⊙v、⊙w分别是过点B和点C且与⊙I相切的圆、过点A和点C且与⊙I相切的圆、过点B和点A且与⊙I相切的圆.设P、Q、R、S、T、U分别是⊙w与B C、⊙v与B C、⊙v与A B、⊙u与A B、⊙u与C A、⊙w与A C的交点(均不同于A、B、C).I1、I2分别是△A R Q、△B S T的内心,类似定义I3、I4、I5、I6.I A是△A S T∠S A T内的旁心,类似定义I B、I C.求证∶△I A I2I3、△I B I6I1、△I C I4I5的欧拉线共点.63.以凸四边形A B C D为边长向外作正方形A E1E2B、B F1F2C、C G1G2D、D H1H2A.连接A F1、B G1、C H1、D E1交出四边形A'B'C'D',连接D F2、A G2、B H2、C E2交出四边形A''B''C''D''.证明∶A'A''、B'B''、C'C''、D'D''交出的四边形是正方形.64.圆内接四边形A B C D中,直线A C、B D交于E,直线A B、C D交于F,直线B C、D A交于G.设△A B E的外接圆与直线C B交于B、P两点,△A D E的外接圆与直线C D交于D、Q两点.设直线F P、G Q交于点M,证明∶A M⊥A C.65.设⊙X、⊙Y、⊙Z分别为△A B C∠B A C、∠A B C、∠B C A内的旁切圆,D、E、F、G、H、I分别是⊙Z与A C、⊙Z与B C、⊙X与A B、⊙X与A C、⊙Y与B C、⊙Y与A B的切点.F D、G I交于J,I E、H F交于K,E G、D H交于L,设M、N、O、P、Q、R分别是K L、L J、J K、B C、C A、A B的中点.证明∶直线M P、N Q、O R三线共点.66.已知凸六边形A B C D E F既有外接圆又有内切圆,记△A B C、△B C D、△C D E、△D E F、△E F A、△F A B的内切圆分别为ωb、ωc、ωd、ωe、ωf、ωa.l A B表示ωb、ωa的另一条外公切线(不为A B),类似定义l B C、l C D、l D E、l E F、l F A.设l F A与l A B的交点为A1,类似定义B1、C1、D1、E1、F1.若六边形A1B1C1D1E1F1为凸六边形,证明:该六边形的对角线共点.67.已知圆弧Γ1、Γ2、Γ3均过点A、C,且在直线A C同侧,Γ2在Γ1与Γ3之间,B是线段A C上一点,由B引三条射线h1、h2、h3,与Γ1、Γ2、Γ3在直线A C的同侧,且h2在h1与h3之间.设h i与Γj(i,j=1,2,3)的交点为V i j.由线段V i j V i l、V k j V k l及弧V i j V k j、弧V i l V k l构成的曲边四边形记为V i j V k j V k l V i l,若存在一个圆与其两条线段和两条弧均相切,则称这个圆为这个曲边四边形的内切圆.证明:若曲边四边形V11V21V22V12、V12V22V23V13、V21V31V32V22均有内切圆,则曲边四边形V22V32V33V23也有内切圆.68.设△A B C的内心为I,⊙I分别切边B C,C A,A B于点D、E、F,设A I与D E、D F交于点M、N,以M N为直径的圆交B C于P、Q.已知△A P Q的外接圆与⊙I切于R,△A B C 的外接圆与九点圆切于F e,设R F e与D E、D F分别交于点M'、N'.以M'N'为直径的圆交B C 于点P'、Q'.证明:△A P'Q'的外接圆与⊙I的根轴平分线段B C.69.设I是△A B C的内心,∠B A C、∠A B C、∠B C A的内角平分线分别交对边于点D、E、F.记H是△D E F垂心.证明:I H与△A B C的欧拉线平行.70.设⊙O、⊙P、⊙Q分别是△A B C∠B A C、∠C B A、∠A C B内的旁切圆,G、H、I、J、K、L分别是⊙P与A B、⊙Q与A C、⊙Q与B C、⊙O与A B、⊙O与A C、⊙P与B C的切点.证明∶△J K D、△L G E、△H I F、△A B C的欧拉线共点.71.△A B C中,O为外心,K为△A B C九点圆圆心关于△A B C的等角共轭点.K在B C、C A、A B上的射影分别为D、E、F,H是△D E F垂心.证明:O、K、H共线.72.已知H、I分别为△A B C垂心、内心,D、E、F分别在射线A H、B H、C H上,且A D=B E=C F=2r,这里r是△A B C的内切圆半径.证明:I也为△D E F内心.73.已知B、I1、I2、C是⊙M上顺次四点,B I1与C I2交于A,△I1I2M的外接圆与A B、A C 再次交于M1、M2,点O'满足M1O'∥C I1,M2O'∥B I2.X、Y为△A B C的一组等角共轭点,D、E分别在A B、A C上使得X D∥C I1、X E∥B I2,N为△B M C外接圆弧B C(不含M)的中点,X N与△B M C外接圆的另一个交点为F.证明:X、Y、O'共线当且仅当△D E F外接圆与△I1I2M的外接圆相切.74.设△A B C∠B A C内的旁切圆切A B、A C于G、F,∠A B C内的旁切圆⊙P切A B、A C于E、N,∠A C B内的旁切圆⊙Q切A B、A C于M、D.直线D E、M N分别交⊙Q于H、J,交⊙P 于I、K.H C、B I交于X,J F、K G交于Y,证明∶∠B A X=∠C A Y.75.△A B C的内切圆⊙I切B C于D,连接A D交⊙I于J,K在J D上且D K=A J,若B J⊥C J,证明:I、K关于△J B C等角共轭.76.O为△A B C外心,B C、C A上的旁切圆切点分别是X、Y,A X、B Y交于点N.圆Γ1切B A、C A延长线于E、D使得A D=A E=B C,类似地定义Γ2、Γ3.⊙U为与Γ1、Γ2、Γ3均外切的圆,证明:N、O、U共线.77.△A B C内切圆⊙I切B C于D,∠A C B内的旁切圆⊙P分别切B C、A B、C A于E、F、G,∠A B C内的旁切圆⊙Q分别切B C、C A、A B于H、J、K,C F与⊙P交于F、M两点,B J与⊙Q交于J、N两点.证明:M J、N F、A D共点.78.P为圆外切四边形A B C D内任意一点,A P、D P分别交B C于N、M.证明:△A P D、△M P N、△A B N、△C D M四个三角形的内心共圆.79.设⊙I是△A B C的内切圆,△B C D外接圆⊙O1、△C A E外接圆⊙O2、△A B F外接圆⊙O3分别与⊙I内切于点D、E、F.G H与S T、J K与N P、L M与Q R分别是⊙O2与⊙O3、⊙O1与⊙O2、⊙O3与⊙O1的外公切线(L、N、R、K在⊙O1上,P、H、J、S在⊙O2上,G、Q、T、M在⊙O3上,G H、T S与A分别在B C的同侧、异侧,L M、R Q与B分别在A C的同侧、异侧,J K、Y M与C分别在A B的同侧、异侧).设△G H F、△J K E、△L M D外接圆分别为ω1、ω2、ω3,X、Y、Z分别是ω2与ω3、ω1与ω3、ω1与ω2的交点且X、A在B C异侧,Y、C在B A异侧,Z、B在A C异侧.证明∶S△K S X•S△M N Y•S△H Q Z=S△L T X•S△G P Y•S△R J Z.80.圆外切四边形A B C D中两点P、Q满足∠D P A+∠B P C=∠D Q A+∠B Q C,I1、I2、I3、I4、I11、I22、I33、I44分别是△P A B、△P B C、△P C D、△P D A、△Q A B、△Q B C、△Q C D、△Q D A 的内心.证明:I1、I2、I3、I4共圆当且仅当I11、I22、I33、I44共圆.81.△A B C的内切圆分别切A C、A B于E、F.P、Q分别为边A C、A B上的旁切圆切点.点M 为B C中点,P Q、E F交于R.设△A B C九点圆与内切圆切于K,证明:M、R、K共线.82.凸四边形A B C D中,△A B C、△B C D、△C D A、△D A B的内心分别为I D、I A、I B、I C,∠B A C与∠B D C的角平分线交于点E,∠A B D与∠AC D的角平分线交于点F,线段ID I A、I B I C、E F的中点分别为X、Y、Z.证明:X、Y、Z三点共线.83.设ω1、ω2分别是过A、C且与△A B C内切圆内切于J的圆与过B、A且与△A B C内切圆内切于K的圆.设Q、R分别是ω1、ω2与B C的交点,ω1与A B交于P,ω2与A C交于S,X 是△C S R∠C内的旁心,Y是△B P Q∠B内的旁心,M是△B S R的内心,N是△C P Q的内心.证明:四边形X Y M N是矩形.84.设圆Γ过B,C且与△A B C的内切圆⊙I内切于点J,延长A J交B C于K,交Γ于L.证明:(K B/K C)2=(L B/L C)3.85.⊙I、⊙J、⊙K与⊙O外切于X、Y、Z,E H、F L、M G分别是⊙I与⊙K、⊙I与⊙J、⊙J 与⊙K的外公切线且均与⊙O相交,并且E、F、G、H、L、M均为切点.H G与M L、E F与H G、E F与M L分别交于点U、V、W.证明:Y W·X V·Z U=WX·V Z·U Y.86.设I、O分别是△A B C的内心、外心,U、V分别为⊙O与⊙I的外位似中心与内位似中心,设E、F、Y、Z分别是B I与A C、C I与A B、B O与A C、C O与A B的交点.证明:U、E、F 共线的充要条件是V、Y、Z共线.87.设P、Q是△A B C的一对等角共轭点且△A B C的重心G与P、Q共线.D、E、F分别是A P 与B C、B P与A C、C P与A B的交点,A Q、B Q、C Q分别与△A B C外接圆再次交于点X、Y、Z,证明:△A D X、△B E Y、△C F Z外接圆有公共的根轴.88.给定△A B C,证明:在△A B C所在平面内存在唯一的一点P,使得△A B C、△P A B、△P B C、△P C A的欧拉线互相平行.89.设N为△A B C的九点圆圆心,N在B C、C A、A B上的射影分别为D、E、F,R为N 关于△D E F的等角共轭点,X是△A E F的九点圆圆心.证明:R X垂直于B C.90.设O、I a、I b、I c分别是△A B C的外心、∠B A C内的旁心、∠A B C内的旁心、∠B C A 内的旁心.设与⊙I b、⊙I c外切且与⊙O内切的圆与⊙O切于X,类似定义Y、Z.证明:A X、B Y、C Z三线共点.91.O为△A B C外心,P、Q为△A B C的一对等角共轭点.设D、E、F分别为A P与B C、B P与C A、C P与A B的交点.设一条与O Q垂直的直线分别与B C、C A、A B交于点X、Y、Z.证明:△AD X外接圆、△BE Y外接圆、△CF Z外接圆有一条公共的根轴.92.设I、O分别为△A B C的内心、外心,D、E、F分别为A I与B C、B I与A C、C I与A B的交点.设ωa为与A B、A C相切且与⊙O内切的圆,过E,F作ωa的切线(不同于直线A B、A C)交于D1,X为ωa与⊙O切点,类似定义E1、F1、Y、Z.证明:X D1、Y E1、Z F1、O I 四线共点.93.设P为△A B C内一点,D、E、F分别是A P与B C、B P与A C、C P与A B的交点.设△D E F外接圆与直线B C另一个交点为X,O为△A B C外心,T为△D E F垂心,X'为X 关于直线E F的对称点.证明:A X'、B C、O T三线共点.94.给定△A B C及与一点P,设A P与B C、B P与C A、C P与A B的交点分别为D、E、F.证明:存在两点U、V使得V是U关于△A B C的等角共轭点,也是U关于△D E F的等角共轭点.95.△A B C的垂心为H,A H与B C交点为D.U、V为线段B C上两点使得∠B H U=∠C H V,P Q、R S为△A B C外接圆的两条弦且分别过U、V.证明:△A D P、△A D Q、△A D R、△A D S四个三角形的垂心共圆.96.△A B C的内心、外心、垂心分别是I、O、H.P为直线O I上一点,P a、P b、P c分别是P在B C、C A、A B上的射影.设A I、B I、C I与⊙O再次交于D、E、F,设D'、E'、F'分别为D关于P a、E关于P b、F关于P c的对称点.证明:D'、E'、F'、H四点共圆.97.△A B C外心为O,P为△A B C所在平面内一点,D、E、F分别为P在B C、A C、A B 上的射影,A P、B P、C P与⊙O再次交于点X、Y、Z.X'、Y'、Z'分别是X关于O D、Y关于O E、Z关于O F的对称点.证明:A X'、B Y'、C Z'三线共点.98.△A B C外心为O,共轭重心为K,D与A在直线B C同侧且△B C D为正三角形,J是A D 中垂线与B C交点,A J与⊙O再次交于T.证明:T关于△A B C的西姆松线平行于O K.99.P为△A B C内一点,D、E、F分别是A P与B C、B P与A C、C P与A B交点,X、Y、Z分别是P在B C、C A、A B上的射影.P关于△A B C的等角共轭点Q,O为△A B C外心,r为⊙O 半径.R在射线O Q上且O P·O Q=r2.△D E F外接圆与△X Y Z外接圆有两个不同的交点T1、T2.l1、l2分别为T1、T2关于△D E F的西姆松线,直线l3、l4使得l3∥l1且T1到l3的距离为T1到l1距离的两倍,l4∥l2且T2到l4的距离等于T2到l2距离的两倍(T1在l1、l3的同侧,T2在l2、l4的同侧).证明:l3、l4一条过P,一条过R.100.已知⊙O上顺次五点A、B、C、D、E,设ω1为与B C、A C相切且与⊙O内切的圆,ω2为与A D、B E相切且与⊙O内切的圆,ω3为与A D、B E相切且与⊙O外切的圆.证明:C向ω3所作的一条切线与ω1与ω2的一条公切线平行.1'.已知⊙O1与△A B C的A B、B C边相切且与△A B C的外接圆内切于E,⊙O2与△A B C的A C、B C边相切且与△A B C的外接圆内切于F,连接E O2、F O1交于X.证明:A X平分∠B A C.2'.一直线交△X1X2X3三边所在直线X2X3、X3X1、X1X2于A1、A2、A3.分别过A1、A2、A3作X2X3、X3X1、X1X2的垂线,三垂线交成△Y1Y2Y3.证明:直线A1A2A3平分△X1X2X3垂心和△Y1Y2Y3垂心的连线段.3'.设H为锐角△A B C的垂心,M为B C中点,⊙I1、⊙I2分别为△A B H、△A C H的内切圆.证明:⊙I1、⊙I2除A H外的另一条内公切线过M.4'.设△A B C的内切圆分别切B C、C A、A B于D、E、F.记D关于E F、E关于F D、F关于D E 的对称点分别为D’、E’、F’,V为△A B C的九点圆心.证明:V在△D’E’F’的欧拉线上.5'.△A B C内接与⊙O,H是△A B C的垂心,E、F分别是H关于直线A C、A B的对称点.O E与A C交于M,O F与A B交于N,作平行四边形A B D C,设X、Y、Z分别是H在M N、N D、M D边上的射影.证明:△X Y Z的外接圆与△A B C的九点圆相切.6'.已知⊙I为△A B C的内切圆,⊙U过B、C两点,⊙V与边A B、A C相切且与⊙U内切,l 为平行于B C且与⊙I相切的直线(l不与B C重合),L为⊙U上任意一点,过L作⊙I的切线交l于E、F.证明:△E F L的外接圆与⊙V相切.7'.设K是△A B C的共轭重心,P是△A B C内任意一点,P在B C、C A、A B的射影分别为X、Y、Z,G为△X Y Z的重心,D在A B C的外接圆上且满足D关于△A B C的西姆松线与直线K P平行.设直线A D、B C交于E;直线B D、A C交于F;直线E F、A B交于J.证明:J、K、G共线.8'.设H、I分别为△A B C的垂心、内心,A B、A C上的旁切圆切点分别为F、E,线段B E与C F相交于N.设H N中点为M,J在射线M I上满足J M·I M=M H²,直线I N与B C交于D,G在线段B C上且满足B G=C D.证明:G I=G J.9'.已知四边形A B C D为圆外切四边形,A C、B D的中垂线相交于P,设I1、I2、I3、I4分别为△A B P、△B C P、△C D P、△D A P的内心.证明:I1、I2、I3、I4四点共圆.10'.设四边形A B C D内接于⊙U,⊙V与线段A C、B D相切(与线段B C相交)且与⊙U内切于T,F为劣弧B C上任意一点,⊙P与线段A F、B C相切(与线段A B相交)且与⊙U内切.设M是⊙P与B C的切点,延长D M交⊙U于E.⊙Q与线段D E、B C相切(与线段C D相交)且与⊙U内切,⊙R与直线B F、C E相切且与⊙U外切于X.设N是⊙Q与B C的切点.证明:M、N、T、X四点共圆.。
平面几何100题(1)

平面几何100题1.非等腰锐角三角形ABC 的外接圆为ω,H 为△ABC 的垂心,M 是AB 的中点。
在不含C 的圆弧AB 上取点P、Q,使得∠ACP=∠BCQ<∠ACQ,过H 分别作CQ、CP 的垂线,垂足为R、S。
证明:P,Q,R,S 共圆且点M 是该圆的圆心。
2.在△ABC 中,点M、N、K 分别在边BC、CA、AB 上且不与顶点重合,若∠BAC=∠KMN 且∠ABC=∠KNM,则称△MNK 为完美三角形。
证明:如果在△ABC 中有两个具有共同顶点且不重合的完美三角形,则△ABC 是直角三角形。
3.四边形ABCD 满足AD//BC,∠ABC>90⁰,M 是线段AB 上不同于A、B 的一点,设△MAD、△MBC 的外心分别为21,O O 。
△D MO 1的外接圆不同于M 的交点为N。
求证:点N 在直线21O O 上。
4.在凸四边形(非平行四边形)ABCD 的对角线上分别取点B′、C′,使得△ACB′、△BDC′都为正三角形,其中点B 和B′位于AC 的同侧,点C 和C′位于BD 的同侧,如果CD AB C B +='',求∠BAD+∠CDA 的值。
5.给定一个凸六边形ABCDEF,其中AB//DE,BC//EF,CD//FA。
设BD 和AE、AC 和DF、CE 和BF 的交点分别为M、N、K。
证明:过M、N、K 分别作AB、CD、EF 的垂线交于同一点。
6.圆内接四边形ABCD 的对角线交于点K,点M 和N 分别是对角线AC 和BD 的中点,△ADM 和△BCM 的外接圆交于点M、L,证明:K,L,M,N(这些点两两不重合)四点共圆。
7.圆内接四边形ABCD 的外接圆为圆Ω且AB=AD,在线段BC、CD 上分别取点M、N,使得MN=BM+DN。
直线AM 交圆Ω于点P (不同于A),直线AN 交圆Ω于点Q (不同于A)。
求证:△APQ 的垂心在MN 上。
8.给定四边形ABCD,其中∠B=∠D=90⁰,在线段AB 上取点M 使得AD=AM。
