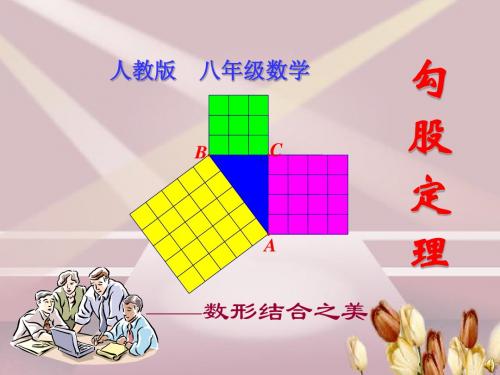
2019年春八年级数学下册第十七章勾股定理17.1勾股定理ppt课件新版新人教版
合集下载
八年级下册17勾股定理PPT课件(人教版)

1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:
17.1.1 勾股定理
1.你能发现图中的等腰直角三角形有什么性 质吗? 2.你能用三角形的边长表示正方形的面积吗?
3.你能发现直角 三角形三边长度 之间存在什么关 系吗?
好奇是人的本性! 观察图1-1,回答问题:
图1-1
图1-2
1.正方形A中 含有 9 个小 方格,即A的面 积是 9 单位 面积.
图1-3
图1-4
探索勾股定理
1.正方形A中 含有 16 个小 方格,即A的面 积是 16 单位 面积.
2.B的面积是 9 单位面
积. C的面积是 25 单位面
积.
好奇是人的本性!
观察图1-4,填表:
C的面积是
单位面积.
B的面积是
单位面积.
½ a2 + ab + ½ b2
=
½ c2 + ab
大正方形的面积可以表示为
c2 = a2 + b2
方法三
a
bc
½(a + b)(b + a) = ½c2 + 2(½ab) ½a2 + ab + ½b2 = ½c2 + ab
a2 + b2 = c2
c
a
b
练习:口答
1、在△ABC中,∠C=90°, ∠A 、 ∠B 、 ∠C 的对边分别
为a 、 b 、 c,
⑴若a=3,b=4,则c=__5 ; ⑵若a=5,c=13,则b=__12; ⑶若b=8,c=17,则a=__15 ;
,
直角三角形中,两直角边的平方和等于斜边的平方;
我们将利用拼图法来证明勾股定理:
17.1.1 勾股定理
1.你能发现图中的等腰直角三角形有什么性 质吗? 2.你能用三角形的边长表示正方形的面积吗?
3.你能发现直角 三角形三边长度 之间存在什么关 系吗?
好奇是人的本性! 观察图1-1,回答问题:
图1-1
图1-2
1.正方形A中 含有 9 个小 方格,即A的面 积是 9 单位 面积.
图1-3
图1-4
探索勾股定理
1.正方形A中 含有 16 个小 方格,即A的面 积是 16 单位 面积.
2.B的面积是 9 单位面
积. C的面积是 25 单位面
积.
好奇是人的本性!
观察图1-4,填表:
C的面积是
单位面积.
B的面积是
单位面积.
½ a2 + ab + ½ b2
=
½ c2 + ab
大正方形的面积可以表示为
c2 = a2 + b2
方法三
a
bc
½(a + b)(b + a) = ½c2 + 2(½ab) ½a2 + ab + ½b2 = ½c2 + ab
a2 + b2 = c2
c
a
b
练习:口答
1、在△ABC中,∠C=90°, ∠A 、 ∠B 、 ∠C 的对边分别
为a 、 b 、 c,
⑴若a=3,b=4,则c=__5 ; ⑵若a=5,c=13,则b=__12; ⑶若b=8,c=17,则a=__15 ;
,
直角三角形中,两直角边的平方和等于斜边的平方;
我们将利用拼图法来证明勾股定理:
八年级数学下册 第17章 勾股定理 17.1 勾股定理课件2 (新版)新人教版.pptx

17
【纠错园】 如图是一个长4 m,宽3 m,高2 m的有盖仓库,在其内壁 的A处(长的四等分点)有一只壁虎,B处(宽的三等分点) 有一只蚊子,求壁虎爬到蚊子处最短距离是多少.
18
19
【错因】本题考虑问题不全面,只考虑按长方体的高棱 展开,没考虑按长方体的长棱展开,漏掉其中一种情况.
20
13
【解析】把圆柱的侧面展开,得到如图所示的图形,
由题意知 1
AC=3,CE=205× =4, ∴AE= 32 4=2 5. ∴葛藤的最短长度为25尺.
答案:25
14
【备选例题】如图,长方体的底面边长分别为1cm和3cm, 高为6cm.如果用一根细线从点A开始经过4个侧面缠绕 一圈到达点B,那么所用细线最短需要( )
17.1 勾股定理 第2课时
1
【基础梳理】 1.勾股定理的应用 直角三角形中,根据勾股定理,已知两边可求第三边: Rt△ABC中,∠C=90°,a,b,c分别为内角A,B,C的对 边,(1)若已知边a,b,则c= a2 b2 ;(2)若已知边a,c,则 b= c2 a2 ;(3)若已知边b,c,则a= c2 b2.
10
11
知识点二 利用勾股定理解决立体图形中的最短路线 问题 【示范题2】(2017·东营中考)我国古代有这样一道数 学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤 自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意
12
是:如图所示,把枯木看作一个圆柱体,因一丈是十尺, 则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处 缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛 藤的最短长度是________尺.
2
2.立体图形中距离最短问题 (1)如图,圆柱的侧面展开图是_长__方__形__,点B的位置应 在长方形的边CD的_中__点__处,点A到点B的最短距离为线 段_A_B_的长度.
【纠错园】 如图是一个长4 m,宽3 m,高2 m的有盖仓库,在其内壁 的A处(长的四等分点)有一只壁虎,B处(宽的三等分点) 有一只蚊子,求壁虎爬到蚊子处最短距离是多少.
18
19
【错因】本题考虑问题不全面,只考虑按长方体的高棱 展开,没考虑按长方体的长棱展开,漏掉其中一种情况.
20
13
【解析】把圆柱的侧面展开,得到如图所示的图形,
由题意知 1
AC=3,CE=205× =4, ∴AE= 32 4=2 5. ∴葛藤的最短长度为25尺.
答案:25
14
【备选例题】如图,长方体的底面边长分别为1cm和3cm, 高为6cm.如果用一根细线从点A开始经过4个侧面缠绕 一圈到达点B,那么所用细线最短需要( )
17.1 勾股定理 第2课时
1
【基础梳理】 1.勾股定理的应用 直角三角形中,根据勾股定理,已知两边可求第三边: Rt△ABC中,∠C=90°,a,b,c分别为内角A,B,C的对 边,(1)若已知边a,b,则c= a2 b2 ;(2)若已知边a,c,则 b= c2 a2 ;(3)若已知边b,c,则a= c2 b2.
10
11
知识点二 利用勾股定理解决立体图形中的最短路线 问题 【示范题2】(2017·东营中考)我国古代有这样一道数 学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤 自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意
12
是:如图所示,把枯木看作一个圆柱体,因一丈是十尺, 则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处 缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛 藤的最短长度是________尺.
2
2.立体图形中距离最短问题 (1)如图,圆柱的侧面展开图是_长__方__形__,点B的位置应 在长方形的边CD的_中__点__处,点A到点B的最短距离为线 段_A_B_的长度.
八年级下册17.1 勾股定理 课件 (共30张PPT)
探究:生活中的数学问题 应用知识回归生活
1、一个门框尺寸如下图所示. ①若有一块长3米,宽0.8米的薄木板,能否通过此门? ②若薄木板长3米,宽1.5米呢? ③若薄木板长3米,宽2.2米呢?为什么?
对角线= 12 22 5
2.236 2.2
∴能通过此门.
想 一 想
2、小明的妈妈买了一部29英寸(74厘 米)的电视机。小明量了电视机的屏 幕后,发现屏幕只有58厘米长和46厘 米宽,他觉得一定是售货员搞错了。
2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
归纳定理: 勾股定理 (毕达哥拉斯定理)
如果直角三角形两直角边分
别为a,b,斜边为c,那么
勾a
c弦
a2 b2 c2
股b
即直角三角形两直角边的平方和等于
斜边的平方.
强调:勾股定理反映了直角三角形的 勾
股
三边关系。
一、总统证法 美国第20任总统-伽菲尔德
2、查阅有关勾股定理的历史资料,及 证明方法,与同学交流。
别为a,b,斜边为c,那么
勾a
c弦
a2 b2 c2
股b
即直角三角形两直角边的平方和等于
斜边的平方.
强调:勾股定理反映了直角三角形的 勾
股
三边关系。
变式运用:
cba
bca
cab
a
c
b
确定斜边
?
a2+b2 = c2 a2+c2 = b2 b2+c2 = a2
灵活运 用公式
c2=a2 +b2
a2= c2 - b2 b2= c2 - a2
人教版八年级数学下册《17.1勾股定理》课件 (共13张PPT)

这个世界上,从来没有谁比谁更优秀,只有谁比谁更努力。
很多人都去了,回来的时候每人拎着一只鸡,大家都很高兴!
人生,是一本太仓促的书,越认真越深刻;
越是优秀的人,越是努力,因为优秀从来不是与生俱来,从来不是一蹴而就。
人到中年,突然间醒悟许多,总算明白:人生,只有将世间的路一一走遍,才能到尽头;
一个土豪,每次出门都担心家中被盗,想买只狼狗栓门前护院,但又不想雇人喂狗浪费银两。
3.(1)已知直角三角形的两直角边的长分别为3和4,则第三边
的长为___5____;
(2)已知直角三角形的两边的长分别为3和4,则第三边的长为
__________.
4.求图17-1-1中直角三角形中未知的长度:b=____1_2___, c=____3_0____.
知识清单
知识点1 勾股定理 勾股定理内容:直角三角形两直角边的平方和等于斜__边__的_平__方_. 勾股定理表示方法:如果直角三角形的两直角边分别为a,b ,斜边为c,那么a_2_+__b_2_=__c_2____. 勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达 哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾, 较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数 学家商高就提出了“勾三,股四,弦五”形式的勾股定理, 后来人们进一步发现并证明了直角三角形的三边关系为:两 直角边的平方和等于斜边的平方.
生活,只有将尘世况味种种尝遍,才能熬出头。
勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.
人到中年,突然间醒悟许多,总算明白:人生,只有将世间的路一一走遍,才能到尽头;
如图17-1-7,一棵大树被台风刮断,若树在离地面9 m处折断,树顶端落在离树底部12 m处,则大树折断之前的高度为
人教版数学八年级下册:17.1 勾股定理 课件(共35张PPT)

探究 如图,以Rt△ 的三边为边向外作正方形,
其面积分别为 S1 、S2、S3,请同学们想一想
S1 、S2、S3 之间有何关系呢?
S2 + S3 =a2+b2
S1=c2
B
S1c a S2
b
A S3 C
∵a2+b2=c2
S2 + S3 = S1
探究S1、S2、S3之间的关系
S2
S3
1 2
a 2
2
1 2
b 2
2
1 a2 1 b2
8
8
S1
1 2
c 2
2
1
8
c2
由勾股定理得 a2+b2=c2
∴S2+S3=S1
S2
c
SS3 2
A
S1
S1
动手操作:例2如图,Rt△ABC中
,AC=8,BC=6,∠C=90°,分别 以AB、BC、AC为直径作三个半圆 ,那么阴影部分的面积为__24_ .
A
E
D
B
F
C
A
A =625
225
400
81
B =144
225
2、如图所示的图形中,所 有的四边形都是正方形,所 有的三角形都是直角三角形 ,其中最大的正方形的边长 是8厘米,则正方形A,B, C,D的面积之和是 __6_4_____平方厘米
利用勾股定理解决平面几何问题3——折叠中的计算问题
能算好算直接算,不能算不好算,设未知数,列方程(勾股定理、全等、相似等)
利用勾股定理解决平面几何问题1— —最短路径问题
八年级数学下册 第十七章 勾股定理 17.1 勾股定理(1)课件 (新版)新人教版.pptx

13
巩固提高
11. 如图,已知等边三角形ABC的边长是6cm。求: (1)高AD的长; (2)△ABC的面积 。
14
巩固提高
12. 已知直角三角形的两直边分别为3cm,4cm,则 正确的组合为(B)
①斜边边长为25cm ②斜边边长为5cm ③周长为 12cm ④面积为6cm2 ⑤面积为12cm2 A.①② B.②③④ C.②③⑤ D.①④
__c_2_=__a_2_+__b_2___.
3.如图所示的图形中,所有的四边形 都是正方形,三角形是直角三角形, 其中最大的正方形的边长为5,则正 方形A,B的面积的和为 25 .
3
8 分钟小测
4.如图,在Rt△ABC中,∠C=90°,
(1)如果a=3,b=4,则c=___5___; (2)如果a=6,b=8,则c=__1_0___; (3)如果a=5,b=12,则c=__1_3___; (4)如果a=15,b=20,则c=__2_5___.
15
巩固提高
13.如图,在10×6的正方形网格中,每个小正方 形的边长均为1,线段AB的端点A、B均在格点上. 分别在图和图中作出以AB为一腰的等腰△ABC ,使其顶角分别为直角和钝角,点C在格点上,并 计算两图中△ABC的周长。
16
巩固提高
17
A bc C aB
4
精典范例
知识点1.利用面积验证勾股定理 例1. 利用四个全等的直角三角形可以拼成如下图 所示的图形,这个图形被称为弦图.观察图形,验 证:c2=a2+b2.
5
变式练习
1 如图,三个正方形中的两个的面积S1=25,S2= 144,则另一个的面积S3为___1_6_9___.
精典范例
第十七章 勾股定理
巩固提高
11. 如图,已知等边三角形ABC的边长是6cm。求: (1)高AD的长; (2)△ABC的面积 。
14
巩固提高
12. 已知直角三角形的两直边分别为3cm,4cm,则 正确的组合为(B)
①斜边边长为25cm ②斜边边长为5cm ③周长为 12cm ④面积为6cm2 ⑤面积为12cm2 A.①② B.②③④ C.②③⑤ D.①④
__c_2_=__a_2_+__b_2___.
3.如图所示的图形中,所有的四边形 都是正方形,三角形是直角三角形, 其中最大的正方形的边长为5,则正 方形A,B的面积的和为 25 .
3
8 分钟小测
4.如图,在Rt△ABC中,∠C=90°,
(1)如果a=3,b=4,则c=___5___; (2)如果a=6,b=8,则c=__1_0___; (3)如果a=5,b=12,则c=__1_3___; (4)如果a=15,b=20,则c=__2_5___.
15
巩固提高
13.如图,在10×6的正方形网格中,每个小正方 形的边长均为1,线段AB的端点A、B均在格点上. 分别在图和图中作出以AB为一腰的等腰△ABC ,使其顶角分别为直角和钝角,点C在格点上,并 计算两图中△ABC的周长。
16
巩固提高
17
A bc C aB
4
精典范例
知识点1.利用面积验证勾股定理 例1. 利用四个全等的直角三角形可以拼成如下图 所示的图形,这个图形被称为弦图.观察图形,验 证:c2=a2+b2.
5
变式练习
1 如图,三个正方形中的两个的面积S1=25,S2= 144,则另一个的面积S3为___1_6_9___.
精典范例
第十七章 勾股定理
