最新版小学六年级数学题库 用正比例解决问题练习题
最新人教版六年级数学下册《配套练习与检测》比例解决问题专项训练

最新人教版六年级数学下册《比例》解决问题专项训练1. 根据下面的条件列出比例式,并解比例。
(1)两个内项分别是6和10,两个外项分别是x 和1.2。
(2)最大的一位数与最小的质数的比等于31与x 的比。
(3)34与x 的积等于31与87的积。
2.科技馆展示的“神舟六号”轨道舱模型高1.4米,直径1.2米,模型与实际数据的比是1:2,求“神舟六号”轨道舱的实际高度和直径各是多少?3.某地上午10时电线杆的高度与其影子的长度比是4:3,已知影子长是6㎝,求电线杆的高度。
4. 乐乐家距离学校3㎞,在比例尺为1:100000的地图上,乐乐家与学校的距离是多少?5.一段铁路长3000米,画在比例尺是多少的地图上铁路长为1.5㎝?6.光明小学教学楼的地基是长方形,它的长为72米,宽为14米。
用1:1000的比例尺把它画在图纸上,图上长方形的长和宽各是多少米?画出教学地基的平面图。
7.在能够一幅比例尺为1:500的平面图上量得一间长方形教室的长是3㎝,宽是2㎝。
求这间教室的图上面积和实际面积。
8.张强骑自行车从家到学校,如果每分钟行420米,要3分钟,实际上到校只用了4分钟,实际上每分钟行多少米?9.一种农药,药液与水的比是1:125,20千克药液需要加多少千克的水?10.一种农药,药液与水的比是1:125,现有400千克的水,配制这种农药需要多少千克的药液?11.一种农药,药液与水的比是1:125,如果有4千克的药液,能配制这种农药多少千克?12.圆圆看一本故事书,前5天看了80页,照这样计算,看完这本256页的故事书一共需要多少天?13.甲乙两地的距离在比例尺是1:20000000的地图上长4㎝,乙、丙两地相距500㎞,画在这幅地图上,应画多长?14.用边长是90㎝的方砖铺地需要2000块,如果改用40㎝的方砖铺地,需要多少块?15.一个机器零件的长度是0.5㎝,在比例尺40:1的图纸上,它的长度是多少米?16.在实验小学新校区的规划图上,长方形操场的长是28厘米,宽是22厘米,如果规划图的比例尺是1:400,这个操场实际占地是多少平方米? 如果在操场的四周建造护栏,护栏长多少米?17.用一批纸装订同样大小的练习本,如果每本30页,可装订120本。
六年级数学下册《用比例解决问题》练习题及答案解析

六年级数学下册《用比例解决问题》练习题及答案解析学校:___________姓名:___________班级:_____________一、选择题1.一条2厘米的线段,选用下面比例尺()画出的平面图最大。
A.1∶200B.1∶5000C.1∶1D.2∶12.老师买了同样数目的田格本、横线本和练习本。
他发给每个同学1个田格本、3个横线本和5个练习本。
这时横线本还剩24个,那么田格本和练习本共剩了()个。
A.48B.50C.54D.563.把一个圆柱削成一个最大的圆锥,削去的体积是48立方分米,圆柱的体积是()立方分米。
A.144B.24C.724.一幅地图的比例尺是1∶1000000,下列说法不正确的是()。
A.这是一个数值比例尺B.说明要把实际距离缩小为11000000后,再画在图纸上C.图上距离相当于实际距离的1 1000000D.图上1厘米相当于实际1000000米5.下列各数中,()不能与2、8、10组成比例。
A.58B.85C.52D.406.甲乙两个容积相同的瓶子分别装满盐水,已知甲瓶中盐、水的比是2∶3,乙瓶中盐、水的比是3∶5,现在把甲、乙两瓶水混合在一起,则混合盐水中,盐与盐水的比是()。
A.519B.521C.524D.31807.一个水池有甲乙两个水管。
单独开甲管,2小时可以把空池注满;单独开乙管,3小时可以把空池注满。
如果同时打开甲乙两管,()小时可以把空池注满。
A.1B.15C.115D.58.希望小学合唱队共有队员108人,则()一定不是男队员和女队员人数的比。
A.5∶4B.7∶5C.8∶7D.19∶17 9.表示x和y成正比例关系的式子是().A.x+y=9B.y=1.5x C.=0D.xy+1=510.学校把560棵树的种植任务,按照六年级三个班的人数分配给各班。
一班有47人,二班有45人,三班有48人。
二班应种树()。
A.192棵B.188棵C.180棵11.在一幅地图上,用20厘米的线段表示50千米的实际距离,那么这幅地图的比例尺是()。
正比例六年级练习题

正比例六年级练习题1. 小明骑自行车从家到学校的距离是5千米,花费的时间是20分钟。
如果小明骑自行车的速度保持不变,那么他骑自行车10千米要花费多长时间?解析:根据题意可知,小明骑自行车的速度是不变的,那么他骑自行车的速度可以用速度和时间的关系式 v = s / t 来表示。
假设他骑自行车10千米要花费的时间是 t1,那么根据题意可得: 5千米 / 20分钟 = 10千米 / t1。
求解上述比例式可以得到:t1 = (10千米 × 20分钟) / 5千米 = 40分钟。
答案:小明骑自行车10千米要花费40分钟。
2. 一箱苹果有24个,重4千克,那么重6千克的苹果需要多少个?解析:根据题意可知,苹果的重量和苹果的个数之间是成正比例的,苹果的重量可以用重量和个数的关系式 g = w / n 来表示。
假设重6千克的苹果需要的个数是 n1,那么根据题意可得: 4千克 / 24个 = 6千克 / n1。
求解上述比例式可以得到:n1 = (6千克 × 24个) / 4千克 = 36个。
答案:重6千克的苹果需要36个。
3. 甲用4根绳子拉一辆车,用了12分钟拉了100米;乙用6根绳子拉相同的车,需要多少时间才能拉行走200米?解析:根据题意可知,拉车的速度和所用的绳子的根数之间是成正比例的,速度可以用速度和时间的关系式 v = s / t 来表示。
假设乙用6根绳子拉相同的车需要的时间是 t2,那么根据题意可得: 4根绳子 / 12分钟 = 6根绳子 / t2。
求解上述比例式可以得到:t2 = (6根绳子 × 12分钟) / 4根绳子 = 18分钟。
答案:乙用6根绳子拉行走200米需要18分钟。
4. 甲种植一批小麦可以收获10千克,需要耕种10天;乙种植相同的一批小麦,需要多少天才能收获25千克?解析:根据题意可知,小麦的收获量和种植的天数之间是成正比例的,小麦的收获量可以用收获量和天数的关系式 y = x / t 来表示。
六年级数学下册典型例题系列之第六单元正比例和反比例在图表中的应用专项练习(解析版)(苏教版)

2021-2022学年六年级数学下册典型例题系列之第六单元正比例和反比例在图表中的应用专项练习(解析版)一、填空题。
1.(2021·河北邯郸·小升初真题)如图表示一辆汽车在公路上行驶的时间与路程的关系,这辆汽车行驶的时间与路程成()比例。
照这样计算,2.2小时行驶()千米。
【解析】(1)根据图可知:路程÷时间=速度(一定),商一定,所以路程和时间成正比例关系;(2)100÷1×2.2=100×2.2=220(千米)2.(2021·河北保定·小升初真题)观察关于购买衣服的统计表:购买衣服的数量和总价成( )比例。
【解析】70÷2=35105÷3=35140÷4=35175÷5=35210÷6=35总价÷数量=35(一定),商一定,所以购买衣服的数量和总价成正比例。
3.(2021·云南玉溪·六年级期末)如图表示一辆汽车在公路上行驶的时间与路程的关系,这辆汽车行驶的时间与路程成( )比例。
照这样计算,该汽车6.6时行驶( )km。
【解析】6.6×100=660(千米)这辆汽车行驶的时间与路程成正比例。
照这样计算,该汽车6.6时行驶660km。
4.(2021·陕西·延安市宝塔区蟠龙镇初级中学六年级期末)莎莎骑车到相距5千米的书店买书,买完书立刻返回家中。
如图是她离开家的距离与时间的统计图。
(1)莎莎去书店每小时行( )千米,用了( )分钟,这段时间内她骑车的路程和时间成( )比例。
(2)莎莎从书店返回家中的速度是每小时( )千米,用了( )分钟。
(3)莎莎返回时的速度比去时慢( )%。
【解析】(1)5÷0.5=10(千米),所以,莎莎去书店每小时行10千米,用了30分钟,这段时间内她骑车的路程和时间成正比例;(2)5÷1.25=4(千米),所以,莎莎从书店返回家中的速度是每小时4千米,用了75分钟;(3)(10-4)÷10=6÷10=60%所以,莎莎返回时的速度比去时慢60%。
完整版)六年级数学正比例练习题

完整版)六年级数学正比例练习题1.判断XXX的单价和购买XXX的数量与总价是否成正比例,并给出理由。
XXX的单价一定,购买XXX的数量和总价成正比例。
因为购买的数量和总价是随着单价的不变而相应变化的。
2.判断轮船行驶的速度与行驶的路程和时间是否成正比例,并给出理由。
轮船行驶的速度一定,行驶的路程和时间成正比例。
因为行驶的路程和时间是随着速度的不变而相应变化的。
3.判断每小时织布米数与织布的米数和时间是否成正比例,并给出理由。
每小时织布米数一定,织布的米数和时间成正比例。
因为织布的米数和时间是随着每小时织布米数的不变而相应变化的。
4.判断幼儿园老师分给每个小朋友的饼干的块数与小朋友的人数和所需的饼干数是否成正比例,并给出理由。
幼儿园老师分给每个小朋友的饼干的块数一定,小朋友的人数和所需的饼干数成正比例。
因为所需的饼干数是随着小朋友的人数的增加而相应增加的,而每个小朋友分得的饼干块数是不变的。
5.判断订阅《中国小年报》的份数与钱数是否成正比例,并给出理由。
订阅《中国小年报》的份数和钱数成正比例。
因为订阅的份数越多,需要支付的钱数也就越多。
6.判断XXX跳高的高度与他的身高是否成正比例,并给出理由。
XXX跳高的高度与他的身高成正比例。
因为身高越高,跳高的高度也就越高。
7.判断长方形的宽一定,它的面积与长是否成正比例,并给出理由。
长方形的宽一定,它的面积与长成正比例。
因为长方形的面积是由长和宽相乘得到的,而宽是不变的,所以面积随着长的增加而相应增加。
8.判断长方形的宽一定,它的周长与长是否成正比例,并给出理由。
长方形的宽一定,它的周长与长成正比例。
因为长方形的周长是由长和宽相加再乘以2得到的,而宽是不变的,所以周长随着长的增加而相应增加。
9.判断小麦的每公顷产量一定,小麦的公顷数与总产量是否成正比例,并给出理由。
小麦的每公顷产量一定,小麦的公顷数与总产量成正比例。
因为每公顷产量不变,所以总产量随着公顷数的增加而相应增加。
(完整版)小学六年级正比例、反比例练习题
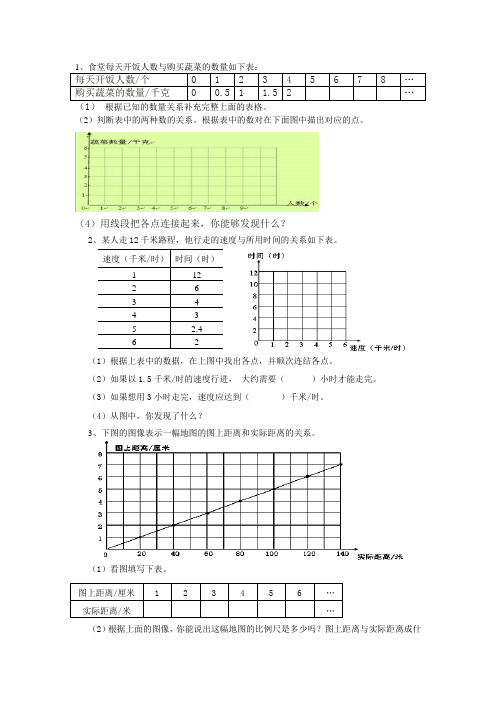
1、食堂每天开饭人数与购买蔬菜的数量如下表:
每天开饭人数/个
012345678…
购买蔬菜的数量/千克 0 0.5 1 1.5 2
…
(1) 根据已知的数量关系补充完整上面的表格。
(2)判断表中的两种数的关系。根据表中的数对在下面图中描出对应的点。
(4)用线段把各点连接起来,你能够发现什么?
2、某人走 12 千米路程,他行走的速度与所用时间的关系如下表。
强强到 A 地用了多长时间? (2)强强骑车 2.5 小时可以行多少千米? (3)按这样的速度行使 36 千米,强强需要多少时间?
6、同一时间,同一地点测得树高和影长如下图:
影பைடு நூலகம்/m
˙˙˙˙˙˙˙˙ 5.6
4.8 4.0 3.2 2.4 1.6 0.8 0
1 2 3 4 5 6 7 8 树高/m
(1)看图填写下表:
所行路程(km)
16
32
48
64
耗油量(L)
2
4
6
8
(1) 表中的耗油量与所行路程成正比 例吗?为什么?
14
12
(2) 右图是表示汽车所行路程与相应
10
耗油量关系的图像,说一说有什么
8
特点。
6
4
2
(3) 利用图像估计一下,汽车行驶 60km 0 的耗油量是多少?
耗油量(L)
路程(km)
8 16 24 32 40 48 56 64
9、给一间屋子铺地砖,每一块地砖的面积与所需地砖的块数如下:
每一块地砖面积/m2
0.16
0.4
0.5
……
需要地砖的块数/块
300
120
(1) 根据表中的数量关系,补充完整表格。
正比例的应用 小学数学 练习题

一、选择题1. 轿车和货车同时从A、B两地出发,相向而行,相遇时轿车行了全程的,那么轿车与货车的速度比是()。
A.7∶13B.6∶13C.7∶6D.6∶72. 豆芽的发芽率一定,发芽豆子的颗数与豆子总颗数()。
A.成正比例B.成反比例C.不成比例3. 在同一时刻,测得1米高的竹竿的影长为80厘米,教学楼的影长为16米。
则教学楼的高度为()米。
A.20 B.0.2 C.12.8 D.12804. 如图表示一辆汽车在高速公路上行驶的路程和耗油关系。
根据图像判断,行驶125千米耗油()升。
A.9 B.10 C.11 D.125. 下面图()表示的是成正比例关系的图象。
A.B.C.D.二、填空题6. 吴媛和施燕从学校同时出发到图书馆去,当吴媛走了一半时,施燕离图书馆还有786米,速度不变,吴媛到图书馆时,施燕还有全程的没走,学校到图书馆有( )米。
7. 小红买5个练习本需要4元钱,买10个同样的练习本需要( )元钱。
买练习本的本数和一共花的钱数成( )。
8. 100kg稻谷加工成大米是76kg。
照这样计算,加工380kg大米需要( )kg稻谷。
9. 如果X和Y成正比例,那么“?”填_____,如果X和Y成反比例,那么“?”填_____。
X 4Y 80 10010. 一种合金是由铝和铁按7:3加工而成,现有铝280千克,要加工成这种合金,需要铁千克;如果要加工这种合金600千克,需要铝千克.三、解答题11. 李明把几根长短不同的竹竿直立在操场上,在同一时间里测量这几根竹竿的长度和相应的影长,情况如下表:竹竿长/米 1 1.2 1.8 2 4 5影长/米0.5 0.6 0.9 1 2 2.5比值(1)算出竹竿长与影长的比值,填在表格中。
(2)通过测量和计算,你发现了什么?(3)操场上的旗杆高度为10米,你能求出此时旗杆的影长是多少米吗?(4)这时王刚测出操场旁一棵松树的影长是2.4米,你能算出这棵松树的实际高度吗?12. 400千克小麦可以磨面粉340千克,照这样计算,700吨小麦可以磨面粉多少吨?(用比例知识解答。
人教版六年级下册数学用正比例解决问题(附答案)

人教版六年级下册数学用正比例解决问题一.解比例。
51=25x x 2=5.311.2 32=15x x 5.2=4.01二、填空1.车轮直径一定,所行的路程和车轮的转数成( )比例。
2.因为每度电的价格一定,所以电费和用电的度数成( )比例。
3. 把下面的数量关系式补充完整路程÷( )=时间 路程÷( )=速度总价÷( )=数量 总价÷ ( )=单价 三、判断1.两种相关联的量,不成正比例,就成反比例。
( )2.图上距离和实际距离成正比例。
( )3.X 和Y 表示两种变化的相关联的量,同时5X -7Y =0,X 和Y 不成比例。
( )4.分数的大小一定,它的分子和分母成正比例。
( )5.在一定的距离内,车轮周长和它转动的圈数成反比例。
( ) 四、解决问题 1.2.小明买9本练习本花了4.5元,如果买同样的练习本20本需要付多少元?3.小明买9本练习本花了4.5元,如果用20元钱买同样的练习本,可以买多少本?4.运一批煤,18次运了90吨,照这样计算,14次可以运多少吨?5.运一批煤,18次运了90吨,照这样计算,多少次才能运完140吨煤?6.用8辆卡车每天可运货128吨,照这样计算,用同样的卡车11辆,每天可运货多少吨?7.一种水管,40米重60千克。
现称得一捆水管重270千克,这捆水管共长多少米?8.华南服装厂3天加工西装180套,照这样计算,要生产540套西装,需要多少天?9.王师傅生产25个零件需要1.5小时,照这样计算,生产125个零件需要多少小时?10.把一根3m长的标杆直立在地上,测得影长2.7m,同时测得旁边一棵树的影长比标杆影长多3.6m,这棵树高多少米?11.一辆汽车2小时行驶140千米,照这样的速度,从甲地到乙地的距离是400千米,需要行驶多少小时?12.一个修路队,原计划每天修400m,15天可以修完。
结果12天就完成任务,实际每天修多少米?参考答案:人教版六年级下册数学用正比例解决问题一.解比例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基础练习
1、判断下面每题中的两种量成什么比例关系?
1)、打字速度一定,打字的总数量和时间;
2)、三角形的面积一定,底和高;
3)、x=3y x和y
4)、每块砖的面积一定,砖的块数和总面积;
5)、速度一定,路程和时间。
综合练习
1、一辆汽车2小时行驶140千米,照这样的速度,从甲地到乙地共行驶5小时,甲乙两地之间的公路长多少千米?
2、一辆汽车2小时行驶140千米,照这样的速度,甲乙两地之间的公路长350千米,从甲地到乙地需要行驶多少小时?
3、小丽想知道一大捆铁丝的长度,从中截取了5m长的一段,测得其质量为400g。
现称得这捆铁丝的质量为6kg。
这捆铁丝长多少米?
4、小梁在旗杆旁立一根2米高的竹竿,量得竹竿影长为1.2米。
在同时同地,测得旗杆的影长是
6.6米。
求旗杆实际长几米?
发展练习
1、先想一想:下面各题中存在着什么比例关系?再填上条件和问题,并用比例知识解答。
①李明5天看了240页故事书,照这样计算,____ ___?
②王师傅4小时生产了200个零件,________ ,________ ?
2、、一辆汽车从甲地出发去乙地,2小时行驶140千米,照这样的速度,这辆汽车又行驶3小时到达乙地,甲乙两地之间的相距多少千米?。
