圆柱绕流的一种网格画法
圆柱绕流的一种网格画法
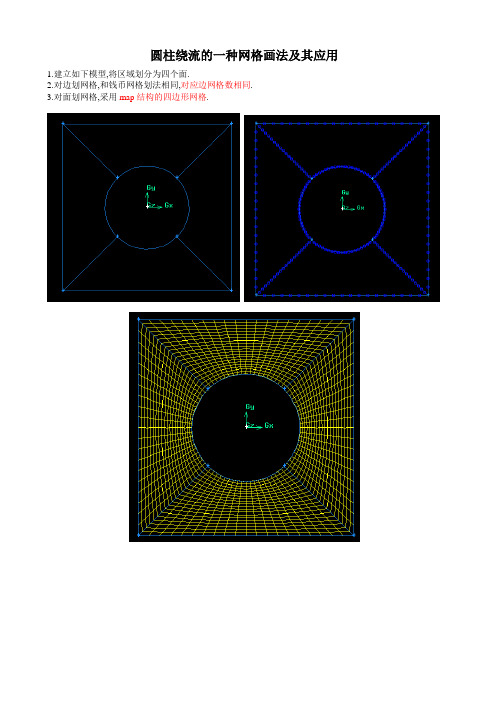
圆柱绕流的一种网格画法及其应用
1.建立如下模型,将区域划分为四个面.
2.对边划网格,和钱币网格划法相同,对应边网格数相同.
3.对面划网格,采用map结构的四边形网格.
应用
1.在gambit中建立如下模型
2.建立两个面将模型分为四部分.
3.对两边圆弧结构划网格,对应边网格数相同,采用map结构的四边形网格,对体采用cooper方式划网格.如下图所示.
4.对圆柱形区域划网格,先处理,建立如下图所示四个面,将两个体分为8个体,采用上面圆柱绕流网格划法对面划网格,采用cooper方式对体划网格.
5.对于每个已经化为4个体的圆柱形区域,选中四个体直接进行网格划分。
(Hex-Map)。
FLUENT动网格-圆柱体在管道内运动模拟
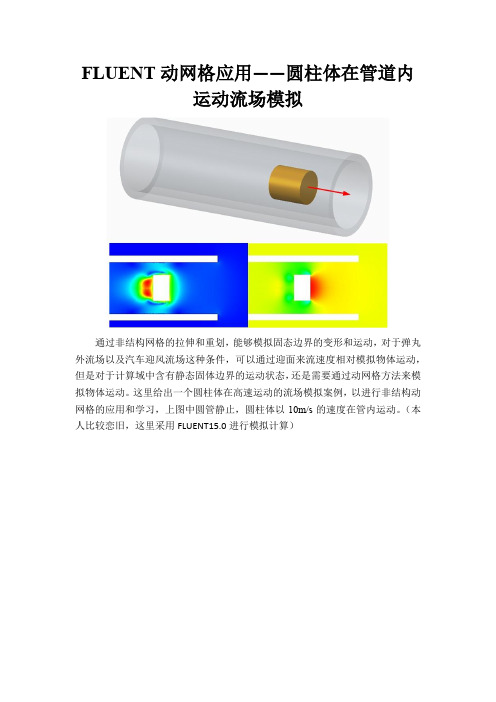
FLUENT动网格应用——圆柱体在管道内
运动流场模拟
通过非结构网格的拉伸和重划,能够模拟固态边界的变形和运动,对于弹丸外流场以及汽车迎风流场这种条件,可以通过迎面来流速度相对模拟物体运动,但是对于计算域中含有静态固体边界的运动状态,还是需要通过动网格方法来模拟物体运动。
这里给出一个圆柱体在高速运动的流场模拟案例,以进行非结构动网格的应用和学习,上图中圆管静止,圆柱体以10m/s的速度在管内运动。
(本人比较恋旧,这里采用FLUENT15.0进行模拟计算)。
三维圆柱扰流-卡门涡街数值仿真方法--详细教程

时间长
时间步长的选取决定能否快速观察到卡门涡街,卡 门涡街在Re>45时出现,根据斯特劳哈尔数(St)算 出涡的脱落频率(fs),求出脱落周期,然后根据 经验公式,取脱落周期的1/75作为时间步长。
斯特劳哈尔数公式 St fsD / U
仿真分析 Re=10 时的速度云图
流线对涡结构
Re=50压力云图
速度云图 此时出现涡街
Re=50 观测升 力震荡
残差线震荡
Re=100
Re=100000
Re=100000 残差与升力检测
Re=10 Re=100
Re=50 Re=100000
阻力系数
Re
Cd
10
2.24
50
1.83
100
1.67
100000
1.05
CFX三维圆柱扰流分析 —卡门涡街模拟
分析过程
1.建模与网格划分 2.参数设置 3.结果与分析
几何模型
建立如图所示的几何模型,给各面按图所示命名。圆 柱的长为0.3,直径0.1,圆柱圆心到INLET和TOP, DOWN的距离为0.5,距离OUTLET为2
3D网格
按左图切分 BLOCK
按左图布点, Z方向10等分
网格总数100000 Quality 0.85
圆柱周边网格
边界条件设置
Inlet、Top、Down: velocity inlet(速度值以Re决定) Body:wall no slip Outlet:opening Side、Sym: symmery 非定常仿真 湍流模型:层流(Re<300)、大涡模拟(Re>300) 流体属性:空气(不可压)
圆柱绕流问题的三种网格划分

中山大学工学院计算流体力学实验报告实验名称:圆柱绕流问题的三种网格划分姓名:刘广参与组员:刘广学号:11309018任课教师:詹杰民学科专业:工学院理论与应用力学中山大学2014年04月05日图1对于四个面,如图2所示,参数interval count我们选择10,点击apply效果如图3所示。
图2Page 3 of 12图3下面我们对其划分的网格进行质量分析。
点击面板进入网格分析区域,就是Examine Mesh面板当中,Display Type我们选择Rang,2D Element,三角形网格类型,点击下方update 就可以看到如图4所示网格质量图。
图4Page 4 of 12我们继续看图5所示的网格质量分析数据,可以看到,三角形网格一共有1324个,其中在圆柱后方的若干区域网格质量最差。
图5最差质量的网格如图6所示。
图6接下来我们开始介绍矩形网格划分。
如下图7所示;我们首先画四段四分之一圆弧,其中圆弧对应的圆周半径为1.然后我们再绘制如图所示的矩形。
其中外部的矩形长32,宽22,并做如下图所示的划分。
其中详细作图步骤在上次实验报告中有详细叙述,这里不再赘述。
所示图7中有八个面,其中圆形上的点为对圆形进行45度划分。
现在我们选择矩形网格对Page 5 of 12其进行划分,图7对于八个面,如图8所示,参数interval count我们选择10,点击apply效果如图9所示。
图8Page 6 of 12图9下面我们对其划分的网格进行质量分析。
点击面板进入网格分析区域,就是Examine Mesh面板当中,Display Type我们选择Rang,2D Element,矩形网格类型,点击下方update就可以看到如图10所示网格质量图。
图10我们继续看图11所示的网格质量分析数据,可以看到,矩形网格一共有20000个,其中在Page 7 of 12圆柱上方、左方、右方、后方的若干区域网格质量最差。
圆柱绕流

二维圆柱绕流摘要:采用有限体积法求解二维N -S 方程,对雷诺数1,10,100的二维圆柱非定常流场进行了数值模拟,对比各雷诺数下其流动情况发现,在Re=1时,圆柱上下游的流线前后对称,此Re 数范围的绕流称为斯托克斯区;随着Re 的增大,圆柱上下游的流线逐渐失去对称性。
当Re=10时,沿圆柱表面流动的流体在到达圆柱顶点(90度)附近就离开了壁面,分离后的流体在圆柱下游形成一对固定不动的对称漩涡(附着涡),涡内流体自成封闭回路而成为“死水区”;随着Re 的增大,死水区逐渐拉长圆柱前后流场的非对称性逐渐明显,此Re 数范围称为对称尾流区。
圆柱下游流场不再是定常的,圆柱后缘上下两侧有涡周期性地轮流脱落,形成规则排列的涡阵,这种涡阵称为卡门涡街。
1. 圆柱绕流研究圆柱绕流是一个经典的流体力学问题,流体绕圆柱体流动时,过流断面收缩,流速沿程增加,压强沿程减小,由于粘性力的存在,,就会在柱体周围发生边界层的分离,形成圆柱绕流。
圆柱绕流现象比较复杂,因此,对圆柱绕流研究具有重要的基础理论意义。
研究圆柱绕流问题在工程实际中也具有非常重要的意义。
如水流对桥梁、海上钻井平台支柱、海上输运管线、桩基码头等的作用中,风对塔设备、化工塔设备,高空电缆等的作用中,都有着重要的工程应用背景。
因此,对圆柱绕流进行深入研究,对其流动机理进行分析,不仅具有理论意义,还有明显的社会经济效益。
2. 数值方法因为本文主要求解雷诺数Re=1,10,100时的圆柱绕流情况,需要求解二维非定常不可压的N—S 方程组:本文采用有限体积法对上述微分方程进行离散,然后用SIMPLE 算法对离散方程进行求解,计算中时间推进采用二阶隐式格式,空间离散采用三阶精度的QUICK 格式。
控制方程如下:0jju x ∂=∂ (1) 1()()ji j i j j j ju u p u u t x u x x νρ∂∂∂∂∂+=-+∂∂∂∂∂ (2) 3. 网格划分及模拟工况3.1计算网格计算的区域大小为上游边界距圆柱圆心为2.5D ,下游边界距圆柱圆心10D ,顶部和底部边界距圆柱圆心2.5D ,如图1所示。
4.4 圆柱绕流(10)

4.4圆柱绕流钝体绕流是流体力学领域内的经典问题,人们之所以对其研究的热情经久不衰,一是由于其中很多重要的流动机理至今仍不清楚,二是其广泛应用于许多工程当中,如能源工程、水利工程和船舶工程等。
因此对钝体绕流进行研究,不仅具有重要的理论意义,而且具有广泛的工程应用价值。
4.4.1基本理论与物理模型对于不可压缩粘性流体,在直角坐标系下,其运动规律可用Navier-Stokes 方程来描述,连续性方程和动量方程分别为:0jjU X ∂=∂ (4-4-1)()1()X j i i i j i j jU U U U P v t X X X ρ∂∂∂∂∂+=-+∂∂∂∂∂ (4-4-2)计算区域如图4-4-1所示(单位:mm )图4-4-1 计算区域示意图4.4.2在Gambit 中建立模型Step1:启动Gambit 并选择求解器为Fluent5/6。
Step2:创建节点 操作:→→打开对话框如图4-4-2所示,在对话框中输入各各节点的x 、y 坐标值,各坐标分别为(0,0,0)、(1,0,0)、(1,0.2,0)、(0,0.2,0)、(0.2,0.1,0)、(0.18,0.1,0)和(0.2,0.08,0),此时图形如图4-4-3所示。
图4-4-2 创建点对话框图4-4-3 创建的点示意图Step3:由节点创建线(1)创建直线操作:→→打开对话框如图4-4-4所示,Shift+鼠标左键依次点击计算区域外围四个点,点击Apply 确认。
图4-4-4 创建直线对话框图4-4-5 创建圆对话框(2)创建中间圆操作:→→打开对话框如图4-4-5所示,在Method中选择过圆心和两点画圆,在Center中选择圆心,在End-Points中选择另外两点。
Step4:由边线创建面操作:→→打开创建面对话框如图4-4-6所示,Shift+鼠标左键依次点击计算区域外围边线上的各条线段。
点击Apply确认。
同样的,可创建中间圆面。
圆柱绕流的算例

二、Fluent计算圆柱绕流算例
用PIV方法,我们通过实验得到了圆柱后面卡门涡街流场的信息,现在,我们通过Fluent来计算相同条件下的圆柱绕流。
选择一个长15cm,宽12cm的矩形区域作为计算区域,中间有一个直径为2cm的圆柱,左端定义为速度边界,来流速度为6.25cm/s(这样可以保证圆柱上下两侧的速度平均值为7.5cm/s,与PIV实验的条件一致),右端是出口边界,其它边界为固壁。
在二维条件下计算这个绕流问题(Re=1393)。
图2-4-3显示了上述计算区域和边界条件。
图2-4-3 二维圆柱绕流的计算区域和来流条件
在gambit当中进行网格划分,在圆柱边界附近,网格非常密,图2-4-4显示了靠近圆柱附近的部分网格:
图2-4-4圆柱附近的网格
在Fluent中进行计算,相关参数分别选择如下表:
计算之后,我们得到了圆柱绕流的尾迹,它的流线图以及涡量分布图分别图2-4-5(a, b)所示:
从上述涡量分布可以看出,在圆柱下游,也有两条辫子一样形状的涡量层,在下游稍微远端交替甩动。
比较PIV方法得到的照片,我们也看到了这样的两个辫子一样的涡量层,其分布位置与计算所得的结论是一致的。
比较这个时刻的流线图也可以看出来,它们的流线分布
也基本是一致的。
这说明,PIV方法是可靠的。
二维圆柱绕流

二维圆柱绕流问题问题描述:将三维的悬空管道涡激振动问题简化为二维的圆柱绕流问题,描述其漩涡的脱落以及圆柱面的压力情况变化,流场的分布,为三维的模拟进行准备。
1.不考虑海底影响,考虑重力加速度,海面对称边界,网格采用4边形网格。
流速为0.2m/s ,圆柱直径D 为0.245m ,高10m ,长12m ,圆柱距离outflow 出口为10m ,距离海底为5m 。
模型如下图1所示:图1 不考虑海底的模型尺寸图采用标准的εk -湍流模型,湍流强度I 采用下式求得:0415.0)(16.0Re 16.0125.0125.0=⨯⨯=⨯=--vd u I 水力直径D=0.245。
圆柱处的升力曲线如图2所示,阻力曲线如图3所示。
压力云图,速度云图和涡量云图分别为图4、5、6所示。
图2 升力曲线图3 阻力曲线图4 压力云图图5 速度云图图6 涡量云图2.不考虑海底,不考虑重力加速度,海面对称边界,采用4边形网格。
不考虑重力,其他设置一样,升力曲线,阻力曲线如图7、8所示。
压力云图、速度云图和涡量云图如图9、10、11所示。
结论:如果不加重力的话,是不对的。
3.考虑海底(圆柱中心离海底为1m),海面对称边界,4边形网格。
流速为0.2m/s,圆柱直径D为0.245m,高10m,长12m,圆柱中心距离outflow出口为10m,距离海底为1m。
模型尺寸如图12:图12 模型尺寸图4.考虑海底(圆柱中心离海底为1m),海面墙壁边界,4边形网格。
5.考虑海底(圆柱中心离海底为0.5m),海面墙壁边界,4边形网格。
总结:由于间隙的减小,脱曳力系数和升力系数都相应的增加,管道所受外力增加,且由于升力的增加,使得管道在竖直方向上的位移减小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱绕流的一种网格画法及其应用
1.建立如下模型,将区域划分为四个面.
2.对边划网格,和钱币网格划法相同,对应边网格数相同.
3.对面划网格,采用map结构的四边形网格.
应用
1.在gambit中建立如下模型
2.建立两个面将模型分为四部分.
3.对两边圆弧结构划网格,对应边网格数相同,采用map结构的四边形网格,对体采用cooper方式划网格.如下图所示.
4.对圆柱形区域划网格,先处理,建立如下图所示四个面,将两个体分为8个体,采用上面圆柱绕流网格划法对面划网格,采用cooper方式对体划网格.
5.对于每个已经化为4个体的圆柱形区域,选中四个体直接进行网格划分。
(Hex-Map)。
