机械原理第三章作业答案
机械原理 课后习题答案
⎛ ⎜ ⎝
m / s2 mm
⎞ ⎟ ⎠
作加速度图
C
2
3
D
B
p(d) 4
(c3)
b2 (b1) (b3)
题3-8 c) 解(续2)
[解]
（3）加速度分析 aB 2 (= aB1) → aB3 → aC 3
1) 求aB2
A 1 ω1
2) 求aB3
aB3
=
an B3D
+
at B3D
=
aB
2
+
ak B3B2
得d点
p(c3)
E
vD = μv pd = 0.005 × 44.6 = 0.223 (m / s)
作 de ⊥ bc2
并使
de = DE = lDE = 40 bd BD lBD 50
得e点
vE = μv pe = 0.005 × 32.0 = 0.16 (m / s)
3) 求ω2
ω2
=
vC 2B lBC
p' = 2p'l + p'h − 3n' = 2 × 3 + 0 − 3× 2 = 0
p' = 2p'l + p'h − 3n' = 2 ×10 + 0 − 3×6 = 2
F = 3n − (2pl + ph − p') − F' = 3 × 11 − (2 × 17 + 0 − 2) − 0 =1
P24
B P23
3
2A
P12
1
4
D
P14
vE
=
vB
P13 E P13B
机械原理课后答案第三章作业
e L1 eiθ 1 + L2 eiθ 2 = s3 ei•0 + ei•2
(*)
按欧拉公式展开：100(cosθ1+isinθ1)+ 300 (cosθ2+isinθ2) = s3 + 30i
分离虚、实部：100 cos60 ° + 300cosθ2= s3 (1)
100 sin60 ° + 300sinθ2=30 (2)
= ω3 μL P13E = 2.56×3 ×46.5/1000 =0.357（m/s）
3）当VC =0时， ψ角之值（有两解）。
解：作出VC =0时机 构的两个位置，即 AB与BC共线的两 个位置，如图c。量 出：
ψ1=26.4 ° ψ2=226.6 °
3-14 在图示的机构中，已知原动件1以等速度ω1=10rad/s逆时针方 向转动，lAB=100mm，lBC=300mm，e=30mm。当θ1=60°时，试 用复数法求构件2的角位移θ2、角速度ω2及构件3的速度V3。
由（2）式解得：sinθ2= －0.1887
θ2=349.12 °
对（*）式求导： (
•
L1θ 1
)
i eiθ 1
+(
•
L2 θ 2
)
i
eiθ
2
=
•
s3 +0
欧拉公式展开：L1θ•1i (cosθ1+isinθ1)+
•
L2 θi(2cosθ2+isinθ2) =
•
s3
分离虚、实部： - 100sin60 °θ•1 - 300 sinθ2
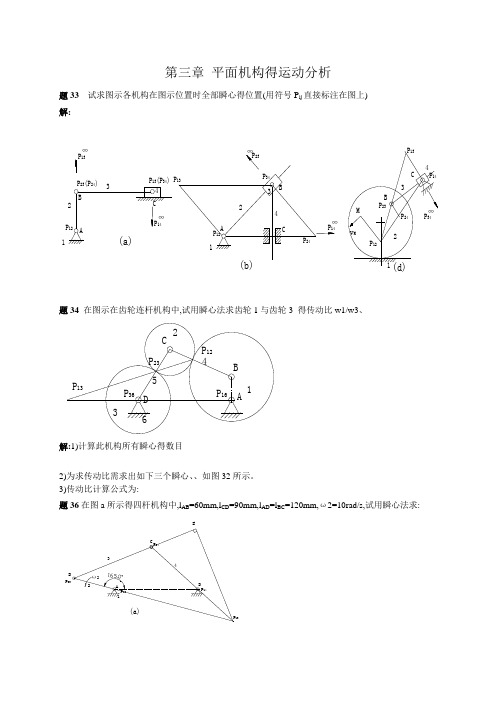
3-1 试求图示各机构在图示位置时的全部瞬心（用符号Pij 直接标注在图上）。
西北工业大学机械原理课后答案第3章-1
解法一:
速度分析:先确定构件3得绝对瞬心P36,利用瞬心多边形,如图(b)
由构件3、5、6组成得三角形中,瞬心P36、P35、P56必在一条直线上,由构件3、4、6组成得三角形中,瞬心P36、P34、P46也必在一条直线上,二直线得交点即为绝对瞬心P36。
第三章平面机构得运动分析
题33试求图示各机构在图示位置时全部瞬心得位置(用符号Pij直接标注在图上)
解:
题34在图示在齿轮连杆机构中,试用瞬心法求齿轮1与齿轮3得传动比w1/w3、
解:1)计算此机构所有瞬心得数目
2)为求传动比需求出如下三个瞬心、、如图32所示。
3)传动比计算公式为:
题36在图a所示得四杆机构中,lAB=60mm,lCD=90mm,lAD=lBC=120mm,ω2=10rad/s,试用瞬心法求:
解:1)速度分析:
以F为重合点(F1、F5、、F4)有速度方程:
以比例尺速度多边形如图37 (b),由速度影像法求出VB、VD
2)加速度分析:以比例尺
有加速度方程:由加速度影像法求出aB、aD
题316在图示得凸轮机构中,已知凸抡1以等角速度转动,凸轮为一偏心圆,其半径,试用图解法求构件2得角速度与角加速度。
4)当时,P13与C点重合,即AB与BC共线有两个位置。作出得两个位置。
量得
题312在图示得各机构中,设已知各构件得尺寸、原动件1以等角速度ω1顺时针方向转动。试用图解法求机构在图示位置时构件3上C点得速度及加速度。
解:a)速度方程:
加速度方程:
b)速度方程:
加速度方程:
c)速度方程:
加速度方程:
题314在图示得摇块机构中,已知lAB=30mm,lAC=100mm,lBD=50mm,lDE=40mm。曲柄以等角速度ω1=10rad/s回转,试用图解法求机构在φ1=45°位置时,点D与点E得速度与加速度,以及构件2得角速度与角加速度。
西北工业大学机械原理课后答案第3章
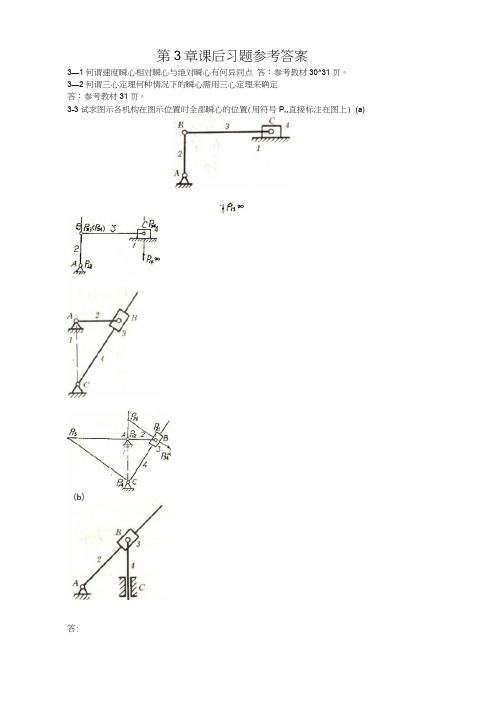
第3章课后习题参考答案3—1何谓速度瞬心相对瞬心与绝对瞬心有何异同点答：参考教材30^31页。
3—2何谓三心定理何种情况下的瞬心需用三心定理来确定答：参考教材31页。
3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P,,直接标注在图上) (a)答:3-4标出图示的齿轮一连杆纽合机构中所有瞬心，并用瞬心法求齿轮1与齿轮3的传动比U)l/U)3o答：1)瞬新的数目：K 二N (N-1 )/2=6 (6T )/2=152）为求3（/33需求3个瞬心％、P%、P 竹的位置由构件J 3在K 点的速度方向相同，可知4与3同向。
3-6 在图示的四杆机构中，L AB 二60mm, LcD=90mm, L AD =L BC = 120mm, u)2=10rad/s,试用瞬心法求：1) 当 0=165°2) 当 0=165°2)求vc 定出瞬心"2的位置(图b) 因M 为构件3的绝对瞬心，则有 U )3=VB /IB PI 3=W2I JB / U=10X X78=(rad/s) v c = u c pi3U)a=X52X = (m/s)（2分）时，点的速度vc;吋，构件3的BC 线上速度最小的一点E 的位置及速度的大小:3i/3s= PadPu/PidPi^DK/AK(图b)C线上速度灵小的点必与p13点的距离3—11速度多边形和加速度多边彤有哪些特性试标出图中的方向。
答速度多边形和加速慶多边形特性参见下图，各速度方向在图中用箭头标出。
3T2在图示的机构中，设已知构件的尺寸及原动件1的角速度（顺时针），试用图解法求机构在图示位置吋C点的速厦和加速度。
V C3=V B+V C3B=V C2+V C3C2（2 分）aC3=aB+a n C3B+a C38=aC2+a C3C2+a”C3C2Vc2=0 3C2=0 （2 分）Vc30=O U） 3=0 a k C3C2=0（1分）（1分）答:（3分）答:（2分）V C2=V B+V C28=V O3+V G2C3U)3=W 2=0（2分）（2分）（1分）& f t k ra^+a C2B+3 C2B~3C3+3 C2C3+3 C2C3（3分）(c)(bj s bi iV B3=V B2B3B2（2分）（1分） a 阴+a B3_aB2+a B3B2+a B3B2 3- 13试判斷在图示的两机构中.B 点足否都存在哥氏加速度又在何位置哥氏加速度为零忤 出相应的机构位置图。
《机械原理》(于靖军版)第3章习题答案
3-2 计算题图3-1所示各机构（或运动链）的自由度。
并判断其中是否含有复合铰链、局部自由度或虚约束？如有，请指出。
(b)(d)(g)题图3-1答：（a ）064===H L p ,p ,n ，0624323=⨯-⨯=-=L p n F 。
因为 0=F ，所以不能成为机构。
（b ）143===H L p ,p ,n ，01423323=-⨯-⨯=--=H L p p n F 。
因为0=F ，所以不能成为机构。
（c ）032===H L p ,p ,n ，0322323=⨯-⨯=-=L p n F 。
因为0=F ，所以不能成为机构。
（d ）01410===H L p ,p ,n ，214210323=⨯-⨯=-=L p n F 。
因为 2F ==原动件数，所以能成为机构。
（e ）075===H L p ,p ,n ，123=--=H L p p n F 。
D 处有一个复合铰链。
（f ）186===H L p ,p ,n ， 32362811L H F n p p =--=⨯-⨯-=，I 处有一个局部自由度；B 或C 处的移动副为虚约束；I 处的两个高副之一为虚约束。
（g ） 滚子B 和M 为局部自由度，没有复合铰链和虚约束，因此9=n ，12=L P ，2=H P ，于是该运动链的自由度为：121229323=-⨯-⨯=--=H L P P n F 。
由于该运动链的自由度等于原动件数目，因此具有确定的运动。
3-3 题图3-2所示为一回转式三缸内燃发动机的机构简图。
其中A 、B 、C 处三个活塞，它们依次点火推动从动件绕O 2转动。
（1） 计算机构的自由度。
并指出存在的复合铰链、局部自由度或冗余约束。
（2） 说明该发动机是由哪种四杆机构组成的。
题图3-2解：机构的自由度为1。
O 1处有复合铰链。
曲柄滑块机构。
无局部自由度和冗余约束。
注：O 1O 2有一个杆。
3-6 试计算题图3-4所示两种8杆机构的自由度，并进行ADAMS 模型运动仿真。
机械原理课后习题答案
《机械原理》课后习题答案第2章（P27）2-2 计算下列机构的自由度，如遇有复合铰链、局部自由度、虚约束等加以说明。
（a）n=3，p l=3 F=3*3-2*3=3（b）n=3，p l=3，p h=2 F=3*3-2*3-2=1 （B处有局部自由度）（c）n=7，p l=10 F=3*7-2*10=1（d）n=4，p l=4，p h=2 F=3*4-2*4-2=2 （A处有复合铰链）（e）n=3，p l=4 F=3*3-2*4=1 （A或D处有虚约束）（f）n=3，p l=4 F=3*3-2*4=1 （构件4和转动副E、F引入虚约束）（g）n=3，p l=5 F=(3-1)*3-(2-1)*5=1 （有公共约束）（h）n=9，p l=12，p h=2 F=3*9-2*12-2=1 （M处有复合铰链，C处有局部自由度）2-3 计算下列机构的自由度，拆杆组并确定机构的级别。
（a）n=5，p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组，故此机构为Ⅱ级机构。
（b）n=5，p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。
（c）n=5，p l=7 F=3*5-2*7=1拆分时只须将主动件拆下，其它构件组成一个Ⅲ级杆组，故此机构为Ⅲ级机构。
2-4 验算下列运动链的运动是否确定，并提出具有确定运动的修改方案。
（a）n=3，p l=4，p h=1 F=3*3-2*4-1=0 该运动链不能运动。
修改方案如下图所示：（b）n=4，p l=6 F=3*4-2*6=0 该运动链不能运动。
修改方案如下图所示：或第3章（P42）3-2 下列机构中，已知机构尺寸，求在图示位置时的所有瞬心。
（a）（b）（c）(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中，三个圆互作纯滚，试利用相对瞬心P13来讨论轮1与轮3的传动比i13。
第5章（P80）5-2 一铰接四杆机构（2）机构的两极限位置如下图：（3）传动角最大和最小位置如下图：5-3题略解：若使其成为曲柄摇杆机构，则最短杆必为连架杆，即a 为最短杆。
西北工业大学机械原理课后答案第3章
O OO OP 2P 3F 23(P 24Pl 3(P 34)(a)(b)Pl 3Pl 6A 1题3-6在图a 所示的四杆机构中,第三章平面机构的运动分析题3-3试求图示各机构在图示位置时全部瞬心的位置（用符号P j 直接标注在图上）解：题3-4在图示在齿轮-连杆机构中，试用瞬心法求齿轮1与齿轮3的传动比w1/w3.C 2P 12P 23St -解：1）计算此机构所有瞬心的数目K N （N1）2152） 为求传动比 < 3需求出如下三个瞬心 R 6、P 36、P 13如图3-2所示。
; 1 巳6只33） 传动比 仁3计算公式为： —3P 16P 13I AB =60mm , l cD =90mm , l AD =|Bc =120mm , w 2=10rad/s ，试用瞬心P134 C 4L CP 12AM B3P iP 34CBMF 24F 34P ?4(d)Pl 4法求:V B3I AB2IAB lBPI32.56rad sV ClCR 3 3 0.4m s量得 1 26.42 226.6P 3434B P 233 22A ,D- i Pl4P 12 1(a)P 131） 当0 =165。
时，点C 的速度Vc ;2） 当$ =165。
时，构件3的BC 线上速度最小的一点 E 的位置及速度的大小; 3） 当Vc=O 时，0角之值（有两个解）解：1）以选定比例尺，绘制机构运动简图。
（图3-3 ）2）求V c ，定出瞬心P 13的位置。
如图 3-3 （a ）3）定出构件3的BC 线上速度最小的点 E 的位置。
因为BC 线上速度最小的点必与 P 13点的距离最近，所以过 P 13点引BC 线延长线的垂线交于 E 点。
如图3-3 （a ）v E1ER 3 3 0.375ms4）当V C 0时，P 13与C 点重合，即AB 与BC 共线有两个位置。
作出 V C 0的两个位置。
题3-12在图示的各机构中，设已知各构件的尺寸、原动件 1以等角速度3 1顺时针方向转动。
机械原理第三章作业答案
P13
2（C）、既然机构中各构件与其速度图和加速度图之间均存在影像关系， 因此整个机构与其速度和加速度图之间也存在影像关系，对吗？
答：不对
速度、加速度影像原理只适用于同一构件上的点求速度 和加速度，不适用于整个机构。
3（C）、当用速度瞬心法和用速度影像法求同一构件（如图所示机构连杆3 上）上任意一点P的速度时它们的求解条件有何不同？各有何特点？
B
3（C）、图示机构中，已知 lAC lBC lCD lCE lDF lEF 20mm ，
滑块1及2分别以匀速且 v1 v2 0.002 m / s 做反向移动，试求机构在
位置时的速度大小之比 vF v1
解：对C点进行速度分析 建立方程为
。
1 v1 A
7
3 30°
C
D
6
F
4
① VC VA VCA VB VCB
B
2
v2
5
E
b
p
60
a°
d c
e
vF f v1
pf
3 pc
3
pa pa
3
pc 3 pa
pf 3pc 3 3 pa
3-9、试判断在图示的两机构所在位置中，B点是否都存在 哥氏加速度？。并思考下列问题：
1）、在什么条件下才存在哥氏加速度？
答：用速度瞬心法求构件（如3）上任意
P
点（如P）速度时需找出相关的瞬心；
而用速度影像法求点速度时，需先在
速度多边形中求出同一构件（如3）
上任意两点（如B、C两点）的速度。
瞬心法较简便，但有时瞬心不怎好求；影像法只对同一 构件上的点适用，不适用于整个机构。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
k = 2ω V aB2B3 3 B2B3
b
精品课件！
精品课件！
答：不对 速度、加速度影像原理只适用于同一构件上的点求速度 和加速度，不适用于整个机构。
3（C）、当用速度瞬心法和用速度影像法求同一构件（如图所示机构连杆3 上）上任意一点P的速度时它们的求解条件有何不同？各有何特点？
答： 用速度瞬心法求构件（如3）上任意 点（如P）速度时需找出相关的瞬心； 而用速度影像法求点速度时，需先在 速度多边形中求出同一构件（如3） 上任意两点（如B、C两点）的速度。
vF 位置时的速度大小之比 v1
解：对C点进行速度分析 建立方程为
。
1
A
7
v1
3 30° 4
D
6
C
5
F
①
VC VA VCA VB VCB
b d c e
B
2
v2
E
p a
60 °
vF pf 3 pc 3 3 f v1 pa pa
pc 3 pa pf 3 pc 3 3 pa
P21
P14
答： 求出2、4的瞬心P24，根据其在瞬心P21、P14连 线上的位置可迅速求得4与2转向相同。 求出3、1的瞬心P31 （绝对瞬心），由
VB AB 2
P13
VB 3 BP31
E
P24 P21 P14
VE 3 EP 31
P13
2（C）、既然机构中各构件与其速度图和加速度图之间均存在影像关系， 因此整个机构与其速度和加速度图之间也存在影像关系，对吗？
P12 P13 1
P23 B 2 C
P14
A
1
4 P23
3 V3 = 1P14 P12
B
3（C）、图示机构中，已知 l AC lBC lCD lCE lDF lEF 20mm ， 滑块1及2分别以匀速且 v1 v2 0.002m / s 做反向移动，试求机构在
P24 P21 4 2 P24 P 14
或 B2,
VB3=VB2 + VB3B2
VB2=VB3 + VB2B3
p
b3 b2
ω=ω
3
2
r aB3 = aB2 + ak + a B3B2 B3B2
哥氏加速度不 为零
k = 2ω V aB3B2 2 B3B2
r aB2 = aB3 + ak + a B2B3 B2B3
1（A)、速度瞬心是指两个构件相对运动时相对速度相等的点（ ）。
2（C)、平面机构中任一构件的瞬时运动均可视为绕其绝对速度瞬心定 轴转动，故构件上任一点的加速度等于绕该速度瞬心转动的法相和切向 加速度矢量之和（ ）。 E
P24 简答题(5分）：
1（B)、简要说明如图所示的机构，如何用瞬心法迅速地确定构件4 的转向及 构件3上任一点的速度大小和方向？（原动件为2，转速、转向已知）
因ω2总为零，所以不 仅机构在图示位置无 哥氏加速度,且机构在 任意位置处都无哥氏 加速度。
（ 3）、在图示位置，从数值上说 aB2 B3 22VB2 B3 ，但从概念
k
k a 上说 B 2 B3 22VB 2 B3 是错误的。
b
P24
P21
P14
2 P 24 P 21 4 P 24 P 14
3-9、试判断在图示的两机构所在位置中，B点是否都存在 哥氏加速度？。并思考下列问题：
1）、在什么条件下才存在哥氏加速度？ 2）、根据上一条，请检查一下所有哥氏加速度为零的位 置是否已全部找出？
k a 3)、在图a中， B 2 B3 22VB 2 B3 ，对吗？为什么？
2
A1
3
B(BB 1,B 2 2,B3) ,
B
B
C
(a)
(b)
B1
解（1）、当 ω 、Vr 中之一等于零时，B点的哥氏加 速度 为零 1
2 Vr 0
2
ω1
b
（2） （a)图 Ⅰ Ⅲ Ⅰ V
B(B1, B2, B3)
B(B1, B2, B3)
Ⅱ
B(B1, B2, B3)
B(B1, B2, B3)
VB3B2 = VB2B3=0
ω2 = ω 3=0 b
P
瞬心法较简便，但有时瞬心不怎好求；影像法只对同一 构件上的点适用，不适用于整个机构。
计算、分析、作图题（每题13分）
1（A）、试求图示机构在图示位置时全部瞬心
P13 P23 P24 P12
P14
P34
பைடு நூலகம்
P13
P14
P23
P12
P24
P34
（f ）
2（B）、在如图所示的机构中，已知Φ1 =45° ω1=100rad/s,方向为逆时针 方向，求构件1与构件3在该位置的速度瞬心P13以及构件3的速度v3.