材料力学计算题
材料力学试题及答案解析7套

材料力学试卷1一、结构构件应该具有足够的 、 和 。
(本题3分) 二、低碳钢拉伸破坏经历了四个典型阶段: 阶段、 阶段、 阶段和 阶段。
衡量材料强度的指标是 、 。
(本题6分) 三、在其他条件不变的前提下,压杆的柔度越大,则临界应力越 、临界力越 ;材料的临界柔度只与 有关。
(本题3分) 四、两圆截面杆直径关系为:123D D =,则12Z Z I I =;12Z Z W W =;12P P I I =;12P P W W =; (本题8分)五、已知构件上危险点的应力状态,计算第一强度理论相当应力;第二强度理论相当应力;第三强度理论相当应力;第四强度理论相当应力。
泊松比3.0=μ。
(本题15分)六、等截面直杆受力如图,已知杆的横截面积为A=400mm 2, P =20kN 。
试作直杆的轴力图;计算杆内的最大正应力;材料的弹性模量E =200Gpa ,计算杆的轴向总变形。
(本题15分)七、矩形截面梁,截面高宽比h=2b,l=4米,均布载荷q=30kN/m许用应力[]MPa100=σ,1、画梁的剪力图、弯矩图2、设计梁的截面(本题20分)。
八、一圆木柱高l=6米,直径D=200mm ,两端铰支,承受轴向载荷F=50kN,校核柱子的稳定性。
已知木材的许用应力[]MPa10=σ,折减系数与柔度的关系为:23000λϕ=。
(本题15分)九、用能量法计算结构B 点的转角和竖向位移,EI 已知。
(本题15分)材料力学试卷2一、(5分)图(a )与图(b )所示两个矩形微体,虚线表示其变形后的情况,确定该二微体在A 处切应变b aγγ的大小。
二、(10分)计算图形的惯性矩yz I I 。
图中尺寸单位:毫米。
三、(15分)已知构件上危险点的应力状态,计算第三强度理论相当应力;第四强度理论相当应力。
四、(10分)画图示杆的轴力图;计算横截面上最大正应力;计算杆最大轴向应变ε。
已知杆的横截面积A =400 mm 2,E =200GPa 。
四套《材料力学》试题及答案

材料力学试题A成绩班 级 姓名 学号 一、单选题(每小题2分,共10小题,20分)1、 工程构件要正常安全的工作,必须满足一定的条件。
下列除( )项,其他各项是必须满足的条件。
A 、强度条件B 、刚度条件C 、稳定性条件D 、硬度条件 2、内力和应力的关系是( )A 、内力大于应力B 、内力等于应力的代数和C 、内力是矢量,应力是标量D 、应力是分布内力的集度 3、根据圆轴扭转时的平面假设,可以认为圆轴扭转时横截面( )。
A 、形状尺寸不变,直径线仍为直线。
B 、形状尺寸改变,直径线仍为直线。
C 、形状尺寸不变,直径线不保持直线。
D 、形状尺寸改变,直径线不保持直线。
4、建立平面弯曲正应力公式zI My =σ,需要考虑的关系有( )。
A 、平衡关系,物理关系,变形几何关系;B 、变形几何关系,物理关系,静力关系;C 、变形几何关系,平衡关系,静力关系;D 、平衡关系, 物理关系,静力关系; 5、利用积分法求梁的变形,不需要用到下面那类条件( )来确定积分常数。
A 、平衡条件。
B 、边界条件。
C 、连续性条件。
D 、光滑性条件。
6、图示交变应力的循环特征r 、平均应力m σ、应力幅度a σ分别为( )。
A -10、20、10;B 30、10、20; C31-、20、10; D 31-、10、20 。
7、一点的应力状态如下图所示,则其主应力1σ、2σ、3σ分别为( )。
A 30MPa 、100 MPa 、50 MPaB 50 MPa 、30MPa 、-50MPaC 50 MPa 、0、-50Mpa 、D -50 MPa 、30MPa 、50MPa8、对于突加载的情形,系统的动荷系数为( )。
A 、2 B 、3 C 、4 D 、5 9、压杆临界力的大小,( )。
A 与压杆所承受的轴向压力大小有关;B 与压杆的柔度大小有关;C 与压杆材料无关;D 与压杆的柔度大小无关。
10、利用图乘法计算弹性梁或者刚架的位移,要求结构满足三个条件。
(完整版)材料力学试题及答案
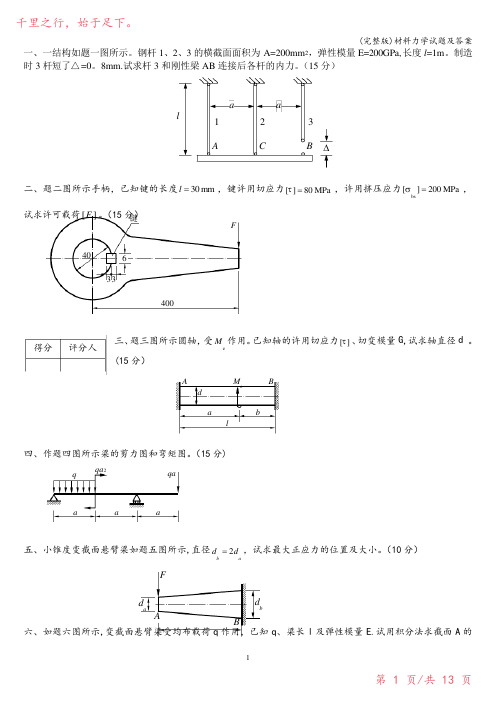
一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2,弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
(15分)aalABC123∆二、题二图所示手柄,已知键的长度30 mm l =,键许用切应力[]80 MPa τ=,许用挤压应力bs[]200 MPa σ=,试求许可载荷][F 。
(15分)三、题三图所示圆轴,受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分)四、作题四图所示梁的剪力图和弯矩图。
(15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =,试求最大正应力的位置及大小。
(10分)六、如题六图所示,变截面悬臂梁受均布载荷q 作用,已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .(15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
(15分)一、(15分)(1)静力分析(如图(a))1N F2N F3N F图(a)∑=+=231,0N N N yF F F F(a)∑==31,0N N CF F M(b)(2)几何分析(如图(b))1l∆2l∆3l∆∆图(b)wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3)物理条件EA l F l N 11=∆,EA l F l N 22=∆,EAl F l N 33=∆ (4)补充方程∆=++EAlF EA l F EA l F N N N 3212 (c) (5)联立(a)、(b)、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分)以手柄和半个键为隔离体,S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体,bsS20F F F ==由剪切:S []s FA ττ=≤,720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、(15分)eABM M M +=0ABϕ=, A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+;当b a >时 e316π ()[]M bd a b τ≥+。
材料力学第二章计算题

1.杆系结构如图所示,已知杆AB、AC材料相同,丨-160 MPa,横截面积分别为A i = 706.9 mm2,A2=314 mm2,试确定此结构许可载荷[P]。
(15分)2.在图示直径为d=10mm的等直圆杆,沿杆件轴线作用F1、F2、F3、F4。
已知:F仁6kN, F2=18kN, F3=8kN, F4=4kN,弹性模量E=210GPa试求各段横截面上的轴力及作轴力图并求杆的最大 ________ 拉应力及压应力。
3•图示吊环,载荷F=1000KN两边的斜杆均由两个横截面为矩形的钢杆构成,杆的厚度和宽度分别为b=25mm h=90mm斜杆的轴线与吊环对称,轴线间的夹角为 a =20°。
钢的许用应力[6 ]=120Mpa。
试校核斜杆的强度。
4.钢质圆杆的直径d=10mm,F=5kN,弹性模量E=210GPa试作轴力图并求杆的最大正应力。
5.图示板状硬铝试件,中部横截面尺寸a= 2mm , b = 20mm。
试件受轴向拉力P = 6kN作用,在基长I = 70mm 上测得伸长量 =1 = 0.15mm ,板的横向缩短 =b = 0.014mm 。
试求板材 料的弹性模量E 及泊松比。
6 •钢制直杆,各段长度及载荷情况如图。
各段横截面面积分别为=200mm 2。
材料弹性模量 E = 200GPa 。
材料许用应力[tr ]=210MPa 。
试作杆的轴力图并校核杆的强度。
2 7.图示钢杆的横截面面积为 A =200mm ,钢的弹性模量E =200GP a ,求各端杆的应变、 伸长及全杆的总伸长 。
&等截面实心圆截面杆件的直径 d=40mm ,材料的弹性模量 E=200GPa 。
AB = BC = CD = 1m ,在B 、C 、D 截面分别作用有 P 、2P 、2P 大小的力,方向和作用线如图所示, P=10KN 。
①做此杆件的轴力图;②求此杆件内的最大正应力;③求杆件 C 截面的铅垂位移。
材料力学期末考试复习题及答案
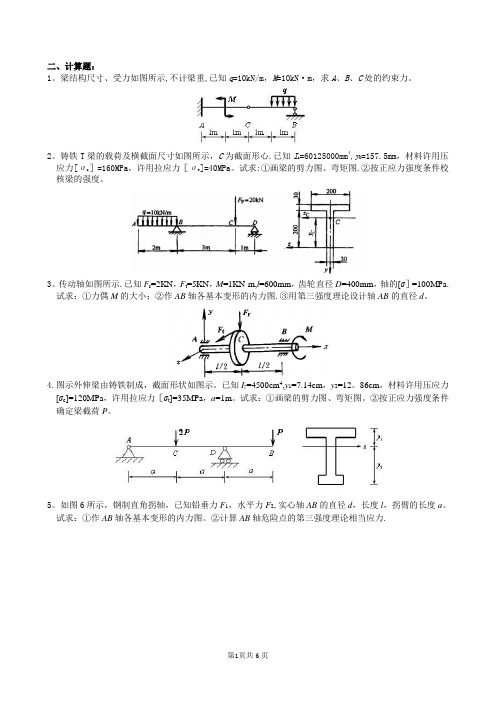
二、计算题:1。
梁结构尺寸、受力如图所示,不计梁重,已知q=10kN/m,M=10kN·m,求A、B、C处的约束力。
2。
铸铁T梁的载荷及横截面尺寸如图所示,C为截面形心.已知I z=60125000mm4,y C=157.5mm,材料许用压应力[σc]=160MPa,许用拉应力[σt]=40MPa。
试求:①画梁的剪力图、弯矩图.②按正应力强度条件校核梁的强度。
3。
传动轴如图所示.已知F r=2KN,F t=5KN,M=1KN·m,l=600mm,齿轮直径D=400mm,轴的[σ]=100MPa.试求:①力偶M的大小;②作AB轴各基本变形的内力图.③用第三强度理论设计轴AB的直径d。
4.图示外伸梁由铸铁制成,截面形状如图示。
已知I z=4500cm4,y1=7.14cm,y2=12。
86cm,材料许用压应力[σc]=120MPa,许用拉应力[σt]=35MPa,a=1m。
试求:①画梁的剪力图、弯矩图。
②按正应力强度条件确定梁截荷P。
5。
如图6所示,钢制直角拐轴,已知铅垂力F1,水平力F2,实心轴AB的直径d,长度l,拐臂的长度a。
试求:①作AB轴各基本变形的内力图。
②计算AB轴危险点的第三强度理论相当应力.6.图所示结构,载荷P=50KkN,AB杆的直径d=40mm,长度l=1000mm,两端铰支。
已知材料E=200GPa,σp=200MPa,σs=235MPa,a=304MPa,b=1。
12MPa,稳定安全系数n st=2.0,[σ]=140MPa.试校核AB杆是否安全。
7.铸铁梁如图5,单位为mm,已知I z=10180cm4,材料许用压应力[σc]=160MPa,许用拉应力[σt]=40MPa,试求:①画梁的剪力图、弯矩图.②按正应力强度条件确定梁截荷P。
8.图所示直径d=100mm的圆轴受轴向力F=700kN与力偶M=6kN·m的作用。
已知M=200GPa,μ=0.3,[σ]=140MPa。
材料力学试卷试题(附参考答案)

一、简单计算题(共38分)1.如图所示是一枚被称为“孔方兄”的中国古钱币,设圆的直径为d ,挖去的正方形边长为b ,若2/d b =,求该截面的弯曲截面系数Z W 。
(6分)2. 已知某点处的应力状态如图所示,,MPa 100,MPa 60==στ弹性模量GPa 200=E ,泊松比25.0=ν,求该点处的三个主应力及最大正应变。
(6分)3.试画出低碳钢的拉伸应力-应变曲线,并在图上标出4个极限应力。
(4分)y4.已知交变应力的,MPa 5,MPa 3min max -==σσ, 求其应力循环特征r 及应力幅度a σ。
(4分)5.如图所示为矩形截面悬臂梁,在梁的自由端突然加一个重为Q 的物块,求梁的最大弯曲动应力。
(4分)Qhb6.如图所示为两根材料相同的简支梁,求两梁中点的挠度之比b a w w /。
(4分)7.两块相同的钢板用5个铆钉连接如图所示,已知铆钉直径d ,钢板厚度t ,宽度b ,求铆钉所受的最大切应力,并画出上钢板的轴力图。
(6分))(b2/L 2/L )(a P8.超静定结构如图所示,所有杆件不计自重,AB为刚性杆,试写出变形协调方程。
(4分)Pa a a 2/AF二、作图示梁的剪力图与弯矩图。
(10分)三、不计剪力的影响,已知EI ,试用能量法求图示悬臂梁自由端的挠度A w 。
(12分)四、铸铁梁的载荷及截面尺寸如图所示,其中4cm 5.6012,mm 5.157==Z C I y 。
2A C已知许用拉应力MPa 40][=t σ,许用压应力MPa 160][=C σ。
试按正应力条件校核梁的强度。
若载荷不变,但将截面倒置,问是否合理?为什么? (14分)五、圆截面直角弯杆ABC 放置于图示的水平位置,已知cm 50=L ,水平力(单位:mm )200kN 40=F ,铅垂均布载荷m /kN 28=q ,材料的许用应力MPa 160][=σ,试用第三强度理论设计杆的直径d 。
材料力学例题
G=80GPa ,许用剪应力 []=30MPa,试设计杆
的外径;若[]=2º /m ,试校核此杆的刚度,并
求右端面转角。
[例题] 某传动轴设计要求转速n = 500 r / min,输入功率P1 = 500 马力, 输出功率分别 P2 = 200马力及 P3 = 300马力,已 知:G=80GPa ,[ ]=70M Pa,[ ]=1º /m ,试确定: ①AB 段直径 d1和 BC 段直径 d2 ? ②若全轴选同一直径,应为多少? ③主动轮与从动轮如何安排,轴的受力合理? P2 A 500 B 400 P3 C
例题 油缸活塞直经 D = 65mm,油压 p =1.2MPa.活塞杆长度 l=1250mm,材料为35钢,s =220MPa,E = 210GPa,[nst] = 6.试确定活塞杆的直经.
活塞杆 D p d 活塞
例题
AB的直径 d=40mm,长 l=800mm,两端可视为铰支. 材
料为Q235钢,弹性模量 E = 200GPa. 比例极限p =200MPa,屈
传动轴的直径为d=40毫米,皮带轮的直径分别为:右侧轮直 径D1=200毫米,右侧轮D2=120毫米,皮带的张力为F1=2F2 =4KN,F3=2F4。轴的许用应力为:[σ]=100MPa,用第三 强度理论校核轴的强度。
例题
外径 D = 50 mm,内径 d = 40 mm 的钢管,两端铰支,
材料为 Q235钢,承受轴向压力 F. 试求 (1)能用欧拉公式时压杆的最小长度;
例题
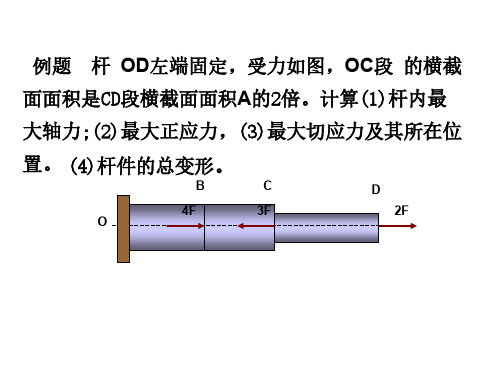
杆 OD左端固定,受力如图,OC段 的横截
面面积是CD段横截面面积A的2倍。计算(1)杆内最
大轴力;(2)最大正应力,(3)最大切应力及其所在位 置。 (4)杆件的总变形。
材料力学试题及答案

材料力学试题及答案一、选择题1. 材料力学中,下列哪个参数是用来描述材料在受力时抵抗变形的能力?A. 弹性模量B. 屈服强度C. 抗拉强度D. 断裂韧性答案:A2. 以下哪种材料在受力后能够完全恢复原状?A. 弹性体B. 塑性体C. 粘弹性体D. 脆性体答案:A3. 应力集中现象主要发生在哪种情况下?A. 材料表面存在缺陷B. 材料内部存在孔洞C. 材料受到均匀分布的载荷D. 材料受到单一集中载荷答案:D4. 根据胡克定律,当应力不超过比例极限时,应力与应变之间的关系是:A. 线性的B. 非线性的C. 指数的D. 对数的答案:A5. 材料的疲劳破坏是指在何种条件下发生的?A. 单次超负荷B. 长期重复载荷C. 瞬间高温D. 腐蚀环境答案:B二、填空题1. 在简单的拉伸和压缩实验中,应力(σ)是力(F)与横截面积(A)的比值,即σ=______。
答案:F/A2. 材料的韧性是指其在断裂前能够吸收的能量,通常通过______试验来测定。
答案:冲击3. 当材料在受力时发生塑性变形,且变形量随时间增加而增加,这种现象称为______。
答案:蠕变4. 剪切应力τ是剪切力(V)与剪切面积(A)的比值,即τ=______。
答案:V/A5. 材料的泊松比是指在单轴拉伸时,横向应变与纵向应变的比值,通常用希腊字母______表示。
答案:ν三、简答题1. 请简述材料弹性模量的定义及其物理意义。
答:弹性模量,又称杨氏模量,是指材料在弹性范围内抵抗形变的能力的量度。
它定义为应力与相应应变的比值。
物理意义上,弹性模量越大,表示材料在受力时越不易发生形变,即材料越硬。
2. 描述材料的屈服现象,并解释屈服强度的重要性。
答:屈服现象是指材料在受到外力作用时,由弹性状态过渡到塑性状态的过程。
在这个过程中,材料首先经历弹性变形,当应力达到某个特定值时,即使应力不再增加,材料也会继续发生显著的塑性变形。
屈服强度是衡量材料开始屈服的应力值,它对于工程设计和材料选择具有重要意义,因为它决定了结构在载荷作用下的安全性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算题
一等截面杆在轴向拉力P作用下,测得杆件A点处的横向线应变0.00003,已知杆的横
截面积A 300mm2,材料的弹性模量E 2 105
MPa、泊松比0.28,试求(1)轴向拉力的数值;(2)图1所示A点在图2截面处的正应力和剪应力。
解:(1)
E E —=21.42857 MPa
P F N A E A E — A=6.43X 103N
x
- cos60.
2 2
16.07MPa
— sin 60
2
9.28MPa
(2)在A点取单元体,并画A点的应力状态图
xy
21.43MPa
cos2
xy
sin 2
-sin 2
xy
cos2
12
计算题
杆件上同时作用有如图所示的轴向力和横向力, 大小均为P 10kN ,杆件的截面为方形截面,
截面边长为a=100mm ,杆件长度为l=1m 。
试求出杆件的最大、最小正应力的大小。
带入可得弯曲max •怜2 6里
a 2 a 12
则最大、最小正应力为:
P M max 3
弯曲max ―
2 4
a a 2解答:
画出其轴力图和弯矩图。
杆件的轴向应力为 杆件的最大弯矩为 P 轴 P/A 右(拉应力)
a
M max Pl
max
弯曲max y max
max min
计算题
承受均布荷载作用的矩形截面木梁如图所示,已知l=4m
,
b=140mm , h=210mm , q=2kN/m , 弯曲时木材的容许正应力[]10MPa,(1)校核该梁的强度;(2)计算该梁能承受的极限
q
11 M H 11 { M I
l
解答:
ql
(1)做梁的弯矩图,梁的最大正应力发生在跨中弯矩最大的截面上,最大弯矩为:
1 2 1 3 2 3
叽x 8ql 8 2 10 4 4 10 Nm
抗弯截面模量为:
1 2 1 22 3
w z -bh2- 0.14 0.212 0.103 10 2m3
6 6
最大正应力为
满足强度条件。
(2)根据梁的强度条件,梁的容许承受的最大弯矩为:
M max W z[]
1
将M max ?q|2带入,即1 2
ql W Z[]
8
从而梁的容许承受的极限荷载为:
8W z[] 2 6
8 0.103 10 10 10
l242
5.15kN /m
max
4 103
max
W z 2
0.103 10
3.88MPa
计算题: 图中为一松木压杆(P 59 )的示意图,其两端的支承情况为:下端固定,上端在 面内不能水平移动与转动,在 h 150mm , 定角度出发, 材料的弹性模量 确
定最合理的 xoz 平面内可水平移动与转动。
已知 I 3m ,b E 10 103MPa 。
( 1 )计算该压杆的临界力;(2) xoy 平 100mm , 从该杆的稳
b 与h 的比值。
= 0.5 xoy 平面 T h t
r
h + z xoz 平 面 解:(1)计算临界力 由于杆的上端在xoy (纸面平面) 而,压杆在这两个平面内的柔度 面内的柔度值分别为 xoz (与纸面平面垂直的平面)内的支撑情况不同,因 不同,压杆将在 值大的平面内失稳。
压杆在 xoy 和xoz xoy 面 z 1l i l b -12 °5 L 52 0.1 ‘1; xoz 平面 2l y
I y 2I '1 h :— 0.15 A ■ 12 2 3
=138.6 1 12 该杆若失稳,将发生在 xoz 面内,y p 59,故可用欧拉公式计算临界力,其 值为
2 3 6 10 10 10 'El y (2l )2 确定合理的b 与h 的比值 (2 3)2
3
0.1 0.12 12 77.1kN (2) 合理的b 与h 的比值,应该使在 xoy 和xoz 两个平面内具有相同的稳定性,即应使两个平面 的临界力 2 —相等。
依据P cr F Cr 有 (2l ) 2匚 hb 3
12 2 (1l)
bh 3 2E 12
2 (2l)
得b/ h 1/ 4 ,即为从稳定考虑该杆横截面尺寸最合理的比值。
