圆台等展开面积计算及自动出图
天圆地方计算方法
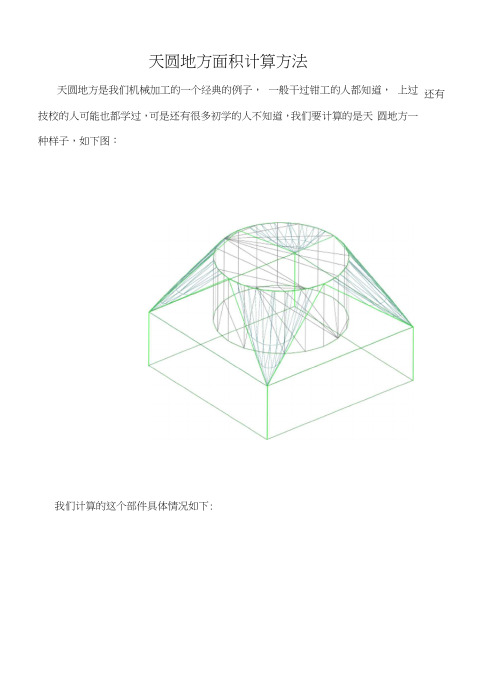
天圆地方面积计算方法天圆地方是我们机械加工的一个经典的例子，一般干过钳工的人都知道，上过技校的人可能也都学过，可是还有很多初学的人不知道，我们要计算的是天圆地方一种样子，如下图：我们计算的这个部件具体情况如下:还有1. 地方的方是S=4380mm,方的高度是H=28 mm。
2. 地方上表面到天圆顶面的垂直距离是H仁1170 mm。
3. 天圆的圆的直径是D=3170 mm。
求的是在天圆顶面和地方上表面连接处的面积，这个面积分成了八块，两种形状，一种是圆台的外圈的四分之一，是由两条直线和天圆顶圆的周长的四分之一圆弧组成，是带弧状的倒三角。
第二种是由地方上表面的边线和地方边线和边线的交点和天圆顶面圆四分之一处象限点的连线组成一个等腰三角形，我们要计算的就是这两种形状的面积，周长，展开图，和展开图的各个要素的具体情况。
第一种，如下:2 3 32 . 3此图是第一种形状，带弧状的倒三角展开后的形状，为什么是这样的形状呢,是因为带弧状的倒三角是圆台的四分之一面积，下面是圆台展开图：我们要计算的是圆台的母线长和大圆锥的母线长，（我们说的大圆锥是地方对角线为底圆直径的圆锥）我们设大圆锥的母线长为R1，圆台的母线长为r1,圆台上圆锥的母线为r，圆台高度为H仁1170mm，大圆锥底面直径为R仁4380X ... 2 =6194求圆台的母线和大圆锥的母线：r1=1912r2 3170/2R1 一6194/2R1=(r2+r1)= (r2+1912)r2 _1585r2 1912 一3097r2=2004 R仁3916弧形三角形的圆弧周长为天圆周长的四分之一，L1=1/4LL= nx D=3.14X 3170〜9952L1 = 1/4L=9952 - 4=2488小圆锥周长为L2L=2xnx r2=2 x3・14X 2004〜12585圆弧三角形的展开面积在小圆锥的展开面积中占的的比例为Q只要知道圆弧三角形的圆弧在小圆锥的周长中占多少，因为圆一周是360度，先求得占多少比例就能知道圆弧三角形的圆弧在小圆锥中的圆心角A是多少，Q=2488/12585 〜0.198A=0.198 X 360°=71.2H2= 2r2sin =23322AH4=2r2COS2=1629^（H4是圆心到圆弧弦长的距离）22 H2 2（R1H4）（）和3r3=2556H 2圆心角C= 2arcsin =54°2r3这样就能得到天圆地方的第一种形状的计算方法，并且和他的展开图，而且可以开始能下料了，把第一种形状的展开的内凹扇形卷成原来的带弧形的三角和第二种形状拼起来，就可得到我们所需要的把天圆地方连接起来的中间形状•也可把天圆地方画在实体制图软件中进行实体建模，得到r3=2556长，同时也能得出第二种形状22 S 2(H3) (J 訂3 2 H3=13仃 圆心角 B= arcsin^3 =54r3。
高中数学圆台面积公式
高中数学圆台面积公式
圆台是由一个圆和一个平行于底面的截面生成的几何体，它的底面是
一个圆，侧面是根据底面的半径和高度生成的曲面。
计算圆台的面积需要
知道底面的半径和圆台的高度。
圆台的底面是一个圆，其面积计算公式为：
S₁=πr₁²
由于底面积是圆的面积，因此这个公式可以看作是圆的面积公式，我
们可以称之为圆台的底面积公式。
圆台的侧面是由底圆的半径和圆台的高度生成的曲面。
为了计算圆台
的侧面积，我们需要计算出侧面的长度。
首先我们可以通过勾股定理计算出圆台的斜高，斜高的计算公式如下：s=√(h²+(r₁-r₂)²)
其中，s为圆台的斜高，h为圆台的高度，r₁为底面的半径，r₂为顶面的半径，当r₁和r₂相等时，斜高与高度即可相等。
根据斜高，可以计算出圆台的侧面积公式为：
S₂=π(r₁+r₂)s
其中，S₂为圆台的侧面积。
最后，圆台的总表面积等于底面积和侧面积之和，并且可以用以下公
式表示：
S=S₁+S₂
其中，S为圆台的总表面积。
下面我们将用一个例子来演示如何根据给定的半径和高度计算圆台的面积。
例：半径为3 cm，高度为5 cm的圆台的面积计算。
首先计算底面积
然后计算侧面积，首先计算斜高：
s = √(5² + (3 - 3)²) = √(25 + 0) = 5 cm
再根据侧面积公式：
最后计算总表面积：
S = S₁ + S₂ = 28.27 + 94.25 ≈ 122.52 cm²
所以，半径为3 cm，高度为5 cm的圆台的面积为122.52 cm²。
圆台的表面积公式
圆台的表面积公式
表面积公式：S=πr+πR+πRl+πrl=π(r+R+Rl+rl)。
r－上底半径、R－下底半径、h－高、l—母线=根号下[（R-r）+h]
体积公式
九章算术记载的圆台体积公式：“上下周相乘，又各自乘，并之，以高乘之，三十六而一、”这是将圆周率的值取为3得到的。
其中r'是上底面半径，r是下底面半径。
实际上圆面积与方形面积形成有相同之处。
方形面积形成，是一根直线，向一个方向，横向同时均速移动两端，所形成了正方形或长方形。
圆面积的形成是，一根直线，固定一端，移动另一端，绕一周形成了圆形。
所以圆面积也可以这样去算，周长乘半经除貮。
圆台表面积的推导过程
圆台表面积的推导过程
一、引言
圆台是一种三维几何体，由两个同心圆底面和一个侧面围成。
在日常生活中，圆台广泛用于各种实际问题中，如圆柱形储罐、管道等。
因此，掌握圆台表面积的计算方法对于解决实际问题具有重要意义。
本篇文档将详细介绍圆台表面积的推导过程，以便读者更好地理解和应用。
二、圆台侧面积计算
圆台的侧面积计算是推导其表面积的关键步骤。
首先，我们需要了解圆台的侧面积公式。
圆台的侧面积公式为：侧面积=π*(R+r)*l，其中R和r分别为圆台的上底面和下底面半径，l为圆台的高。
三、圆台上下底面积计算
接下来，我们需要计算圆台的上底面和下底面面积。
上底面半径为R，下底面半径为r，因此上底面面积为π*R^2，下底面面积为π* r^2。
四、圆台表面积公式推导
根据上述计算结果，我们可以得出圆台的表面积公式为：表面积=侧面积+上底面面积+下底面面积。
将侧面积、上底面面积和下底面面积的公式代入，得到：表面积=π*(R+r)*l+π*R^2+π*r^2。
五、结论
通过以上推导过程，我们可以得出圆台的表面积公式为：表面积=π*(R+r)*l+π*R^2+π*r^2。
这个公式可以用于计算给定参数的圆
台的表面积，为解决实际问题提供了重要工具。
在应用该公式时，请注意保证输入参数的正确性，以获得准确的结果。
圆台展开计算范文
圆台展开计算范文
首先，我们来看一下圆台的基本几何特征。
一个圆台由两个平行且相似的圆组成，底面圆称为大圆，顶面圆称为小圆。
圆台的高度是垂直于大圆和小圆底面的直线段，沿着这条直线段可以连接大圆和小圆的点。
圆台的侧面是由连接大圆和小圆相对应的点的曲面组成。
要展开圆台，我们可以按照以下步骤进行：
1.首先，将圆台的侧面沿着高度剖开。
这样我们就得到一个扇形，其中的一条边是大圆的弧，另一条边是小圆的弧，扇形的中心角度等于两个底面圆的圆心角度的差值。
2.接下来，将扇形展开为一个矩形。
将扇形的一条边作为矩形的一条边，并按照扇形的中心角度将矩形剖开。
将扇形的弧长度等分，然后在矩形的另一条边上取相应的点。
3.将矩形按照扇形的弧长度比例进行展开。
将扇形的每一小部分对应的点依次连接，形成展开图形。
4.最后，我们可以计算出展开图形的总面积和周长。
展开图形的总面积等于矩形的面积，周长等于小圆的弧长。
根据展开图形的特点，我们可以计算圆台的表面积和体积。
圆台的表面积可以通过展开图形的总面积减去两个底面圆的面积得到。
而圆台的体积可以通过底面圆的面积乘以高度再除以3得到。
总之，圆台展开计算是一种将圆台展开为平面图形的方法，通过展开图形的特点可以计算出圆台的表面积和体积。
通过了解圆台的基本几何特征以及展开的步骤，我们可以进行圆台展开计算并得到准确的结果。
推导圆台的表面积公式
推导圆台的表面积公式圆台是指由一个底圆和与底圆平行的侧面组成的几何体。
在几何学中，我们可以通过推导来得到圆台的表面积公式。
下面，我将按照推导的逻辑顺序，依次介绍推导圆台表面积公式的过程。
首先，我们需要明确圆台的几何特征。
一个圆台由一个底圆和与底圆平行的侧面组成，底圆的半径为r，侧面的高度为h，侧面与底圆的夹角为α。
我们的目标是推导出圆台的表面积公式。
我们从最简单的情况开始推导。
考虑一个底圆半径为r，侧面高度为h，且侧面与底圆夹角为90度的情况。
这样的圆台可以看作是一个圆柱体，它的表面积公式为：圆台的侧面积= 2πrh圆台的底面积= πr^2圆台的表面积 = 底面积 + 侧面积= πr^2 + 2πrh接下来，我们考虑圆台侧面与底圆非垂直的情况。
我们将侧面与底面的交线固定在底面上的一个点P上，构造直角三角形OPQ（如下图所示），其中O为底面圆心，Q为圆台侧面与底面的交线与圆心O的连线与底面的交点，P为底面上的固定点。
[图]O/ |/ |/ |/ |/ |P Q|_____|在直角三角形OPQ中，OQ为圆台的半径r，OP为圆台的高度h，PQ为圆台的侧面与底面的交线段长度。
根据勾股定理，我们可以得到：OQ^2 = OP^2 + PQ^2将OQ替换为r，OP替换为h，我们可以得到：r^2 = h^2 + PQ^2化简后可得：PQ = √(r^2 - h^2)由几何性质可知，当交线固定时，所有的Q点构成底面上的圆，其半径等于圆台的半径r。
因此，PQ实际就是底面圆的周长，即2πr。
我们可以得到以下关系式：PQ = 2πr将上述关系式代入之前的公式，我们可以得到圆台的侧面积公式：圆台的侧面积= PQ×h = 2πrh综上所述，当圆台的底圆半径为r，侧面高度为h，侧面与底圆夹角为α时，圆台的表面积公式为：圆台表面积 = 底面积 + 侧面积= πr^2 + 2πrh通过以上的推导过程，我们得到了圆台的表面积公式。
圆台公式面积
圆台公式面积圆台是由一个圆和与其共面但不同心的一个圆锥截面组成的几何体，圆台的面积是指圆台的所有表面积之和。
下面我们来详细介绍一下圆台的面积计算公式。
圆台的表面积由两部分组成：底面积和侧面积。
首先，我们先计算底面积。
底面积是指圆台的底部圆的面积。
根据圆的面积公式，圆的面积等于圆的半径的平方乘以π（即πr²）。
假设圆台的底部圆的半径为r₁，那么底面积可以表示为πr₁²。
接下来，我们计算侧面积。
侧面积是指圆台侧面的面积，可以看作是一个弧形的扇形面积再加上一段直线的矩形面积。
我们用弧长公式计算弧形的扇形面积。
弧形的扇形面积等于圆台的斜高（即圆台的母线）乘以底面圆的弧长的一部分。
圆台的斜高可以通过勾股定理求得，即斜高的平方等于圆台的高的平方加上底面圆半径的差的平方（h² = (H - h)² + (r₂- r₁)²）。
假设圆台的高为H，底面圆的半径为r₁，顶面圆的半径为r₂，斜高为h，底面圆的弧长为L₁，顶面圆的弧长为L₂，那么弧形的扇形面积可以表示为L₁ * h / L₂。
而矩形面积等于矩形的长乘以宽，其中矩形的长等于底面圆的弧长的一部分（L₁），矩形的宽等于圆台的斜高（h）。
所以矩形面积可以表示为L₁ * h。
因此，侧面积等于弧形的扇形面积加上矩形面积，即L₁* h / L₂+ L₁ * h。
将底面积和侧面积相加，即可得到圆台的总面积。
圆台的面积计算公式可以表示为：底面积 + 侧面积= πr₁² + L₁ * h / L₂ + L₁ * h。
需要注意的是，在计算圆台的面积时，需要确保所使用的单位一致。
如果底面圆的半径和高的单位不同，那么在计算时需要进行单位换算。
圆台的面积计算公式是一个较为复杂的公式，涉及到圆的面积、勾股定理以及弧长公式等知识。
通过正确使用这个公式，我们可以准确计算圆台的面积，为解决实际问题提供了便利。
圆台计算公式
圆台计算公式圆台，这可是个在数学世界里挺有趣的家伙！咱先来说说圆台的计算公式到底是啥。
圆台的体积公式是：V = 1/3 × π × h × (R² + r² + R × r) ，其中 V 表示体积，h 是圆台的高，R 是上底面半径，r 是下底面半径。
面积公式呢，包括侧面积和表面积。
侧面积S = π × l × (R + r) ，l 是母线长。
表面积S = π × (r² + R² + l × r + l × R) 。
那这公式咋用呢？给您举个例子。
比如说，有个圆台形状的花坛，上底面半径是 2 米，下底面半径是 3 米，高是 1.5 米。
咱来算算它的体积。
先算出上底面积是π×2² = 4π 平方米，下底面积是π×3² = 9π 平方米。
然后把数值代入体积公式，V = 1/3 × π × 1.5 × (4 + 9 + 2×3) ，经过计算就能得出这个花坛的体积啦。
我还记得有一次，我带着学生们在校园里实地测量一个圆台形状的小雕塑。
同学们那股认真劲儿，真是让人印象深刻。
有的同学拿着尺子量上底面半径，有的量下底面半径，还有的负责记录数据。
大家七嘴八舌地讨论着，“哎呀，这个尺子不太够长呢！”“咱们得量准点，不然算出来就错啦！”大家忙得不亦乐乎。
回到教室后，我们一起根据测量的数据来计算这个圆台雕塑的体积和表面积。
在计算的过程中，有的同学粗心算错了，旁边的小伙伴赶紧指出来，“你这里算错啦，再好好想想！”大家互相帮助，最终都算出了正确的结果。
通过这次实践，同学们对圆台的计算公式理解得更透彻了，也明白了数学在生活中的实际应用。
其实啊，圆台的计算公式不仅仅是一堆数字和符号的组合，它更是我们解决实际问题的有力工具。