对数平均与高考压轴题
对数平均数
高考又见对数平均数在历年的高考压轴题中我们总是能见到对数平均数的影子。
2018年高考理科数学全国Ⅰ卷的压轴题最后一问,实际上就是对数平均数不等式的应用。
加强对对数平均数的理解,无疑能对我们解决压轴题有很大的帮助。
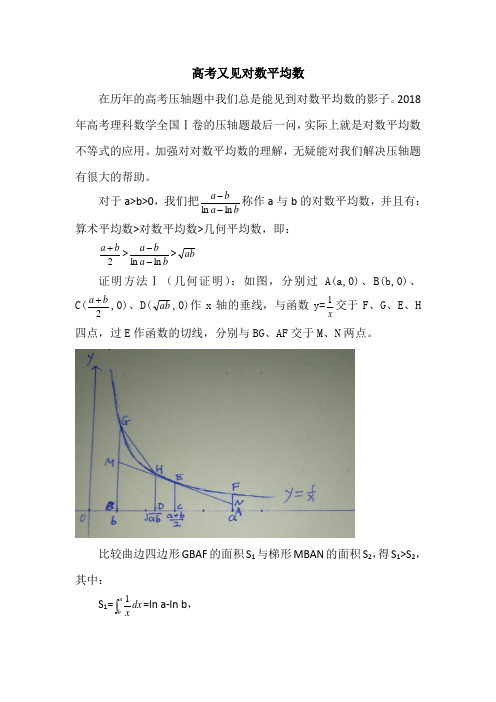
对于a>b>0,我们把ba ba ln ln --称作a 与b 的对数平均数,并且有:算术平均数>对数平均数>几何平均数,即:2b a +>ba ba ln ln -->ab 证明方法Ⅰ(几何证明):如图,分别过A(a,0)、B(b,0)、C(2b a +,0)、D(ab ,0)作x 轴的垂线,与函数y=x1交于F 、G 、E 、H 四点,过E 作函数的切线,分别与BG 、AF 交于M 、N 两点。
比较曲边四边形GBAF 的面积S 1与梯形MBAN 的面积S 2,得S 1>S 2,其中:S 1=⎰ab dx x1=ln a-ln b ,S 2=2AN BM +•AB=CE •AB=ba +2•(a-b) ∴ ln a-ln b>ba +2•(a-b)即:2b a +>ba b a ln ln --……①比较梯形GBDH 的面积S 3与曲边四边形GBDH 的面积S 4,得S 3>S 4,其中:S 3=21(GB+HD)•BD=21(b 1+ab 1)(ab -b)=abb a 2- S 4=⎰abb dx x 1=ln ab -ln b=2ln ln b a +-ln b=2ln ln ba - ∴abb a 2->2ln ln b a -即:ba ba ln ln -->ab ……②综合①②,得:2b a +>ba ba ln ln -->ab (a>b>0)证明方法Ⅱ(函数证明): 令f(x)=2ln x +12+x -1 (x>1),则有: f`(x)=x 21-2)1(1+x =22)1(24)1(+-+x x x x =22)1(2)1(+-x x x >0 ∴ f(x)>f(1)=0,即:2ln x +12+x -1>0, 令x=b a ,代入整理得: 2ln ln b a ->b a b a +-即:2b a +>ba b a ln ln --……①令g(x)=x-2•ln x-x1(x>1),则有:g`(x)=1-x 2+21x=22)1(x x ->0∴ g(x)>g(1)=0,即x-2•ln x-x1>0, 令x=b a ,代入整理得:abba ->ln a-ln b即:ba ba ln ln -->ab ……②综合①②,得:2b a +>ba ba ln ln -->ab (a>b>0)经过上述证明,我们对对数平均数有了一定的了解,接下来看一看2018年高考数学理科全国Ⅰ卷第21题:已知函数f(x)=x1-x+a •ln x (1) 讨论f(x)的单调性;(2) 若f(x)存在两个极值点x 1、x 2,求证:2121)()(x x x f x f --<a-2第一问略。
2025高考数学必刷题 第10讲、对数与对数函数(教师版)

第10讲对数与对数函数知识梳理1、对数式的运算(1)对数的定义:一般地,如果(0x a N a =>且1)a ≠,那么数x 叫做以a 为底N 的对数,记作log a x N =,读作以a 为底N 的对数,其中a 叫做对数的底数,N 叫做真数.(2)常见对数:①一般对数:以(0a a >且1)a ≠为底,记为log Na ,读作以a 为底N 的对数;②常用对数:以10为底,记为lg N ;③自然对数:以e 为底,记为ln N ;(3)对数的性质和运算法则:①1log 0a =;log 1aa =;其中0a >且1a ≠;②log Na a N =(其中0a >且1a ≠,0N >);③对数换底公式:log log log c a c bb a=;④log ()log log a a a MN M N =+;⑤log log log aa a MM N N=-;⑥log log (m na a nb b m m=,)n R ∈;⑦log a b a b =和log b a a b =;⑧1log log a b b a=;2、对数函数的定义及图像(1)对数函数的定义:函数log a y x =(0a >且1)a ≠叫做对数函数.对数函数的图象1a >01a <<图象性质定义域:(0)+∞,值域:R过定点(10),,即1x =时,0y =在(0)+∞,上增函数在(0)+∞,上是减函数当01x <<时,0y <,当1x ≥时,y ≥当01x <<时,0y >,当1x ≥时,0y≤【解题方法总结】1、对数函数常用技巧在同一坐标系内,当1a >时,随a 的增大,对数函数的图象愈靠近x 轴;当01a <<时,对数函数的图象随a 的增大而远离x 轴.(见下图)必考题型全归纳题型一:对数运算及对数方程、对数不等式【例1】(2024·四川成都·成都七中校考模拟预测)1ln3411e 812-+=______.【答案】1-【解析】114ln3144111e81331)33112⨯-+-+=-++=--=-.故答案为:1-【对点训练1】(2024·辽宁沈阳·沈阳二中校考模拟预测)已知lg 2a b +=-,10b a =,则=a ______.【答案】110/0.1【解析】由题设1log 10lg a b a ==,则1lg 2lg a a+=-且0a >,所以22lg 2lg 1(lg 1)0a a a ++=+=,即lg 1a =-,故110a =.故答案为:110【对点训练2】(2024·上海徐汇·位育中学校考模拟预测)方程()2lg(2)lg 3x x -=-的解集为________.【答案】{}|1x x =-【解析】因为()2lg(2)lg 3x x -=-,则22232030x x x x ⎧-=-⎪->⎨⎪->⎩,解得=1x -,所以方程()2lg(2)lg 3x x -=-的解集为{}|1x x =-.故答案为:{}|1x x =-【对点训练3】(2024·山东淄博·统考二模)设0,0p q >>,满足()469log log log 2p q p q ==+,则pq=__________.【答案】12/0.5【解析】令()469log log log 2p q p q k ==+=,则4,6,29k k k p q p q ==+=,所以22469k k kp q +=⋅+=,整理得2222133kk k ⎛⎫⎛⎫⋅+= ⎪ ⎪⎝⎭⎝⎭,解得2132k k =(负值舍去),所以421632k k k k p q ===.故答案为:12.【对点训练4】(2024·天津南开·统考二模)计算34223log 32log 9log log 64⋅-+的值为______.【答案】8【解析】原式2523223222233=log 2log 3log log 65log 2log 3log log 644⋅-+=⋅-+2222365log log 65log 5log 88344=-+=+=+=.故答案为:8.【对点训练5】(2024·全国·高三专题练习)若14log 2a =,145b =,用a ,b 表示35lo g 28=____________【答案】11ab a++-【解析】因为145b =,所以14lo g 5b=,1414143514141414log 28log 14log 21log 28log 35log 14log 5log 21ab a++===+-+-.故答案为:11ab a++-.【对点训练6】(2024·上海·高三校联考阶段练习)若123==a b m ,且112a b-=,则m =__________.【答案】2【解析】123a b m == ,且112a b-=,0m ∴>且1m ≠,123log ,log a m b m ∴==,11log 12,log 3m m a b ∴==,11log 12log 3log 42m m m a b∴-=-==,2m ∴=.故答案为:2.【对点训练7】(2024·全国·高三专题练习)()()()226622lg 3lg 2log 3log 2lg 3lg 2⋅+++=____________;【答案】1【解析】原式()()226662lg 3lg 2log 3l l lg 6g og 2⋅=⋅++()()226666log 3log 22log 3log 2=++⋅()266log 3log 2=+()26log 61==.故答案为:1.【对点训练8】(2024·全国·高三专题练习)解关于x 的不等式2)l g (o 24xx <-解集为_____.【答案】1(0,)2【解析】不等式222log 24log 24(log 2)(4)202x x x x xx -⇔--<<<<⇔,解240x ->,即222x <,有21x <,解得12x <,解224x x -<,即22220x x +->,化为2)(21)0(2x x +->,有21x >,解得0x >,因此102x <<,所以不等式2)l g (o 24xx <-解集为1(0,2.故答案为:1(0,2【对点训练9】(2024·上海杨浦·高三上海市杨浦高级中学校考开学考试)已知函数()f x 是定义在R 上的奇函数,当0x >时,()2log f x x =,则()2f x ≥-的解集是__________.【答案】][14,0,4⎡⎫-⋃+∞⎪⎢⎣⎭【解析】当0x <时,0x ->,所以()2()log f x x -=-,因为函数()f x 是定义在R 上的奇函数,所以()2()()log f x f x x =--=--,所以当0x <时,()2()log f x x =--,所以()22log ,0()0,0log ,0x x f x x x x ⎧--<⎪==⎨⎪>⎩,要解不等式()2f x ≥-,只需20log 2x x >⎧⎨≥-⎩或()20log 2x x <⎧⎨--≥-⎩或002x =⎧⎨≥-⎩,解得14x ≥或40x -≤<或0x =,综上,不等式的解集为][14,0,4∞⎡⎫-⋃+⎪⎢⎣⎭.故答案为:][14,0,4∞⎡⎫-⋃+⎪⎢⎣⎭.【对点训练10】(2024·上海浦东新·高三华师大二附中校考阶段练习)方程42log 17xx +=的解为_________.【答案】4x =【解析】设函数()42log x f x x =+,()0,x ∈+∞,由于函数42,log xy y x ==在()0,x ∈+∞上均为增函数,又()4442log 416117f =+=+=,故方程42log 17xx +=的解为4x =.故答案为:4x =.【解题方法总结】对数的有关运算问题要注意公式的顺用、逆用、变形用等.对数方程或对数不等式问题是要将其化为同底,利用对数单调性去掉对数符号,转化为不含对数的问题,但这里必须注意对数的真数为正.题型二:对数函数的图像【例2】(2024·全国·高三专题练习)已知函数()log a y x b =+(a ,b 为常数,其中0a >且1a ≠)的图象如图所示,则下列结论正确的是()A .0.5a =,2b =B .2a =,2b =C .0.5a =,0.5b =D .2a =,0.5b =【答案】D【解析】由图象可得函数在定义域上单调递增,所以1a >,排除A ,C ;又因为函数过点(0.5,0),所以0.51b +=,解得0.5b =.故选:D【对点训练11】(2024·全国·高三专题练习)函数()log (1)2a f x x =-+的图象恒过定点()A .(2,2)B .(2,1)C .(3,2)D .(2,0)【答案】A【解析】当2x =时(2)log 122a f =+=,即函数图象恒过(2,2).故选:A【对点训练12】(2024·北京·统考模拟预测)已知函数()()22log 1f x x x =--,则不等式()0f x <的解集为()A .()(),12,-∞+∞B .()()0,12,⋃+∞C .()1,2D .()1,+∞【答案】B【解析】由题意,不等式()0f x <,即()22log 10x x --<,等价于()22log 1x x <-在()0,∞+上的解,令()2log g x x =,()()21h x x =-,则不等式为()()g x h x <,在同一坐标系下作出两个函数的图象,如图所示,可得不等式()0f x <的解集为()()0,12,⋃+∞,故选:B【对点训练13】(2024·北京·高三统考学业考试)将函数2log y x =的图象向上平移1个单位长度,得到函数()y f x =的图象,则()f x =()A .()2log 1x +B .21log x +C .()2log 1x -D .21log x-+【答案】B【解析】将函数2log y x =的图象向上平移1个单位长度,得到函数21log y x =+.故选:B.【对点训练14】(2024·北京海淀·清华附中校考模拟预测)不等式32log (1)(2)0x x x --->的解集为__________.【答案】{}13x x <<【解析】由3312log (1)(2)0log (1)(2)2x x x x x x --->⇒>--,在同一直角坐标系内画出函数()()31log ,(1)(2)2f x xg x x x ==--的图象如下图所示:因为()()331f g ==,所以由函数的图象可知:当(1,3)x ∈时,有()()f x g x >,故答案为:{}13x x <<【对点训练15】(多选题)(2024·全国·高三专题练习)当102x <≤时,4log xa x ≤,则a 的值可以为()A2B .2C .3D 【答案】ABC【解析】分别记函数()4x f x =,()log a g x x =由图1知,当1a >时,不满足题意;当01a <<时,如图2,要使102x <≤时,不等式4log xa x ≤恒成立,只需满足11((22f g ≤,即1214log 2a≤,即12log 2a ≤,解得12a ≤<.故选:ABC【解题方法总结】研究和讨论题中所涉及的函数图像是解决有关函数问题最重要的思路和方法.图像问题是数和形结合的护体解释.它为研究函数问题提供了思维方向.题型三:对数函数的性质(单调性、最值(值域))【例3】(2024·全国·高三专题练习)已知函数3()log (1)f x ax =-,若()f x 在(,1]-∞上为减函数,则a 的取值范围为()A .(0,)+∞B .(0,1)C .(1,2)D .(,1)-∞【答案】B【解析】设函数1y ax =-,因为()f x 在(,1]-∞上为减函数,所以1y ax =-在(,1]-∞上为减函数,则0a -<解得0a >,又因为10y ax =->在(,1]-∞恒成立,所以min 10y a =->解得1a <,所以a 的取值范围为01a <<,故选:B.【对点训练16】(2024·新疆阿勒泰·统考三模)正数,a b 满足2224log log a bb a -=-,则a与2b 大小关系为______.【答案】2a b </2b a>【解析】因为2224log log a bb a -=-,所以22222222log 4log 2log log 212log 21a b b ba b b b +=+=++-=+-,设2()2log x f x x =+,则()(2)1f a f b =-,所以()(2)f a f b <,又因为2x y =与2log y x =在(0,)+∞上单调递增,所以2()2log x f x x =+在(0,)+∞上单调递增,所以2a b <.故答案为:2a b <.【对点训练17】(2024·全国·高三专题练习)已知函数()()log 0,1a f x x a a =>≠在[]1,4上的最大值是2,则a 等于_________【答案】2【解析】当1a >时,函数()log a f x x =在[]1,4上单调递增,则()4log 42a f ==,解得2a =,当01a <<时,函数()log a f x x =在[]1,4上单调递减,则()1log 12a f ==,无解,综上,a 等于2.故答案为:2.【对点训练18】(2024·全国·高三专题练习)若函数()log a f x x =(0a >且1a ≠)在1,42⎡⎤⎢⎥⎣⎦上的最大值为2,最小值为m ,函数()(32g x m =+[0,)+∞上是增函数,则a m -的值是____________.【答案】3【解析】当1a >时,函数()log a f x x =是正实数集上的增函数,而函数()log a f x x =在1,42⎡⎤⎢⎥⎣⎦上的最大值为2,因此有(4)log 42a f ==,解得2a =,所以21log 12m ==-,此时()g x 在[)0,∞+上是增函数,符合题意,因此()213a m -=--=;当01a <<时,函数()log a f x x =是正实数集上的减函数,而函数()log a f x x =在1,42⎡⎤⎢⎥⎣⎦上的最大值为2,因此有11log 222a f ⎛⎫== ⎪⎝⎭,2a =,所以44m ==-,此时()g x =-在[)0,∞+上是减函数,不符合题意.综上所述,2a =,1m =-,3a m -=.故答案为:3.【对点训练19】(2024·全国·高三专题练习)若函数2()log (1)a f x x ax =-+有最小值,则a的取值范围是______.【答案】()1,2【解析】当01a <<时,外层函数log a y u =为减函数,对于内层函数21u x ax =-+,240a ∆=-<,则0u >对任意的实数x 恒成立,由于二次函数21u x ax =-+有最小值,此时函数()()2log 1a f x x ax =-+没有最小值;当1a >时,外层函数log a y u =为增函数,对于内层函数21u x ax =-+,函数21u x ax =-+有最小值,若使得函数()()2log 1a f x x ax =-+有最小值,则2401a a ⎧∆=-<⎨>⎩,解得12a <<.综上所述,实数a 的取值范围是()1,2.故答案为:()1,2.【对点训练20】(2024·河南·校联考模拟预测)写出一个同时具有下列性质①②③的函数:()f x =_____.①()()()1212f x x f x f x =+;②当,()0x ∈+∞时,()f x 单调递减;③()f x 为偶函数.【答案】12log x (不唯一)【解析】性质①显然是和对数有关,性质②只需令对数的底01a <<即可,性质③只需将自变量x 加绝对值即变成偶函数.故答案为:12log x (不唯一)【对点训练21】(2024·重庆渝中·高三重庆巴蜀中学校考阶段练习)函数()214log 2y x x =--的单调递区间为()A .1,2⎛⎫-∞ ⎪⎝⎭B .(),1-∞-C .1,2⎛⎫+∞ ⎪⎝⎭D .()2,+∞【答案】B【解析】函数()214log 2y x x =--的定义域为(,1)(2,),-∞-⋃+∞令22t x x =--,又14log y t =在定义域内为减函数,故只需求函数22t x x =--在定义域()(),12,-∞-⋃+∞上的单调递减区间,又因为函数22t x x =--在(),-1∞-上单调递减,()214log 2y x x ∴=--的单调递区间为(),1-∞-.故选:B【对点训练22】(2024·陕西宝鸡·统考二模)已知函数()()lg lg 2f x x x =+-,则()A .()f x 在()0,1单调递减,在()1,2单调递增B .()f x 在()0,2单调递减C .()f x 的图像关于直线1x =对称D .()f x 有最小值,但无最大值【答案】C【解析】由题意可得函数()()lg lg 2f x x x =+-的定义域为(0,2),则()()2lg lg 2lg(2)f x x x x x =+-=-+,因为22y xx =-+在(0,1)上单调递增,在(1,2)上单调递减,且lg y x =在(0,)+∞上单调递增,故()f x 在(0,1)上单调递增,在(1,2)上单调递减,A ,B 错误;由于()2lg(2)lg ()f x x x f x -=-+=,故()f x 的图像关于直线1x =对称,C 正确;因为22y xx =-+在1x =时取得最大值,且lg y x =在(0,)+∞上单调递增,故()f x 有最大值,但无最小值,D 错误,故选:C【对点训练23】(2024·全国·高三专题练习)若函数2,1,()2log ,1x a a x f x a x x ⎧+≤=⎨+>⎩在R 上单调,则a 的取值范围是()A .()0,1B .[2,)+∞C .10,(2,)2⎛⎫+∞ ⎪⎝⎭D .()0,1[2,)⋃+∞【答案】D【解析】若()f x 在R 上单调递增,则122log 1a a a a >⎧⎨+≤+⎩,解得[2,)a ∈+∞,若()f x 在R 上单调递减,则0122log 1a a a a <<⎧⎨+≥+⎩,解得(0,1)a ∈.综上得(0,1)[2,)a ∈+∞ .故选:D【解题方法总结】研究和讨论题中所涉及的函数性质是解决有关函数问题最重要的思路和方法.性质问题是数和形结合的护体解释.它为研究函数问题提供了思维方向.题型四:对数函数中的恒成立问题【例4】(2024·全国·高三专题练习)已知函数()29x f x x +=,()2log g x x a =+,若存在[]13,4x ∈,任意[]24,8x ∈,使得()()12f x g x ≥,则实数a 的取值范围是___________.【答案】13,4∞⎛⎤- ⎥⎝⎦【解析】若()f x 在[3,4]上的最大值max ()f x ,()g x 在[4,8]上的最大值max ()g x ,由题设,只需max max ()()f x g x ≥即可.在[3,4]上,9()6f x x x =+≥=当且仅当3x =时等号成立,由对勾函数的性质:()f x 在[3,4]上递增,故max 25()4f x =.在[4,8]上,()g x 单调递增,则max ()3g x a =+,所以2534a ≥+,可得134a ≤.故答案为:13,4∞⎛⎤- ⎥⎝⎦.【对点训练24】(2024·全国·高三专题练习)若1,22x ⎡⎤∀∈⎢⎥⎣⎦,不等式2122log 0x x x ax -+<恒成立,则实数a 的取值范围为___________.【答案】(),5-∞-【解析】因为1,22x ⎡⎤∀∈⎢⎥⎣⎦,不等式2122log 0x x x ax -+<恒成立,所以12log 2a x x <-对1,22x ⎡⎤∀∈⎢⎥⎣⎦恒成立.记()12log 2f x x x =-,1,22x ⎡⎤∈⎢⎥⎣⎦,只需()min a f x <.因为12log y x =在1,22x ⎡⎤∈⎢⎥⎣⎦上单调递减,2y x =-在1,22x ⎡⎤∈⎢⎥⎣⎦上单调递减,所以()12log 2f x x x =-在1,22x ⎡⎤∈⎢⎥⎣⎦上单调递减,所以()()min 25f x f ==-,所以5a <-.故答案为:(),5-∞-【对点训练25】(2024·全国·高三专题练习)已知函数2()23=-+f x x x ,2()log g x x m =+,对任意的1x ,2[1x ∈,4]有12()()f x g x >恒成立,则实数m 的取值范围是___________.【答案】(,0)-∞【解析】函数22()23(1)2=-+=-+f x x x x 在[1,4]上单调递增,2()log g x x m =+在[1,4]上单调递增,∴()()min 12f x f ==,()()max 42g x g m ==+,对任意的1x ,2[1x ∈,4]有12()()f x g x >恒成立,∴()()min max f x g x >,即22m >+,解得0m <,∴实数m 的取值范围是(),0∞-.故答案为:(,0)-∞.【对点训练26】(2024·全国·高三专题练习)已知函数()()2223,log f x x x g x x m =-+=+,若对[][]122,4,16,32x x ∀∈∃∈,使得()()12f x g x ,则实数m 的取值范围为___________.【答案】(],1-∞-【解析】因为对[][]122,4,16,32x x ∀∈∃∈,使得()()12f x g x ≥,所以()()12min min f x g x ≥,因为()223x x x f =-+的对称轴为1x =,所以()f x 在[]2,4上单调递增,所以()()min 23f x f ==,又因为()2log g x x m =+在[]16,32上单调递增,所以()()min 164g x g m ==+,所以34m ≥+,所以1m ≤-,即(],1m ∈-∞-,故答案为:(],1-∞-.【对点训练27】(2024·全国·高三专题练习)已知函数()()()2log 2log 30,1a a f x x x a a =++>≠.(1)若()32f =,求a 的值;(2)若对任意的[]8,12x ∈,()6f x >恒成立,求a 的取值范围.【解析】(1)因为()32f =,所以()2log 32log 332a a ++=,所以()2log 310a +=,所以log 31a =-,解得13a =.(2)由()6f x >,得()2log 2log 30a a x x +->,即()()log 3log 10a a x x +->,即log 3a x <-或log 1>a x .当01a <<时,log 12log log 8a a a x ≤≤,则log 83a <-或log 121a >,因为log 12log 10a a <=,则log 121a >不成立,由log 83a <-可得318a ⎛⎫< ⎪⎝⎭,得112a <<;当1a >时,log 8log log 12a a a x ≤≤,则log 123a <-或log 81a >,因为log 12log 10a a >=,则log 123a <-不成立,所以log 81a >,解得18a <<.综上,a 的取值范围是()1,11,82⎛⎫⋃ ⎪⎝⎭.【对点训练28】(2024·全国·高三专题练习)已知2()32log f x x =-,2()log g x x =.(1)当[]1,4x ∈时,求函数[]()1()y f x g x =+⋅的值域;(2)对任意12,2n n x +⎡⎤∈⎣⎦,其中常数n N ∈,不等式()2()f x f kg x ⋅>恒成立,求实数k 的取值范围.【解析】(1)因为2()32log f x x =-,2()log g x x =,[]()1()y f x g x =+⋅令()()()222242log log 2log 12y h x x x x ==-⋅=--+,∵[]1,4x ∈,∴[]2log 0,2x ∈,所以当2log 1x =,即2x =时取最大值()max 2h x =,当2log 0x =或2,即1x =或4x =时取最小值()min 0h x =,∴函数()h x 的值域为[]0,2.(2)由()()2f x fk g x ⋅>⋅得()()22234log 3log logx x k x -->⋅,令2log t x =,∵12,2n n x +⎡⎤∈⎣⎦,∴[]2log ,1t x n n =∈+,∴()()343t t k t -->⋅对一切的[],1t n n ∈+恒成立,①当0n =时,若0=t 时,R k ∈;当(]0,1t ∈时,()()343t t k t--<恒成立,即9415k t t<+-,函数9415t t+-在(]0,1t ∈单调递减,于是1t =时取最小值-2,此时2x =,于是(),2k ∈-∞-;②当1n =时,此时[]1,2t ∈时,()()343t t k t--<恒成立,即9415k t t<+-,∵9412t t +≥,当且仅当94t t =,即32t =时取等号,即9415t t+-的最小值为-3,(),3k ∈-∞-;③当2n ≥时,此时[],1t n n ∈+时,()()343 t t k t--<恒成立,即9415k t t<+-,函数9415t t +-在[],1t n n ∈+单调递增,于是t n =时取最小值9415n n-+,此时2n x =,于是9,415k n n ⎛⎫∈-∞-+ ⎝⎭.综上可得:当0n =时(),2k ∈-∞-,当1n =时(),3k ∈-∞-,当2n ≥时,9,415k n n ⎛⎫∈-∞-+⎪⎝⎭【解题方法总结】(1)利用数形结合思想,结合对数函数的图像求解;(2)分离自变量与参变量,利用等价转化思想,转化为函数的最值问题.(3)涉及不等式恒成立问题,将给定不等式等价转化,借助同构思想构造函数,利用导数探求函数单调性、最值是解决问题的关键.题型五:对数函数的综合问题【例5】(多选题)(2024·湖北·黄冈中学校联考模拟预测)已知1a >,1b >,21a aa =-,2log 1bb b =-,则以下结论正确的是()A .22log aa b b+=+B .21112log ab+=C .2a b -<-D .4a b +>【答案】ABD【解析】对于A ,由题意知,a ,b 是函数1()111x h x x x ==+--分别与函数()2x f x =,2()log g x x =图象交点的横坐标,由1y x=的图象关于y x =对称,则其向上,向右都平移一个单位后的解析式为1()11h x x =+-,所以()h x 的图象也关于y x =对称,又()f x ,()g x 两个函数的图象关于直线y x =对称,故两交点(),2aa ,()2,logb b 关于直线y x =对称,所以2log a b =,2a b =,故A 正确;对于B ,结合选项A 得21aa b a ==-,则ab a b =+,即111a b +=,即21112log a b +=成立,故B 正确;对于C ,结合选项A 得2log (24)a b b b b -=-<<,令2()log b b b ϕ=-,则1()10ln 2b b ϕ'=-<,所以2()log b b b ϕ=-在(2,4)上单调递减,则2()log 442b ϕ>-=-,故C 错误;对于D ,结合选项B 得11()24b aa b a b a b a b⎛⎫+=++=++> ⎪⎝⎭(a b¹,即不等式取不到等号),故D 正确.故选:ABD.【对点训练29】(2024·海南海口·统考模拟预测)已知正实数m ,n 满足:ln e ln m n n n m =-,则nm的最小值为______.【答案】2e 4【解析】由ln e ln mn n n m =-可得:e ln ln mm n n=+,所以ln e ln ln m n n m --=,ln ln e ln ln e ln m n m m n m m m -+-=+=+,设()e x f x x =+,()e 10xf x '=+>,所以()f x 在R 上单调递增,所以()()ln ln f m n f m -=,则ln ln m n m -=,所以e ln ln mn m=,所以e m n m =,所以2e m n m m =,令()()()2243e 2e e e 2,xx x x x x x g x g x x x x-⋅-⋅=='=,令()0g x '>,解得:2x >;令()0g x '<,解得:02x <<;所以()g x 在()0,2上单调递减,在()2,+∞上单调递增,所以()()2mine 24g x g ==.故n m 的最小值为2e 4.故答案为:2e 4.【对点训练30】(多选题)(2024·广东惠州·统考一模)若62,63a b ==,则()A .1ba>B .14ab <C .2212+<a b D .15b a ->【答案】ABD【解析】因为63,62b a ==,所以66log 3,log 2b a ==,则1a b +=,选项A ,6226log 3log 3log 21log 2b a ==>=,故A 正确;选项B ,因为666log 3log 2log 61a b +=+==,且0,0,a b a b >>≠,所以21()24a b ab +<=,故B 正确;选项C ,因为22211()2121242a b a b ab ab +=+-=->-⨯=,故C 错误;选项D ,因为()666324355log log log 61232b a -==>=,故D 正确,故选:ABD .【对点训练31】(2024·河南·高三信阳高中校联考阶段练习)已知1x ,2x 分别是方程e 3x x +=和ln 3x x +=的根,若12x x a b +=+,实数a ,0b >,则271b ab+的最小值为()A .1B .73C .679D .2【答案】D【解析】e 3,e 3x x x x +==-;ln 3,ln 3x x x x +==-.函数e x y =与函数ln y x =的图象关于直线y x =对称,由3y x y x=-⎧⎨=⎩解得32x y ==,设33,22A ⎛⎫⎪⎝⎭,则123232x x +=⨯=,即3a b +=,()()22222273211717171333b b b b b b ab b b b bb b -+++++==-=----221173b b b +⎛⎫=-+ ⎪-⎝⎭,令211b t +=,则121t b -=,则222712117731132121b b t ab b b t t ⎛⎫ ⎪++⎛⎫ ⎪=-+=-+ ⎪ ⎪-⎝⎭--⎛⎫-⨯ ⎪ ⎪⎝⎭⎝⎭4417726465t t ⎛⎫⎛⎫⎪ ⎪ =-+≥-= ⎪ ⎪+- ⎝⎭⎝,当且仅当6418,8211,,333t t b b a b t ===+==-=时等号成立.故选:D【对点训练32】(2024·全国·高三专题练习)若1x 满足25x x =-,2x 满足2log 5x x +=,则12x x +等于()A .2B .3C .4D .5【答案】D【解析】由题意1152xx -=,故有2225log x x -=故1x 和2x 是直线5y x =-和曲线2x y =、曲线2log y x =交点的横坐标.根据函数2x y =和函数2log y x =互为反函数,它们的图象关于直线y x =对称,故曲线2x y =和曲线2log y x =的图象交点关于直线y x =对称.即点(x 1,5﹣x 1)和点(x 2,5﹣x 2)构成的线段的中点在直线y =x 上,即12125522x x x x +-+-=,求得x 1+x 2=5,故选:D.【对点训练33】(2024·全国·高三专题练习)已知1x 是方程32x x ⋅=的根,2x 是方程3log 2x x ⋅=的根,则12x x ⋅的值为()A .2B .3C .6D .10【答案】A【解析】方程32x x ⋅=可变形为方程23x x =,方程3log 2x x ⋅=可变形为方程3log 2x x=,1x 是方程32x x ⋅=的根,2x 是方程3log 2x x ⋅=的根,2025高考数学必刷题1x ∴是函数3x y =与函数2y x =的交点横坐标,2x 是函数3log y x ==与函数2y x =的交点横坐标, 函数3x y =与函数3log y x =互为反函数,∴函数3log y x =与函数2y x =的交点横坐标2x 等于函数3x y =与函数2y x =的交点纵坐标,即12(,)x x 在数2y x =图象上,又2y x = 图象上点的横纵坐标之积为2,122x x ∴=,故选:A。
对数平均值的几何解释与探究(岳峻)

三、不等式链的证明
评注:涉及两个变量的不等式的证明,其解题策略耐人 寻味: 证法1是先将不等式逆推分析,进行等价转化,使得其 中的两个变量的特征、规律更明朗,然后将两个变量的比值 (或和、或差、或积)替换为新的一元变量,便于构造出新 的一元函数,再通过对新的一元函数求导,判断其单调性、 确定极值(或最值),达到解决问题的目的,可归结为 “化归-换元-构造-求导”; 证法2将地位均衡的两个变量之一作为主元,另外的一 个变量视为常量来处理,构造出一元函数,可归结为 “化归-主元-构造-求导”.
高考压轴题与对数平均值
一、对数平均值的概念
中学数学教育专家安振平在剖析2013年 陕西高考数学时指出,其压轴题的理论背景 是: 设 a, b 0, 则
ab a b ab 2 ln a ln b
其中
,
a b ln a ln b
被称之为对数平均值.
一、对数平均值的概念
对数平均值在现行高中教材没有出现, 但其蕴含着高等数学的背景,近几年的高考 压轴题中,频频出现。 安振平老师构造函数,借助于导数证明 了对数平均数的有关不等式,难度较大,为 此,本人作了一些探讨,以期对2016年的复 习迎考有所启发。
三、不等式链的证明
设函数 f x 1 x ln x 2 x 1 x 1 , 则
证法1:设 b a 0, a b ,则不等式等价于 骣 骣 b 鼢 b b 珑 1鼢 ln > 2 - 1 (a + b)(ln b - ln a) > 2(b - a) ? 珑 鼢 珑 桫 桫 a a a
ab
四、对数平均值的几何解释
(3)又 S矩形ABQX < S曲边梯形ABQP < S梯形ABQP , < S矩形ABYP , 1 1骣 1 1÷ 1 ç + ÷ (b - a) < (b - a),L ③ 所以 b (b - a) < ln b - ln a < 2 ç ÷ ç 桫 a b a
2023年高考数学二轮复习 第1部分 专题突破 专题1 培优点2 对数平均不等式、切线不等式

由对数平均不等式知 ln
x1-x2 x1-ln
x2>
x1x2=1,
又x2>x1>0, ∴x1-x2<0,ln x1-ln x2<0,
∴0<ln
x1-ln x1-x2
x2<1,
∴fxx11- -xf2x2=-2+alnxx11--xl2n x2<-2+a,
即证原不等式成立.
考点二
以泰勒公式为背景的切线不等式
(1)当a>0时,求函数f(x)的单调递增区间;
f(x)的定义域为(0,+∞), f′(x)=ax-(2a+1)+2x=ax-1xx-2, 当 0<1a<2,即 a>12时,在0,1a和(2,+∞)上,f′(x)>0,f(x)单调递增;
当1a=2,即 a=12时,f′(x)≥0,f(x)在(0,+∞)上单调递增; 当1a>2,即 0<a<12时,在(0,2)和1a,+∞上,f′(x)>0,f(x)单调递增. 综上所述,当 a>12时,f(x)的单调递增区间为0,1a和(2,+∞);
即eex≥x,ex≥ex,当 x=1 时等号成立,
即e-ln x≥e(-ln x),
所以1x≥e(-ln x), 即 ln x≥-e1x,当 x=1e时等号成立,
所以
exln
x+e2x≥ex-e1x+e2x=eexx >1(等号不同时成立).
方法二 由(1)知,f(x)=exln x+2eexx, 从而 f(x)>1 等价于 xln x>exx-2e. 设函数g(x)=xln x,则g′(x)=1+ln x.
构造函数 f(t)=2ln t-t+1t (t>1), 则 f′(t)=2t -1-t12=-t-t212<0,
利用对数平均不等式巧解一类数学压轴题

利用对数平均不等式巧解一类数学压轴题作者:行凯歌
来源:《新高考·高一数学》2018年第05期
基本不等式是高中数学中的重要内容,它往往和函数、导数、最值等聯系紧密,对学生的逻辑思维能力要求很高,倍受高考命题者的青睐.几何平均、算术平均是我们熟知的两个概念,对数平均虽然在教材中未提及,但是却在高考压轴题和各地模拟题中频频m现,因此,同学们要高度重视.如果以函数思想为指导,把一类双变量齐次函数问题转化为一元函数问题,再用导数为T具就能有效解决,而这个转化的思想就蕴含在对数平均不等式的证明之中.
一、知识介绍——对数平均不等式及证明
二、推广变形——对数平均不等式的常见变形形式
总之,与“对数平均”有关的证明题,常以压轴题的最后一问出现,综合性强,难度较高.同学们在解题时应简化思路与计算,领悟构造函数法在高考数学证明题中的无穷魅力,。
利用对数平均不等式破解极值点偏移问题

龙源期刊网
利用对数平均不等式破解极值点偏移问题
作者:杨瑞强
来源:《中学数学杂志(高中版)》2016年第05期
近几年的高考数学压轴题中,经常出现与函数的极值点偏移有关的问题,由于这类问题的解决往往需要构造函数,技巧性较强,考生难于切入,在短时间内难以解决.如果我们借助对数平均不等式加以放缩,那么问题难度大大降低.下面谈谈利用这个不等式破解此类高考导数的压轴题.
1极值点偏移的定义
对于函数y=f(x)在区间(a,b)内只有一个极值点x0,方程f(x)=0的解为x1,x2,且a
(1)若x1+x22>x0,则称函数y=f(x)在区间(a,b)上极值点x0左偏,简称x0左偏;(2)若x1+x22
4转化策略与步骤
极值点偏移问题中,函数中多有形如ex和lnx的式子,并且极值点偏移问题实质是双变量的问题,而双变量的问题许多都可以回归对数平均.常利用对数平均不等式放缩解决,其转化的步骤有:
第一步:根据f(x1)=f(x2)建立等式;
第二步:如果等式含有参数,则消参;有指数的则两边取对数,转化为对数式;
第三步:通过恒等变换转化为对数平均问题,利用对数平均不等式放缩求解.
作者简介杨瑞强(1979—),男,湖北黄冈人,中学一级教师,黄石市优秀班主任,黄石市优秀数学教师,主要从事数学教育与中学教学研究.近几年,在数学专业杂志上发表文章80余篇.。
2023年数学高考复习真题演练(2021-2022年高考真题)10 对数与对数函数 (含详解)

专题10 对数与对数函数【考点预测】 1.对数式的运算(1)对数的定义:一般地,如果(0x a N a =>且1)a ≠,那么数x 叫做以a 为底N 的对数,记作log a x N =,读作以a 为底N 的对数,其中a 叫做对数的底数,N 叫做真数.(2)常见对数:①一般对数:以(0a a >且1)a ≠为底,记为log N a ,读作以a 为底N 的对数;②常用对数:以10为底,记为lg N ; ③自然对数:以e 为底,记为ln N ; (3) 对数的性质和运算法则:①1log 0a =;log 1a a =;其中0a >且1a ≠;②log Na a N =(其中0a >且1a ≠,0N >); ③对数换底公式:log log log c a c bb a=; ④log ()log log a a a MN M N =+; ⑤log log log aa a MM N N=-; ⑥log log (m na a nb b m m=,)n R ∈; ⑦log a b a b =和log b a a b =; ⑧1log log a b b a=; 2.对数函数的定义及图像(1)对数函数的定义:函数 log a y x =(0a >且1)a ≠叫做对数函数. 对数函数的图象【方法技巧与总结】 1.对数函数常用技巧在同一坐标系内,当1a >时,随a 的增大,对数函数的图象愈靠近x 轴;当01a <<时,对数函数的图象随a 的增大而远离x 轴.(见下图)【题型归纳目录】题型一:对数运算及对数方程、对数不等式 题型二:对数函数的图像题型三:对数函数的性质(单调性、最值(值域)) 题型四:对数函数中的恒成立问题 题型五:对数函数的综合问题 【典例例题】题型一:对数运算及对数方程、对数不等式例1.(2022·全国·高三专题练习)(1)计算331log 2327lg 50lg 2+++; (2)已知()23log log lg 1x ⎡⎤=⎣⎦,求实数x 的值; (3)若185a =,18log 9b =,用a ,b ,表示36log 45. 例2.(2022·全国·高三专题练习)(1)求23151log log 8log 2725⋅⋅的值. (2)已知9log 5=a ,37b =,试用a ,b 表示21log 35例3.(2022·全国·高三专题练习)(1)已知a ,b ,c 均为正数,且3a =4b =6c ,求证:212ab c+=;(2)若60a =3,60b =5,求12(1)12a bb ---的值.例4.(2022·全国·模拟预测)若e 4a =,e 25b =,则( ) A .a +b =100B .b -a =ea 增大a 增大C .28ln 2ab <D .ln6b a ->例5.(2022·全国·模拟预测)已知实数x ,y 满足0x >,0y >,1x ≠,1y ≠,y x x y =,log 4y xx y+=,则x y +=( ) A .2 B .4 C .6 D .8例6.(2022·北京昌平·二模)已知函数2()42(0)f x ax ax a =-+<,则关于x 的不等式2()log f x x >的解集是( )A .(,4)-∞B .(0,1)C .(0,4)D .(4,)+∞例7.(2022·全国·江西师大附中模拟预测(文))已知函数()122log ,1,1,1,x x f x x x >⎧⎪=⎨⎪-≤⎩则不等式()(1)f x f x <-的解集为______.例8.(2022·辽宁·东北育才学校二模)若函数()f x 满足:(1)1x ∀,()20,x ∈+∞且12x x ≠,都有()()21210f x f x x x -<-;(2)()()1122x f f x f x x ⎛⎫=- ⎪⎝⎭,则()f x =___________.(写出满足这些条件的一个函数即可)例9.(2022·全国·高三专题练习)设函数()log m f x x =(0m >且1m ≠)的图像经过点()3,1.(1)解关于x 的方程()()22(1)10f x m f x m +-+-=;(2)不等式()()10f x a f x +⋅->⎡⎤⎡⎤⎣⎦⎣⎦的解集是1,93⎛⎫⎪⎝⎭,试求实数a 的值.【方法技巧与总结】对数的有关运算问题要注意公式的顺用、逆用、变形用等.对数方程或对数不等式问题是要将其化为同底,利用对数单调性去掉对数符号,转化为不含对数的问题,但这里必须注意对数的真数为正.题型二:对数函数的图像例10.(2022·山东潍坊·二模)已知函数()()log a f x x b =-(0a >且1a ≠)的图像如图所示,则以下说法正确的是( )A .0a b +<B .1ab <- C .01b a << D .log 0a b >例11.(2022·江苏省高邮中学高三阶段练习)函数log (3)1(0a y x a =+->且1)a ≠的图象恒过定点A ,若点A 在直线10mx ny ++=上,其中0mn >,则11+m n的最小值为( ) A .3-B .1C . 3+D .2+(多选题)例12.(2022·福建·莆田二中模拟预测)已知函数()()log a g x x k =+(0a >且1a ≠)的图象如下所示.函数()()1x x f x k a a -=--的图象上有两个不同的点()11,A x y ,()22,B x y ,则( )A .1a >,2k >B .()f x 在R 上是奇函数C .()f x 在R 上是单调递增函数D .当0x ≥时,()()22f x f x ≤例13.(2022·全国·高三专题练习)已知223,20(){1ln ,021x x x f x x x -+-≤<=≤≤+,若()()g x f x ax a =--的图象与x 轴有3个不同的交点,则实数a 的取值范围为______.【方法技巧与总结】研究和讨论题中所涉及的函数图像是解决有关函数问题最重要的思路和方法.图像问题是数和形结合的护体解释.它为研究函数问题提供了思维方向.题型三:对数函数的性质(单调性、最值(值域))例14.(2022·陕西·榆林市第十中学高二期中(文))函数()22log 43y x x =+-的一个单调增区间是( )A .3,2⎛⎫-∞ ⎪⎝⎭B .3,2∞⎡⎫+⎪⎢⎣⎭C .31,2⎛⎫- ⎪⎝⎭D .3,42⎡⎫⎪⎢⎣⎭例15.(2022·天津·南开中学二模)已知函数()21,14log 1,1a ax x x f x x x ⎧--≤⎪=⎨⎪->⎩是R 上的单调函数,则实数a 的取值范围为( ) A .11,42⎡⎫⎪⎢⎣⎭B .11,42⎡⎤⎢⎥⎣⎦C .10,2⎛⎤ ⎥⎝⎦D .1,12⎛⎫ ⎪⎝⎭例16.(2022·浙江·模拟预测)己知实数,(1,)∈+∞a b ,且33log log 3log log 4b a a b +=+,则( ) Ab a <<B.b a <Ca b <D.a b <<例17.(2022·全国·高三专题练习(理))函数f (x )=log ax (0<a <1)在[a 2,a ]上的最大值是( ) A .0 B .1C .2D .a 例18.(2022·重庆·模拟预测)若函数()2()log 341a f x x ax =-+-有最小值,则实数a 的取值范围是( )A.⎫⎪⎪⎝⎭B.C.⎛ ⎝⎭D.)+∞【方法技巧与总结】研究和讨论题中所涉及的函数性质是解决有关函数问题最重要的思路和方法.性质问题是数和形结合的护体解释.它为研究函数问题提供了思维方向.题型四:对数函数中的恒成立问题例19.(2022·北京·高三专题练习)若不等式2log 0a x x -<在10,2⎛⎫ ⎪⎝⎭内恒成立,则a 的取值范围是( ) A .1116a ≤< B .1116a << C .1016a <≤D .1016a <<例20.(2022·江苏·高三专题练习)已知函数22414ax x y -+⎛⎫= ⎪⎝⎭的值域为10,16⎛⎤⎥⎝⎦,若不等式()()log 4log 2x a x a t t ⋅<-在[]1,2x ∈上恒成立,则t 的取值范围是( ) A .2,25⎛⎫ ⎪⎝⎭B .2,5⎛⎫+∞ ⎪⎝⎭C .(,2)-∞D .()0,2例21.(2022·浙江·高三阶段练习)已知函数()29x f x x+=,()2log g x x a =+,若存在[]13,4x ∈,任意[]24,8x ∈,使得()()12f x g x ≥,则实数a 的取值范围是___________. 例22.(2022·全国·高三专题练习)已知函数()ln f x x x =-,已知实数0a >,若2()e ln 0x f x a a ++≥在()0+∞,上恒成立,求实数a 的取值范围. 例23.(2022·全国·高三专题练习)已知函数()log (0,1)x a f x a x a a =+>≠在[1,2]上的最大值与最小值之和为6log 2a +. (1)求实数a 的值;(2)对于任意的[2,)x ∈+∞,不等式()10kf x -≥恒成立,求实数k 的取值范围.例24.(2022·陕西安康·高三期末(文))已知函数()()()2log 2log 30,1a a f x x x a a =++>≠.(1)若()32f =,求a 的值;(2)若对任意的[]8,12x ∈,()6f x >恒成立,求a 的取值范围.例25.(2022·上海·高三专题练习)已知2()32log f x x =-,2()log g x x =. (1)当[]1,4x ∈时,求函数[]()1()y f x g x =+⋅的值域;(2)对任意12,2n n x +⎡⎤∈⎣⎦,其中常数n N ∈,不等式()2()f x f kg x ⋅>恒成立,求实数k的取值范围.【方法技巧与总结】(1)利用数形结合思想,结合对数函数的图像求解;(2)分离自变量与参变量,利用等价转化思想,转化为函数的最值问题.(3)涉及不等式恒成立问题,将给定不等式等价转化,借助同构思想构造函数,利用导数探求函数单调性、最值是解决问题的关键.题型五:对数函数的综合问题例26.(2022·河北·张家口市第一中学高三阶段练习)已知定义域为()0,∞+的单调递增函数()f x 满足:()0,x ∀∈+∞,有()()ln 1f f x x -=,则方程()242f x x x =-+-的解的个数为( )A .3B .2C .1D .0例27.(2022·四川雅安·三模(文))设()f x 是定义在R 上的偶函数,对任意R x ∈,都有()()4f x f x +=,且当[]2,0x ∈-时,()163xf x ⎛⎫=- ⎪⎝⎭.若在区间(]2,6-内关于x 的方程()()()log 201a f x x a -+=>恰有3个不同的实数根,则a 的取值范围是( ).A .()1,2B .()2,+∞C .(D .)2例28.(2022·广西柳州·高一期中)已知0a b >>,且1a b +=,则( )A.sin sin a b > B .11a b> C .22a b +>D .lg lg 0a b +=例29.(2022·河北保定·二模)已知函数2332xxy =-在()0,∞+上先增后减,函数3443xxy =-在()0,∞+上先增后减.若()231log log x =()321log log 0x a =>,()()242422log log log log x x b ==,()()343433log log log log 0x x c ==>,则( ) A .a c <B .b a <C .c a <D .a b <例30.(2022·广东·三模)已知,R a b ∈,e 是自然对数的底,若e ln b b a a +=+,则a b的取值可以是( ) A .1B .2C .3D .4例31.(2022·全国·高三专题练习)已知0x 是函数()22e ln 2x f x x x -=+-的零点,则020e ln xx -+=_______.【过关测试】一、单选题 1.(2022·辽宁辽阳·二模)区块链作为一种新型的技术,被应用于许多领域.在区块链技术中,某个密码的长度设定为512B ,则密码一共有5122种可能,为了破解该密码,在最坏的情况下,需要进行5122次运算.现在有一台计算机,每秒能进行142.510⨯次运算,那么在最坏的情况下,这台计算机破译该密码所需的时间大约为(参考数据lg20.3≈ 1.58≈)( ) A .1393.1610s ⨯ B .1391.5810s ⨯ C .1401.5810s ⨯D .1403.1610s ⨯2.(2022·山东·肥城市教学研究中心模拟预测)已知1log 3m p =,9p n =,其中0m >且1m ≠,0n >且1n ≠,若20m n -=,则p 的值为( ) A .3log 2B .2log 3C .2D .33.(2022·河南安阳·模拟预测(文))已知正实数x ,y ,z 满足(34zx y ==,则( ) A .111x y z+=B .111y z x+= C .112x y z += D .112x z y+=4.(2022·河南·南阳中学高三阶段练习(文))已知函数()()()ln 22ln 33f x x x =++-,则()f x ( )A .是奇函数,且在0,1上单调递增B .是奇函数,且在0,1上单调递减C .是偶函数,且在0,1上单调递增D .是偶函数,且在0,1上单调递减5.(2022·全国·高三专题练习)函数()log (1)2a f x x =-+的图象恒过定点 A .(2,2)B .(2,1)C .(3,2)D .(2,0)6.(2022·安徽六安·一模(文))设函数()2f x =()()2ln 41g x ax x =-+,若对任意的1R x ∈,都存在实数2x ,使得()()12f x g x =成立,则实数a 的取值范围为( ) A .(],4-∞B .(]0,4C .[]0,4D .(]0,27.(2022·湖北·荆门市龙泉中学二模)设0a >且1a ≠,sin cos a x x x >+对(0,)4x π∈恒成立,则a 的取值范围是( ) A .(0,)4πB .(0,]4πC .(,1)(1,)42ππ⋃D .[,1)4π8.(2022·浙江·模拟预测)己知实数,(1,)∈+∞a b ,且33log log 3log log 4b a a b +=+,则( )A b a <<B .b a <C a b <D .a b <<二、多选题9.(2022·重庆市天星桥中学一模)已知0,0a b >>,且1a b +=,则下列结论正确的是( ) A .11a b+的最小值是4 B .1ab ab+的最小值是2C .22a b +的最小值是D .22log log a b +的最小值是2-10.(2022·广东汕头·二模)设a ,b ,c 都是正数,且469a b c ==,则下列结论正确的是( ) A .2ab bc ac +=B .ab bc ac +=C .4949b b a c ⋅=⋅D .121c b a=-11.(2022·河北·高三阶段练习)下列函数中,存在实数a ,使函数()f x 为奇函数的是( )A .()(lg f x x =B .()2f x x ax =+C .()21xaf x e =-- D .()()2ln 2xx f x x e a =+-12.(2022·江苏·南京师大附中高三开学考试)当102x <≤时,4log xa x ≤,则a 的值可以为( )AB C D三、填空题13.(2022·天津·二模)已知()4log 41log x y +=+2x y +的最小值为__________.14.(2022·全国·高三专题练习)已知23e ln 3x x x -+=,则3e ln x x -+=__________.15.(2022·河南·模拟预测(文))已知函数()241,1log ,1x x f x x x ⎧-≤=⎨>⎩,若1()2f a <≤,则实数a的取值范围为___________.16.(2022·河南·开封高中模拟预测(文))已知函数()y f x =为奇函数,且对定义域内的任意x 都有()()11f x f x +=--.当()1,2x ∈时,()21log f x x =-.给出以下4个结论: ①函数()y f x =的图象关于点()(),0k k ∈Z 成中心对称;②函数()y f x =是以2为周期的周期函数;③当()0,1x ∈时,()()2log 21f x x =--; ④函数()y f x =在()(),1k k k +∈Z 上单调递减. 其中所有正确结论的序号为______. 四、解答题17.(2022·北京·高三专题练习)已知函数()log (0),1)a f x x a a =>≠且,设1a >,函数log a y x =的定义域为[m ,n ] (m <n ),值域为[0,1],定义“区间[m ,n ]的长度等于n -m ”,若区间[m ,n ]长度的最小值...为5,6求实数a 的值;18.(2022·全国·高三专题练习(理))已知函数f (x )=log a (x +1)-log a (1-x ),a >0且a ≠1. (1)求f (x )的定义域;(2)判断f (x )的奇偶性并予以证明; (3)当a >1时,求使f (x )>0的x 的解集.19.(2022·北京·高三专题练习)已知函数()log (0)1)a f x x a a =>≠且,作出|()|y f x =的大致图像并写出它的单调性;20.(2022·全国·高三专题练习)已知函数()()44log 3log 4f x x x =-⋅.当1,164x ⎡⎤∈⎢⎥⎣⎦时,求该函数的值域;21.(2022·全国·高三专题练习)已知:函数()0.51log 1axf x x -=-在其定义域上是奇函数,a 为常数. (1)求a 的值.(2)证明:()f x 在()1,+∞上是增函数.(3)若对于[]3,4上的每一个x 的值,不等式()12xf x m ⎛⎫>+ ⎪⎝⎭恒成立,求实数m 的取值范围.22.(2022·北京东城·高三期末)曲线ln y x =在点(,ln )A t t 处的切线l 交x 轴于点M . (1)当t e =时,求切线l 的方程;(2)O为坐标原点,记AMO的面积为S,求面积S以t为自变量的函数解析式,写出其定义域,并求单调增区间.专题10 对数与对数函数【考点预测】 1.对数式的运算(1)对数的定义:一般地,如果(0x a N a =>且1)a ≠,那么数x 叫做以a 为底N 的对数,记作log a x N =,读作以a 为底N 的对数,其中a 叫做对数的底数,N 叫做真数.(2)常见对数:①一般对数:以(0a a >且1)a ≠为底,记为log N a ,读作以a 为底N 的对数;②常用对数:以10为底,记为lg N ; ③自然对数:以e 为底,记为ln N ; (3) 对数的性质和运算法则:①1log 0a =;log 1a a =;其中0a >且1a ≠;②log Na a N =(其中0a >且1a ≠,0N >); ③对数换底公式:log log log c a c bb a=; ④log ()log log a a a MN M N =+; ⑤log log log aa a MM N N=-; ⑥log log (m na a nb b m m=,)n R ∈; ⑦log a b a b =和log b a a b =; ⑧1log log a b b a=; 2.对数函数的定义及图像(1)对数函数的定义:函数 log a y x =(0a >且1)a ≠叫做对数函数. 对数函数的图象【方法技巧与总结】 1.对数函数常用技巧在同一坐标系内,当1a >时,随a 的增大,对数函数的图象愈靠近x 轴;当01a <<时,对数函数的图象随a 的增大而远离x 轴.(见下图)【题型归纳目录】题型一:对数运算及对数方程、对数不等式 题型二:对数函数的图像题型三:对数函数的性质(单调性、最值(值域)) 题型四:对数函数中的恒成立问题 题型五:对数函数的综合问题 【典例例题】题型一:对数运算及对数方程、对数不等式例1.(2022·全国·高三专题练习)(1)计算331log 2327lg 50lg 2+++; (2)已知()23log log lg 1x ⎡⎤=⎣⎦,求实数x 的值; (3)若185a =,18log 9b =,用a ,b ,表示36log 45. 【答案】(1)7;(2)109;(3)2a bb+-. 【解析】(1)利用对数恒等式和对数的运算法则计算即可; (2)利用指对互化可得实数x 的值;(3)先求出a ,再利用换底公式结合对数的运算法则求得结果.【详解】(1)原式=()23lg 510lg25lg51lg26lg5lg26lg107++⨯+=+++=++=+=;(2)因为()23log log lg 1x ⎡⎤=⎣⎦,所以()3log lg 2x =,所以2lg 39x ==,所以x =109;a 增大a 增大(3)因为185a =,所以18log 5a =,所以()()()181818183618181818log 59log 45log 5log 9log 45log 36log 182log 18log 189⨯+====⨯+÷1818181818log 5log 9log 18log 18log 92a bb++=+--.例2.(2022·全国·高三专题练习)(1)求23151log log 8log 2725⋅⋅的值. (2)已知9log 5=a ,37b =,试用a ,b 表示21log 35 【答案】(1)18;(2)21a bb ++. 【解析】 【分析】(1)首先根据题意得到原式()()()2352log 53log 23log 3=-⋅⋅-,再利用换底公式化简即可得到答案.(2)首先根据题意得到3log 7b =,3log 52=a ,再利用换底公式化简即可得到答案. 【详解】(1)原式()()()1233232355log 5log 2log 32log 53log 23log 3--=⋅⋅=-⋅⋅-lg5lg 2lg31818lg 2lg3lg5=⋅⋅⋅=(2)由37b =得到3log 7b =, 由9log 5=a ,得到31log 52=a ,即3log 52=a . 33321333log 35log 5log 72log 35log 21log 7log 31a bb ++===++.【点睛】本题主要考查对数的换底公式,同时考查指数、对数的互化公式,属于中档题.例3.(2022·全国·高三专题练习)(1)已知a ,b ,c 均为正数,且3a =4b =6c ,求证:212a b c+=;(2)若60a =3,60b =5,求12(1)12a bb ---的值. 【答案】(1)详见解析;(2)2. 【解析】【分析】(1)设3461a b c k ===>,应用指对数的互化有346log ,log ,log a k b k c k ===,进而应用换底公式及对数的运算性质分别求21a b +、2c,即可证结论;(2)应用指对数互化有6060log 3,log 5a b ==,应用对数的运算性质求12(1)a bb ---,进而可求12(1)12a b b ---的值.【详解】(1)设346a b c k ===,则1k >. ∴346log ,log ,log a k b k c k ===,∴3421212log 3log 4log 9log 4log 362log 6log log k k k k k k a b k k+=+=+=+==, 而6222log 6log k c k==, ∴212a b c+=. (2)由题设知:6060log 3,log 5a b ==,得606011log 5log 12b -=-=,60606011log 3log 5log 4a b --=--=, ∴60121260log 42log 21log 22(1)2log 122a b b --===-, 则121log 22(1)12122a b b ---==.例4.(2022·全国·模拟预测)若e 4a =,e 25b =,则( ) A .a +b =100 B .b -a =e C .28ln 2ab < D .ln6b a ->【答案】D 【解析】 【分析】利用指数和对数互化,得到a ,b 后逐项判断. 【详解】对于A ,由e 4a =,e 25b =,得ln 4a =,ln 25b =,所以ln 4ln 25ln100a b +=+=,故A 错误;对于B ,25ln 25ln 4ln4b a -=-=,故B 错误; 对于C ,2ln 4ln 252ln 2ln168ln 2ab =⨯>⨯=,故C 错误;对于D ,25ln 25ln 4lnln 64b a -=-=>,故D 正确. 故选:D .例5.(2022·全国·模拟预测)已知实数x ,y 满足0x >,0y >,1x ≠,1y ≠,y x x y =,log 4y xx y+=,则x y +=( ) A .2 B .4 C .6 D .8【答案】C 【解析】 【分析】 根据y x x y =得到lg lg x xy y =,再利用换底公式得到2x y=,利用lg 2lg x y =,即2x y =,求出4x =,2y =,所以6x y +=.【详解】由y x x y =,得lg lg y x x y =,lg lg x xy y=. 由log 4y x x y +=,lg log lg y x x y =,所以lg 4lg x x y y+=, 所以4x xy y +=,解得:2x y=,则lg 2lg x y =,即2x y =, 所以4x =,2y =,所以6x y +=, 故选:C.例6.(2022·北京昌平·二模)已知函数2()42(0)f x ax ax a =-+<,则关于x 的不等式2()log f x x >的解集是( )A .(,4)-∞B .(0,1)C .(0,4)D .(4,)+∞【答案】C 【解析】 【分析】由二次函数的性质判断()f x 区间单调性,根据解析式知()f x 恒过(4,2)且(0)2f =,进而确定区间值域,再由对数函数性质求2log y x =的对应区间值域,即可得不等式解集. 【详解】由题设,()f x 对称轴为2x =且图象开口向下,则()f x 在(0,2)上递增,(2,)+∞上递减, 由2()42(4)2f x ax ax ax x =-+=-+,即()f x 恒过(4,2)且(0)2f =, 所以(0,4)上()2f x >,(4,)+∞上()2f x ,而2log y x =在(0,)+∞上递增,且(0,4)上2y <,(4,)+∞上2y >,所以2()log f x x >的解集为(0,4). 故选:C例7.(2022·全国·江西师大附中模拟预测(文))已知函数()122log ,1,1,1,x x f x x x >⎧⎪=⎨⎪-≤⎩则不等式()(1)f x f x <-的解集为______.【答案】12x x ⎧⎫>⎨⎬⎩⎭【解析】 【分析】 分1x ≤、12x <≤和2x >,依次解不等式,再取并集即可.【详解】当1x ≤时,不等式()(1)f x f x <-为2211(1)x x -<--,解得112x <≤; 当12x <≤时,不等式()(1)f x f x <-为212log 1(1)x x <--,易知21122log log 10,1(1)0x x <=--≥,解得12x <≤;当2x >时,不等式()(1)f x f x <-为1122log log (1)x x <-,解得2x >;综上,解集为:12x x ⎧⎫>⎨⎬⎩⎭.故答案为:12x x ⎧⎫>⎨⎬⎩⎭.例8.(2022·辽宁·东北育才学校二模)若函数()f x 满足:(1)1x ∀,()20,x ∈+∞且12x x ≠,都有()()21210f x f x x x -<-;(2)()()1122x f f x f x x ⎛⎫=- ⎪⎝⎭,则()f x =___________.(写出满足这些条件的一个函数即可) 【答案】12log x,(log a x ,(0<a <1)都对)【解析】 【分析】满足第一个条件,表示函数是单调递减函数,第二个条件正好是符合对数的运算性质; 【详解】对于条件①,不妨设12x x <,则210x x ->,∵()()21210f x f x x x -<-,∴()()210f x f x -<∴12()()f x f x >,∴()f x 为()0,+∞上的单调递增函数,对于条件②,刚好符合对数的运算性质,故这样的函数可以是一个单调递减的对数函数. 故答案为:12log x.(log ax ,(0<a <1)都对)例9.(2022·全国·高三专题练习)设函数()log m f x x =(0m >且1m ≠)的图像经过点()3,1.(1)解关于x 的方程()()22(1)10f x m f x m +-+-=;(2)不等式()()10f x a f x +⋅->⎡⎤⎡⎤⎣⎦⎣⎦的解集是1,93⎛⎫⎪⎝⎭,试求实数a 的值. 【答案】(1)9x =或181x =;(2)2a =. 【解析】 【分析】(1)根据给定条件求出m 值,并代入方程,再解方程即得.(2)由给定解集借助对数函数单调性求出()f x 范围,换元借助一元二次不等式即可得解. 【详解】(1)由已知得()31f =,即log 31m =,则3m =,于是得()3log f x x =, 方程222()(1)()10()2()80f x m f x m f x f x +-+-=⇔+-=, 从而得()2f x =或()4f x =-,即3log 2x =或3log 4x =-,9x =或181x =, 所以原方程的根为9x =或181x =; (2)依题意,函数()3log f x x =中,1,93x ⎛⎫∈ ⎪⎝⎭,从而得()3log 1,2x ∈-.又()()()()3310log 1log 0f x a f x x x a +⋅->⇔+⋅-<⎡⎤⎡⎤⎣⎦⎣⎦,令3log x t =, 即一元二次不等式()()10t t a +⋅-<的解集为()1,2-,因此有-1,2是关于t 的方程()()10t t a +⋅-=的两根,则2a =, 所以实数a 的值为2.【方法技巧与总结】对数的有关运算问题要注意公式的顺用、逆用、变形用等.对数方程或对数不等式问题是要将其化为同底,利用对数单调性去掉对数符号,转化为不含对数的问题,但这里必须注意对数的真数为正.题型二:对数函数的图像例10.(2022·山东潍坊·二模)已知函数()()log a f x x b =-(0a >且1a ≠)的图像如图所示,则以下说法正确的是( )A .0a b +<B .1ab <-C .01b a <<D .log 0a b >【答案】C 【解析】 【分析】结合函数()f x 的图象可得1a >和10b -<<,然后逐项分析即可求出结果. 【详解】由图象可知()f x 在定义域内单调递增,所以1a >,令()()log 0a f x x b =-=,即1x b =+,所以函数()f x 的零点为1b +,结合函数图象可知011b <+<,所以10b -<<,因此0a b +>,故A 错误;0-<<a ab ,又因为1a >,所以1a -<-,因此1ab <-不一定成立,故B 错误;因为10b a a a -<<,即11b a a <<,且101a<<,所以01b a <<,故C 正确; 因为01b <<,所以log log 1a a b <,即log 0a b <,故D 错误, 故选:C.例11.(2022·江苏省高邮中学高三阶段练习)函数log (3)1(0a y x a =+->且1)a ≠的图象恒过定点A ,若点A 在直线10mx ny ++=上,其中0mn >,则11+m n的最小值为( ) A.3-B .1C . 3+D .2+【答案】C 【解析】 【分析】由对数函数的性质,可得()2,1A --,可得21m n +=,再根据基本不等式“1”的用法,即可求出结果.【详解】解:因为函数log (3)1(0a y x a =+->且1)a ≠的图象恒过定点()2,1A --,所以210m n --+=,即21m n +=, 所以()1111223n m m n m n m n m n⎛⎫+=++=++ ⎪⎝⎭, 又0mn >,所以0,0n mm n>>所以2333n m m n ++≥=,当且仅当2n m m n =,即1n =时取等号.故选:C.(多选题)例12.(2022·福建·莆田二中模拟预测)已知函数()()log a g x x k =+(0a >且1a ≠)的图象如下所示.函数()()1x xf x k a a -=--的图象上有两个不同的点()11,A x y ,()22,B x y ,则( )A .1a >,2k >B .()f x 在R 上是奇函数C .()f x 在R 上是单调递增函数D .当0x ≥时,()()22f x f x ≤【答案】BCD 【解析】 【分析】对于A 结合对数型函数图像相关知识求解;对于B 运用定义法判断()f x 是否在R 上是奇函数;对于C 运用定义法判断函数单调性;对于D 通过作差法并对式子变形即可判断. 【详解】对于A ,由图像可知,函数()()log a g x x k =+(0a >且1a ≠)在()2,-+∞上单调递增,所以1a >,因为()g x 经过()1,0-,所以()()1log 10a g k -=-+=,所以01a k =-+,2k =,故A 错误.对于B ,()x x f x a a -=-,定义域R 关于原点对称,()()x xf x a a f x --=-=-,所以()f x 在R 上是奇函数,故B 正确.对于C ,对于()x xf x a a -=-,由题意不妨令1212,,x x x R x R >∈∈,则()()()()()121212121212121212111x x x x x x x x x x x x x x x x a a a a a f x f x a a a a a a a a ++++--⎛⎫⎛⎫-=---=-+=⎪ ⎪⎝⎭⎝⎭,因为1212,,x x x R x R >∈∈,1a >,所以12121210,0,0x x x x x x a a a a +++>>->,即()()12f x f x >,所以()f x 在R 上是单调递增函数,故C 正确.对于D ,()()()()()()()()()2222222x x x x x x x x x x x x x x a a a a a a a a a a a a a x f a f x --------=---=---+--=-()()()()22322221111112x x x x x x xx xxxa a a a a a a a a aa----+-⎛⎫⎛⎫--=⎪-==⎪⎝⎭⎝⎭,因为1a >,0x ≥,所以()3210,010,xxxa a a +≥>->,所以()()23101x x xa a a-+-≤,当且仅当0x =时等号成立,即当0x ≥时,()()22f x f x ≤成立,故D 正确.故选:BCD例13.(2022·全国·高三专题练习)已知223,20(){1ln ,021x x x f x x x -+-≤<=≤≤+,若()()g x f x ax a =--的图象与x 轴有3个不同的交点,则实数a 的取值范围为______. 【答案】ln 31[,)3e【解析】 【分析】由分段函数解析式,结合导数研究|()|f x 的性质,再将问题转化为|()|f x 与(1)y a x =+有3个不同交点,应用数形结合的思想有(1)y a x =+与|()|f x 在02x ≤≤上至少有2个交点,最后由导数求它们相切或(1)y a x =+过(2,ln 3)时参数a 的值,即可知a 的取值范围. 【详解】由题设,20x -≤<上239()2()48f x x =--+,故值域为[14,0]-且单调递增;02x ≤≤上()f x '=101x -<+,故()f x 值域为[ln 3,0]-且单调递减; ∴|()|f x 在20x -≤<上值域为[0,14]且单调递减;在02x ≤≤上值域为[0,ln 3]且单调递增; 要使()g x 与x 轴有3个不同的交点,即|()|f x 与(1)y a x =+有3个不同交点,它们的图象如下:∴由图知:要使函数图象有3个交点,则(1)y a x =+与|()|f x 在02x ≤≤上至少有2个交点, 由02x ≤≤,1()|()|ln1g x f x x ==-+,则1()|()|1g x f x x '==+,此时,若|()|f x 与(1)y a x =+相切时,切点为(,(1))m a m +, ∴111ln (1)1a m a m m ⎧=⎪⎪+⎨⎪-=+⎪+⎩,可得1e a =,当(1)y a x =+过(2,ln 3)时,有3ln3a =,得ln 33a =, ∴ln 313ea ≤<. 故答案为:ln 31[,)3e【点睛】关键点点睛:根据已知研究|()|f x 的性质,并将问题转化为|()|f x 与(1)y a x =+的交点问题,应用导数的几何意义、数形结合的思想求参数范围.【方法技巧与总结】研究和讨论题中所涉及的函数图像是解决有关函数问题最重要的思路和方法.图像问题是数和形结合的护体解释.它为研究函数问题提供了思维方向.题型三:对数函数的性质(单调性、最值(值域))例14.(2022·陕西·榆林市第十中学高二期中(文))函数()22log 43y x x =+-的一个单调增区间是( ) A .3,2⎛⎫-∞ ⎪⎝⎭B .3,2∞⎡⎫+⎪⎢⎣⎭C .31,2⎛⎫- ⎪⎝⎭D .3,42⎡⎫⎪⎢⎣⎭【答案】C 【解析】【分析】先求出函数的定义域,再利用复合函数单调性法则“同增异减”即可求解.【详解】函数()22log 43y x x=+-的定义域为()1,4-.要求函数()22log 43y x x =+-的一个单调增区间,只需求243y x x =+-的增区间,只需32x <. 所以312x -<<. 所以函数()22log 43y x x =+-的一个单调增区间是31,2⎛⎫- ⎪⎝⎭. 故选:C例15.(2022·天津·南开中学二模)已知函数()21,14log 1,1a ax x x f x x x ⎧--≤⎪=⎨⎪->⎩是R 上的单调函数,则实数a 的取值范围为( ) A .11,42⎡⎫⎪⎢⎣⎭B .11,42⎡⎤⎢⎥⎣⎦C .10,2⎛⎤ ⎥⎝⎦D .1,12⎛⎫ ⎪⎝⎭【答案】B 【解析】 【分析】分函数()f x 在R 上的单调递减和单调递增求解. 【详解】当函数()21,14log 1,1a ax x x f x x x ⎧--≤⎪=⎨⎪->⎩是R 上的单调递减函数,所以01112514a aa ⎧⎪<<⎪⎪≥⎨⎪⎪-≥-⎪⎩,解得1142a ≤≤,因为0a >且1a ≠,所以当1x ≤时,()f x 不可能是增函数,所以函数()f x 在R 上不可能是增函数,综上:实数a 的取值范围为11,42⎡⎤⎢⎥⎣⎦,故选:B例16.(2022·浙江·模拟预测)己知实数,(1,)∈+∞a b ,且33log log 3log log 4b a a b +=+,则( ) Ab a << B.b a < Ca b < D.a b <<【答案】A 【解析】 【分析】对33log log 4log log 3a b a b -=-利用换底公式等价变形,得333311log log log log -<-b a b a,结合1y x x=-的单调性判断b a <,同理利用换底公式得343411log log log log b a b a ->-,即34log log b a >,再根据对数运算性质得4log log log a =>3log y x =单调性,b >解. 【详解】由33log log 4log log 3a b a b -=-可得333343111log log log log log log b a a b a a-=-<-, 因为1y x x=-在(,0),(0,)-∞+∞上单调递增,且3log a ,3log (0,)b ∈+∞,所以33log log b a <,即b a <, 其次,343411log log log log b a b a->-,所以34log log b a >,又因为4log log log a =>3log y x =单调递增,所以由3log log b >b >b a <. 故选:A例17.(2022·全国·高三专题练习(理))函数f (x )=log ax (0<a <1)在[a 2,a ]上的最大值是( ) A .0 B .1 C .2 D .a【答案】C 【解析】【分析】根据对数函数的单调性可求出结果. 【详解】∵0<a <1,∴f (x )=log ax 在[a 2,a ]上是减函数, ∴f (x )max =f (a 2)=log aa 2=2. 故选:C例18.(2022·重庆·模拟预测)若函数()2()log 341a f x x ax =-+-有最小值,则实数a 的取值范围是( )A .⎫⎪⎪⎝⎭B .C .⎛ ⎝⎭D .)+∞【答案】A 【解析】 【分析】根据对数函数的性质可得()()0,11,a ∈+∞且23410x ax -+->,则0∆>,即可求出a 的大致范围,再令23410x ax -+-=的根为1x 、2x 且12x x <,()2341u x x ax =-+-,log a y u =,对a 分两种情况讨论,结合二次函数、对数函数的单调性判断即可; 【详解】解:依题意()()0,11,a ∈+∞且23410x ax -+->,所以216120a ∆=->,解得a >a <()1,a ⎫∈+∞⎪⎪⎝⎭,令23410x ax -+-=的根为1x 、2x 且12x x <,()2341u x x ax =-+-,log a y u =,若()1,a ∈+∞,则log a y u =在定义域上单调递增,()2341u x x ax =-+-在12,3a x ⎛⎫ ⎪⎝⎭上单调递增,在22,3a x ⎛⎫⎪⎝⎭上单调递减,根据复合函数的单调性可知,()2()log 341a f x x ax =-+-在12,3a x ⎛⎫ ⎪⎝⎭上单调递增,在22,3a x ⎛⎫ ⎪⎝⎭上单调递减,函数不存在最小值,故舍去;若a ⎫∈⎪⎪⎝⎭,则log a y u =在定义域上单调递减,()2341u x x ax =-+-在12,3a x ⎛⎫⎪⎝⎭上单调递增,在22,3a x ⎛⎫ ⎪⎝⎭上单调递减,根据复合函数的单调性可知,()2()log 341a f x x ax =-+-在12,3a x ⎛⎫⎪⎝⎭上单调递减,在22,3a x ⎛⎫ ⎪⎝⎭上单调递增,所以函数在23a x =取得最小值,所以a ⎫∈⎪⎪⎝⎭; 故选:A【方法技巧与总结】研究和讨论题中所涉及的函数性质是解决有关函数问题最重要的思路和方法.性质问题是数和形结合的护体解释.它为研究函数问题提供了思维方向.题型四:对数函数中的恒成立问题例19.(2022·北京·高三专题练习)若不等式2log 0a x x -<在10,2⎛⎫ ⎪⎝⎭内恒成立,则a 的取值范围是( ) A .1116a ≤< B .1116a << C .1016a <≤D .1016a <<【答案】A 【解析】 【分析】根据对数函数的图象与性质,分1a >和01a <<两种情况分类讨论,结合函数的单调性,列出不等式,即可求解. 【详解】当1a >时,由1(0,)2x ∈,可得log 0a x <,则log 0a x ->,又由20x >,此时不等式2log 0a x x -<不成立,不合题意;当01a <<时,函数log a y x =在1(0,)2上单调递减,此时函数log a y x =-在1(0,)2上单调递增,又由2yx 在1(0,)2上单调递增,要使得不等式2log 0a x x -<在1(0,)2内恒成立,可得211()log 022a -≤,解得1116a ≤<.故选:A.例20.(2022·江苏·高三专题练习)已知函数22414ax x y -+⎛⎫= ⎪⎝⎭的值域为10,16⎛⎤⎥⎝⎦,若不等式()()log 4log 2x a x a t t ⋅<-在[]1,2x ∈上恒成立,则t 的取值范围是( ) A .2,25⎛⎫ ⎪⎝⎭B .2,5⎛⎫+∞ ⎪⎝⎭C .(,2)-∞D .()0,2【答案】A 【解析】根据题意,先求得12a =,把不等式()()1122log 4log 2x x t t ⋅<-在[]1,2x ∈上恒成立,转化为402042x xx x t t t t ⎧⋅>⎪->⎨⎪⋅>-⎩在[]1,2x ∈上恒成立,结合指数幂的运算性质,即可求解. 【详解】由题意,函数22414ax x y -+⎛⎫= ⎪⎝⎭的值域为10,16⎛⎤⎥⎝⎦,可得函数y 的最大值为116,当0a =时,函数2414x y -+⎛⎫= ⎪⎝⎭显然不存在最大值;当0a >时,函数22414ax x y -+⎛⎫= ⎪⎝⎭在1,x a ⎛⎫∈-∞ ⎪⎝⎭上单调递增,在1,x a ⎛⎫∈+∞ ⎪⎝⎭上单调递减,当1x a =时,函数y 有最大值,即12411416a a -+⎛⎫= ⎪⎝⎭,解得12a =; 当0a <时,22414ax x y -+⎛⎫= ⎪⎝⎭在1,x a ⎛⎫∈-∞ ⎪⎝⎭上单调递减,在1,x a ⎛⎫∈+∞ ⎪⎝⎭上单调递增,此时函数y 无最大值,所以()()1122log 4log 2x xt t ⋅<-在[]1,2x ∈上恒成立, 即402042x xx x t t t t ⎧⋅>⎪->⎨⎪⋅>-⎩在[]1,2x ∈上恒成立, 由40x t ⋅>在[]1,2x ∈上恒成立,可得0t >;由20x t ->在[]1,2x ∈上恒成立,即2x t <在[]1,2上恒成立,可得2t <; 由42x x t t ⋅>-在[]1,2x ∈上恒成立,即2114122x x x xt >=++在[]1,2上恒成立,令()122xxf x =+,可得函数()f x 在[]1,2上单调递增,所以()()min512f x f ==,即25t >, 综上可得225t <<,即实数t 的取值范围是2,25⎛⎫⎪⎝⎭.故选:A. 例21.(2022·浙江·高三阶段练习)已知函数()29x f x x+=,()2log g x x a =+,若存在[]13,4x ∈,任意[]24,8x ∈,使得()()12f x g x ≥,则实数a 的取值范围是___________. 【答案】13,4∞⎛⎤- ⎥⎝⎦【解析】 【分析】将问题转化为在对应区间上max max ()()f x g x ≥,结合对勾函数、对数函数的性质求()f x 、()g x 的区间最值,即可求a 的范围. 【详解】若()f x 在[3,4]上的最大值max ()f x ,()g x 在[4,8]上的最大值max ()g x , 由题设,只需max max ()()f x g x ≥即可.在[3,4]上,9()6f x x x =+≥=当且仅当3x =时等号成立, 由对勾函数的性质:()f x 在[3,4]上递增,故max 25()4f x =. 在[4,8]上,()g x 单调递增,则max ()3g x a =+, 所以2534a ≥+,可得134a ≤.故答案为:13,4∞⎛⎤- ⎥⎝⎦.例22.(2022·全国·高三专题练习)已知函数()ln f x x x =-,已知实数0a >,若2()e ln 0x f x a a ++≥在()0+∞,上恒成立,求实数a 的取值范围. 【答案】12ea ≥. 【解析】 【分析】把不等式作等价变形,构造函数()ln g x x x =+,借助其单调性可得2e x a x ≥,分离参数构造函数并求出最大值作答. 【详解】函数()ln f x x x =-定义域为(0,)+∞,则(0,)∀∈+∞x :222()e ln 0e ln l 2n e ln ln x x x f x a a a a x a a x x x x++≥⇔+≥⇔+≥+++22e e )n ln(l x x a a x x ⇔≥++,令()ln g x x x =+,函数()g x 在(0,)+∞上单调递增,则有原不等式等价于()()2e xg a g x ≥22e e x xx a x a ⇔≥⇔≥, 令2()e x x h x =,0x >,求导得:212()exx h x -'=,当102x <<时,()0h x '>,当12x >时,()0h x '<, 因此,函数()h x 在1(0,)2上单调递增,在1(,)2+∞上单调递减,当12x =时,max 11()()22eh x h ==,则12ea ≥, 所以实数a 的取值范围是12ea ≥. 【点睛】关键点睛:涉及不等式恒成立问题,将给定不等式等价转化,借助同构思想构造函数,利用导数探求函数单调性、最值是解决问题的关键.例23.(2022·全国·高三专题练习)已知函数()log (0,1)xa f x a x a a =+>≠在[1,2]上的最大值与最小值之和为6log 2a +. (1)求实数a 的值;(2)对于任意的[2,)x ∈+∞,不等式()10kf x -≥恒成立,求实数k 的取值范围. 【答案】(1)2;(2)1,5⎡⎫+∞⎪⎢⎣⎭【解析】 【分析】(1)根据指对数函数的单调性得函数()log (0,1)xa f x a x a a =+>≠在[1,2]上是单调函数,进而得260+-=a a ,解方程得2a =;(2)根据题意,将问题转化为对于任意的[2,)x ∈+∞,1()k f x ≥恒成立,进而求函数的最值即可. 【详解】解:(1)因为函数,log (0,1)xa y a y x a a ==>≠在[1,2]上的单调性相同, 所以函数()log (0,1)xa f x a x a a =+>≠在[1,2]上是单调函数,所以函数()f x 在[1,2]上的最大值与最小值之和为2log 26log 2a a a a ++=+,所以260+-=a a ,解得2a =和3a =-(舍) 所以实数a 的值为2.(2)由(1)得2()2log x f x x =+,因为对于任意的[2,)x ∈+∞,不等式()10kf x -≥恒成立,所以对于任意的[2,)x ∈+∞,1()k f x ≥恒成立, 当[2,)x ∈+∞时,2()2log x f x x =+为单调递增函数, 所以()()25f x f ≥=,所以11()5f x ≤,即15k ≥ 所以实数k 的取值范围1,5⎡⎫+∞⎪⎢⎣⎭【点睛】本题考查指对数函数的性质,不等式恒成立求参数范围,考查运算求解能力,回归转化思想,是中档题.本题第二问解题的关键在于根据题意,将问题转化为任意的[2,)x ∈+∞,1()k f x ≥恒成立求解.例24.(2022·陕西安康·高三期末(文))已知函数()()()2log 2log 30,1a a f x x x a a =++>≠. (1)若()32f =,求a 的值;(2)若对任意的[]8,12x ∈,()6f x >恒成立,求a 的取值范围.【答案】(1)13a =;(2)()1,11,82⎛⎫⋃ ⎪⎝⎭. 【解析】 【分析】(1)由()32f =可求得log 3a 的值,进而可求得实数a 的值;(2)由()6f x >可得出log 3a x <-或log 1>a x ,分01a <<、1a >两种情况讨论,可得出关于实数a 的不等式,由此可解得实数a 的取值范围. (1)解:因为()32f =,所以()2log 32log 332a a ++=,所以()2log 310a +=,所以log 31a =-,解得13a =.(2)解:由()6f x >,得()2log 2log 30a a x x +->,即()()log 3log 10a a x x +->,即log 3a x <-或log 1>a x .当01a <<时,log 12log log 8a a a x ≤≤,则log 83a <-或log 121a >,因为log 12log 10a a <=,则log 121a >不成立,由log 83a <-可得318a ⎛⎫< ⎪⎝⎭,得112a <<;当1a >时,log 8log log 12a a a x ≤≤,则log 123a <-或log 81a >,因为log 12log 10a a >=,则log 123a <-不成立,所以log 81a >,解得18a <<. 综上,a 的取值范围是()1,11,82⎛⎫⋃ ⎪⎝⎭.例25.(2022·上海·高三专题练习)已知2()32log f x x =-,2()log g x x =. (1)当[]1,4x ∈时,求函数[]()1()y f x g x =+⋅的值域;。
高考数学压轴题100题汇总(含答案)

高考数学压轴题100题汇总(含答案)1. 设函数f(x) = x^3 3x + 1,求f(x)的极值点和极值。
答案:f(x)的极值点为x = 1和x = 1,极值分别为f(1) = 1和f(1) = 3。
2. 已知等差数列{an}的前n项和为Sn = n^2 + n,求该数列的通项公式。
答案:an = 2n + 1。
3. 已知三角形ABC中,AB = AC = 5,BC = 8,求三角形ABC的面积。
答案:三角形ABC的面积为12。
4. 设直线y = kx + b与圆x^2 + y^2 = 1相切,求k和b的值。
答案:k = ±√3/3,b = ±√6/3。
5. 已知函数f(x) = log2(x^2 + 1),求f(x)的导数。
答案:f'(x) = 2x/(x^2 + 1)ln2。
6. 已知向量a = (2, 3),向量b = (1, 4),求向量a和向量b的夹角。
答案:向量a和向量b的夹角为arccos(1/√5)。
7. 已知矩阵A = [1 2; 3 4],求矩阵A的逆矩阵。
答案:矩阵A的逆矩阵为[4 2; 3 1]。
8. 已知函数f(x) = x^3 6x^2 + 9x + 1,求f(x)的零点。
答案:f(x)的零点为x = 1和x = 3。
9. 已知函数f(x) = sin(x) cos(x),求f(x)在区间[0, π/2]上的最大值。
答案:f(x)在区间[0, π/2]上的最大值为√2。
10. 已知函数f(x) = x^2 + 4x + 4,求f(x)的顶点坐标。
答案:f(x)的顶点坐标为(2, 0)。
高考数学压轴题100题汇总(含答案)11. 已知函数f(x) = e^x 2x,求f(x)的导数。
答案:f'(x) = e^x 2。
12. 已知函数f(x) = x^2 4x + 4,求f(x)的极值点和极值。
答案:f(x)的极值点为x = 2,极值为f(2) = 0。
