三垂线定理及其应用
立体几何:三垂线定理及其简单应用

立体几何:三垂线定理及其简单应用新课标高中数学中,淡化了“三垂线定理及逆定理”,但我们认为:三垂线定理还是非常好用的。
至少用它来证明有关题目,会简捷得多!(一)温故知新,引入课题大家已经学习了直线和平面的垂直关系,学新课之前,让我们作个简单的回顾:1.直线和平面垂直的定义?2.直线和平面垂直的判定定理?(二)猜想推测,激发兴趣(三)层层推进,证明定理我们在讨论立体空间时,通常会想把空间的问题转化为平面问题,那有没有什么方法可以帮助我们将空间与平面联系在一起呢? · 今天我们学习的内容,就可以把空间垂直的问题转化为平面垂直的问题。
这就是:三垂线定理与三垂线逆定理 .我们先来看一下三垂线定理及逆定理的描述。
1、三垂线定理:平面内的一条直线,如果和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
2、三垂线定理的逆定理:如果平面内一条直线和该平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
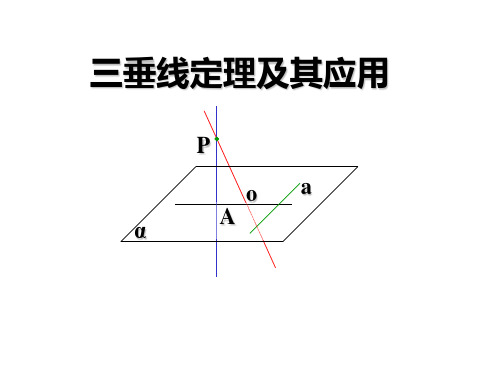
具体在图中体现为:我们将OP称为平面的斜线,PA是平面的垂线,AO是OP在平面内的射影,a是平面内的一条直线,若a与AO 垂直,则l也与PO垂直,反之亦然。
其实三垂线定理从证明的角度看可以认为是线面垂直转化关系的一个常用推论.这是一个标准的从线线垂直(一般是共面)转化为线面垂直又转化为新的线线垂直(一般是异面)的立体几何推理过程。
但换一个观点和角度来看,三垂线定理的价值在于将一个需要进行多次转化而且模式基本确定的证明过程以定理的形式规范下来,这使得在相关的证明(之后还有计算)过程中书写难度得到有效降低,在部分复杂题目中更是如此。
而从很多立体几何题目设计的思路来看,经常会出现两条看似无关直线(一般是异面)的关系问题,一般方法是让他们在不同平面中分别找关系,然后利用一个桥梁进行沟通;三垂线定理正是提供了这样一个可以进行简便沟通的方式。
而更为重要的是,在三垂线定理中,最重要的其实并不是斜线或者射影(尽管它们分别是条件和结论),而是平面的垂线!有了这个垂线的存在,才会使得两条异面直线建立关系;有了这个垂线,才能形成相应的平面和直角三角形从而便于计算;而同样也是因为有了这条垂线,使得直线和平面所称的角,以及升级版的平面和平面所成的角(二面角)出现并有了用平面角度量其大小的方式。
高三数学三垂线定理及其运用

B
b
9、已知斜三棱柱ABC-A1B1C1的各棱长均为2;侧棱与底面所成的角为 ,且侧面ABB1A1垂直于底面;判定B1C与C1A是否垂直;并证明你的结论。
C1
B1A1
C
B A
6、如图;E,F分别为正方体的面ADD1A1、面BCC1B1中心;则四边形BFD1E在该正方体的面上的射影可能是2,3。(要求:把可能的图的序号都填上)
D1C1
A1B1
E
F
D C (1) (2) (3) (4)
A BA
7、如图;已知三棱锥A-BCD中;AB⊥CD,AC⊥BD,
求证;AD⊥BC
D
B
C
8、已知AB是异面直线a、b的公垂到直线b的距离。
二、知能达标
1、如图:AB是圆的直径;C是圆周上一点;PC垂直圆所在平面;若BC=1,AC=2,则P到直线AB的距离为( D )
A . 1 B.2C. D. P
2.、PA、PB、PC是从P点引出的三条射线;它们每两条的夹角都是60°C
则直线PC与平面PAB所成的角是( C )AB
A 45°B60°C arccos D arctg
2如果直线a与平面 内的一条直线b平行;那么a∥ 。A B
3 如果直线a与平面 内的两条直线b、c都垂直;那么 。A
4如果平面 内的一条直线a垂直平面 ;那么 。
5、如图;∠BAD=90°的等腰直角三角形ABD与正三角形CBDB D
所在的平面互相垂直;E是BC的中点;则AE与平面BCD所成的E
角的大小45°。C
3、三棱柱ABC-A1B1C1,侧棱BB1在下底面上射影平行AC;如果侧棱BB1与底面所成的角为30°;∠B1BC=60°;则∠ACB的余弦为(A)C1
三垂线定理知识点总结

三垂线定理知识点总结一、三垂线定理的定义三垂线定理是指在一个三角形中,三条垂线经过一个顶点交于同一点。
具体来说,如果在一个三角形中,我们分别从三个顶点做垂线,那么这三条垂线会相交于同一个点,这个点就叫做三角形的垂心。
垂心是三角形内心的一种特殊情况,也是三角形的一个重要点。
二、三垂线定理的性质1. 三角形的垂心是三角形内心的一种特殊情况。
2. 三角形的垂心到三条边的距离相等。
3. 垂心到三角形三个顶点的连线叫做垂径,垂心到垂径的距离相等。
4. 垂心到三角形三个顶点的连线叫做垂线,垂心到垂线的距离最小。
5. 三角形的三个垂线相交于同一个点。
三、三垂线定理的证明三垂线定理的证明需要借助一些平面几何的知识和方法。
一般来说,我们可以采用反证法来证明三垂线定理,具体步骤如下:1. 假设垂心不是三个垂线的交点,即存在一个点不受三个垂线的影响。
2. 利用垂线的定义和性质,通过绘制辅助线和辅助角等方法,得出矛盾结论。
3. 由矛盾推出假设错误,即证明垂心是三个垂线的交点。
三垂线定理的证明比较复杂,需要结合具体的题目和图形进行推敲,但掌握了相关的证明方法后,就可以轻松应对各种类型的证明题目。
四、三垂线定理的应用三垂线定理在解题中有着广泛的应用,特别是在证明题和计算题中。
下面通过几个例题的分析,来展示三垂线定理的应用。
例1:如图,在△ABC中,AD ⊥ BC,BE ⊥ AC,CF ⊥ AB,垂足分别为D,E,F,连接AD,BE,CF相交于H。
证明:H是△ABC的垂心。
解:根据题意可知,H是由AD,BE,CF三个垂线相交而成的交点,而AD,BE,CF分别是△ABC三条边的垂线,所以H是△ABC的垂心。
例2:如图,点P是△ABC内部一点,PA,PB,PC分别交△ABC的边BC,CA,AB于D,E,F。
证明:若P为△ABC的垂心,则△DEF的三条边和面积与△ABC的相似。
解:首先我们可以利用三垂线定理来证明P是△ABC的垂心,然后我们可以利用相似三角形的性质来证明△DEF与△ABC的相似性。
【数学课件】三垂线定理

E
二、应用
例1.已知学校的旗杆高20米,测量得旗杆底部B到楼底 部的距离为8米,求旗杆顶部A到楼底部的距离。
A 解:过B作楼底部所在直线 EF 的垂线BC 垂足为C,
F
C
B
E
二、应用
例1.已知学校的旗杆高20米,测量得旗杆底部B到楼底 部的距离为8米,求旗杆顶部A到楼底部的距离。
A 解:过B作楼底部所在直线 EF 的垂线BC 垂足为C,
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米,测量得旗杆底部B到楼底 部的距离为8米,求旗杆顶部A到楼底部的距离。
A 解:过B作楼底部所在直线 EF 的垂线BC 垂足为C,
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米,测量得旗杆底部B到楼底 部的距离为8米,求旗杆顶部A到楼底部的距离。
证明:∵AC面,a 面
∴ACa
一、三垂线定理
1.三垂线定理:在平面内的一条直线,如果和这个平面的一条 A 斜线的射影垂直,那么它也和这条斜线垂直。
已知:AC和AB分别是平面的垂
线和斜线,BC是AB在平面
C
B
a
上的射影,a,aBC。 求证: aAB。
证明:∵AC面,a 面
∴ACa
∵BCa ,AC∩BC=C
9.4 直线与平面垂直的判定和性质
————————————————————— —
§6 三垂线定理
教学目的
• 掌握三垂线定理及逆定理 • 运用三垂线定理及逆定理解决数学问题 • 在实际生活中运用三垂线定理及逆定理
重点与难点
•三垂线定理及逆定理的适用条件 •三垂线定理及逆定理的应用
浅析教学三垂线定理的实际应用

二
咨
旗 }
数
・ 堂 t 。 工
解: 在道路边取一点 c , 使B C与道边所成水平 角等于 9 O “ . ‘ B C是 A C的射 影 , 且C D上B C, . . . C D上 c ( 三 垂 线 定理 ) , 因此 斜
( 一) 三垂线定理及其逆定理所论述的三个垂直关系以及所 涉及的一个平面, 即“ 一面四线” { 其次掌握运用定理的五个步骤:
其关 键是 确定平 面 的垂线 。
我们在第一点中谈到从表面到内部, 制图中的投影方法是正 爹 我们看到的真实的形状, 且表面方法主要是在三方面进行 娄 § 确定 平面 作 出垂 线 ; 找到斜线; 确 定射 影 ; 得 出 所证 的垂 直 关 系。 投影,
的一个重要定理。它既是线面垂直关系的一个应用, 又为以后学习面面垂直, 研究空阃距离、 空间角、 多面体与旋转体的性质奠定了基础。
关键 词 : 垂线 ; 空间 ; 三垂线 定理 中图分类号 : G 6 3 3
一
文献 标识码 : A
文 章编号 : 1 0 0 5— 6 3 5 1 ( 2 0 1 3 ) 一 0 2 — 0 1 4 1 — 0 2
一般情况下为前后、 左右、 上下。 这主要 理 和性质定 理 。要注 意从 图中找 线线 垂 直 ( 可 充分 利用 立 体图 形 是三个方向的观察顺序,
的概 念 , 平 面 图形 的性质 ) 或通 过适 当作 辅助 线产 生线 线垂 直 , 目 的接受各个表面的结构形状, 然后把三个方向的结构统一的结合 的是为运用三垂线定理及其逆定理创造条件。 起来 , 在 我们 的脑子 中间 形成 了一 个 完整 的型 体 , 并把 其 主 要 的 例l 、 如图 1 , 道路旁有一 条河 , 彼岸有电塔 A B, 高1 5 m, 只有 测角 器和皮 尺作 测量工 具 , 不 过河 能否 求 出 电塔 顶 A与道 路 的距 离? ( 测 角器 只能测 水平 面角 ) ( 三) 针 对型 体的结 构进 行 分类 , 主要 有 切 割 、 叠加 及杂 合三
三垂线定理及其应用
∵底面ABCD是正方形,∴AC⊥BD, A1 而E,F为AB和AD中点, ∴EF∥BD, ∴ EF⊥AC
又因为AG为A1G在平面ABCD F 上的射影.(由三垂线定理) ∴ EF⊥A1G,则∠A1GA为二面角的平 A 面角. 计算得:二面角的大小为:60o
D B1
C1
C
G E B
练习:
3.如图.在一个45o的Байду номын сангаас面角的一个平面α内有一条 直线PA与二面角棱成45o,则此直线与二面角的另 一个平面β所成角为______. 30o
练习:
1. 如图,PA垂直⊙O所在平面,AB为圆的直径,C 为 圆上 的任意一点(不同于A,B),则图中有多少个直角三角形?
P
答:有4个,分别是: △PAB,△PAC,△ACB,△PCB. A
O
B
C
三垂线定理 定理应用 例3,道路旁有一条河,彼岸有电塔AB,高15m,只有测角 器和皮尺作测量工具,不过河能否求出电塔顶A与道路的 距离?(测角器只能测水平面角)
三垂线定理及其应用
P A o
a
α
三线概念: 平面的斜线、垂线、射影
三垂线定理
PO是平面α的斜线,
P
A
O为斜足; PA是平面α 的垂线, A为垂足; AO
o
a
是PO在平面α内的射 影.
α
三垂线定理:在平面内的一条直线(a),如果和这个平面 的一条斜线(PO)的射影(AO)垂直,那么它(a)也和这条斜线垂直。
三垂线定理及证明

三垂线定理及证明三垂线定理是几何学中的重要定理之一。
它指出,在一个三角形中,从顶点向对边作垂线,这些垂线的交点将会共线。
这一定理的证明可以通过几何推理来完成。
我们来考虑一个任意的三角形ABC。
我们从顶点A向边BC作垂线AD,从顶点B向边AC作垂线BE,从顶点C向边AB作垂线CF。
我们的目标是证明这三条垂线所在的线段DF是共线的。
为了证明这一点,我们需要使用一些基本的几何定理和性质。
首先,我们知道在一个直角三角形中,垂线会相交于直角顶点。
所以,我们可以得出结论,AD与BC相交于点D,BE与AC相交于点E,CF与AB相交于点F。
接下来,我们需要证明点D、E、F三者共线。
我们可以通过反证法来进行证明。
假设点D、E、F不共线,即它们不在同一条直线上。
那么我们可以得出结论,线段DE与线段DF不平行,且线段EF与线段DF不平行。
现在我们来考虑三个小三角形,即三角形ADE、三角形BEF和三角形CDF。
由于线段DE与线段DF不平行,根据平行线性质可知,∠DAE与∠DFA不等。
同理,根据线段EF与线段DF不平行,可知∠FEB与∠FDB不等。
从而我们可以得到结论,∠DAE + ∠FEB + ∠FDB ≠ 180°,这与三角形内角和定理相矛盾。
因此,我们可以推断出点D、E、F必须共线。
这就证明了三垂线定理。
三垂线定理在几何学中有着广泛的应用。
首先,在解决三角形相关问题时,我们可以利用三垂线定理来推导出一些有用的结论。
例如,通过三垂线定理,我们可以证明三角形的垂心存在,即三条垂线的交点。
垂心在三角形的性质研究中有着重要的地位。
三垂线定理也可以用于解决一些几何问题。
例如,在解决平面几何问题时,我们可以利用三垂线定理来推导出一些几何关系,从而简化问题的解决过程。
总结起来,三垂线定理是几何学中的重要定理之一。
它指出,在一个三角形中,从顶点向对边作垂线,这些垂线的交点将会共线。
这一定理可以通过几何推理来证明,其证明过程中运用了一些基本的几何定理和性质。
三垂线定理及其逆定理三垂线定理的应用三垂线法求二面角

三垂线定理及其逆定理•正射影的概念:自一点向平面引垂线,垂足叫做这一点在平面内的正射影(简称为射影);平面的斜线的概念:如果一条直线和一个平面相交但不垂直,那么这条直线叫做这个平面的斜线,斜线和平面的交点叫做斜足。
•三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:如果平面内一条直线和穿过该平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
•三垂线定理与其逆定理的关系:即:•三垂线定定理的主要应用:证明线线、线面垂直,求点到线的距离、二面角大小。
应用两个定理解题的一般思路:平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:如果平面内一条直线和穿过该平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
证明:1)用线面垂直证明已知:如图,PO在α上的射影OA垂直于a三垂线定理的证明三垂线定理的证明求证:OP⊥a证明:过P做PA垂直于α∵PA⊥α且a⊆α∴a⊥PA又a⊥OAOA∩PA=A∴a⊥平面POA∴a⊥OP(2)用向量证明三垂线定理1.已知:PO,PA分别是平面α的垂线,斜线,OA是PA在α内的射影,向量b包含于α,且向量b垂直于OA,求证:向量b垂直于PA证明:∵PO垂直于α,∴PO垂直于b,又∵OA垂直b,向量PA=(向量PO+向量OA)∴向量PA·向量b=(向量PO+向量OA)·向量b=(向量PO·向量b)+(向量OA·向量b )=0,∴PA⊥向量b。
2.已知三个平面OAB,OBC,OAC相交于一点O,∠AOB=∠BOC=∠COA=60度,求交线OA与平面OBC所成的角。
解:∵向量OA=(向量OB+向量AB),O是内心,又∵AB=BC=CA,∴OA与平面OBC所成的角是30°。
用途在做图中,做二面角的平面角在证明中,证明线线垂直在计算中,用归纳法归拢已知条件,便于计算口诀线射垂,线斜垂;线斜垂,线射垂。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
C
A
B
同理:BA1是斜线BD1在平面ABB1A1上的射影 , AB1 ⊥ BD1 而AC ∩AB1 =A ∴BD1⊥平面AB1C
例3.道路旁有一条河,彼岸有电塔AB,高15m,只有测角 器和皮尺作测量工具,不过河能否求出电塔顶A与道路的 距离?(测角器只能测水平面角) 解:在道路边取一点C,使BC与道边所成水平角等于90°,
且b垂直于a在β内的射影,则a⊥b。
( ×)
强调:1°四线是对同一个平面而言.
2°定理的关键找“平面的垂线”.
三、知识运用
例1. 如图,PD⊥平面ABC,AC=BC,D为AB的中点,求 证AB⊥PC.
证明: ∵ PD⊥平面ABC,
∴ DC为PC在平面的射影,
而△ABC为等腰三角形, A
D为AB的中点,
求点到线的距离,二面角大小, 3.证明程序分三个步骤:“一垂二射三证”,
计算程序分三个步骤:“一作二证三算”.
已知:如图,PO为平面α的斜线, PA⊥α ,
a在平面α内且垂直PO的射影AO.
P
求证:a⊥POa来自证明:PA⊥α ①
Ao α
aα
PA⊥a
AO⊥a
②
a⊥平面PAO
PA∩AO=A
PO 平面PAO
③
a⊥PO
① 线面垂直
② 线线垂直
③ 线面垂直
线线垂直
性质定理
判定定理
性质定理
说明:
1、三垂线定理描述的是斜线、射影、直线之间 的垂直关系.
∵BC是AC的射影,且CD⊥BC,∴CD⊥AC (三垂线定理) 因此斜线AC的长度就是电塔顶A与道路的距离。
A
B
90°
C
再在道路边取一点D,使∠CDB=45°, 则CD=CB
可测得C、D的距离等于a米, ∴BC= a米,
在直角△ABC中, AC2=AB2+BC2, AC= 152+a2 米
答:电塔顶A与道路的距离是 152 a2米。
P C
D
B
∴ AB ⊥ CD
∴ AB ⊥PC
例2.如图,已知正方体ABCD-A1B1C1D1中,连结 BD1,AC,CB1,B1A,求证:BD1⊥平面AB1C
证明:连结BD、 A1B
D1
∵DD1⊥平面ABCD
A1
∴BD是斜线D1B在平面ABCD上的射影
∵ABCD是正方形∴AC⊥BD
C1 B1
(AC垂直射影BD),∴AC⊥BD1
A
B
90°
C
45° ●D
例4.如图,长方体 ABCD-A1B1C1D1中,AB=AD=2 2 ,
AA1= 3, E,F分别为AB和AD的中点,求平面A1EF
和平面ABCD所成二面角的大小?
解: 连接BD,AC,AC交EF于G, 连接A1G
D
1
C1
∵底面ABCD是正方形,∴AC⊥BD, A1 而E,F为AB和AD中点, ∴EF∥BD, ∴ EF⊥AC
2、a与PO可以相交,也可以异面.
3、三垂线定理的实质是平面的一条斜线和
平面内的一条直线垂直的判定定理.
4 、转化思想:空间两直线的垂直问题转化为平面内
两直线的垂直问题.
P
oa
α
A
练习:判定下列命题是否 正确
α
P
oa A
(1)若a是平面α的斜线、直线b垂直于a在平面
α内的射影,则a⊥b。
( ×)
(2)若a是平面α的斜线,b是平面α内的直线,
又因为AG为A1G在平面ABCD 上的射影.(由三垂线定理)
D F
∴ EF⊥A1G,则∠A1GA为二面角的平 面角.
A
G E
B1 C
B
计算得:二面角的大小为:60o
四、小 结
三垂线定理:在平面内的一条直线,如果 和这个平面的一条斜线的射影垂直,那么它也 和这条斜线垂直。
1.定理中四条线均针对同一平面而言, 2.定理的主要应用:证明线线垂直,线面垂直,
三垂线定理及其应用
P
oa
α
A
一、三线概念: 平面的斜线、垂线、射影
P
oa
α
A
如图PO是平面α的斜线, O为斜足; PA是平面α 的垂线, A为垂足; AO 是PO在平面α内的射 影.
二、三垂线定理:在平面内的一条直线(a),如果和这个平面 的一条斜线(PO)的射影(AO)垂直,那么它(a)也和这条斜线垂直。
