三垂线定理
合集下载
高二数学 三垂线定理
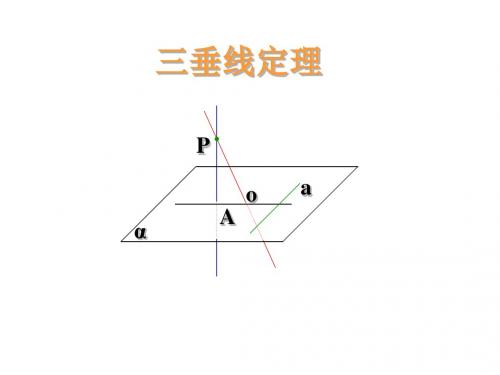
证明: PO , a ,
PO a.
又 PA a, PA PO P,
P
O
A
a
a 平面PAO. a AO
α
例题分析：
例1、已知点O是△ABC的BC边的高上的任 意一点，且PO⊥平面ABC，求证PA ⊥BC。
证明： ∵PO⊥平面ABC
P
A ∴ OA是PA在平面 O ABC内的射影， B 又∵BC⊥OA， ∴BC ⊥PA（三垂线定理）
AB OE, AC OF PE PF , PO PO,
OE OF .
Rt PEO Rt PFO.
又AO AO, Rt EAO RtFAO.
(三垂线定理的逆定理)
P
B E
BAO CAO.
A F
O C
课堂练习
如图，PD⊥平面ABC，AC=BC，D为AB 1、
OA是PA在内的射影,a ，且a OA.
证明: PO , a ,
PO a.
又 a OA, PO OA O,
P O A
求证:a PA.
a 平面POA. a PA.
a
α
三垂线定理
对三垂线定理的说明： 1、三垂线定理描述的是 PA(斜线)、OA(射影)、a(直线) α 之间的垂直关系，它们都是相对 同一个平面而言的。
三垂线定理
复习回顾
下图中哪些直线是平面的斜线、直线的射影？
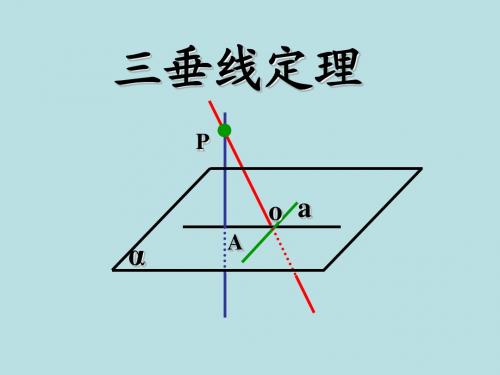
已知直线PO是平面α的垂线, O为垂足;
直线PA是平面α的斜线, A 为斜足; 直线OA是PA在平 面α内的射影.
P
A
a
α
O
如果a , a OA,
三垂线定理
1. 在正方体AC1中,E,G分别是AA1和 是 所 1 P CC1的中点, F在AB上,且C1E⊥EF, PD 成 AB 则EF与GD所成的角的大小为( D ) 边 的 上 (A) 30° (B) 45° (C) 60°(D) 90° 角 的 D1 是 一 C1 EB1是EC1在平面AB1 EC AB 多 点 内的射影 A1 少 求 B1 G ? 异 EB1 ⊥EF E D 面 M C DG‖AM‖EB1 直 EF ⊥DG A 线 B F B1C
F D O B E
C
思考题:在四面体ABCD中,已知 ⊥CD, 思考题:在四面体 中 已知AB⊥ , AC⊥BD,求证:AD⊥BC 求证: ⊥ ⊥ 求证 证明: 于点O, 证明:作AO⊥平面 ⊥平面BCD于点 , 于点 连接BO, , 连接 ,CO,DO,则BO, , , A CO,DO分别为 ,AC, 分别为AB, , , 分别为 AD在平面 在平面BCD上的射影. 上的射影. 在平面 上的射影 ∵AB⊥CD,∴BO⊥CD, ⊥ , ⊥ , 同理CO⊥BD, ⊥ , 同理 的垂心, 于是O是 于是 是△BCD的垂心, 的垂心 ∴DO⊥BC,于是 ⊥BC. ⊥ ,于是AD⊥ B O C D
例2 如果一个角所在平面外一点到角 的两边距离相等, 的两边距离相等,那么这一点在平面 上的射影在这个角的平分线上. 上的射影在这个角的平分线上.
四,两个重要结论
练.(1)已知四面体 ( )已知四面体P-ABC, PA,PB,PC两两垂直,求证: 两两垂直, , , 两两垂直 求证: P在平面 在平面ABC内的射影是 在平面 内的射影是 A △ABC的垂心. 的垂心. 高的交点) (高的交点)
五,知识方法总结
1,三垂线定理及逆定理. 三垂线定理及逆定理. 作用:用于证明线线垂直. 2,作用:用于证明线线垂直. 用法:先找线面垂直, 用法:先找线面垂直,再找线射 垂直,从而推出线斜( (斜)垂直,从而推出线斜(射) 垂直. 垂直.平面可能水平放置也可能竖 直或倾斜放置. 直或倾斜放置. 3,两个射影结论. 两个射影结论.
三垂线定理和逆定理
O
C
同理，AC⊥BD
平面ABCD
AC是PC在ABCD上的射影
∴ PC⊥BD
∴ PO⊥BD
P
(2) 已知：PA⊥平面PBC，PB=PC，
M是BC的中点， 求证：BC⊥AM 证明: ∵ PA⊥平面PBC
C A
∴ PM是AM在平面PBC上的射影
∵ PB=PC
M B
M是BC的中点
∴ PM ⊥BC 又 BC 平面PBC ∴ BC⊥AM
O
a
α
A
三垂线定理
说明：
1、三垂线定理描述的是PO(斜线)、AO(射
影)、a(直线)之间的垂直关系。 2、a与PO可以相交，也可以异面。 3、三垂线定理的实质是平面的一条斜线和 平面内的一条直线垂直的判定定理。
例1 直接利用三垂线定理证明下列各题：
(1) 已知：PA⊥正方形ABCD所在平面，O为对角线BD的中点 求证：PO⊥BD，PC⊥BD (2) 已知：PA⊥平面PBC，PB=PC，M是BC的中点， 求证：BC⊥AM
C
我们要学会从纷繁的已知条件中找出 或者创造出符合三垂线定理的条件 P
解 题 回 顾
α
A1
A
O
a
α
P
A O
a
P
B1
C1 A M B C
C B
三垂线定理解题的关键：找三垂！
解 题 回 顾
怎么找？
一找直线和平面垂直 二找平面的斜线在平面 内的射影和平面内的 一条直线垂直 P
α
A
O
a
注意：由一垂、二垂直接得出第三垂 并不是三垂都作为已知条件
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC， PO⊥ ，垂足分别是E、F、O，PE=PF P 求证：∠BAO=∠CAO 分析： 要证 ∠BAO=∠CAO 只须证OE=OF, OE⊥AB,OF⊥AC
三垂线定理
二、应用举例 例题1，在空间四边形ABCD中，点A在平面BCD内
的射影O1是三角形BCD的垂心。 求证：B在平面ACD内的射影O2是三角形ACD 的垂心 (练)如图所示，已知AB CD, AC BD.求证：AD BC
A
D B
C
例题2，在正方体AC1中，EF是异面直线AC与A1D的
公垂线，求证EF//BD1
D1 C1
A1 B1
设PA、PB、PC两两互相垂直，且PA=3，PB=4， PC=6，求点P到平面ABC的距离。
P
A H B
C E
例3、道旁有一条河，彼岸有电塔AB，
高15m，只有测角器和皮尺作测量工具， A
能否求出电塔顶与道路的距离？
B
90°
C
45°
D
例题5，长方体ABCD-A1B1C1D1中，AB=a。 BC=BB1=b。求点C到直线AB1的距离
三 垂 线 定 理2
P
oa
α
A
二、两个基本定理回顾
1，三垂线定理：在平面内的一条直线，和这个平面 的一条斜线的射影垂直，那么它也和这条斜线垂直。
OA是PA在平面内的射影
P
a
a
a OA
OA α
a PA
2,三垂线定理的逆定理 在平面内的一条直线，如果和这个平面的一
条斜线垂直，那么，它也和这条斜线的射影垂直。
；
的事。 ? 她不属于我们，因为她是天使。 是“国家”错了 ? 在民法的慈母般的眼里，每一个人就是整个国家。——孟德斯鸠 1 ? 一百年前的法兰西。正义的一天—— ? 1898年1月13日，著名作家左拉在《震旦报》上发表致共和国总统的公开信，题为《我控诉》，将一宗为当局所讳的 冤案公曝天下，愤然以公民的名义指控“国家犯罪”，
【数学课件】三垂线定理
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底 部的距离为8米，求旗杆顶部A到楼底部的距离。
A 解：过B作楼底部所在直线 EF 的垂线BC 垂足为C，
F
C
B
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底 部的距离为8米，求旗杆顶部A到楼底部的距离。
A 解：过B作楼底部所在直线 EF 的垂线BC 垂足为C，
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底 部的距离为8米，求旗杆顶部A到楼底部的距离。
A 解：过B作楼底部所在直线 EF 的垂线BC 垂足为C，
由三垂线定理知EFAC
F
C
B
E
二、应用
例1.已知学校的旗杆高20米，测量得旗杆底部B到楼底 部的距离为8米，求旗杆顶部A到楼底部的距离。
证明：∵AC面，a 面
∴ACa
一、三垂线定理
1.三垂线定理：在平面内的一条直线，如果和这个平面的一条 A 斜线的射影垂直，那么它也和这条斜线垂直。
已知：AC和AB分别是平面的垂
线和斜线，BC是AB在平面
C
B
a
上的射影，a，aBC。 求证： aAB。
证明：∵AC面，a 面
∴ACa
∵BCa ，AC∩BC＝C
9.4 直线与平面垂直的判定和性质
————————————————————— —
§6 三垂线定理
教学目的
• 掌握三垂线定理及逆定理 • 运用三垂线定理及逆定理解决数学问题 • 在实际生活中运用三垂线定理及逆定理
重点与难点
•三垂线定理及逆定理的适用条件 •三垂线定理及逆定理的应用
三垂线定理
三垂线定理
P
o a
α
A
一、三线概念: 平面的斜线、垂线、射影 如图PO是平面α的斜线,
P
A
O为斜足; PA是平面α 的垂线, A为垂足; o
α
AO是PO在平面
α内的射影.
已知:如图,PO为平面α 的斜线,PA⊥α ,a在平 面α内且垂直PO 的射影AO. 求证:a⊥PO
P a α
A
o
已知:如图,PO为平面α的斜线, PA⊥α ,a在平面α内且垂直PO 的射影AO.求证:a⊥PO P a 证明: A o PA⊥α 线线垂直 α PA⊥a a α 线面垂直 AO ⊥ a 线面垂直 a⊥平面PAO
1 1
D1
C1
四、小
结
三垂线定理：在平面内的一条直线，如 果和这个平面的一条斜线的射影垂直， 那么它也和这条斜线垂直。
1.定理中四条线均针对同一平面而言,
2.定理的主要应用:证明线线垂直, 线面垂直, 3.证明程序分三个步骤:“一垂二射三证”
计算程序分三个步骤:“一作二证三算”
∴ DC为PC在平面的射影,
而△ABC为等腰三角形, D为AB的中点, ∴ AB ⊥ CD
P C
∴ AB ⊥PC A
D
B
例2.如图，已知正方体ABCD-A1B1C1D1中， 连结BD1，AC，CB1，B1A， 求证：BD1⊥平面AB1C
证明：连结BD、 A1B ∵DD1⊥平面ABCD A B ∴BD是斜线D1B在平面ABCD 上的射影 ∵ABCD是正方形 D C ∴AC⊥BD (AC垂直射影BD)， B A ∴AC⊥BD1 同理:BA1是斜线BD1在平面ABB1A1上的射 影 , AB1 ⊥ BD1而AC ∩AB1 =A ∴BD1⊥平面AB1C
P
o a
α
A
一、三线概念: 平面的斜线、垂线、射影 如图PO是平面α的斜线,
P
A
O为斜足; PA是平面α 的垂线, A为垂足; o
α
AO是PO在平面
α内的射影.
已知:如图,PO为平面α 的斜线,PA⊥α ,a在平 面α内且垂直PO 的射影AO. 求证:a⊥PO
P a α
A
o
已知:如图,PO为平面α的斜线, PA⊥α ,a在平面α内且垂直PO 的射影AO.求证:a⊥PO P a 证明: A o PA⊥α 线线垂直 α PA⊥a a α 线面垂直 AO ⊥ a 线面垂直 a⊥平面PAO
1 1
D1
C1
四、小
结
三垂线定理：在平面内的一条直线，如 果和这个平面的一条斜线的射影垂直， 那么它也和这条斜线垂直。
1.定理中四条线均针对同一平面而言,
2.定理的主要应用:证明线线垂直, 线面垂直, 3.证明程序分三个步骤:“一垂二射三证”
计算程序分三个步骤:“一作二证三算”
∴ DC为PC在平面的射影,
而△ABC为等腰三角形, D为AB的中点, ∴ AB ⊥ CD
P C
∴ AB ⊥PC A
D
B
例2.如图，已知正方体ABCD-A1B1C1D1中， 连结BD1，AC，CB1，B1A， 求证：BD1⊥平面AB1C
证明：连结BD、 A1B ∵DD1⊥平面ABCD A B ∴BD是斜线D1B在平面ABCD 上的射影 ∵ABCD是正方形 D C ∴AC⊥BD (AC垂直射影BD)， B A ∴AC⊥BD1 同理:BA1是斜线BD1在平面ABB1A1上的射 影 , AB1 ⊥ BD1而AC ∩AB1 =A ∴BD1⊥平面AB1C
三垂线定理应用
器和皮尺作测量工具，能否求出电塔顶与道路的距离？ 解：在道边取一点C， 使BC与道边所成水平角等于90°， 再在道边取一点D， 使水平角CDB等于45°， 测得C、D的距离等于20cm A
B
90°
C
45°
D
三垂线定理
∵BC是AC的射影
且CD⊥BC
∴CD⊥AC
因此斜线AC的长度就是电塔顶与道路的距离。 ∵∠CDB=45°，CD⊥BC，CD=20cm 答：电塔顶与道路的距离是25m。
三垂线定理：在平面内的一条直线，如果它和这个平 面的一条斜线的射影垂直，那么它也和这条斜线垂直。 已知:PO,PA分别是平面α的垂线,斜线,OA是PA 在 α内的射影,a 求证: a ⊥PA. α,且a ⊥OA.
P
A a O α
三垂线定理的逆定理：在平面内的一条直线，如果 它和这个平面的一条斜线垂直，那么它也和这条斜 线在平面内的射影垂直。
A
B∴BC=20m， Nhomakorabea在直角三角形ABC中 AC2=AB2+BC2，AC= 152+202 =25(cm)
90°
C
45°
D
证明:∵AH⊥平面BCD，
A
∴BH为斜线AB在
平面BCD上的射影. B ∵AB⊥CD.
∵CD 平面BCD，
D
H C
∴BH⊥CD.
4、在空间四边形ABCD中AB⊥CD, AC⊥BD, A 求证:BC⊥CD
.
B
D
C
二、应用:
1、有一方木料如图,上底 有一点E,要经过点E在上底 面内画一条直线和C,E的连 线垂直,应怎样画?
“一垂二射三证明” “一垂”:找平面及平面的垂线 “二射”:找斜线在平面上的射影 “三证明”:用定理证明直线垂直
B
90°
C
45°
D
三垂线定理
∵BC是AC的射影
且CD⊥BC
∴CD⊥AC
因此斜线AC的长度就是电塔顶与道路的距离。 ∵∠CDB=45°，CD⊥BC，CD=20cm 答：电塔顶与道路的距离是25m。
三垂线定理：在平面内的一条直线，如果它和这个平 面的一条斜线的射影垂直，那么它也和这条斜线垂直。 已知:PO,PA分别是平面α的垂线,斜线,OA是PA 在 α内的射影,a 求证: a ⊥PA. α,且a ⊥OA.
P
A a O α
三垂线定理的逆定理：在平面内的一条直线，如果 它和这个平面的一条斜线垂直，那么它也和这条斜 线在平面内的射影垂直。
A
B∴BC=20m， Nhomakorabea在直角三角形ABC中 AC2=AB2+BC2，AC= 152+202 =25(cm)
90°
C
45°
D
证明:∵AH⊥平面BCD，
A
∴BH为斜线AB在
平面BCD上的射影. B ∵AB⊥CD.
∵CD 平面BCD，
D
H C
∴BH⊥CD.
4、在空间四边形ABCD中AB⊥CD, AC⊥BD, A 求证:BC⊥CD
.
B
D
C
二、应用:
1、有一方木料如图,上底 有一点E,要经过点E在上底 面内画一条直线和C,E的连 线垂直,应怎样画?
“一垂二射三证明” “一垂”:找平面及平面的垂线 “二射”:找斜线在平面上的射影 “三证明”:用定理证明直线垂直
三垂直定理立体几何
三垂直定理立体几何三垂线定理（也称三垂直定理）是立体几何中一个重要的定理，通常用于计算三角形的面积或其他几何量。
在三维空间中，如果一个点P在三角形ABC所在平面上，那么它到三角形的三个顶点的连线所在的直线都与三角形的平面垂直。
换句话说，点P到三角形的三个边AB、BC、CA 所在平面的距离都是垂直距离。
证明：设点P在平面ABC上，向量a、b、c分别表示边向量AB、BC、CA，则向量n=a×b表示平面ABC的法向量（叉积）。
点P到平面ABC的距离（设为h）满足n·OP=h|n|，其中OP 为点P到原点O的向量。
考虑向量PA在向量n上的投影PA'，即PA'=(PA·n/|n|)n/|n|。
根据余弦公式，PA·PB=PA^2+PB^2-AB^2/2，因此PA·n=PA·(a×b)=PA·c^2/2SABC。
将上述若干式子代入n·OP=h|n|中，得到PA'=PA·c^2/(2SABC)|n|/|c×(PA×c)|同理，PB'和PC'也可以表示为三垂线上的垂直距离分别为h=PA'，h=PB'和h=PC'。
应用：利用三垂线定理，可以方便地计算三角形的面积。
设三角形ABC的三边长分别为a、b、c，其半周长为s=(a+b+c)/2，则三角形的面积S可以表示为S=abc/4R=1/2absinC=1/2crsinA=1/2basinC其中R为三角形外接圆半径，A、B、C为三角形的角度。
由于三条垂线的长度都可以用三条边的长度表示，因此可以通过这些式子计算出三角形的面积。
三垂线还可以用于计算三角形垂心（三条垂线交点）、oktane棱锥的体积等相关几何量。
需要注意的是，在三维空间中绝大多数点不在三角形所在平面上，因此计算其垂距要用到点到平面的距离公式。
三垂线定理
P
A H B
C E
例3、道旁有一条河，彼岸有电塔AB，
高15m，只有测角器和皮尺作测量工具， A
能否求出电塔顶与道路的距离？
B
90°
C
45°
D
例题5，长方体ABCD-A1B1C1D1中，AB=a。 BC=BB1=b。求点C到直线AB1的距离
D1 C1
A1 B1
D
C
A
B
例 如果一个角所在平面外一点到角的两边距离相等， 那么这一点在平面上的射影在这个角的平分线上。
(A) 30° (B) 45° (C) 60°(D) 90° D1
C1
A1
B1 G
ED
C
A F
B
3）如图在斜三棱柱ABC-A1B1C1中，已知ABC是
正三角形AA1=2, ∠A1AB=∠A1AC=600，
求此三棱柱的高
A1
B1 C1
A
C
B
二、应用举例 例题1，在空间四边形ABCD中，点A在平面BCD内
一基础训练题
1）P是边长为a的正六边形AB PA⊥AF。为求P与CD的距离，作PQ⊥CD
于Q点，则
（） C
A、Q为CD的中点
B、Q与D重合
C、 Q与C重合
D、以上都不对
2)在正方体AC1中，E、G分别是AA1和CC1的中点， F在
AB上，且C1E⊥EF， 则EF与GD所成的角的大小为( D ）
已知：∠BAC在平面内，点P，PE⊥AB， P
PF⊥AC，PO⊥ ，垂足分别是
E、F、O，PE=PF 求证：∠BAO=∠CAO
EB
A
O
FC
思考：1）若∠PAE=∠PAF,则点P的射影在那里 2）若点P到 BAF的三个顶点距离相等点P的射影是
A H B
C E
例3、道旁有一条河，彼岸有电塔AB，
高15m，只有测角器和皮尺作测量工具， A
能否求出电塔顶与道路的距离？
B
90°
C
45°
D
例题5，长方体ABCD-A1B1C1D1中，AB=a。 BC=BB1=b。求点C到直线AB1的距离
D1 C1
A1 B1
D
C
A
B
例 如果一个角所在平面外一点到角的两边距离相等， 那么这一点在平面上的射影在这个角的平分线上。
(A) 30° (B) 45° (C) 60°(D) 90° D1
C1
A1
B1 G
ED
C
A F
B
3）如图在斜三棱柱ABC-A1B1C1中，已知ABC是
正三角形AA1=2, ∠A1AB=∠A1AC=600，
求此三棱柱的高
A1
B1 C1
A
C
B
二、应用举例 例题1，在空间四边形ABCD中，点A在平面BCD内
一基础训练题
1）P是边长为a的正六边形AB PA⊥AF。为求P与CD的距离，作PQ⊥CD
于Q点，则
（） C
A、Q为CD的中点
B、Q与D重合
C、 Q与C重合
D、以上都不对
2)在正方体AC1中，E、G分别是AA1和CC1的中点， F在
AB上，且C1E⊥EF， 则EF与GD所成的角的大小为( D ）
已知：∠BAC在平面内，点P，PE⊥AB， P
PF⊥AC，PO⊥ ，垂足分别是
E、F、O，PE=PF 求证：∠BAO=∠CAO
EB
A
O
FC
思考：1）若∠PAE=∠PAF,则点P的射影在那里 2）若点P到 BAF的三个顶点距离相等点P的射影是
2.3.1-3三垂线定理
O
O为BD的中点
∴ AO⊥BD 又AO是PO在ABCD上的射影
C
PO⊥BD
同理，AC⊥BD
AO是PO在ABCD上的射影
PC⊥BD
例3:在四面体ABCD中，已知AB⊥CD，AC⊥BD 求证：AD⊥BC
证明：作AO⊥平面BCD于点O， 连接BO，CO，DO，则BO， CO，DO分别为AB，AC， AD在平面BCD上的射影。
证明：∵ P 是平面ABC 外一点 P
PA⊥平面ABC
∴PC是平面ABC的斜线 ∴AC是PC在平面ABC上的射影 ∵BC平面ABC 且AC ⊥ BC ∴由三垂线定理得 A B
C
PC ⊥ BC
例2 PA⊥正方形ABCD所在平
P A B D
面，O为对角线BD的中点，
求证：PO⊥BD，PC⊥BD 证明: ∵ABCD为正方形
a
6、两定理可用符号语言表示 如下：
设 l 是平面 的斜线，l ' 是直线 l 在平面 内的射 影，a 则
P
l
A
l
'
O
a
al al
'
7、定理的作用
（1）作图中是作二面角的平面角的主要依据。 （2）在证题时是证线线垂直的好方法。 （3）在计算时用归面法归拢已知条件，便于计算。
8、三垂线定理解题的关键： 定面、找线！怎么找？
P
α
A
Oa
三垂线定理总结
（1）定理涉及到的五个元素是 “一面四线” （2）三垂线定理（或逆定理），实质上是平面的一条斜线 （或其射影）和平面内的一条直线垂直的判定定理，这两条 直线可以是相交直线，也可以是异面直线 （3）定理的证明思路是：
三垂线定理及其逆定理的应用
三垂线定理及其 逆定理应用
P
o
α A
a
复习：
三垂线定理：
在平面内的一条直线，如果和这个平面的一条斜线 的射影垂直，那么它也和这条斜线垂直。
三垂线定理的逆定理：
在平面内的一条直线，如果和这个 平面的一条斜线垂直，那么它也和 这条斜线的射影垂直。
P o a
α 三垂线定理及其逆定理可表述为：
A
设l 为平面α的斜线， l ′是l 在平面α内的射影， 直线a α ，则 a ⊥ l ′ a⊥l。
例3、把一个直角∠AOC按它的角平线OB折 叠，使OC在平面AOB上的射影为OB，则折后 ∠AOC等于多少？
P
θ1 θ2
C
O
θ
D
B
α
E A
600
例 4 ABCD 是矩形， 过 CD 的平面交 （ 1）求证：
PA 面 ABCD ，
PA ， PB 于 E 、 F ，
CDEF 是直角梯形；
例⒈ 已知PD⊥平面ABCD，下列条件中 ⑴ 四边形ABCD是菱形； ⑵ 四边形ABCD是矩形； ⑷若四边形ABCD是矩形， 且PD = a ，AB = b,BC = c， 求P到AB及AC的距离。 ⑵⑶ ⑴⑶
2 2
⑶ 四边形ABCD是正方形。
能使BC ⊥PC一定成立的序号有 能使AC ⊥PB一定成立的序号有 P
三垂线定理的逆定理：在平面内的一条直线，如果和这个
1°定理中四条线均针对同一平面而言
2°应用定理关键是找“基准面”这个参照系 3°操程序分三个步骤——“一垂二射三证”
两定理特征：四线一面三垂直
（ 2）当 PA AB a ， BC b ， E 、 F 分别是 PA 、 PB 的中点，且梯形的面积 是矩形面积的 5 4 时，求 a ： b 的值。
P
o
α A
a
复习：
三垂线定理：
在平面内的一条直线，如果和这个平面的一条斜线 的射影垂直，那么它也和这条斜线垂直。
三垂线定理的逆定理：
在平面内的一条直线，如果和这个 平面的一条斜线垂直，那么它也和 这条斜线的射影垂直。
P o a
α 三垂线定理及其逆定理可表述为：
A
设l 为平面α的斜线， l ′是l 在平面α内的射影， 直线a α ，则 a ⊥ l ′ a⊥l。
例3、把一个直角∠AOC按它的角平线OB折 叠，使OC在平面AOB上的射影为OB，则折后 ∠AOC等于多少？
P
θ1 θ2
C
O
θ
D
B
α
E A
600
例 4 ABCD 是矩形， 过 CD 的平面交 （ 1）求证：
PA 面 ABCD ，
PA ， PB 于 E 、 F ，
CDEF 是直角梯形；
例⒈ 已知PD⊥平面ABCD，下列条件中 ⑴ 四边形ABCD是菱形； ⑵ 四边形ABCD是矩形； ⑷若四边形ABCD是矩形， 且PD = a ，AB = b,BC = c， 求P到AB及AC的距离。 ⑵⑶ ⑴⑶
2 2
⑶ 四边形ABCD是正方形。
能使BC ⊥PC一定成立的序号有 能使AC ⊥PB一定成立的序号有 P
三垂线定理的逆定理：在平面内的一条直线，如果和这个
1°定理中四条线均针对同一平面而言
2°应用定理关键是找“基准面”这个参照系 3°操程序分三个步骤——“一垂二射三证”
两定理特征：四线一面三垂直
（ 2）当 PA AB a ， BC b ， E 、 F 分别是 PA 、 PB 的中点，且梯形的面积 是矩形面积的 5 4 时，求 a ： b 的值。
三垂线定理及其应用
∵BC是AC的射影,且CD⊥BC,∴CD⊥AC (三垂线定理) 因此斜线AC的长度就是电塔顶A与道路的距离。 A B
90°
C
再在道路边取一点D，使∠CDB=45°, 则CD=CB
可测得C、D的距离等于a米,
在直角△ABC中,
∴BC= a米，
AC2=AB2+BC2， AC= 152+a2
米
答：电塔顶A与道路的距离是 15 2 a 2米。
A D B C
同理:BA1是斜线BD1在平面ABB1A1上的射影 , AB1 ⊥ BD1 而AC ∩AB1 =A ∴BD1⊥平面AB1C
例3.道路旁有一条河，彼岸有电塔AB，高15m，只有测角 器和皮尺作测量工具，不过河能否求出电塔顶A与道路的 距离？(测角器只能测水平面角) 解：在道路边取一点C， 使BC与道边所成水平角等于90°，
三垂线定理及其应用
P A o
a
α
一、三线概念: 平面的斜线、垂线、射影
如图PO是平面α的斜线,
P
A
O为斜足; PA是平面α 的垂线, A为垂足; AO
o
a
是PO在平面α内的射 影.
α
二、三垂线定理：在平面内的一条直线(a)，如果和这个平面 的一条斜线(PO)的射影(AO)垂直，那么它(a)也和这条斜线垂直。 已知:如图,PO为平面α的斜线, PA⊥α , a在平面α内且垂直PO的射影AO. 求证:a⊥PO
( ×) (×)
(2)若a是平面α 的斜线，b是平面α 内的直线，
2°定理的关键找“平面的垂线”.
三、知识运用 例1. 如图,PD⊥平面ABC,AC=BC,D为AB的中点,求 证AB⊥PC.
证明: ∵ PD⊥平面ABC, ∴ DC为PC在平面的射影, 而△ABC为等腰三角形, D为AB的中点,
90°
C
再在道路边取一点D，使∠CDB=45°, 则CD=CB
可测得C、D的距离等于a米,
在直角△ABC中,
∴BC= a米，
AC2=AB2+BC2， AC= 152+a2
米
答：电塔顶A与道路的距离是 15 2 a 2米。
A D B C
同理:BA1是斜线BD1在平面ABB1A1上的射影 , AB1 ⊥ BD1 而AC ∩AB1 =A ∴BD1⊥平面AB1C
例3.道路旁有一条河，彼岸有电塔AB，高15m，只有测角 器和皮尺作测量工具，不过河能否求出电塔顶A与道路的 距离？(测角器只能测水平面角) 解：在道路边取一点C， 使BC与道边所成水平角等于90°，
三垂线定理及其应用
P A o
a
α
一、三线概念: 平面的斜线、垂线、射影
如图PO是平面α的斜线,
P
A
O为斜足; PA是平面α 的垂线, A为垂足; AO
o
a
是PO在平面α内的射 影.
α
二、三垂线定理：在平面内的一条直线(a)，如果和这个平面 的一条斜线(PO)的射影(AO)垂直，那么它(a)也和这条斜线垂直。 已知:如图,PO为平面α的斜线, PA⊥α , a在平面α内且垂直PO的射影AO. 求证:a⊥PO
( ×) (×)
(2)若a是平面α 的斜线，b是平面α 内的直线，
2°定理的关键找“平面的垂线”.
三、知识运用 例1. 如图,PD⊥平面ABC,AC=BC,D为AB的中点,求 证AB⊥PC.
证明: ∵ PD⊥平面ABC, ∴ DC为PC在平面的射影, 而△ABC为等腰三角形, D为AB的中点,
三垂线定理教学课件
0P和CP垂直，怎样做？
分析：
CP在木块内部，直接做难，
若在同一平面内，易做两条
直线垂直。
利用定理将问题转化为同一
个平面内解决
D1
·
P
A1
C1
B1
D
A
C
B
D1
C1
B1
A1
D
A
C
B
D1
C1
B1
A1
D
A
C
B
三垂线定理
三垂线定理的逆定理 ·P
⊥
·A ·O
⊥
线垂直。
P
C
D
B
A
D1
A1
C1
B1
正方体
思考：
（1） “三”指的是什么，
“垂”指的什么.
（2）为何强调平面内？
A
O
三垂线定理
在平面内的一条直线，如果和这个平面的
一条斜线的射影垂直，那么它也和这条斜
线垂直。
P
D
C
B
A
D1
A1
C1
是什么，
“垂”指的什么.
（2）为何强调平面内？
A
O
例1.判断：若一条直线垂直于平
面内的无数条直线，那么这条直线
垂直这个平面.（ ）
三垂线定理的逆定理
在平面内的一条直线，如果和这个平面的
一条斜线垂直，那么它也和这条斜线的射
影垂直。
·P
PA
PO
·
·
O
A
AO
⊥
⊥
例2．如图正方体木块
儿的上底面A1C1 内有一
分析：
CP在木块内部，直接做难，
若在同一平面内，易做两条
直线垂直。
利用定理将问题转化为同一
个平面内解决
D1
·
P
A1
C1
B1
D
A
C
B
D1
C1
B1
A1
D
A
C
B
D1
C1
B1
A1
D
A
C
B
三垂线定理
三垂线定理的逆定理 ·P
⊥
·A ·O
⊥
线垂直。
P
C
D
B
A
D1
A1
C1
B1
正方体
思考：
（1） “三”指的是什么，
“垂”指的什么.
（2）为何强调平面内？
A
O
三垂线定理
在平面内的一条直线，如果和这个平面的
一条斜线的射影垂直，那么它也和这条斜
线垂直。
P
D
C
B
A
D1
A1
C1
是什么，
“垂”指的什么.
（2）为何强调平面内？
A
O
例1.判断：若一条直线垂直于平
面内的无数条直线，那么这条直线
垂直这个平面.（ ）
三垂线定理的逆定理
在平面内的一条直线，如果和这个平面的
一条斜线垂直，那么它也和这条斜线的射
影垂直。
·P
PA
PO
·
·
O
A
AO
⊥
⊥
例2．如图正方体木块
儿的上底面A1C1 内有一
三垂线逆定理
3.经过一个角的顶点引这个角 所在平面的斜线，如果斜线和 这个角两边的夹角相等，那么 斜线在平面上的射影是这个角 的平分线所在的直线。 B C
C1
H
A
B1
4.在ABCD—A1B1C1D1中， 求证：AC1⊥平面B A1 D
D1
C D
A1
B A定理来自逆定理线斜垂直线射垂直
定 理 逆 定 理
在平面 内的一条直线，如果和这个平 面的一条斜线的射影垂直，那 么，它就和这条斜线垂直。
三垂线定理的逆定理
在平面内的一条直线，如果和 这个平面的一条斜线垂直，那 么，它也和这条斜线的射影垂 直。
线斜垂直
例3 如果一个角所在平面外一点到角的两边距离相等， 那么这一点在平面上的射影在这个角的平分线上。
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC， PO⊥ ，垂足分别是E、F、O，PE=PF P 求证：∠BAO=∠CAO 分析： 要证 ∠BAO=∠CAO E B 只须证OE=OF, OE⊥AB,OF⊥AC O
证明： ∵ PO ⊥ F ∴OE、OF是PE、PF在内的射影 ∴ OE=OF ∵ PE=PF 由OE是PE的射影且PE⊥AB OE⊥AB 同理可得OF⊥AC
三垂线逆理
三垂线定理包含几种垂直关系？
①线面垂直 ②线射垂直 ③ 线斜垂直
P A O P P O
α
a
α
A
a
α
A
O
a
直 线 和
平面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
三垂线定理的逆定理
线射垂直
α
P A O
a
？
α
P A
线斜垂直
C1
H
A
B1
4.在ABCD—A1B1C1D1中， 求证：AC1⊥平面B A1 D
D1
C D
A1
B A定理来自逆定理线斜垂直线射垂直
定 理 逆 定 理
在平面 内的一条直线，如果和这个平 面的一条斜线的射影垂直，那 么，它就和这条斜线垂直。
三垂线定理的逆定理
在平面内的一条直线，如果和 这个平面的一条斜线垂直，那 么，它也和这条斜线的射影垂 直。
线斜垂直
例3 如果一个角所在平面外一点到角的两边距离相等， 那么这一点在平面上的射影在这个角的平分线上。
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC， PO⊥ ，垂足分别是E、F、O，PE=PF P 求证：∠BAO=∠CAO 分析： 要证 ∠BAO=∠CAO E B 只须证OE=OF, OE⊥AB,OF⊥AC O
证明： ∵ PO ⊥ F ∴OE、OF是PE、PF在内的射影 ∴ OE=OF ∵ PE=PF 由OE是PE的射影且PE⊥AB OE⊥AB 同理可得OF⊥AC
三垂线逆理
三垂线定理包含几种垂直关系？
①线面垂直 ②线射垂直 ③ 线斜垂直
P A O P P O
α
a
α
A
a
α
A
O
a
直 线 和
平面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
三垂线定理的逆定理
线射垂直
α
P A O
a
？
α
P A
线斜垂直
三垂线定理
C
B
例1、已知在直三棱柱ABC A1B1C1中,ACB 900 , AC AA1，求证 AB1 A1C
A1 B1
C1
A
B
C
例2、在正方体ABCD A1B1C1D1中,F为CC1的中点， O是下底面ABCD的中心，求证AO 平面BDF 1
D1 A1 B1 C1
F
D A
O B
三垂线定理
基本概念
P
斜线 B
A
斜线长定理
PA PB OA OB PAO PBO
P
若PA=PB=PC，则P在面ABC上的射影 O是三角形ABC的_______-
A C
若直线l与平面 所成角 ，直线a在平面 3 内，且与直线l异面，则直线l与直线a所 成的角的取值范围是（ ） 2 2 2 A[0， ] B[ ， ] C[ ， ] D[ ， ] 3 3 3 2 3 3 2
PA A, m , PO , m PA m AO
P
若PD AB, PE AC , PF BC分别于 D, E, F , 且PD PE PF , 则P在面ABC 上的射影O是ABC的________。
P
A D
E
O
C F B
A O
C
若PA PB PC , 则P在面ABC上的 射影O是ABC的________。
A B
O
B
P a l O
斜线和平面所成的角是斜线和平面内任何直线所成的最小角
三垂线定理：
在平面内的一条直线，如果和这个平面的一条斜线在这个平 面内的射影垂直，那么它和这条斜线垂直 P
PA A, m , PO , m AO m PA
三垂线定理
O
a
α
A
三垂线定理
说明：
1、三垂线定理描述的是 三垂线定理 PO(斜线)、AO(射
影)、a(直线)之间的垂直关系。 P
A 2、a与PO可以相交，也可以异面。 α o a
3、三垂线定理的实质是平面的一条斜线和
江西省龙南中学 丁峤
平面内的一条直线垂直的判定定理。
三垂线定理
P A o
a
α
江西省龙南中学 丁峤
复习： 什么叫平面的斜线、垂线、射影？
三垂线定理
PO是平面α的斜线,
P
A
O为斜足; PA是平面α 的垂线, A为垂足; AO
o
a
是PO在平面α内的射
影. 如果a α, a⊥AO， 思考a与PO的位置关 系如何？
α
三垂线定理
三垂线定理：在平面内的一条直线，如果和这个平面的 一条斜线的射影垂直，那么它也和这条斜线垂直。
PA⊥α a α
PA⊥a ② a⊥平面PAO AO⊥a
P
a α
①
①
a⊥PO PO 平面PAO
③
A
o
②
③
线面垂直 性质
线线垂直
线面垂直 性质 判定定理
线线垂直
如果将定理“在 平面内”的条件去掉， 结论仍然成立吗？
例如：当 b⊥ 时， b⊥OA源自但 b不垂直于OPP
b
直线a 在一定要在平面 内，如果 a 不在平面内， 定理就不一定成立。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
求证： ；
证明：∵
∴ ，又∵
∴ 平面 ，
∴ ．
说明:(1)定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系；
(2)符号表达： .
(3)这两条直线可以是相交直线，也可以是异面直线.
2．三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直
说明：符号表达： ．
三、例题：
例1.已知：点 是 的垂心， ，垂足为 ，求证： ．
证明：∵点 是 的垂心，
∴
又∵ ，垂足为 ，
所以，由三垂线定理知， ．
例2.如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上
已知：∠BAC在α内，P，PEAB于E，PFAC于F且PE=PF，PO
求证：O在∠BAC的平分线上（即∠BAO=∠CAO）
证明：连接OE，OF∵PO
∴EO，FO分别为PE，PF在上的射影
∵PE=PF∴OE=OF∵PEAB，PFAC
∴OEAB，OFAC(三垂线定理的逆定理)
∴O到∠BAC两边距离相等
∴O在∠BAC的平分线上
变式：
已知： 在平面 内，点 ，垂足分别为 ，求证： ．
证明：∵ ，
∴ （三垂线定理逆定理）
∵ ，ห้องสมุดไป่ตู้ ，
三垂线定理
教学目标：
1.掌握三垂线定理及其逆定理的证明
2.正确地运用三垂线定理或逆定理证明两直线垂直
3.通过三垂线定理及三垂线逆定理的学习,渗透相对论观点
教学重点：三垂线定理及其逆定理的证明
教学难点：用三垂线定理及其逆定理证明两条异面直线的垂直
教学方法：启发式教学法
教 具：模具
教学过程
一、复习引入：
∴ ，又∵ ，∴
∴ ．
推广：经过一个角的顶点引这个角所在平面的斜线，如果斜线的这个角两边夹角相等，那么斜线在平面上的射影是这个角的平分线所在直线
例3.在三棱锥P-ABC中，三条侧棱PA，PB，PC两两垂直，H是△ABC的垂心
求证:(1)PH底面ABC(2)△ABC是锐角三角形.
证明:(1)略
(2)设AH与直线BC的交点为E，连接PE由(1)知PH底面ABC
1.直线与平面垂直的定义：
2.直线与平面垂直的判定定理：
3.平面的斜线，斜线在平面内的射影：
4.引入：若平面内一条直线与斜线的射影垂直，那么它和斜线垂直吗？
二、新授：
1.三垂线定理在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直
已知： 分别是平面 的垂线和斜线， 是 在平面 内的射影， ，且
∴AE为PE在平面ABC的射影，
由三垂线定理：PEBC
∵PBPC即△BPC是直角三角形，BC为斜边
∴E在BC边上 由于AEBC，故B∠C都是锐角
同理可证：∠A也是锐角∴△ABC为锐角三角形
四、练习：
1.边长为a的正六边形ABCDEF在平面内，PA⊥，PA=a，则P到CD的距离为，P
到BC的距离为.
2.AC是平面的斜线，且AO=a，AO与成60º角，OC，AA＇⊥于A＇，∠ OC=45º，
则A到直线OC的距离是，∠AOC的余弦值是.
答案：1. ;2.
3.如图，已知ABCD是矩形，AB=a，AD=b，PA平面ABCD，PA=2c，Q是PA的中点．
求（1）Q到BD的距离；（2）P到平面BQD的距离．
五、小结：三垂线定理及其逆定理的证明用三垂线定理及其逆定理的应用
六、作业：课本P2912,13.
补：平面α内有一正六边形,它的中心是O,边长是2 cm,OH⊥α,OH=4 cm,求点H到这个正六边形顶点和边的距离.
七、板书设计：
注意：(1)三垂线指涉及的四线中三个垂直关系PA，PO，AO都垂直α内的直线a其实质是：斜线和平面内一条直线垂直的判定和性质定理
(2)要考虑a的位置，并注意两定理交替使用
(3)注意三垂线定理及其逆定理中的“平面内”三个字的重要性.
(4)利用定理的关键要善于从各种图形中找出“平面的垂线”“平面的斜线”及“斜线的射影”.
证明：∵
∴ ，又∵
∴ 平面 ，
∴ ．
说明:(1)定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系；
(2)符号表达： .
(3)这两条直线可以是相交直线，也可以是异面直线.
2．三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直
说明：符号表达： ．
三、例题：
例1.已知：点 是 的垂心， ，垂足为 ，求证： ．
证明：∵点 是 的垂心，
∴
又∵ ，垂足为 ，
所以，由三垂线定理知， ．
例2.如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上
已知：∠BAC在α内，P，PEAB于E，PFAC于F且PE=PF，PO
求证：O在∠BAC的平分线上（即∠BAO=∠CAO）
证明：连接OE，OF∵PO
∴EO，FO分别为PE，PF在上的射影
∵PE=PF∴OE=OF∵PEAB，PFAC
∴OEAB，OFAC(三垂线定理的逆定理)
∴O到∠BAC两边距离相等
∴O在∠BAC的平分线上
变式：
已知： 在平面 内，点 ，垂足分别为 ，求证： ．
证明：∵ ，
∴ （三垂线定理逆定理）
∵ ，ห้องสมุดไป่ตู้ ，
三垂线定理
教学目标：
1.掌握三垂线定理及其逆定理的证明
2.正确地运用三垂线定理或逆定理证明两直线垂直
3.通过三垂线定理及三垂线逆定理的学习,渗透相对论观点
教学重点：三垂线定理及其逆定理的证明
教学难点：用三垂线定理及其逆定理证明两条异面直线的垂直
教学方法：启发式教学法
教 具：模具
教学过程
一、复习引入：
∴ ，又∵ ，∴
∴ ．
推广：经过一个角的顶点引这个角所在平面的斜线，如果斜线的这个角两边夹角相等，那么斜线在平面上的射影是这个角的平分线所在直线
例3.在三棱锥P-ABC中，三条侧棱PA，PB，PC两两垂直，H是△ABC的垂心
求证:(1)PH底面ABC(2)△ABC是锐角三角形.
证明:(1)略
(2)设AH与直线BC的交点为E，连接PE由(1)知PH底面ABC
1.直线与平面垂直的定义：
2.直线与平面垂直的判定定理：
3.平面的斜线，斜线在平面内的射影：
4.引入：若平面内一条直线与斜线的射影垂直，那么它和斜线垂直吗？
二、新授：
1.三垂线定理在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直
已知： 分别是平面 的垂线和斜线， 是 在平面 内的射影， ，且
∴AE为PE在平面ABC的射影，
由三垂线定理：PEBC
∵PBPC即△BPC是直角三角形，BC为斜边
∴E在BC边上 由于AEBC，故B∠C都是锐角
同理可证：∠A也是锐角∴△ABC为锐角三角形
四、练习：
1.边长为a的正六边形ABCDEF在平面内，PA⊥，PA=a，则P到CD的距离为，P
到BC的距离为.
2.AC是平面的斜线，且AO=a，AO与成60º角，OC，AA＇⊥于A＇，∠ OC=45º，
则A到直线OC的距离是，∠AOC的余弦值是.
答案：1. ;2.
3.如图，已知ABCD是矩形，AB=a，AD=b，PA平面ABCD，PA=2c，Q是PA的中点．
求（1）Q到BD的距离；（2）P到平面BQD的距离．
五、小结：三垂线定理及其逆定理的证明用三垂线定理及其逆定理的应用
六、作业：课本P2912,13.
补：平面α内有一正六边形,它的中心是O,边长是2 cm,OH⊥α,OH=4 cm,求点H到这个正六边形顶点和边的距离.
七、板书设计：
注意：(1)三垂线指涉及的四线中三个垂直关系PA，PO，AO都垂直α内的直线a其实质是：斜线和平面内一条直线垂直的判定和性质定理
(2)要考虑a的位置，并注意两定理交替使用
(3)注意三垂线定理及其逆定理中的“平面内”三个字的重要性.
(4)利用定理的关键要善于从各种图形中找出“平面的垂线”“平面的斜线”及“斜线的射影”.