位移和时间关系
2.3.1匀变速直线运动的位移与时间的关系

【知识拓展】
1 2
x at
2
因为位移公式是关于t的一元
二次函数,故x-t图象是一条抛物
线(一部分)。
注意:x-t图象不是物体运动的
轨迹,而是位移随时间变化的规律。
匀变速直线的位移-时间图像
【例3】有些汽车刹车后,停止转动的轮胎在地面上发生滑动,可以明
7 89
12t13t14
t
V
V
如果把整个运动过程分割得非常
非常细,很多很多小矩形的面积之和
就能非常精确地代表物体的位移了。
V0
0
t
t
这是物理上常用的微元法。
匀变速直线运动的位移仍可用图线与坐标轴所围的面积表示。
科学
方法
∆t 内是简单的匀速直线运动---- 化简
分割许多很小的时间间隔∆t---- 微分
站的加速度是多少?它还要行驶多远才能停下来?
解: 沿动车运动方向为正方向建立一维坐标系。把动车通过3000m
的运动称为前一过程,之后到停下来称为后一过程。
设在前一过程中的末位置为 M 点。初速度 v0 =126 km/h=35 m/s,
末速度vM=54 km/h=15 m/s,位移 x1 = 3000m。
匀速直线运动的位移就是v – t 图线
与坐标轴所夹的矩形“面积”
图象法
v/(m∙s-1)
v
v
x=v(t2-t1)/s
t1-t2时间内的位移
01. 匀速直线运动的位移
x1=12m
x2= -12m
v/m·s-1
x/m
10
匀速直线运动的v-t 图象中,图线与时间轴围
8
匀变速直线运动的位移与时间、速度的关系

匀变速直线运动的位移与时间、速度的关系【知识点归纳】1、匀变速直线运动位移与时间的关系的公式表达:2021at t v s += s 为t 时间内的位移。
当a=0时,t v s 0= 当v 0=0时,221at s =当a<0时,2021at t v s -= 可见2021at t v s +=是匀变速直线运动位移公式的一般表示形式,只要知道运动物体的初速度v 0和加速度a ,就可以计算出任意一段时间内的位移,从而确定任意时刻物体所在的位置。
位移公式也可以用速度——时间图像求出面积得位移而推出。
2、匀变速直线运动的位移和速度的关系as v v t 2202=-这个关系式是匀变速直线运动规律的一个重要的推论。
关系式中不含时间t ,在一些不涉及到时间的问题中,应用这个关系是较方便的。
3、匀变速直线运动的两个推论1.匀变速直线运动的物体在连续相等的时间(T)内的位移之差为一恒量。
公式:S 2-S 1=S 3-S 2=S 4-S 3=…=S n -S n-1=△S=aT2 2.某段时间中间时刻的瞬时速度等于这段时间的平均速度,即: v v t =2【案例分析】例1.某物体作变速直线运动,关于此运动下列论述正确的是( )A .速度较小,其加速度一定较小B .运动的加速度减小,其速度变化一定减慢C .运动的加速度较小,其速度变化一定较小D .运动的速度减小,其位移一定减小例2.火车从车站由静止开出做匀加速直线运动,最初一分钟行驶540米,则它在最初l0秒行驶的距离是( )A .90米B .45米C .30米D .15米例3一物体由静止沿光滑斜面匀加速下滑距离为L 时,速度为V ,当它的速度是v /2时,它沿全面下滑的距离是A .L /2 B.2L/2 C .L /4 D .3L /4例4:一物体以初速度v 1做匀变速直线运动,经时间t 速度变为v 2求:(1)物体在时间t 内的位移. (2)(3)比较vt/2和v s/2例5:一辆沿平直路面行驶的汽车,速度为36km/h .刹车后获得加速度的大小是4m/s 2,求:(1)刹车后3s 末的速度;(2)从开始刹车至停止,滑行一半距离时的速度.例6、一个质点作初速为零的匀加速运动,试求它在1s ,2s ,3s ,…内的位移s 1,s 2,s 3,…之比和在第1s ,第2s ,第3s ,…内的位移S Ⅰ,S Ⅱ,S Ⅲ,…之比各为多少?【一试身手】1.下列说法正确的是A .加速度增大,速度一定增大B .速度变化量Δv 越大,加速度就越大C .物体有加速度,速度就增加D .物体速度很大,加速度可能为零2. 关于速度和加速度的关系A .物体的速度为零时,加速度一定为零B .物体的加速度为零时,速度一定为零C .物体的速度改变时,加速度不一定改变D .物体的加速度方向改变时,速度方向不一定改变3.如图所示,Ⅰ、Ⅱ两条直线分别描述P 、Q 两个物体的s —t 图象,下列说法正确的是A .两物体均做匀速直线运动B .M 点表示两物体在时间t 内有相同的位移C .t 时间内P 的位移较小D .0~t ,P 比Q 的速度大,t 以后P 比Q 的速度小 4.某质点做匀变速直线运动,加速度的大小为2m/s 2,则在任意1s 内A .质点的末速度一定是初速度的2倍B .质点的末速度一定比初速度大2m/sC .质点的初速度可能比末速度大2m/sD .质点的速度大小一定改变了2m/s 5.做匀变速直线运动的质点,它在通过某一段位移中点位置的速度为v ,通过这段位移所用时间的中间时刻的速度为u ,则该质点A .做匀加速运动时,v <uB .做匀减速运动时,v <uC .做匀加速运动时,v >uD .做匀减速运动时,v >u6.一个质点做方向不变的直线运动,加速度的方向始终与速度的方向相同,但加速度的大小逐渐减小为零,在此过程中( )A .速度逐渐减小,当加速度减小到零时,速度达到最小值B .速度逐渐增大,当加速度减小到零时,速度达到最大值C .位移逐渐增大,当加速度减小到零时,位移将不再增大D .位移逐渐减小,当加速度减小到零时,位移达到最小值7.关于匀变速直线运动,下列说法中正确的是A 、加速度越大,物体的速度一定越大B 、加速度越小,物体的位移一定越小C 、物体在运动过程中的加速度保持不变D 、匀减速直线运动中,位移随时间的增加而减小8.质点做直线运动,当时间t = t 0时,位移S > 0,速度v > 0,加速度a > 0,此后加速度a 逐渐减小,则它的 ( )A .速度的变化越来越慢B .速度逐渐减小C .位移继续增大D .位移、速度始终为正值t st o M Ⅰ Ⅱ9.甲、乙、丙和丁是以时间为横轴的匀变速直线运动的图象,下面说法正确的是( )A .图甲是加速度—时间图象B .图乙是加速度—时间图象C .图丙是位移—时间图象D .图丁是速度—时间图象10.滑块以某一初速度冲上斜面做匀减速直线运动,到达斜面顶端时的速度为零.已知滑块通过斜面中点时的速度为v ,则滑块在前一半路程中的平均速度大小为A 、212 vB 、(2+1)vC 、2vD 、21v 11.一匀变速运动物体的位移随时间变化的函数关系是S=4t+t 2(m), 则它运动的初速度、加速度及2s末的速度分别是( )A . 0、 4m/s 2 、4m/sB . 4m/s 、 2m/s 2 、8m/sC . 4m/s 、1m/s 2 、8m/sD . 4m/s 、 2m/s 2 、6m/s12.一个物体做初速度为零的匀加速运动,该物体通过前一半位移和通过后一半位移所用的时间之比是( )A .2∶1B .2∶ 1C .(2+1)∶1D .(2-1)∶1二、填空题1.汽车以2m/s 2的加速度由静止开始启动,则第5s 末汽车的速度是_______m/s ,第5s 内汽车的平均速度是________m/s, 第5s 内汽车的位移是___________m 。
第六讲 位移与时间的关系-【初高中衔接】2021年新高一物理暑假精品课程(解析版)

第六讲位移与时间的关系知识点一、位移时间公式[提出问题]1.在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,如果把每一小段△t 内的运动看做匀速运动,则矩形面积之和等于各段匀速直线运动的位移。
如果把整个运动过程划分得非常非常细,当△t→0时,各矩形面积之和趋近于v-t 图线下面的面积,如图所示。
设初速度为v 0,加速度为a ,试通过V-t 图像推导其位移公式。
答案:方法一:用图形推导由前面的讨论可知,当时间间隔分割得足够小时,折线趋近于直线AP ,由此可以求出匀变速运动在时间t 内的位移,它在数值上等于直线AP 下方的梯形OAPQ 的面积(如图丙).这个面积等于21201122S S S OA OQ AR RP v t at =+=⨯+⨯=+,即位移2012x v t at =+这就是匀变速直线运动的位移公式.方法二:用公式推导由于位移x vt =,而02t v v v +=,又0t v v at =+,故002v v at x t ++=⨯,即2012x v t at =+.[要点提炼]1.匀变速直线运动的位移与时间的关系:x=v0t+12at22.当v0=0时,x=12at2(由静止开始的匀加速直线运动)3.当a=0时,x=v0t(匀速直线运动)4.公式中x、v0、a都是矢量,应用时必须选取统一的正方向.若选v0方向为正方向,则:物体加速,a取正值;物体减速,a取负值.若位移为正值,位移的方向与正方向相同;若位移为负值,位移的方向与正方向相反.5.公式x=v0t+12at2只适用于匀变速直线运动[经典例题]1.做匀加速直线运动的物体初速度是0.50m/s,加速度是20.10m/s,那么第4s末的瞬时速度4v=____,头4秒内的平均速度4v=____,4秒内通过的位移4s=___,第4秒内通过的位移IVs=____。
【答案】0.90m/s0.70m/s 2. 80 m0.85m【详解】[1]第4s末的瞬时速度为4040.90m/sv v at =+=[3][2]头4s 内的位移为240441 2.80m 2s v t at =+=则头4s 内的平均速度为4440.70m /s s v t ==[4]头3s 内的位移为230331 1.95m 2s v t at =+=则第4s 内通过的位移为2.一物体做初速度为零的匀加速直线运动,加速度为a =2m/s 2,求:(1)第5s 末物体的速度多大?(2)前4s 的位移多大?(3)第4s 内的位移多大?解析(1)第5s 末物体的速度由v t =v 0+at 1得v 1=0+2×5m/s =10m/s(2)前4s 的位移由x 1=v 0t +12at 2得x 1=0+12×2×42m =16m (3)物体第3s 末的速度v 2=v 0+at 2=0+2×3m/s =6m/s则第4s 内的位移x 2=v 2t 3+12at 23=6×1m +12×2×12m =7m 答案(1)10m/s (2)16m (3)7m3.做匀变速直线运动的物体,在一段时间t 内的平均速度等于这段时间内_____的瞬时速度,还等于这段时间初、末速度矢量和的一半。
第六讲 位移与时间的关系-【初高中衔接】2021年新高一物理暑假精品课程(原卷版)

第六讲位移与时间的关系知识点一、位移时间公式[提出问题]1.在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,如果把每一小段△t内的运动看做匀速运动,则矩形面积之和等于各段匀速直线运动的位移。
如果把整个运动过程划分得非常非常细,当△t→0时,各矩形面积之和趋近于v-t图线下面的面积,如图所示。
设初速度为v0,加速度为a,试通过V-t图像推导其位移公式。
[要点提炼]at21.匀变速直线运动的位移与时间的关系:x=v0t+12at2(由静止开始的匀加速直线运动)2.当v0=0时,x=123.当a=0时,x=(匀速直线运动)4.公式中x、v0、a都是矢量,应用时必须选取的正方向.若选v0方向为正方向,则:物体加速,a取值;物体减速,a取值.若位移为正值,位移的方向与正方向;若位移为负值,位移的方向与正方向at2只适用于5.公式x=v0t+12[经典例题]1.做匀加速直线运动的物体初速度是0.50m/s,加速度是20.10m/s,那么第4s末的瞬时速度4v=____,头4秒内的平均速度4v=____,4秒内通过的位移4s=___,第4秒内通过的位移IVs=____。
2.一物体做初速度为零的匀加速直线运动,加速度为a=2m/s2,求:(1)第5s末物体的速度多大?(2)前4s的位移多大?(3)第4s内的位移多大?3.做匀变速直线运动的物体,在一段时间t内的平均速度等于这段时间内_____的瞬时速度,还等于这段时间初、末速度矢量和的一半。
即022tt v vxv vt +===[变式训练]1.(2020·大石桥市)一列火车以2m/s的初速度,0.5m/s2的加速度做匀加速直线运动,求:(1)火车在第3s末的速度是多少?(2)火车在前4s内的位移是多少?(3)火车在第5s内的位移是多少?2.汽车在高速公路上行驶,起初以54km/h的速度前进10s,接着以20.6m/s的加速度匀加速前进15s。
匀变速直线运动的位移与时间的关系
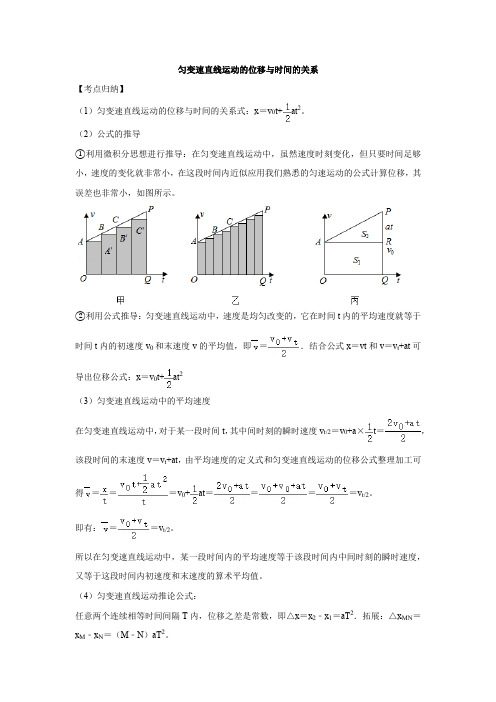
匀变速直线运动的位移与时间的关系【考点归纳】(1)匀变速直线运动的位移与时间的关系式:x=v0t+at2。
(2)公式的推导①利用微积分思想进行推导:在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,在这段时间内近似应用我们熟悉的匀速运动的公式计算位移,其误差也非常小,如图所示。
②利用公式推导:匀变速直线运动中,速度是均匀改变的,它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值,即=.结合公式x=vt和v=v t+at可导出位移公式:x=v0t+at2(3)匀变速直线运动中的平均速度在匀变速直线运动中,对于某一段时间t,其中间时刻的瞬时速度v t/2=v0+a×t=,该段时间的末速度v=v t+at,由平均速度的定义式和匀变速直线运动的位移公式整理加工可得===v0+at====v t/2。
即有:==v t/2。
所以在匀变速直线运动中,某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度,又等于这段时间内初速度和末速度的算术平均值。
(4)匀变速直线运动推论公式:任意两个连续相等时间间隔T内,位移之差是常数,即△x=x2﹣x1=aT2.拓展:△x MN=x M﹣x N=(M﹣N)aT2。
推导:如图所示,x1、x2为连续相等的时间T内的位移,加速度为a。
【命题方向】例1:对基本公式的理解汽车在平直的公路上以30m/s的速度行驶,当汽车遇到交通事故时就以7.5m/s2的加速度刹车,刹车2s内和6s内的位移之比()A.1:1B.5:9C.5:8D.3:4分析:求出汽车刹车到停止所需的时间,汽车刹车停止后不再运动,然后根据位移时间公式求出2s内和6s内的位移。
解:汽车刹车到停止所需的时间>2s所以刹车2s内的位移=45m。
t0<6s,所以刹车在6s内的位移等于在4s内的位移。
=60m。
所以刹车2s内和6s内的位移之比为3:4.故D正确,A、B、C错误。
高一物理匀变速直线运动的位移与时间关系

高一物理匀变速直线运动的位移与时间关系匀变速直线运动这玩意儿,听起来是不是有点高大上?简单说就是物体在一个固定的加速度下运动。
想象一下,一辆车从静止开始加速,哗啦啦地冲出去,感觉就像一只小鸟终于挣脱了笼子,飞向蓝天。
没错,这就是匀变速直线运动的魅力所在!我们来聊聊它的位移和时间之间的关系吧。
位移就是你从起点到终点走了多远。
比如,你从家里出发,去隔壁小卖部买冰淇淋,这个过程中的“走过的路”就是位移。
在匀变速直线运动中,时间越长,位移就越大,听起来是不是很简单?有个公式很重要,S=vt+1/2at²。
这里的S就是位移,v是初速度,t是时间,a是加速度。
要是你觉得这个公式复杂,不妨把它当成一块蛋糕,慢慢来,一口一口吃,总能消化得了。
想象一下你在操场上跑步,开始的时候慢吞吞的,但过了一会儿,你开始加速,仿佛自己是飞驰的箭。
这个过程的位移不是直线,而是弯弯曲曲的,但总体上来说,你跑得越久,位移就越大。
说到这里,有个小故事,听说有个小伙伴跑步比赛,刚开始他慢吞吞的,结果旁边的人都在嘲笑他,结果到他爆发式地加速,超越了所有人,真是“慢工出细活”,一口气追上,惊艳四座。
在匀变速直线运动中,时间和位移的关系可以形象地理解为一场追逐赛。
假如你是一只兔子,目标是一根胡萝卜,而加速度就是你跑的劲头,时间则是你追胡萝卜的过程。
随着时间的推移,你的位移不断增加,最终你抓到了胡萝卜,哦耶!这时你可能会感叹,原来时间和位移是如此紧密相连的。
就像“时间就是金钱”,在这里时间就是位移的好朋友。
再说说现实生活中,很多东西都遵循这个规律。
比如,开车的时候,油门一踩,车子就飞快地开出去。
起初你可能觉得慢吞吞,但一旦加速,瞬间就感觉到风在耳边呼啸,仿佛自己变成了赛车手。
而如果你有个小伙伴也在旁边开车,你们之间的距离会随着时间的增加而变化,这就是匀变速直线运动的真实体现。
大家可能会觉得匀变速直线运动有点无聊,但其实它在我们的生活中无处不在。
已知自由落体运动位移与时间关系的公式

自由落体运动是物理学中的一个经典问题,其位移与时间之间的关系经过长期的研究和实践验证,已经得到了精确的公式描述。
本文将对自由落体运动的位移与时间关系进行详细的探讨,让读者更好地理解这一经典物理问题。
一、自由落体运动的定义自由落体运动是指在只受重力作用下的物体的运动。
在这种情况下,物体的加速度恒定且指向重力方向,大小为重力加速度g。
自由落体运动是物理学中最基础的运动之一,也是许多物理问题的基础。
二、自由落体运动的位移与时间关系根据牛顿力学定律和运动学原理,自由落体运动的位移与时间之间的关系可以通过一个简单的公式来描述。
假设物体自由落体运动的初始速度为0,则物体在 t 秒内的下落距离可以用以下公式表示:s = (1/2)gt^2其中,s代表物体的位移,t代表时间,g代表重力加速度。
通过这个公式,可以清楚地看到自由落体运动的位移随时间的平方增加而增加。
这也符合我们在日常生活中对自由落体运动的观察,物体在下落的过程中位移是呈二次增加的。
三、自由落体实验验证为了验证自由落体运动的位移与时间关系公式的准确性,科学家们进行了大量的实验。
通过精密的测量和数据分析,实验结果与理论计算的值非常接近,验证了公式的准确性。
四、在物理学和工程中的应用自由落体运动的位移与时间关系公式在物理学和工程中有着广泛的应用。
在炮弹发射、天体运动、物体自由落体速度的计算等方面都可以通过这个公式来求解问题,为科学研究和工程设计提供了重要的理论基础。
结语自由落体运动的位移与时间关系公式是物理学中的一个基础而重要的问题,在认识和理解这个公式的基础上,不仅可以更好地学习物理学知识,还能够应用到实际的科学研究和工程设计中。
希望本文能够帮助读者更深入地了解自由落体运动的位移与时间关系,激发学习物理学的兴趣。
五、实际案例分析自由落体运动的位移与时间关系不仅在理论研究中有着重要的地位,在实际生活和工程应用中也有着广泛的应用。
在建筑工程中,设计者需要考虑物体自由落体运动的位移与时间关系,以确保建筑物和结构的安全性。
位移时间公式变形

位移时间公式变形位移时间公式是物理学中常见的一个公式,用于计算物体在给定加速度下的位移所需的时间。
它可以表示为:位移 = 1/2 * 加速度 * 时间的平方这个公式可以通过变形得到不同的表达方式,方便我们根据已知条件求解未知量。
下面将介绍几种常见的变形形式。
1. 时间的平方 = 2 * 位移 / 加速度这个变形形式可以通过已知位移和加速度来求解所需时间的平方。
将已知的位移和加速度代入公式中,通过计算得到时间的平方。
2. 时间 = 平方根(2 * 位移 / 加速度)这个变形形式是通过对上述公式求平方根得到的。
已知位移和加速度的值,可以通过计算得到所需的时间。
3. 加速度 = 2 * 位移 / 时间的平方这个变形形式是通过对原公式进行代数变换得到的。
已知位移和时间的值,可以通过计算得到加速度的大小。
4. 位移 = 加速度 * 时间的平方 / 2这个变形形式是通过对原公式进行代数变换得到的。
已知加速度和时间的值,可以通过计算得到位移的大小。
这些变形形式可以根据具体的问题来选择使用,以便更方便地求解所需的物理量。
例如,在计算自由落体运动中,我们可以根据已知的加速度和时间来求解位移,或者根据已知的位移和时间来求解加速度。
除了这些基本的变形形式,还可以根据具体问题进行更复杂的变形。
例如,在考虑空气阻力的情况下,位移时间公式需要进行修正,以考虑空气阻力对物体运动的影响。
位移时间公式的变形形式可以帮助我们根据已知条件求解未知量,从而更深入地理解物体在给定加速度下的运动规律。
在实际应用中,我们可以根据具体问题选择合适的变形形式来进行求解。
同时,我们也可以通过这些变形形式来推导出其他与位移、时间和加速度相关的公式,进一步扩展我们对物体运动规律的认识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
匀变速直线运动的位移与时间的关系教学反思
高中物理是一门重要的学科,但是对于刚刚步入高一物理学习的学生,对该学科往往望而却步,认为“物理难学”。
因此这就要求我们教师在教学过程中,认真总结和分析,对高一年级学生的物理教学,首先是要正确引导,其次要让学生建立一个良好的物理知识基础,然后根据学生的具体情况选择提高,教师应该多从自身的教学思想,以及对教材的把握上入手,有意识地降低高中物理学习的门槛,将学生引入物理世界的大门,这就要以对每一节教学过程进行及时的反思思考!以下是《匀变速直线运动的位移与时间的关系》一节的教学反思。
本节课的主体过程是引导同学们用极限思想得出v -t 图线下面四边形的面积代表匀变速直线运动的位移,导出位移公式x =v 0t +21at 2。
这种思想方法曾在上一章介绍瞬时速度和瞬时加速度的时候用到过,在这里又一次采用了这种极限的思想。
高中物理引入极限思想的出发点在于让学生了解这种常用的科学思维方法,而不苛求学生会计算极限。
这一点教师要好好把握。
教材课文从最简单的匀速直线运动的位移与时间的关系入手,得出位移公式x =vt 。
然后从匀速直线运动的速度—时间图象说明v -t 图线下面矩形的面积代表匀速直线运动的位移。
接着利用实验探究中所得到的一条纸带上时间与速度的记录,让学生思考与讨论如何求出小车的位移?进一步利用教材思考与讨论栏目提供的每隔0。
1 s 测得小车速度的数据,或学生自己在第一节实验中测得的数据,教师可让学生思考与讨论。
要鼓励学生积极思考,充分表达自己的想法。
学生会提出各种想法、问题,教师不要随便肯定或否定,可启发、引导学生具体、深入地分析,肯定学生正确的想法,弄清楚错误的原因。
教师可明确指出:Δt 越小,对位移的估算就越精确,这种想法看起来很烦琐,但能引导我们走上正确的道路,得到正确的结论。
教材详细分析了Δt 越小,位移估算的过程,可让学生阅读、议论。
教师明确总结:v -t 图线下四边形的面积等于匀加速直线运动的小车的位移。
由此导出位移公式x =v 0t +21at 2。
教材在处理得出位移公式的过程方法上与以往有很大的不同。
以往的做法是:通过匀变速直线运动的速度是均匀改变的,它在时间t 内的平均速度v ,就等于时间t 内的初速度v 0和末速度v 的平均值,即v =
2
0v v ,把它代入x =v t 中,
得到x =v t =20v v t ,其中v =v 0+at ,代入后得到x =v 0t +2
1at 2。
尽管这种方式也是一种处理方法,但是物理思想和科学思维方法等方面的教育价值不同。
老师们要充分挖掘发挥教材改革的这一思想,不要回到原来的老教法、老路子上去。
教材在得出位移公式后,紧接着以一典型的实例来训练这一公式的应用。
注意在例题教学过程中要充分发挥学生的主体参与意识,让学生自己审题,用自己的语言讲清楚题目所描述的物理过程,用形象化的物理过程示意图来展示自己读题后所获取的信息,使题目所描述的物理情景在头脑中更加清晰、明确。
切忌草草读题后乱套公式。
例题后还告诉学生一种方法,就是解题过程中一般应先用字母代表物理量进行运算,得出用已知量表达未知量的关系式,然后再把数值代入公式中,求出未知量。
这种做法能够清楚地看出未知量与已知量的关系,计算也比较简便。
教材在处理匀变速直线运动的位移与速度的关系时,直接以实例的形式呈现。
讲述子弹在枪筒内加速的过程,让学生在解决这个实际问题的过程中得出位移与时间的关系式。
可以组织学生先进行讨论,再让学生画出子弹的运动过程示意图,引导学生导出v 2=2ax ,然后在此基础上,再让学生导出初速度不为零的位移与速度关系式v 2-v 02=2ax 。
使用匀变速直线运动的规律解决问题时,应注意让学生理解规律的适用范围,养成认真审题、理解题意进而求解的习惯。
教学中教师要特别强调分析清楚物理过程,这样才能正确地应用公式,并对问题的结果进行必要的检验、讨论。
并注意引导同学分析已知、未知,画运动过程示意图的习惯。
