高考真题空间几何体
专题37 空间几何体(知识梳理)(新高考地区专用)(解析版)

专题37 空间几何体(知识梳理)一、空间几何体1、空间几何体的基本定义如果只考虑一个物体占有空间部分的形状和大小,而不考虑其它因素,则这个空间部分就是一个几何体。
围成体的各个平面图形叫做体的面;相邻两个面的公共边叫做体的棱;棱和棱的公共点叫做体的顶点。
几何体不是实实在在的物体。
平面的特性:无限延展、处处平直、没有其他性质(如厚度、大小、面积、体积、重量等)。
例1-1.下列是几何体的是( )。
A 、方砖B 、足球C 、圆锥D 、魔方【答案】C【解析】几何体不是实实在在的物体,故选C 。
例1-2.判断下列说法是否正确:(1)平静的湖面是一个平面。
(×)(2)一个平面长3cm ,宽4cm 。
(×)(3)三个平面重叠在一起,比一个平面厚。
(×)(4)书桌面是平面。
(×)(5)通过改变直线的位置,可以把直线放在某个平面内。
(√)【解析】平面可以看成是直线平行移动形成的,所以直线通过改变其位置,可以放在某个平面内。
(6)平行四边形是一个平面。
(×)(7)长方体是由六个平面围成的几何体。
(×)(8)任何一个平面图形都是一个平面。
(×)(9)长方体一个面上任一点到对面的距离相等。
(√)(10)空间图形中先画的线是实线,后画的线是虚线。
(×)(11)平面是绝对平的,无厚度,可以无限延展的抽象的数学概念。
(√) 例1-3.下列说法正确的是 。
①长方体是由六个平面围成的几何体;②长方体可以看作一个矩形ABCD 上各点沿铅垂线向上移动相同距离到矩形D C B A ''''所围成的几何体;③长方体一个面上的任一点到对面的距离相等。
【答案】②③【解析】①错,因长方体由6个矩形(包括它的内部)围成,注意“平面”与“矩形”的本质区别;②正确;③正确。
[多选]例1-4.下列说法正确的是( )。
A 、任何一个几何体都必须有顶点、棱和面B 、一个几何体可以没有顶点C 、一个几何体可以没有棱D 、一个几何体可以没有面【答案】BC【解析】球只有一个曲面围成,故A 错、B 对、C 对,由于几何体是空间图形,故一定有面,D 错,故选BC 。
专题14 空间几何体的结构、面积与体积(练)【解析版】

第一篇热点、难点突破篇专题14空间几何体的结构、面积与体积(练)【对点演练】一、单选题1.(2022秋·北京·高三统考阶段练习)已知圆柱的上、下底面的中心分别为1O,2O,过直O O的平面截该圆柱所得的截面是面积为12的正方形,则该圆柱的体积为()线12A.B.12πC.D.则该圆台的体积为()A.36πB.40πC.42πD.45πOO的长度===,1O为ABC的外接圆的圆心,球O的表面积为64π,则1AB BC AC为()B.2C.D.3A【答案】C【分析】由已知求得球O的半径4r=,即可求R=,根据正弦定理求出ABC外接圆半径2出结果.O的半径为r,球O的半径为R.【详解】设圆1依题意得ABC 为等边三角形,则由正弦定理得O 的表面积为如图,根据球的截面性质得2d OA ==的扇形,则该圆锥的侧面积为( ) A .π B .3π2C D .点作球O 的截面,则最小截面的面积为( ) A .3π B .4πC .5πD .6π子,其形状可以看成一个正四面体.广东流行粽子里放蛋黄,现需要在四角状粽子内部放入一个蛋黄,蛋黄的形状近似地看成球,当这个蛋黄的表面积是9π时,则该正四面体的高的最小值为()A.4B.6C.8D.10实物图,石碾子主要由碾盘、碾滚(圆柱形)和碾架组成.碾盘中心设竖轴(碾柱),连碾架,架中装碾滚,以人推或畜拉的方式,通过碾滚在碾盘上的滚动达到碾轧加工粮食作物的目的.若推动拉杆绕碾盘转动2周,碾滚的外边缘恰好滚动了5圈,碾滚与碾柱间的距离忽略不计,则该圆柱形碾滚的高与其底面圆的直径之比约为()A.3:2B.5:4C.5:3D.4:3一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.若一个直角圆锥的侧面积为,则该圆锥的体积为( )A .B .C .D .9π中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为h (轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O ,半径r 为的球,其上点A 的纬度是指OA 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为α,记卫星信号覆盖地球表面的表面积为22(1cos )S r πα=-(单位:2km ),若458h r =,则S 占地球表面积的百分比约为( ) A .26% B .34% C .42% D .50%【答案】C【分析】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,得AOC α∠=,在直角三角形中求出cos α后,可计算两者面积比.【详解】设C 表示卫星,过CO 作截面,截地球得大圆O ,过C 作圆O 的切线,CA CB ,线段CO 交圆O 于E ,如图,则AOC α∠=,r OE =,CE h =,OA CA ⊥,二、填空题10.(2022秋·江苏徐州·高三期末)已知圆柱的高为8,该圆柱内能容纳半径最大的球的表面积为36π,则圆柱的体积为______.【答案】72π【分析】先分析半径最大的球不可能为圆柱的内切球,所以此球是与圆柱侧面与下底面相切的球,就能求出圆柱底面半径,然后根据圆柱的体积公式可得.【详解】圆柱内能容纳半径最大的球的表面积为36π,设此球半径为r,则24π36π3r r=⇒=如果圆柱有内切球,又因为圆柱的高为8,所以内切球半径为43>,说明这个圆柱内能容纳半径最大的球,与圆柱侧面和下底面相切,与上底面相离,易得圆柱底面半径为3,圆柱的体积为2π3872π⋅⨯=故答案为:72π【冲刺提升】一、单选题1.(2022秋·广东东莞·高三统考期末)已知一个装满水的圆台形容器的上底半径为6,下底半径为1,高为,若将一个铁球放入该容器中,使得铁球完全没入水中,则可放入的铁球的体积的最大值为()A.B.C D.108π【答案】B【分析】作出体积最大时的剖面图,分析出此时圆与上底,两腰相切,建立合适直角坐标系,()53,05<<t=-533)32332=模拟预测)某工厂要生产容积为为侧面成本的2倍,为使成本最小,则圆柱的高与底面半径之比应为()A.1B.1C.2D.4 2圆柱上下底的总面积为3.(2022·浙江·模拟预测)如图,正方体1111的棱长为1,,E F 分别为棱BC ,11的中点,则三棱锥1B AEF -的体积为( )A .524B .316C .29D .181AB ES =因为正方体ABCD A B C D -的棱长为1, 所以111(,1,0),(0,1,1),(1,22AE AB AF =-==-的法向量为(,,)n x y z =112n AE x n AB y z ⎧⋅=-⎪⎨⎪⋅=+⎩所以(2,1,1)n =-,F 平面1AB E 的距离为2AF n n-+⋅=又因为1AB =,121122AB EAB S⎫==⋅⎪⎭所以三棱锥故选:AF ,G ,H 分别是SA ,SB ,BC ,AC 的中点,则四边形EFGH 面积的取值范围是( ) A .()0,∞+ B .⎫∞⎪⎪⎝⎭ C .⎫+∞⎪⎪⎝⎭D .1,2⎛⎫+∞ ⎪⎝⎭【答案】B【分析】画出图形,求出,EF HG ,说明EFHG 是矩形,结合图形,说明S 点在ABC 平面时,面积最小,求出即可得到范围 【详解】如图所示:由正三棱锥S ABC -的底面边长是2,因为E 、F 、G 、H 分别是SA 、SB 、BC 、AC 的中点,设ABC 的中心为SC OA >=所以EFGH 所以四边形且4BC =,6BD =,面ABC 与面BCD 夹角正弦值为1,则空间四边形ABCD 外接球与内切球的表面积之比为( )A B C D 【答案】C【分析】根据空间四边形ABCD 的线面关系可得DB ⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱中,根据圆柱的外接球半径求得空间四边形ABCD 的外接球半径R ,又根据内切球的几何性质用等体积法可求得空间四边形ABCD 的内切球半径r ,即可得空间四边形ABCD 外接球与内切球的表面积之比.【详解】解:面ABC 与面BCD 夹角正弦值为1,∴面ABC ⊥面BCD ,又面ABC ⋂面BCD BC =,DB BC DB ⊥⊂面BCD ,DB ∴⊥平面ABC ,则空间四边形ABCD 可以内接于圆柱12O O 中,如下图所示:点在上底面圆周上,ABC三个顶点在下底面圆周上,则圆柱O O的外接球即空间四边连接OA,则球心为为正ABC4sin6032BC=︒1111333ABC ABD ADC BCDS r S r S r S r⋅+⋅+⋅+⋅,,所以()22142132832ADCS=⨯⨯-=,44612ABC ABD ADC BCDS S S S⨯⨯⨯=+++⨯外接球与内切球的表面积之比为6.(2022秋·湖南长沙·高三长郡中学校考阶段练习)三棱锥A BCD -中,AB BC AD CD BD AC ======,则三棱锥A BCD -的外接球的表面积为( )A .20πB .28πC .32πD .36π23AB AD ==且E 为BD 中点,AE BD ∴⊥,AE AB ∴=又AE CE =120, 过BCD △的外心作平面同理过ABD △l l O ''=,易知连接O E ',O 为BCD △又在OO E '中,603=,∴得27O C O O ''=,即外接球半径7=,故外接球表面积28π=.故选:B7.(2022秋·天津河东·高三统考期末)一个球与一个正三棱柱(底面为等边三角形,侧棱与底面垂直)的两个底面和三个侧面都相切,若棱柱的体积为)A.16πB.4πC.8πD.32π8.(2022秋·黑龙江牡丹江·高三牡丹江一中校考期末)如图截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点所产生的多面体.如图,将棱长为3的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为1的截角四面体.则该截角四面体的表面积是______.正六边形每个内角均为2π111A B C 中,点P 在棱1BB 上,且1PA PC ⊥,当1APC 的面积取最小值时,三棱锥-P ABC 的外接球的表面积为______.【答案】28π时,1APC 面积取得最小值,补形后三棱锥的外接球,求出外接球半径和表面积【详解】由勾股定理得:AB =,则16PA =(7x y ++1APC S =2169y +,即2x =其中长方体的外接球的直径为,平面PAB ⊥平面PCD ,则P ABCD -体积的最大值为__________.PO ⊥平面ABCD ,PE CD⊥CD平面POE∴⊥,CD OE底面ABCD是边长为∴⊥,CD BCOE⊂平面ABCD OE BC∴,同理可得:OF∥O E F三点共线故,,∥,且有EF BC设平面PAB⋂平面∥AB CD AB,∴∥∥l AB⊥PE CD平面PAB∴⊥平面PEPF⊂平面∴⊥PE PF不妨设PE22∴+x y且2OP=-即2y m11.(2023·广西梧州·统考一模)边长为1的正方形ABCD 中,点M ,N 分别是DC ,BC 的中点,现将ABN ,ADM △分别沿AN ,AM 折起,使得B ,D 两点重合于点P ,连接PC ,得到四棱锥P AMCN -.(1)证明:平面APN ⊥平面PMN ;(2)求四棱锥P AMCN -的体积. ,所以PMN 为直角三角形,即PMN S=111111222AMN ABN ADM CMN ABCD S S S S S =---=-⨯⨯⨯-⨯正方形设点P 到平面AMN 的距离为h ,由A PMN P V V --=1133PMN AMN S PA S h ⋅=⋅△△,即13188h ⨯=,得h =)AMN MCN S S h +=AMCN 的体积为全国·高三对口高考)如题图,是圆锥底面的圆心,ABC 是底面的内接正三角形.P 为DO 上一点,90APC ∠=︒.(1)求证:PC ⊥平面PAB ;(2)若DO =.求三棱锥-P ABC 的体积. 因为ABC 是底面的内接正三角形,CO AB ⊥,PO OC ⋂AB ⊥平面PC ⊂平面AB PC ⊥,PA AB A =,⊥平面PAB(2)解:设圆锥的母线为l,底面半径为r,则圆锥的侧面积为ππ,即,=603所以,在等腰直角三角形APC。
高考数学空间几何高考真题
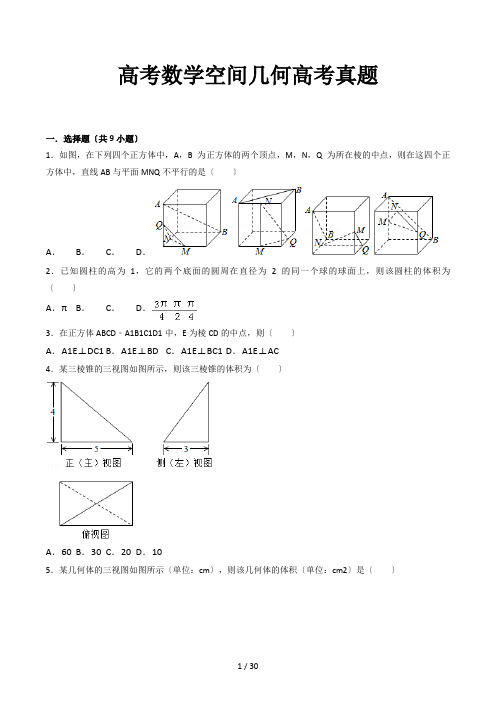
高考数学空间几何高考真题一.选择题〔共9小题〕1.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是〔〕A.B.C.D.2.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为〔〕A.πB.C.D.3.在正方体ABCD﹣A1B1C1D1中,E为棱CD的中点,则〔〕A.A1E⊥DC1 B.A1E⊥BD C.A1E⊥BC1 D.A1E⊥AC4.某三棱锥的三视图如图所示,则该三棱锥的体积为〔〕A.60 B.30 C.20 D.105.某几何体的三视图如图所示〔单位:cm〕,则该几何体的体积〔单位:cm2〕是〔〕A.+1 B.+3 C.+1 D.+36.如图,已知正四面体D﹣ABC〔所有棱长均相等的三棱锥〕,P、Q、R分别为AB、BC、CA上的点,AP=PB,==2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则〔〕A.γ<α<βB.α<γ<βC.α<β<γD.β<γ<α7.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为〔〕A.90πB.63πC.42πD.36π1.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为〔〕A.10 B.12 C.14 D.162.已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为〔〕A.B.C.D.二.填空题〔共5小题〕8.已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S﹣ABC的体积为9,则球O的表面积为.9.长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为.10.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为.11.由一个长方体和两个圆柱体构成的几何体的三视图如图,则该几何体的体积为.12.如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则的值是.三.解答题〔共9小题〕13.如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.〔1〕证明:平面PAB⊥平面PAD;〔2〕若PA=PD=AB=DC,∠APD=90°,且四棱锥P﹣ABCD的体积为,求该四棱锥的侧面积.14.如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.〔1〕证明:直线BC∥平面PAD;〔2〕若△PCD面积为2,求四棱锥P﹣ABCD的体积.15.如图四面体ABCD中,△ABC是正三角形,AD=CD.〔1〕证明:AC⊥BD;〔2〕已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.16.如图,直三棱柱ABC﹣A1B1C1的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱AA1的长为5.〔1〕求三棱柱ABC﹣A1B1C1的体积;〔2〕设M是BC中点,求直线A1M与平面ABC所成角的大小.17.如图,在三棱锥P﹣ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.〔1〕求证:PA⊥BD;〔2〕求证:平面BDE⊥平面PAC;〔3〕当PA∥平面BDE时,求三棱锥E﹣BCD的体积.18.如图,在四棱锥P﹣ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.〔Ⅰ〕求异面直线AP与BC所成角的余弦值;〔Ⅱ〕求证:PD⊥平面PBC;〔Ⅲ〕求直线AB与平面PBC所成角的正弦值.19.如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.〔Ⅰ〕证明:CE∥平面PAB;〔Ⅱ〕求直线CE与平面PBC所成角的正弦值.20.由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,〔Ⅰ〕证明:A1O∥平面B1CD1;〔Ⅱ〕设M是OD的中点,证明:平面A1EM⊥平面B1CD1.21.如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F〔E与A、D不重合〕分别在棱AD,BD上,且EF⊥AD.求证:〔1〕EF∥平面ABC;〔2〕AD⊥AC.3.如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.〔1〕证明:平面PAB⊥平面PAD;〔2〕若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.4.如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°,E是PD的中点.〔1〕证明:直线CE∥平面PAB;〔2〕点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.5.如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.〔1〕证明:平面ACD⊥平面ABC;〔2〕过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C 的余弦值.6.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.〔1〕求证:M为PB的中点;〔2〕求二面角B﹣PD﹣A的大小;〔3〕求直线MC与平面BDP所成角的正弦值.7.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.〔Ⅰ〕求证:MN∥平面BDE;〔Ⅱ〕求二面角C﹣EM﹣N的正弦值;〔Ⅲ〕已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线段AH的长.8.如图,几何体是圆柱的一部分,它是由矩形ABCD〔及其内部〕以AB边所在直线为旋转轴旋转120°得到的,G是的中点.〔Ⅰ〕设P是上的一点,且AP⊥BE,求∠CBP的大小;〔Ⅱ〕当AB=3,AD=2时,求二面角E﹣AG﹣C的大小.2017年高考数学空间几何高考真题参考答案与试题解析一.选择题〔共7小题〕1.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是〔〕A.B.C.D.【解答】解:对于选项B,由于AB∥MQ,结合线面平行判定定理可知B不满足题意;对于选项C,由于AB∥MQ,结合线面平行判定定理可知C不满足题意;对于选项D,由于AB∥NQ,结合线面平行判定定理可知D不满足题意;所以选项A满足题意,故选:A.2.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为〔〕A.πB.C.D.【解答】解:∵圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,∴该圆柱底面圆周半径r==,∴该圆柱的体积:V=Sh==.故选:B.3.在正方体ABCD﹣A1B1C1D1中,E为棱CD的中点,则〔〕A.A1E⊥DC1 B.A1E⊥BD C.A1E⊥BC1 D.A1E⊥AC【解答】解:法一:连B1C,由题意得BC1⊥B1C,∵A1B1⊥平面B1BCC1,且BC1⊂平面B1BCC1,∴A1B1⊥BC1,∵A1B1∩B1C=B1,∴BC1⊥平面A1ECB1,∵A1E⊂平面A1ECB1,∴A1E⊥BC1.故选:C.法二:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1中棱长为2,则A1〔2,0,2〕,E〔0,1,0〕,B〔2,2,0〕,D〔0,0,0〕,C1〔0,2,2〕,A〔2,0,0〕,C 〔0,2,0〕,=〔﹣2,1,﹣2〕,=〔0,2,2〕,=〔﹣2,﹣2,0〕,=〔﹣2,0,2〕,=〔﹣2,2,0〕,∵•=﹣2,=2,=0,=6,∴A1E⊥BC1.故选:C.4.某三棱锥的三视图如图所示,则该三棱锥的体积为〔〕A.60 B.30 C.20 D.10【解答】解:由三视图可知:该几何体为三棱锥,该三棱锥的体积==10.故选:D.5.某几何体的三视图如图所示〔单位:cm〕,则该几何体的体积〔单位:cm2〕是〔〕A.+1 B.+3 C.+1 D.+3【解答】解:由几何的三视图可知,该几何体是圆锥的一半和一个三棱锥组成,圆锥的底面圆的半径为1,三棱锥的底面是底边长2的等腰直角三角形,圆锥的高和棱锥的高相等均为3,故该几何体的体积为××π×12×3+××××3=+1,故选:A6.如图,已知正四面体D﹣ABC〔所有棱长均相等的三棱锥〕,P、Q、R分别为AB、BC、CA上的点,AP=PB,==2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则〔〕A.γ<α<βB.α<γ<βC.α<β<γD.β<γ<α【解答】解法一:如图所示,建立空间直角坐标系.设底面△ABC的中心为O.不妨设OP=3.则O〔0,0,0〕,P〔0,﹣3,0〕,C〔0,﹣6,0〕,D〔0,0,6〕,Q,R,=,=〔0,3,6〕,=〔,5,0〕,=,=.设平面PDR的法向量为=〔x,y,z〕,则,可得,可得=,取平面ABC的法向量=〔0,0,1〕.则cos==,取α=arccos.同理可得:β=arccos.γ=arccos.∵>>.∴α<γ<β.解法二:如图所示,连接OP,OQ,OR,过点O分别作垂线:OE⊥PR,OF⊥PQ,OG⊥QR,垂足分别为E,F,G,连接DE,DF,DG.设OD=h.则tanα=.同理可得:tanβ=,tanγ=.由已知可得:OE>OG>OF.∴tanα<tanγ<tanβ,α,β,γ为锐角.∴α<γ<β.故选:B.7.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为〔〕A.90πB.63πC.42πD.36π【解答】解:由三视图可得,直观图为一个完整的圆柱减去一个高为6的圆柱的一半,V=π•32×10﹣•π•32×6=63π,故选:B.1.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为〔〕A.10 B.12 C.14 D.16【解答】解:由三视图可画出直观图,该立体图中只有两个相同的梯形的面,S梯形=×2×〔2+4〕=6,∴这些梯形的面积之和为6×2=12,故选:B2.已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为〔〕A.B.C.D.【解答】解:【解法一】如图所示,设M、N、P分别为AB,BB1和B1C1的中点,则AB1、BC1夹角为MN和NP夹角或其补角〔因异面直线所成角为〔0,]〕,可知MN=AB1=,NP=BC1=;作BC中点Q,则△PQM为直角三角形;∵PQ=1,MQ=AC,△ABC中,由余弦定理得AC2=AB2+BC2﹣2AB•BC•cos∠ABC=4+1﹣2×2×1×〔﹣〕=7,∴AC=,∴MQ=;在△MQP中,MP==;在△PMN中,由余弦定理得cos∠MNP===﹣;又异面直线所成角的范围是〔0,],∴AB1与BC1所成角的余弦值为.【解法二】如图所示,补成四棱柱ABCD﹣A1B1C1D1,求∠BC1D即可;BC1=,BD==,C1D=,∴+BD2=,∴∠DBC1=90°,∴cos∠BC1D==.二.填空题〔共5小题〕8.已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S﹣ABC的体积为9,则球O的表面积为36π.【解答】解:三棱锥S﹣ABC的所有顶点都在球O的球面上,SC是球O的直径,若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S﹣ABC的体积为9,可知三角形SBC与三角形SAC都是等腰直角三角形,设球的半径为r,可得,解得r=3.球O的表面积为:4πr2=36π.故答案为:36π.9.长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为14π.【解答】解:长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,可知长方体的对角线的长就是球的直径,所以球的半径为:=.则球O的表面积为:4×=14π.故答案为:14π.10.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为.【解答】解:设正方体的棱长为a,∵这个正方体的表面积为18,∴6a2=18,则a2=3,即a=,∵一个正方体的所有顶点在一个球面上,∴正方体的体对角线等于球的直径,即a=2R,即R=,则球的体积V=π•〔〕3=;故答案为:.11.由一个长方体和两个圆柱体构成的几何体的三视图如图,则该几何体的体积为2+.【解答】解:由长方体长为2,宽为1,高为1,则长方体的体积V1=2×1×1=2,圆柱的底面半径为1,高为1,则圆柱的体积V2=×π×12×1=,则该几何体的体积V=V1+2V1=2+,故答案为:2+.12.如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则的值是.【解答】解:设球的半径为R,则球的体积为:R3,圆柱的体积为:πR2•2R=2πR3.则==.故答案为:.三.解答题〔共9小题〕13.如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.〔1〕证明:平面PAB⊥平面PAD;〔2〕若PA=PD=AB=DC,∠APD=90°,且四棱锥P﹣ABCD的体积为,求该四棱锥的侧面积.【解答】证明:〔1〕∵在四棱锥P﹣ABCD中,∠BAP=∠CDP=90°,∴AB⊥PA,CD⊥PD,又AB∥CD,∴AB⊥PD,∵PA∩PD=P,∴AB⊥平面PAD,∵AB⊂平面PAB,∴平面PAB⊥平面PAD.解:〔2〕设PA=PD=AB=DC=a,取AD中点O,连结PO,∵PA=PD=AB=DC,∠APD=90°,平面PAB⊥平面PAD,∴PO⊥底面ABCD,且AD==,PO=,∵四棱锥P﹣ABCD的体积为,∴VP﹣ABCD=====,解得a=2,∴PA=PD=AB=DC=2,AD=BC=2,PO=,∴PB=PC==2,∴该四棱锥的侧面积:S侧=S△PAD+S△PAB+S△PDC+S△PBC=+++==6+2.14.如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.〔1〕证明:直线BC∥平面PAD;〔2〕若△PCD面积为2,求四棱锥P﹣ABCD的体积.【解答】〔1〕证明:四棱锥P﹣ABCD中,∵∠BAD=∠ABC=90°.∴BC∥AD,∵AD⊂平面PAD,BC⊄平面PAD,∴直线BC∥平面PAD;〔2〕解:四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.设AD=2x,则AB=BC=x,CD=,O是AD的中点,连接PO,OC,CD的中点为:E,连接OE,则OE=,PO=,PE==,△PCD面积为2,可得:=2,即:,解得x=2,PE=2.则V P﹣ABCD=×〔BC+AD〕×AB×PO==4.15.如图四面体ABCD中,△ABC是正三角形,AD=CD.〔1〕证明:AC⊥BD;〔2〕已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.【解答】证明:〔1〕取AC中点O,连结DO、BO,∵△ABC是正三角形,AD=CD,∴DO⊥AC,BO⊥AC,∵DO∩BO=O,∴AC⊥平面BDO,∵BD⊂平面BDO,∴AC⊥BD.解:〔2〕法一:连结OE,由〔1〕知AC⊥平面OBD,∵OE⊂平面OBD,∴OE⊥AC,设AD=CD=,则OC=OA=1,∴E是线段AC垂直平分线上的点,∴EC=EA=CD=,由余弦定理得:cos∠CBD==,即,解得BE=1或BE=2,∵BE<<BD=2,∴BE=1,∴BE=ED,∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,∵BE=ED,∴S△DCE=S△BCE,∴四面体ABCE与四面体ACDE的体积比为1.法二:设AD=CD=,则AC=AB=BC=BD=2,AO=CO=DO=1,∴BO==,∴BO2+DO2=BD2,∴BO⊥DO,以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,则C〔﹣1,0,0〕,D〔0,0,1〕,B〔0,,0〕,A〔1,0,0〕,设E〔a,b,c〕,,〔0≤λ≤1〕,则〔a,b,c﹣1〕=λ〔0,,﹣1〕,解得E〔0,,1﹣λ〕,∴=〔1,〕,=〔﹣1,〕,∵AE⊥EC,∴=﹣1+3λ2+〔1﹣λ〕2=0,由λ∈[0,1],解得,∴DE=BE,∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,∵DE=BE,∴S△DCE=S△BCE,∴四面体ABCE与四面体ACDE的体积比为1.16.如图,直三棱柱ABC﹣A1B1C1的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱AA1的长为5.〔1〕求三棱柱ABC﹣A1B1C1的体积;〔2〕设M是BC中点,求直线A1M与平面ABC所成角的大小.【解答】解:〔1〕∵直三棱柱ABC﹣A1B1C1的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱AA1的长为5.∴三棱柱ABC﹣A1B1C1的体积:V=S△ABC×AA1===20.〔2〕连结AM,∵直三棱柱ABC﹣A1B1C1的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱AA1的长为5,M是BC中点,∴AA1⊥底面ABC,AM==,∴∠A1MA是直线A1M与平面ABC所成角,tan∠A1MA===,∴直线A1M与平面ABC所成角的大小为arctan.17.如图,在三棱锥P﹣ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.〔1〕求证:PA⊥BD;〔2〕求证:平面BDE⊥平面PAC;〔3〕当PA∥平面BDE时,求三棱锥E﹣BCD的体积.【解答】解:〔1〕证明:由PA⊥AB,PA⊥BC,AB⊂平面ABC,BC⊂平面ABC,且AB∩BC=B,可得PA⊥平面ABC,由BD⊂平面ABC,可得PA⊥BD;〔2〕证明:由AB=BC,D为线段AC的中点,可得BD⊥AC,由PA⊥平面ABC,PA⊂平面PAC,可得平面PAC⊥平面ABC,又平面ABC∩平面ABC=AC,BD⊂平面ABC,且BD⊥AC,即有BD⊥平面PAC,BD⊂平面BDE,可得平面BDE⊥平面PAC;〔3〕PA∥平面BDE,PA⊂平面PAC,且平面PAC∩平面BDE=DE,可得PA∥DE,又D为AC的中点,可得E为PC的中点,且DE=PA=1,由PA⊥平面ABC,可得DE⊥平面ABC,可得S△BDC=S△ABC=××2×2=1,则三棱锥E﹣BCD的体积为DE•S△BDC=×1×1=.18.如图,在四棱锥P﹣ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.〔Ⅰ〕求异面直线AP与BC所成角的余弦值;〔Ⅱ〕求证:PD⊥平面PBC;〔Ⅲ〕求直线AB与平面PBC所成角的正弦值.【解答】解:〔Ⅰ〕如图,由已知AD∥BC,故∠DAP或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得,故.所以,异面直线AP与BC所成角的余弦值为.证明:〔Ⅱ〕因为AD⊥平面PDC,直线PD⊂平面PDC,所以AD⊥PD.又因为BC∥AD,所以PD⊥BC,又PD⊥PB,所以PD⊥平面PBC.解:〔Ⅲ〕过点D作AB的平行线交BC于点F,连结PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,所以∠DFP为直线DF和平面PBC所成的角.由于AD∥BC,DF∥AB,故BF=AD=1,由已知,得CF=BC﹣BF=2.又AD⊥DC,故BC⊥DC,在Rt△DCF中,可得.所以,直线AB与平面PBC所成角的正弦值为.19.如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.〔Ⅰ〕证明:CE∥平面PAB;〔Ⅱ〕求直线CE与平面PBC所成角的正弦值.【解答】证明:〔Ⅰ〕取AD的中点F,连结EF,CF,∵E为PD的中点,∴EF∥PA,在四边形ABCD中,BC∥AD,AD=2DC=2CB,F为中点,∴CF∥AB,∴平面EFC∥平面ABP,∵EC⊂平面EFC,∴EC∥平面PAB.解:〔Ⅱ〕连结BF,过F作FM⊥PB于M,连结PF,∵PA=PD,∴PF⊥AD,推导出四边形BCDF为矩形,∴BF⊥AD,∴AD⊥平面PBF,又AD∥BC,∴BC⊥平面PBF,∴BC⊥PB,设DC=CB=1,则AD=PC=2,∴PB=,BF=PF=1,∴MF=,又BC⊥平面PBF,∴BC⊥MF,∴MF⊥平面PBC,即点F到平面PBC的距离为,∵MF=,D到平面PBC的距离应该和MF平行且相等,为,E为PD中点,E到平面PBC的垂足也为垂足所在线段的中点,即中位线,∴E到平面PBC的距离为,在,由余弦定理得CE=,设直线CE与平面PBC所成角为θ,则sinθ==.20.由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,〔Ⅰ〕证明:A1O∥平面B1CD1;〔Ⅱ〕设M是OD的中点,证明:平面A1EM⊥平面B1CD1.【解答】证明:〔Ⅰ〕取B1D1中点G,连结A1G、CG,∵四边形ABCD为正方形,O为AC与BD 的交点,∴四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后,A1GOC,∴四边形OCGA1是平行四边形,∴A1O∥CG,∵A1O⊄平面B1CD1,CG⊂平面B1CD1,∴A1O∥平面B1CD1.〔Ⅱ〕四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后,BDB1D1,∵M是OD的中点,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,又BD⊂平面ABCD,∴BD⊥A1E,∵四边形ABCD为正方形,O为AC与BD 的交点,∴AO⊥BD,∵M是OD的中点,E为AD的中点,∴EM⊥BD,∵A1E∩EM=E,∴BD⊥平面A1EM,∵BD∥B1D1,∴B1D1⊥平面A1EM,∵B1D1⊂平面B1CD1,∴平面A1EM⊥平面B1CD1.21.如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F〔E与A、D不重合〕分别在棱AD,BD上,且EF⊥AD.求证:〔1〕EF∥平面ABC;〔2〕AD⊥AC.【解答】证明:〔1〕因为AB⊥AD,EF⊥AD,且A、B、E、F四点共面,所以AB∥EF,又因为EF⊊平面ABC,AB⊆平面ABC,所以由线面平行判定定理可知:EF∥平面ABC;〔2〕在线段CD上取点G,连结FG、EG使得FG∥BC,则EG∥AC,因为BC⊥BD,FG∥BC,所以FG⊥BD,又因为平面ABD⊥平面BCD,所以FG⊥平面ABD,所以FG⊥AD,又因为AD⊥EF,且EF∩FG=F,所以AD⊥平面EFG,所以AD⊥EG,故AD⊥AC.3.如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.〔1〕证明:平面PAB⊥平面PAD;〔2〕若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.【解答】〔1〕证明:∵∠BAP=∠CDP=90°,∴PA⊥AB,PD⊥CD,∵AB∥CD,∴AB⊥PD,又∵PA∩PD=P,且PA⊂平面PAD,PD⊂平面PAD,∴AB⊥平面PAD,又AB⊂平面PAB,∴平面PAB⊥平面PAD;〔2〕解:∵AB∥CD,AB=CD,∴四边形ABCD为平行四边形,由〔1〕知AB⊥平面PAD,∴AB⊥AD,则四边形ABCD为矩形,在△APD中,由PA=PD,∠APD=90°,可得△PAD为等腰直角三角形,设PA=AB=2a,则AD=.取AD中点O,BC中点E,连接PO、OE,。
空间几何体(经典习题)
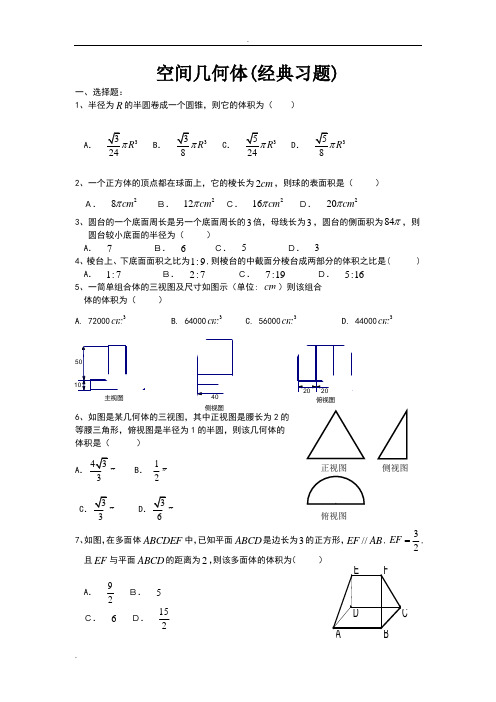
正视图 俯视图侧视图空间几何体(经典习题)一、选择题:1、半径为R 的半圆卷成一个圆锥,则它的体积为( )A .3R B .3R C .3R D .3R 2、一个正方体的顶点都在球面上,它的棱长为2cm ,则球的表面积是( ) A. 28cm π B. 212cmπC. 216cmπD. 220cm π3、圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则 圆台较小底面的半径为( )A . 7 B. 6 C. 5 D. 34、棱台上、下底面面积之比为1:9,则棱台的中截面分棱台成两部分的体积之比是( ) A . 1:7 B. 2:7 C. 7:19 D. 5:165、一简单组合体的三视图及尺寸如图示(单位: cm )则该组合 体的体积为( )A. 720003cmB. 640003cmC. 560003cmD. 440003cm62的等腰三角形,俯视图是半径为1的半圆,则该几何体的 体积是( )A. C 7、如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,//EF AB ,32EF =,且EF 与平面ABCD 的距离为2,则该多面体的体积为( )A .92B. 5 C. 6 D. 152侧视图俯视图8、一个棱锥的三视图如图,则该棱锥的体积是( ) C.4 D.89、如图是一个空间几何体的三视图,则该几何体的侧面积为( )第8题 第9题10、如图为一平面图形的直观图,则此平面图形可能是选项中的( )11、棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8 个三棱锥后,剩下的凸多面体的体积是( )A、23 B 、76 C 、45 D 、5612、在一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D 、E 、F ,且知SD :DA=SE :EB=CF :FS=2:1,若仍用这个容器盛水,则最多可盛原来水的( )A 、2923 B 、2719 C 、3130 D 、2723 13、 一空间几何体的三视图如图所示,A.2π+B. 4π+C. 23π+D. 43π+俯视图14、一个棱锥的三视图如图,则该棱锥的全面积(单位:c 2m )为( ).(A )(B )(C )(D )15、正六棱锥P-ABCDEF 中,G 为PB 的中点,则三棱锥D-GAC 与三棱锥P-GAC 体积之比为( )(A )1:1 (B) 1:2 (C) 2:1 (D) 3:216、如右图,某几何体的正视图与侧视图都是边长为1的正方形, 且体积为12。
高三高考数学复习练习82空间几何体的表面积与体积

821.一个球的表面积是16π,那么这个球的体积为( )A.163π B.323π C .16π D .24π【解析】 设球的半径为R ,因为表面积是16π,所以4πR 2=16π,解得R =2,所以体积为43πR 3=32π3. 【答案】 B2.某几何体的三视图如图所示,则其表面积为( )A .πB .2πC .3πD .4π【解析】 由三视图可知,该几何体为半径为r =1的半球体,表面积为底面圆面积加上半球面的面积,所以S =πr 2+12×4πr 2=π×12+12×4π×12=3π.故选C. 【答案】 C3.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3 D .2π【解析】 过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,故选C. 【答案】 C4.一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 2 【解析】 由空间几何体的三视图可得该空间几何体的直观图,如图所示,∴该四面体的表面积为S 表=2×12×2×1+2×34×(2)2=2+3,故选B. 【答案】 B5.(2018·太原一模)某几何体的三视图如图所示,则该几何体的表面积为( )A .6π+1B.(24+2)π4+1C.(23+2)π4+12D.(23+2)π4+1 【解析】 由几何体的三视图知,该几何体为一个组合体,其中下部是底面直径为2,高为2的圆柱,上部是底面直径为2,高为1的圆锥的四分之一,所以该几何体的表面积为4π+π+3π4+2π4+1=(23+2)π4+1,故选D. 【答案】 D6.甲几何体(上)与乙几何体(下)的组合体的三视图如图所示,甲、乙几何体的体积分别为V 1,V 2,则V 1∶V 2等于( )A .1∶4B .1∶3C .2∶3D .1∶π【解析】 由三视图知,甲几何体是半径为1的球,乙几何体是底面半径为2,高为3的圆锥,所以球的体积V 1=43π,V 2=13π×22×3=4π,所以V 1∶V 2=1∶3.故选B. 【答案】 B7.(2017·全国Ⅲ卷)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB.3π4C.π2D.π4【解析】 设圆柱的底面半径为r ,球的半径为R ,且R =1,由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形.∴r = 12-⎝⎛⎭⎫122=32.∴圆柱的体积为V =πr 2h =34π×1=3π4. 故选B.【答案】 B8.(2017·襄阳调研)如图是一个空间几何体的三视图,则该几何体的表面积为________.【解析】 由三视图可知,该几何体是一个正四棱柱挖掉一个半球所得的几何体,其中半球的底面就是正四棱柱上底面的内切圆,正四棱柱的底面边长为4,高为2,半球所在球的半径为2.所以该几何体的表面由正四棱柱的表面与半球的表面积之和减去半球的底面构成,故其表面积为(4×4×2+2×4×4)+12×(4π×22)-π×22=64+4π. 【答案】 64+4π9.(2018·乌鲁木齐二诊)已知四面体ABCD 满足AB =CD =6,AC =AD =BC =BD =2,则四面体ABCD 的外接球的表面积是________.【解析】 (图略)在四面体ABCD 中,取线段CD 的中点为E ,连接AE ,BE .∵AC =AD =BC =BD =2,∴AE ⊥CD ,BE ⊥C D.在Rt △AED 中,CD =6,∴AE =102.同理BE =102.取AB 的中点为F ,连接EF .由AE =BE ,得EF ⊥A B.在Rt △EF A 中,∵AF =12AB =62,AE =102,∴EF =1.取EF 的中点为O ,连接OA ,则OF =12.在Rt △OF A 中,OA =72.∵OA =OB =OC =OD ,∴该四面体的外接球的半径是72,∴外接球的表面积是7π. 【答案】 7π10.(2018·贵州适应性考试)已知球O 的表面积是36π,A ,B 是球面上的两点,∠AOB =60°,C 是球面上的动点,则四面体OABC 体积V 的最大值为________.【解析】 设球的半径为R ,由4πR 2=36π,得R =3.显然在四面体OABC 中,△OAB 的面积为定值,S △OAB =12×R ×32R =34R 2=934.要使三棱锥的体积最大,只需球上的点到平面OAB 的距离最大,显然,到平面OAB 距离的最大值为球的半径,所以四面体OABC 的体积的最大值V =13×934×R =934. 【答案】 93411.(2016·全国丙卷)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点.(1)证明:MN ∥平面P AB ;(2)求四面体N -BCM 的体积.【解析】 (1)证明 由已知得AM =23AD =2. 如图,取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2. 又AD ∥BC ,故TN 綊AM ,所以四边形AMNT 为平行四边形,于是MN ∥AT .因为AT ⊂平面P AB ,MN ⊄平面P AB ,所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A. 取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2= 5.由AM ∥BC 得M 到BC 的距离为5,故S △BCM =12×4×5=2 5. 所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453. 12.如图所示,在空间几何体ADE -BCF 中,四边形ABCD 是梯形,四边形CDEF 是矩形,且平面ABCD ⊥平面CDEF ,AD ⊥DC ,AB =AD =DE =2,EF =4,M 是线段AE 上的动点.(1)试确定点M 的位置,使AC ∥平面MDF ,并说明理由;(2)在(1)的条件下,平面MDF 将几何体ADE -BCF 分成两部分,求空间几何体M -DEF 与空间几何体ADM -BCF 的体积之比.【解析】(1)当M 是线段AE 的中点时,AC ∥平面MDF .理由如下:连接CE 交DF 于点N ,连接MN .因为M ,N 分别是AE ,CE 的中点,所以MN ∥AC .又因为MN ⊂平面MDF ,AC ⊄平面MDF ,所以AC ∥平面MDF .(2)将几何体ADE -BCF 补成三棱柱ADE -B ′CF ,如图所示,三棱柱ADE -B ′CF 的体积为V =S △ADE ·CD =12×2×2×4=8,则几何体ADE -BCF 的体积V ADE BCF =V ADE B ′CF -V F BB ′C=8-13×⎝⎛⎭⎫12×2×2×2=203. 因为三棱锥M -DEF 的体积V M DEF =13×⎝⎛⎭⎫12×2×4×1=43, 所以V ADM BCF =203-43=163, 所以两几何体的体积之比为43∶163=1∶4.。
高一数学空间几何体试题答案及解析

高一数学空间几何体试题答案及解析1.如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF平面EFDC.(Ⅰ)当,是否在折叠后的AD上存在一点,且,使得CP∥平面ABEF?若存在,求出的值;若不存在,说明理由;(Ⅱ)设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值.【答案】(1)存在点,;(2)当时,三棱锥的最大值.【解析】(1)与立体几何有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用空间中点、线、面的位置关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;四是利用线面平行的定义,一般用反证法;(3)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(4)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.试题解析:解:(Ⅰ)假设存在使得满足条件CP∥平面ABEF在平面内过点作交于,在平面内作直线交于点,连结 3分∵∴ 4分∵5分又∴平面∥平面 6分又∵∴,故点就是所求的点 7分又∵∴ 8分(Ⅱ)因为平面ABEF平面EFDC,平面ABEF平面EFDC=EF,又AF EF,所以AF⊥平面EFDC 10分由已知BE=x,所以AF=x(),则FD=8x.∴ 12分故当且仅当,即=4时,等号成立所以,当=4时,有最大值,最大值为 14分解法二:故所以,当=4时,有最大值,最大值为 14分【考点】(1)探究性问题;(2)求体积的最大值.2.下图中的几何体是由哪个平面图形旋转得到的()【答案】A【解析】几何体的上半部分是一个圆锥,下半部分是一个圆台,故选A【考点】简单旋转体的概念3.一个正方体的顶点都在球面上,它的棱长为,则球的表面积是()A.B.C.D.【答案】B【解析】因为一个正方体的棱长为为2,则该正方体的对角线长为.又因为该正方体的顶点都在球面上,所以球的直径就是正方体的对角线,即球的半径.又因为球的表面积.故选B.【考点】1.球的内接正方体.2.球的表面积公式.3.长方体的对称性.4.若圆锥的表面积,侧面展开图的圆心角为,则该圆锥的体积为______.【答案】【解析】设该圆锥的底面圆的半径为,母线长为,因为侧面展开图的圆心角为,所以,因为圆锥的表面积,所以,所以该圆锥的体积为【考点】本小题主要考查圆锥的侧面积和表面积的关系以及圆锥的体积计算.点评:解决本题的关键是正确运用圆锥中相应的计算公式、圆锥的侧面展开图的关系等求出,进而求出圆锥的高,然后利用圆锥的体积公式计算体积.5.某高速公路收费站入口处的安全标识墩如图1所示。
高考数学.空间几何体,点线面位置关系
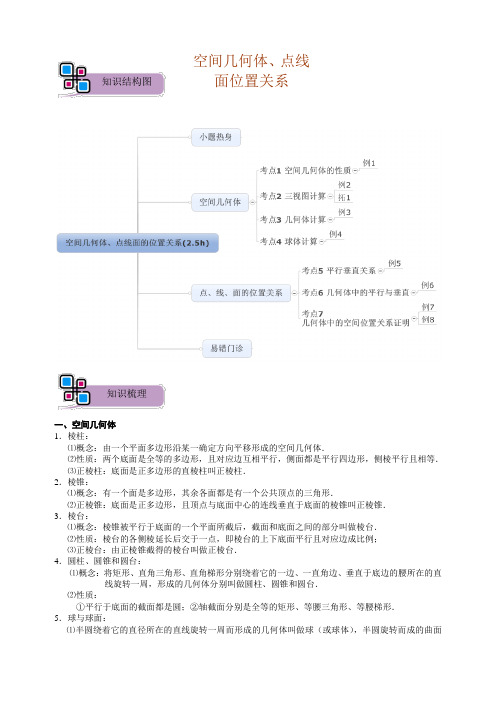
一、空间几何体 1.棱柱:⑴概念:由一个平面多边形沿某一确定方向平移形成的空间几何体.⑵性质:两个底面是全等的多边形,且对应边互相平行,侧面都是平行四边形,侧棱平行且相等. ⑶正棱柱:底面是正多边形的直棱柱叫正棱柱. 2.棱锥:⑴概念:有一个面是多边形,其余各面都是有一个公共顶点的三角形.⑵正棱锥:底面是正多边形,且顶点与底面中心的连线垂直于底面的棱锥叫正棱锥. 3.棱台:⑴概念:棱锥被平行于底面的一个平面所截后,截面和底面之间的部分叫做棱台. ⑵性质:棱台的各侧棱延长后交于一点,即棱台的上下底面平行且对应边成比例; ⑶正棱台:由正棱锥截得的棱台叫做正棱台. 4.圆柱、圆锥和圆台:⑴概念:将矩形、直角三角形、直角梯形分别绕着它的一边、一直角边、垂直于底边的腰所在的直线旋转一周,形成的几何体分别叫做圆柱、圆锥和圆台.⑵性质:①平行于底面的截面都是圆;②轴截面分别是全等的矩形、等腰三角形、等腰梯形. 5.球与球面:⑴半圆绕着它的直径所在的直线旋转一周而形成的几何体叫做球(或球体),半圆旋转而成的曲面知识梳理知识结构图空间几何体、点线面位置关系叫做球面.⑵球面被经过球心的平面截得的圆叫球的大圆,被不经过球心的平面截得的圆叫球的小圆;在球面上,两点之间的最短距离,就是经过两点的大圆在这两点间的劣弧的长度,这个弧长叫做两点间的球面距离.6.三视图:俯视图、主视图、左视图.三视图的位置关系为:俯视图在主视图下方,左视图在主视图右方. 投影规律为:主俯一样长(长对正),主左一样高(高平齐),俯左一样宽(宽相等). 7二、直线与平面的位置关系 1.平面的基本性质及推论:公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内; 公理2:经过不在同一直线上的三点,有且只有一个平面;公理3:如果不重合的两个平面有一个公共点,那么它们有且只有一条经过这个点的公共直线. 推论1:经过一条直线和直线外的一点,有且只有一个平面. 推论2:经过两条相交直线,有且只有一个平面. 推论3:经过两条平行直线,有且只有一个平面. 2.平行公理与等角定理公理4(空间平行线的传递性):平行于同一条直线的两条直线互相平行;等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. 3.空间两条直线的位置关系有:相交、平行、异面;空间直线l 与平面α的位置关系有:l α⊂、l A α=、l α∥; 空间平面α与平面β的位置关系有:αβ∥、l αβ=.4.线面平行的概念:如果直线与平面没有公共点,那么我们称这条直线与这个平面平行. 线面平行判定定理:m α⊄,m l ∥,l α⊂m α⇒∥, 线面平行性质定理:l α∥,l β⊂,m αβ=l m ⇒∥;5.面面平行的概念:如果两个平面没有公共点,我们称这两个平面平行.面面平行判定定理:a α⊂,b α⊂,a b A =,a β∥,b β∥αβ⇒∥, 面面平行性质定理:αβ∥,m αγ=,n βγ=m n ⇒∥.6.线线垂直的概念:如果两条直线相交或平移后相交于一点,且交角为直角,称两直线互相垂直. 线面垂直的概念:如果一条直线和平面内任意直线都垂直,则称这条直线与这个平面垂直. 线面垂直判定定理:a b ⊥,a c ⊥,b α⊂,c α⊂,b c A =a α⇒⊥, 线面垂直性质定理:m α⊥,n α⊥m n ⇒∥.7.面面垂直的概念:如果两个相交平面的交线与第三个平面垂直,又这两个平面与第三个平面相交所得的两条交线互相垂直,就称这两个平面互相垂直.面面垂直判定定理:l α⊂,l β⊥αβ⇒⊥.面面垂直性质定理:αβ⊥,m αβ=,n α⊂,n m ⊥n β⇒⊥.(2012北京理7)某三棱锥的三视图如图所示,该三棱锥的表面积是( )4234正(主)视图侧(左)视图俯视图A .2865+B .3065+C .56125+D .60125+【解析】 B ;(2010北京理8)如图,正方体1111ABCD A B C D -的棱长为2,动点E ,F 在棱11A B 上,动点P ,Q 分别在棱AD ,CD 上,若1EF =,1A E x =,DQ y =,DP z =(x y z ,,大于零),则四面体PEFQ 的体积( ) A .与x y z ,,都有关 B .与x 有关,与y z ,无关C .与y 有关,与x z ,无关D .与z 有关,与x y ,无关【解析】 D1、一个棱柱是正四棱柱的条件是( ) A .底面是正方形,有两个侧面是矩形 B .底面是正方形,有两个侧面垂直于底面 C .每个侧面都是全等矩形的四棱柱D .底面是菱形,且有一个顶点处的三条棱两两垂直【解析】 D ;2、 半径为R 的球内接一个正方体,则该正方体的体积是( )A . 322RB .343R C .383R D .33R小题热身真题再现QP FEB 1C 11A 1D B【解析】 C ;3、 已知球的表面积为20π,球面上有A 、B 、C 三点.如果2AB AC ==,23BC =,则球心到平面ABC 的距离为( )A .1B .2C .3D .2【解析】 A ;4、 如图,正三棱柱111ABC A B C -中,E 是BC 中点,则下列叙述正确的是( )A .1CC 与1B E 是异面直线 B .AC ⊥平面11ABB AC .AE ,11B C 为异面直线,且11AE B C ⊥D .11AC ∥平面1ABE 【解析】 C .5、 一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是( )A .3B .52C .2D .32【解析】 D6、 若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为60︒的菱形,则该棱柱的体积等于( )A .2B .22C .32D .42【解析】 B7、 正四面体ABCD 的棱长为1,E 是ABC △内一点,点E 到边AB BC CA ,,的距离之和为x ,点E 到平面DAB ,DBC ,DCA 的距离之和为y ,则22x y +=( )EDCBAA .1B 6C .53D .1712 【解析】 D ;A 1B 1C 1ABEC俯视图侧视图正视图1338、(2007湖南文6)如图,在正四棱柱 1111ABCD A B C D -中,E 、F 分别是1AB 、1BC 的中点,则以下结论中不成立的是( )A .EF 与1BB 垂直 B .EF 与BD 垂直C .EF 与CD 异面 D .EF 与11A C 异面AB CDE F A 1B 1C 1D 1【解析】 D9、 (2008辽宁卷11)在正方体1111ABCD A B C D -中,E F ,分别为棱1AA ,1CC 的中点,则在空间中与三条直线11A D ,EF ,CD 都相交的直线( )A .不存在B .有且只有两条C .有且只有三条D .有无数条【解析】 D ; 10、(2005湖北,理10)如图,在三棱柱ABC A B C '''-中,点E 、F 、H 、K 分别为AC '、CB '、A B '、B C ''的中点,G 为ABC ∆的重心.从K 、H 、G 、B '中取一点作为P ,使得该棱柱恰有2条棱与平面PEF 平行,则P 为( ) A .K B .H C .G D .B 'GK EB'A'H F ABC【解析】 C ;<教师备案>复习空间几何体的性质时应注意,有些几何体名称不同但对象相同(例如三棱锥和四面体),有些几何体看上去相同实质不同(例如四面体和空间四边形及其对角线),有些几何体名称相近关系密切却有细微的差异(例如四棱柱家族),务必将名称与几何体严格对应并熟悉相应性质.下图为四棱柱家族的详细关系图:复习空间位置关系的判定应注意解题思路的梳理和过程书写的规范,每个步骤都应有明确的定义或定理作为基础,切忌“想当然”.考点1:空间几何体的性质【例1】 ⑴四棱锥成为正棱锥的一个充分但不必要条件是( )A .各侧面是正三角形B .底面是正方形C .各侧面三角形的顶角为45度D .顶点在底面的射影是底面对角线的交点 ⑵下面关于四棱柱的四个命题:①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱; ③若四个侧面两两全等,则该四棱柱为直四棱柱;④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱. 其中,真命题的序号是______.⑶在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点, 这些几何形体可以是_________(写出所有正确结论的编号). ①不是正方形的矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;经典精讲7.1空间几何体平行六面体 四棱柱 底面是平行四边形侧棱与 底面垂直 正四棱柱 底面是平行四边形直平行六面体底面为 正方形 直四棱柱 侧棱与 底面垂直 底面为 长方形 长方体 底面是正方形 侧面也为正方形 正方体棱长都相等的长方体④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.【解析】 ⑴A ;⑵ ②④; ⑶①③④⑤;考点2:三视图计算 【例2】 ⑴(2010北京东城一模)下图是一个几何体的三视图,则该几何体的体积为_________.俯视图侧(左)视图正(主)视图222211⑵(2011北京二中高三月考5)下图为一个几何体的三视图,尺寸如图所示,则该几何体的表面积为( )(不考虑接触点) A .63π++ B .1834π++ C .1823π++ D .32π+ ⑶(2009辽宁15)设某几何体的三视图如图(长度单位m ),则该几何体的体积为_____3m . ⑷(2012海淀二模理7)某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )A .203B .43C .6D .43322221133222左视俯视图主视图第⑵题 第⑶题 第⑷题【解析】 ⑴43; ⑵C ; ⑶ 4; ⑷A ;<教师备案>根据三视图进行体积计算时,首先确定几何体的形状(棱柱或棱锥等),然后获得所需的数据,最后根据公式计算即可.由于计算底面积所需数据和几何体的高均可从三视图中直接获得,因此以三视图为基础的几何体体积计算是比较容易的.<教师备案>相对于体积计算,根据三视图进行表面积计算是比较困难的,因为相关数据很难从三视图中直接获得,需要先将三视图还原为直观图,再将直观图分解为展开图,依次计算各个表面的面积,最后求和.这个过程中,三视图还原直观图是最关键的,各个表面分别计算面积是最麻烦的.【拓1】 如果一个几何体的三视图如图所示,则此几何体的表面积是( )A .()280162cm + B .296cmC .()296162cm +D .2112cm【解析】 A 考点3:几何体计算【例3】 ⑴(2009陕西10)若正方体的棱长为2,则以该正方体各个面的中心为顶点的凸多面体的体积为( )A .26B .23C .33D .23⑵在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1:3,则锥体被截面所分成的两部分的体积之比为( )A .1:3B .1:9C .1:33D .()1:331- ⑶如图,在正三棱柱111ABC A B C -中,D 为棱1AA 的中点.若截面1BC D △是面积为6的直角三角形,则此三棱柱的体积为_______.【解析】 ⑴ B ;⑵ D ;⑶83俯正视图侧视图4442俯视图44C 1B 1A 1DCBA考点4:球体计算【例4】 ⑴长方体的三个相邻面的面积分别为2,3,6,这个长方体的顶点都在同一个球面上,则这个球面的表面积为( )A .7π2 B .56π C .14π D .64π⑵(2012西城二模13)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,该几何体的体积是_____; 若该几何体的所有顶点在同一球面上,则球的表面积是_____.⑶(2010课标全国10)设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面积为( )A .2πaB .27π3aC .211π3a D .25πa【解析】 ⑴C ;⑵13π3,; ⑶ B考点5:平行垂直关系【例5】 ⑴ 已知m 、n 、l 为直线,α、β、γ为平面,有下列四个命题:①若m α∥,m β∥,则αβ∥;②l n ⊥,l m ⊥,n α⊂,m α⊂,则l α⊥; ③αβ⊥,αγ∥,则βγ⊥;④m α⊂,n β⊂,αβ⊥,则m n ⊥.其中正确命题的个数是( ) A .0 B . 1 C .2 D .3 ⑵设l 、m 、n 表示三条直线,α、β、γ表示三个平面,给出下列四个命题:①若l α⊥,m α⊥,则l m ∥;②若m β⊂,n 是l 在β内的射影,m l ⊥,则m n ⊥;③若m α⊂,m n ∥,则n α∥;④若αγ⊥,βγ⊥,则αβ∥. 其中真命题为( )A .①②B .①②③C .①②③④D .③④【解析】 ⑴ B ;⑵ A ;7.2点、线、面的位置关系俯视图侧视图正视图考点6:几何体中的平行与垂直【例6】 ⑴下列四个正方体图形中,A B ,为正方体的两个顶点,M 、N 、P 分别为其所在棱的中点,能得出AB ∥平面MNP 的图形有__________.ABPNMAB PNMA BPNMBAMNP① ② ③ ④ ⑵ 过平行六面体1111ABCD A B C D -任意两条棱的中点作直线,其中与平面11DBB D 平行的直线共有( )A .4条B .6条C .8条D .12条 ⑶在正方体1111ABCD A B C D -中,M 是1AA 的中点,N 是线段AB上一点,若1MN MC ⊥,则( )A .12AN AB = B .14AN AB = C .13AN AB = D .34AN AB =⑷如图,PA ⊥平面ABC ,90ABC ∠=︒,则图中互相垂直的平面有( )CBAPA .2对B .3对C .4对D .5对【解析】 ⑴①④;⑵ D ⑶B ; ⑷B ;NMA B CDA 1B 1C 1D 1考点7:几何体中的空间位置关系证明【例7】 (2010丰台二模文16)如图,在四棱锥S ABCD -中,底面ABCD 是菱形,SA ABCD ⊥底面,M 为SA 的中点,N 为CD 的中点. ⑴ 证明:平面SBD ⊥平面SAC ; ⑵ 证明:直线MN SBC 平面‖.NMSDCBA【解析】 ⑴ ∵ABCD 是菱形,∴BD AC ⊥,∵SA ⊥底面ABCD ,∴BD SA ⊥,∵SA 与AC 交于A ,∴BD ⊥平面SAC ,∵BD ⊂平面SBD ,∴平面SBD ⊥平面SAC . ⑵ 取SB 中点E ,连接ME ,CE , ∵M 为SA 中点,∴ME AB ∥且12ME AB =, 又∵ABCD 是菱形,N 为CD 的中点,∴CN AB ∥且1122CN CD AB ==,∴CN EM ∥,且CN EM =, ∴四边形CNME 是平行四边形, ∴MN CE ∥,又MN ⊄平面SBC ,CE ⊂平面SBC , ∴直线MN ∥平面SBC .(也可以取AB 中点F ,通过面MNF ∥面SBC 来证MN ∥面SBC )【例8】 如图,在三棱柱111ABC A B C -中,AB BC ⊥,1BC BC ⊥,1AB BC =,E F G ,,分别为线段1111AC AC BB ,,的中点, 求证:⑴平面ABC ⊥平面1ABC ;⑵EF ∥平面11BCC B ;⑶GF ⊥平面11AB C .【解析】 ⑴ ∵BC AB ⊥,1BC BC ⊥,1AB BC B =,∴BC ⊥平面1ABC ,又BC ⊂平面ABC , ∴平面ABC ⊥平面1ABC ; ⑵∵111AE EC A F FC ==,,∴1EF AA ∥. ∵11BB AA ∥,∴1EF BB ∥.∵EF ⊄平面11BCC B ,∴EF ∥平面11BCC B ; ⑶ 连接EB (图略),则四边形EFGB 为平行四边形, ∴GF BE ∥.∵1AB BC =,1AE EC =,∴1BE AC ⊥,∴1GF AC ⊥. 又∵BC ⊥平面1ABC ,11BC B C ∥,∴11B C ⊥平面1ABC . ∵BE ⊂平面1ABC ,∴11B C BE ⊥.∴11GF B C ⊥.C 1B 1A 1GFE CB AEAB CD S MN∵1111B C AC C =,∴GF ⊥平面11AB C .<教师备案>空间距离的计算分为“直接法”、“间接法”和“向量法”:直接法需要找到垂线段的位置,对添加辅助线的技巧要求比较高,找到垂线段后利用解三角形、三角函数和勾股定理计算;间接法需要找到适当的三棱锥,通常不需要添加辅助线,但面积和体积的计算比较麻烦;向量法需要计算法向量,相应课程中会有详细的复习和练习.⑵中由于垂线段的位置比较容易确定,使用的是直接法;若求1A 到11EB D 的距离,则使用间接法比较合适.空间几何体体积的计算分为“直接法”和“间接法”:直接法使用几何体对应的公式直接计算;间接法适合规范几何体中分割出的“四面悬空”的几何体,通过整体减去不需要的部分的方法求解.⑶可以将两种方法均练习一下,用间接法需要连结DE EF ,.a b ,为两异面直线,下列结论正确的是 ( ) A .过不在a b ,上的任何一点,可作一个平面与a b ,都平行 B .过不在a b ,上的任一点,可作一直线与a b ,都相交 C .过不在a b ,上任一点,可作一直线与a b ,都平行 D .过a 可以并且只可以作一个平面与b 平行【解析】 D ;一、选择题1、 (2008山东文理6)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )2322俯视图侧(左)视图正(主)视图A .9πB .10πC .11πD .12π【解析】 D ; 课后习题2、(2006江西)如图,在四面体ABCD 中,截面AEF 经过四面体的内切球(与四个面都相切的球)球心O ,且与BC ,DC 分别截于E 、F ,如果截面将四面体分成体积相等的两部分,设四棱锥A BEFD -与三棱锥A EFC -的表面积分别是1S ,2S ,则必有( )A .12S S <B .12S S >C .12S S =D .12S S ,的大小关系不能确定【解析】 C .3、 如图,在等腰梯形ABCD 中,2260AB DC DAB ==∠=︒,,E 为AB 的中点,将ADE △ 与BEC △分别沿,ED EC 向上折起,使,A B 重合于点P ,则三棱锥P DCE -的外接球的体积为( )DECBAA B CD【解析】 C .4、 (2001年全国高考)一间民房的屋顶有如下图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法屋顶面积分别为1P 、2P 、3P .若屋顶斜面与水平面所成的角都是a ,则( )A .321P P P =>B .321P P P >=C .321P P P >>D .321P P P ==【解析】 D二、填空题5、 (2008全国II 理16)平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:充要条件①; 充要条件② .(写出你认为正确的两个充要条件)【解析】 两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.6、 (2010湖北13)圆柱形容器内部盛有高度为8cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是______cm .【解析】 47、 (2008福建15) 3是 .ABCD【解析】 9π;8、 设α、β、γ是三个不重合的平面,l 是直线,给出下列四个命题:①若αβ⊥,l β⊥,则l α∥;②若l α⊥,l β∥,则αβ⊥;③若l 上有三点到α的距离相等,且l α⊄,则l α∥;④若αβ⊥,αγ∥,则γβ⊥. 其中正确命题的序号是______________.【解析】 ②③④;三、解答题9、 如图,正方形O A B C ''''的边长为1,它是水平放置的一个平面图形的直观图.请画出原来的平面几何图形的形状,并求原图形的周长与面积.x 'y 'A 'B 'C 'O '【解析】 周长为8,面积为2210、 把四个半径都是1的球中的三个放在桌面上,使它两两外切,然后在它们上面放上第四个球,使它与前三个都相切,求第四个球的最高点与桌面的距离. 【解析】 第四个球的最高点与桌面的距离为2.11、 如图,在底面是平行四边形的四棱锥P ABCD -中,点E 在PD 上,且:2:1PE ED =,F 为棱PC 的中点.求证:BF ∥平面AECE PDABCF【解析】 (法一)取PE 的中点M ,连结FM ,则FM ∥CE ①由12EM PE ED ==,知E 是MD 的中点.连结,BM BD ,设BD AC O =,则O 为BD 的中点. ∴BM ∥OE ②由①,②知,平面BFM ∥平面AEC∵BF ⊂平面BFM ,∴BF ∥平面AEC .(法二)∵11()22BF BC CP AD CD DP =+=++1322AD CD DE =++13()()22AD AD AC AE AD =+-+-31.22AE AC =- ∴BF 、AE 、AC 共面.又BF ⊄平面AEC ,从而BF ∥平面AEC12、 如图,在五面体ABCDEF 中,点O 是矩形ABCD 的对角线的交点,平面CDE 是等边三角形,棱12EF BC ∥.⑴ 证明:FO ∥平面CDE ; ⑵设BC =,证明:EO ⊥平面CDF .【解析】 ⑴ 取CD 的中点M .连结OM .在矩形ABCD 中,12OM BC ∥,又12EF BC ∥,则EF OM ∥.连结EM ,于是四边形EFOM 为平行四边形, ∴FO EM ∥.又∵FO ⊄平面CDE ,且EM ⊂平面CDE ,MOABCDEFFEDCBAOOFM CBADPE∴FO∥平面CDE.⑵连结FM,CF,在等边CDE△中,CM DM=,∴EM CD⊥且12EM BC EF===.因此平行四边形EFOM为菱形,从而EO FM⊥.∵CD OM⊥,CD EM⊥,∴CD⊥平面EOM,又∵EO⊂平面EOM,∴CD EO⊥.而FM CD M=,所以EO⊥平面CDF.13、已知三棱锥P ABC-中,PC⊥底面ABC,AB BC=,D F,分别为AC PC,的中点,DE AP⊥于E.⑴求证:AP⊥平面BDE;⑵求证:平面BDE⊥平面BDF;⑶若:1:2AE EP=,求截面BEF分三棱锥P ABC-所成两部分的体积比.FEB DCAP【解析】⑴∵AB BC=,D为AC中点,∴BD AC⊥又PC⊥底面ABC,∴PC BD⊥∵PC AC C=,∴BD⊥平面PAC,∴BD AP⊥.又DE AP⊥,∴AP⊥平面BDE.⑵∵D F,为AC PC,的中点,∴DF AP∥.结合⑴可知DF⊥平面BDE.又DF⊂面BDF,∴平面BDE⊥平面BDF.⑶1:2.。
高考真题(立体几何中空间角问题[题目])
![高考真题(立体几何中空间角问题[题目])](https://img.taocdn.com/s3/m/9d2b391cdaef5ef7bb0d3c62.png)
解答题1. 如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是菱形,2,60AB BAD =∠=o .(Ⅰ)求证:BD ⊥平面;PAC(Ⅱ)若,PA AB =求PB 与AC 所成角的余弦值;(Ⅲ)当平面PBC 与平面PDC 垂直时,求PA 的长.2. 如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,四边形ABCD 中,AB ⊥AD ,AB +AD =4,CD =2,︒=∠45CDA .(I )求证:平面P AB ⊥平面P AD ;(II )设AB =AP .(i )若直线PB 与平面PCD 所成的角为︒30,求线段AB 的长;(ii )在线段AD 上是否存在一个点G ,使得点G 到点P ,B ,C ,D 的距离都相等?说明理由。
3. 如图5.在椎体P -ABCD 中,ABCD 是边长为1的棱形,且∠DAB =60︒,2PA PD ==,PB =2, E ,F 分别是BC ,PC 的中点.(1) 证明:AD ⊥平面DEF ;(2) 求二面角P -AD -B 的余弦值.4. 如图,已知正三棱柱111ABC A B C -的各棱长都是4,E 是BC 的中点,动点F 在侧棱1CC 上,且不与点C 重合.(Ⅰ)当CF =1时,求证:EF ⊥1A C ;(Ⅱ)设二面角C AF E --的大小为θ,求tan θ的最小值.A B DC FPE5. 如图,在圆锥PO中,已知PO=2,⊙O的直径2AB=,C是»AB的中点,D为AC 的中点.(Ⅰ)证明:平面POD⊥平面PAC;(Ⅱ)求二面角B PA C--的余弦值。
6. 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=12 PD.(I)证明:平面PQC⊥平面DCQ;(II)求二面角Q—BP—C的余弦值.8. 如图,四棱锥P ABCD -中,底面ABCD 为平行四边形,60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD .(I )证明:PA BD ⊥;(II )若PD =AD ,求二面角A -PB -C 的余弦值.9. 在如图所示的几何体中,四边形ABCD 为平行四边形,∠ ACB =90︒,EA⊥平面ABCD,EF ∥AB,FG∥BC,EG∥AC.AB=2EF.(Ⅰ)若M是线段AD的中点,求证:GM∥平面ABFE;(Ⅱ)若AC=BC=2AE,求二面角A-BF-C的大小.10. 如图,在ABC ∆中,60,90,ABC BAC AD ∠=∠=o o 是BC 上的高,沿AD 把ABC ∆折起,使90BCD ∠=o 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间几何体和三视图、表面积及体积1棱柱的体积公式:V=Sh,其中S是棱柱的底面积,h为2棱锥的体积公式:V= 13Sh,其中S是棱锥的底面积,h为高.1.(2016全国一卷(7))如图,学.科网某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3,则它的表面积是(A)17π (B)18π (C)20π (D)28π2.(2016全国三卷10)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为(A)18+(B)54+(C)90 (D)813.(2016全国二卷(7))如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A)20π(B)24π(C)28π(D)32π4.(2016浙江9).某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm2,体积是______cm3.5.(2016天津(3))将一个长方形沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为6.(2016四川)已知某三菱锥的三视图如图所示,则该三菱锥的体积是。
侧视图俯视图7.(2016山东5)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为(A)12+π33(B)1+π33(C)1+π36(D)1+π68.(2016北京11)某四棱柱的三视图如图所示,则该四棱柱的体积为___________.1.[2015·全国卷Ⅰ改编] 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图10-1所示.若该几何体的表面积为16+20π,则r=________.图10-12.[2015·安徽卷改编] 一个四面体的三视图如图10-2所示,则该四面体的表面积是________.图10-23.[2014·浙江卷改编] 某几何体的三视图(单位:cm)如图10-3所示,则此几何体的表面积是________.图10-34.[2015·浙江卷改编] 某几何体的三视图如图10-4所示(单位:cm),则该几何体的体积是________.图10-45.[2015·重庆卷改编] 某几何体的三视图如图10-5所示,则该几何体的体积为________.图10-56.[2015·天津卷] 一个几何体的三视图如图10-6所示(单位:m),则该几何体的体积为________m3.图10-67.[2015·山东卷改编] 在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2,将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为________.8.[2015·江苏卷] 现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为________.9.[2015·上海卷] 若圆锥的侧面积与过轴的截面面积之比为2π,则其母线与轴的夹角的大小为________.10.[2015·全国卷Ⅱ改编] 已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点.若三棱锥O -ABC体积的最大值为36,则球O的表面积为________.考点一三视图与直观图图10-7在如图10-7所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①②③④的四个图,则该四面体的正视图和俯视图分别为()图10-8A.①和②B.③和①C.③和④D.④和②[小结] 找空间几何体的三视图,关键要抓住空间几何体的顶点在投影面上的正投影,再看各棱在投影面上的正投影;根据三视图判断空间几何体的形状,基本方法是根据三视图的画法进行逆向思维,借助已知的空间几何体的结构特点、结合题目要求进行肯定或者否定.要特别注意三视图中“眼见为实、不见为虚”的画法规则.若某几何体的三视图如图10-9所示,则此几何体的直观图是()图10-9图10-10考点二几何体的表面积与体积图10-11一个简单几何体的三视图如图10-11所示,其中正视图是一个正三角形,俯视图是等腰直角三角形,则该几何体的体积为________,表面积为________.[小结] 高考试题中求体积和表面积的试题往往与空间几何体的三视图结合,此时要根据空间几何体的三视图还原空间几何体,弄清楚空间几何体的结构再进行计算.体积的计算需要空间几何体的底面积和高,表面积的计算需要把各个面的结构弄清楚,分别计算各个面的面积,再求和.已知某几何体的三视图如图10-12所示,则该几何体的体积是__________,表面积是________.图10-12高考易失分题11 三视图、直观图、体积问题的综合范例某篮球架的底座的三视图如图10-13所示,则其体积为()图10-13A.470+10 303B.175C.180 D.295+10 2失分分析该类试题容易把空间几何体的结构弄错,求体积时不能准确割补、求表面积时出现遗漏或重复等错误.高考预测某几何体的三视图如图10-14所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积是()图10-14A.2 B. 3 C.3 3 D.3考点三多面体与球图10-15如图10-15所示,在等腰梯形ABCD中,AB=2CD=2,∠DAB=60°,E为AB的中点.将△ADE与△BEC分别沿ED,EC向上折起,使A,B重合于点P,则三棱锥P-DCE的外接球的体积为()A.6π8 B.6π6 C.6π4 D.6π2[小结] 球中内接一个多面体是高考的一个重要命题点.如果一个多面体内接于一个球,那么它的各个多边形都是圆的内接多边形,球心到各个顶点的距离都等于球的半径.已知球的直径SC=4,A,B是该球球面上的两点,且AB=3,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为()A.3 3 B.2 3C. 3 D.1参考答案■ 核心知识聚焦1.2 [解析] 由三视图可知,此组合体的前半部分是一个底面半径为r ,高为2r 的半圆柱(水平放置),后半部分是一个半径为r 的半球,其中半圆柱的一个底面与半球的半个圆面重合,所以此几何体的表面积为2r ·2r +12πr 2+12πr 2+πr ·2r +2πr 2=4r 2+5πr 2=16+20π,解得r=2.2.2+3 [解析] 四面体的直观图如图所示,设O 是AC 的中点,则OP =OB =1,因此PB =2,于是S △PAB =S △PBC =34×(2)2=32,S △PAC =S △ABC =12×2×1=1,故四面体的表面积S =2×1+2×32=2+ 3.3.138 cm 2 [解析] 此几何体是由长方体与三棱柱组合而成的,其直观图如图,所以该几何体的表面积为2×(4×3+6×3+6×4)+2×12×3×4+4×3+3×5-3×3=138(cm 2).4.323cm 3 [解析] 该几何体为一个正方体和一个正四棱锥的组合体,故该几何体的体积V =23+13×2×2×2=323(cm 3).5.13+π [解析] 由三视图知,该几何体为一个半圆柱与一个三棱锥的组合体,其中半圆柱的底面圆的半径为1、高为2,三棱锥的底面为一个等腰直角三角形,斜边上的高为1,所以该几何体的体积V =13×12×2×1×1+12π×12×2=13+π.6.83π [解析] 根据三视图可知几何体是圆柱与两个圆锥的组合体,其体积V =π×12×2+2×13×π×12×1=83π(m 3).7.5π3[解析] 旋转后的几何体为一个底面半径为1,高为2的圆柱挖去一个底面半径为1,高为1的圆锥,所求几何体的体积为π×12×2-13π×12×1=53π.8.7 [解析] 设新的底面半径为r ,则13π×52×4+π×22×8=13πr 2×4+πr 2×8 ,即283πr 2=1003π+32π,解得r =7. 9.60° [解析] 设圆锥的底面半径为r ,高为h ,母线为l ,则其侧面积为πrl ,过轴的截面面积为rh .由题意可知,πrl rh =2π,得h l =12,故圆锥的母线与轴的夹角为60°. 10.144π [解析] 如图所示,当OC ⊥平面AOB 时,三棱锥O ABC 的体积最大,此时V三棱锥O -ABC=V 三棱锥C -AOB =13S △AOB ·R =16R 3=36,所以R =6,所以S 球=4πR 2=144π.■ 考点考向探究例1 D [解析] 由题意,在正方体中还原四面体的直观图如图所示.故选D.变式题 A [解析] 该几何体是正方体的一部分,易知选项A 正确. 例2333+7+1 [解析] 易知,该几何体是一个三棱锥,且该三棱锥的高为3,底面为底边边长为2,高为1的等腰直角三角形,故易求得该几何体的体积和表面积分别为33和3+7+1. 变式题 84219+3 412[解析] 原几何体为一个长、宽、高分别为6,3,5的长方体砍去一个高为3,底面为直角边分别为3,4的直角三角形的三棱锥,因此该几何体的体积为3×6×5-13×12×3×4×3=90-6=84,表面积为2×(6×3+5×3+5×6)-12×3×4×2-12×3×3+12×3 2×32+42-⎝⎛⎭⎫3 222=219+3 412.高考易失分题11范例 B [解析] 其直观图如图所示,故所求体积为10×⎝⎛⎭⎫12×1+6+52×1=352×10=175. 高考预测 B [解析] 该几何体的直观图如图所示,其体积为13×12×(1+2)×2×3= 3.例3 A [解析] 折起后的图形是棱长为1的正四面体,将其放在正方体中,其直观图如图所示.它可以看作是一个棱长为22的正方体被截去四个角后得到的几何体,可求得该几何体的外接球的半径为12×12+12+12=64,故所求球的体积为4π3×⎝⎛⎭⎫643=6π8.变式题 C [解析] 如图,设球心为O ,△ABC 的外心为O ′.根据球的性质可知,OO ′⊥平面ABC ,且∠SBC =∠SAC =90°,所以BC =AC =2.在△ABC 中,根据余弦定理得cos ∠ACB =4+4-32×2×2=58,所以sin ∠ACB =398.根据正弦定理得3398=2r (r 为△ABC 外接圆半径),所以r =413,所以OO ′=4-1613=3613=613.所以棱锥S -ABC 的体积为13×12×2×2×398×1213=3.■ 教师备用例题例1(配例1使用)[2015·全国卷Ⅱ] 一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.15[解析] D几何体的直观图为正方体ABCD-A1B1C1D1截去了一个三棱锥A-A1B1D1,如图所示.易知V三棱锥A-A1B1D1=16V正方体,所以V三棱锥A-A1B1D1VB1D1C1ABCD=15,故选D.例2(配例2使用)[2015·陕西卷] 一个几何体的三视图如图所示,则该几何体的表面积为()A.3πB.4πC.2π+4 D.3π+4[解析] D该几何体是底面半径为1、母线长为2的圆柱被其轴截面截开的半个圆柱,其表面积为12×2π×1×2+2×12×π×12+2×2=3π+4.例3(配例2使用)[2015·全国卷Ⅰ] 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图所示,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()A.14斛B.22斛C.36斛D.66斛[解析] B由题意,题中图形为四分之一圆锥,设圆锥的底面半径为R,则由πR2=8得R=16π,所以V米=14V圆锥=14×13×π×⎝⎛⎭⎫16π2×5=3203π≈3209(立方尺),所以3209÷1.62≈21.95≈22(斛).。
