系统动刚度的概念
机械系统的静态与动态刚度分析

机械系统的静态与动态刚度分析在机械设计领域中,静态与动态刚度分析是非常重要的工作,它可以帮助工程师评估机械系统在不同工况下的刚度表现并进行优化。
本文将简要介绍机械系统的静态与动态刚度分析的概念、方法和应用。
1. 静态刚度分析静态刚度分析是指机械系统在静止工况下,受到外力作用时的刚度表现。
在进行静态刚度分析时,需要考虑系统的刚性、弹性和弯曲等因素。
一般情况下,静态刚度可以通过计算机辅助设计(CAD)软件进行仿真,或者通过实验测试得到。
静态刚度分析有助于工程师进行结构优化。
通过分析机械系统的刚度,可以确定系统的强度和刚性是否满足设计要求,以及是否存在应力过大或变形过大的问题。
如果系统刚度不足,可能会导致机械设备在工作过程中出现振动、共振或破坏等问题,从而影响系统的性能和寿命。
2. 动态刚度分析动态刚度分析是指机械系统在运动工况下,受到外力作用时的刚度表现。
与静态刚度分析相比,动态刚度分析需要考虑机械系统的惯量、阻尼以及自振频率等因素。
动态刚度分析可以帮助工程师评估机械系统的振动特性。
通过分析系统的自振频率和振动模态,可以确定可能出现的共振现象,并采取相应的措施进行避免或抑制。
此外,动态刚度分析还可以用于预测机械系统在工作过程中的振动幅值和共振频率,从而提前评估并解决振动相关的问题。
3. 刚度优化在机械系统设计中,静态与动态刚度分析可用于刚度优化。
刚度优化旨在提高机械系统的刚度,以满足设计要求并改善系统的性能。
优化方法一般包括结构改造、材料选择和加工工艺优化等。
在进行刚度优化时,需要权衡刚性和重量之间的关系。
增加结构刚度通常需要增加材料的厚度、强度或数量,从而增加系统的重量。
因此,刚度优化需要综合考虑机械系统的性能要求和重量限制,并进行合理的权衡。
4. 应用实例静态与动态刚度分析在实际应用中具有广泛的应用。
例如,汽车工程师可以使用刚度分析来评估汽车底盘的刚度表现,在遇到减震问题时进行改进。
此外,航空航天工程师可以使用刚度分析来评估飞机结构在起飞、飞行和降落等工况下的刚度表现,确保飞机的结构稳定性和安全性。
什么是动刚度

什么是动刚度同理,单自由度系统的动刚度曲线也有类似性质在低频段,动刚度接近静刚度,幅值是k,表明共振频率以下的频率段主要用占主导地位的刚度项来描述。
如果作用在系统的外力变化很慢,即外力变化的频率远小于结构的固有频率时,可以认为动刚度和静刚度基本相同。
在高频段,动刚度的幅值为ω2m,表明共振频率以上的频率段主要用占主导地位的质量项来描述,这是因为质量在高频振动中,产生很大的惯性阻力。
当外力的频率远大于结构的固有频率时,结构则不容易变形,即变形较小,此时结构的动刚度相对较大,也就是抵抗变形的能力强。
在共振频率处动刚度的幅值下降明显,其幅值为ωc,表明在共振频率处主要受阻尼控制。
而在共振频率处,我们知道,结构很容易被外界激励起来,结构的变形最大,因而结构抵抗变形的能力最小,也就是动刚度最小。
3. 多自由度动刚度单自由度系统是基础,但现实世界中的系统大多数都是多自由度系统,因此,我们测量出来的动刚度也是多自由度的动刚度。
下图为多自由度系统的同一位置的加速度频响函数(加速度导纳)和该点的动刚度曲线。
多自由度系统的驱动点FRF存在多个共振峰和反共振峰,在共振峰处,对结构施加很小的激励能量,结构就会产生非常大的振动(变形),因而在共振峰处,结构很容易被激励起来,结构的变形大,抵抗变形的能力弱,也就是动刚度小。
在反共振峰所对应的频率处进行激励,即使激励能量再大,结构也没有响应或者响应很微弱,也就是说在反共振峰所对应的频率处,结构很难被激励起来,结构的变形小,抵抗变形的能力强,因此,动刚度大。
从上图可以看出,频响函数共振峰对应的是动刚度曲线的极小值,也就是说频响函数幅值大的频率处,动刚度小。
在反共振峰处,动刚度大,二者刚好相反。
4. 原点动刚度原点动刚度IPI(Input Point Inertance,IPI):概念上类似原点(或称作驱动点)频响函数,指的是同一位置、同一方向上的激励力与位移之比,主要测量与车身接附点处的原点动刚度,比如车身与发动机悬置、副车架、悬架连接处、排气挂钩处等位置的局部动刚度,考虑的是在所关注的频率范围内该接附点局部区域的刚度水平,过低必须引起更大的噪声,因此,该性能指标对整车的NVH性能有较大的影响。
动刚度和一阶模态-概述说明以及解释

动刚度和一阶模态-概述说明以及解释1.引言1.1 概述概述:动刚度和一阶模态是结构动力学领域中常被讨论和研究的两个重要概念。
动刚度是指结构在受到外部力作用下发生变形的能力,它是结构刚度在动力学问题中的体现。
一阶模态则是指结构在自由振动时,最低频率下的振动模式。
这两个概念在结构分析、设计和优化中具有重要的作用,对于确保结构的安全性、稳定性和性能具有不可忽视的影响。
动刚度与一阶模态之间存在紧密的关系。
一方面,动刚度决定了结构的振动特性,包括固有频率、模态形态和振动幅值等。
结构的刚度越大,其固有频率越高,振动幅值越小。
另一方面,一阶模态反过来也影响了结构的动刚度。
一阶模态所对应的固有频率是结构自由振动的最低频率,而自由振动对应的形变和变形会影响结构的刚度分布,进而影响整个结构的动刚度。
动刚度和一阶模态在工程实践中具有广泛的应用。
动刚度分析可以帮助工程师评估结构在外部载荷下的响应和变形情况,为结构设计和优化提供依据。
一阶模态分析则可以用于确定结构的固有频率,为结构抗震设计和振动控制提供参考。
例如,在桥梁设计中,动刚度分析可以帮助确定桥梁的刚度需求,从而满足桥梁在运行过程中的荷载要求;而一阶模态分析可以帮助设计人员理解桥梁的振动特性,并采取相应的措施来避免共振现象的发生。
本文将重点探讨动刚度与一阶模态的关系,分析它们在结构动力学中的相互影响关系,并结合实际案例进行分析。
同时,本文还将对动刚度和一阶模态的重要性进行总结,并强调它们之间关系的研究意义。
最后,本文将提出未来研究的方向,以期为相关领域的研究者提供参考和启示。
文章结构部分的内容可以如下所示:1.2 文章结构本文主要分为三个部分:引言、正文和结论。
引言部分将首先对本文的主题进行概述,介绍动刚度和一阶模态的基本概念和定义。
接着,文章将介绍本文的结构和各个章节的内容安排,使读者能够更好地了解整篇文章的逻辑结构。
正文部分分为三个小节。
首先,将详细阐述动刚度的定义和概念,探讨其在工程和物理学中的重要性。
起重机的动刚度及其测试方法

的单自由度系统 (如图 1 所示) ,其动刚度 KD 可以 表示为 :
KD = K〔(1 - λ2) + 2 ξi λ〕
(1)
式中 K ———系统的静刚度
ξ———阻尼比
ξ= C/ (2 mωn) C ———阻尼系数
m ———系统质量 ωn ———系统固有频率 ωn = K/ m = 2πf n
f n ———结构的自振频率 λ———频率比
实测时 ,为了快速 、准确地得到起重机动刚度 , 主要采用以下两种方法 :
起重机在起吊 、卸载以及突然起制动过程中 ,均 会引起冲击动载 ,使其产生一定振幅和一定时间的 衰减振动 。起重机对动刚度的要求主要是为了控制
由于冲击动载所引起的振幅和振动的衰减时间 。由
于起重机结构 、材质等因素的不同 ,阻尼比在一个较 大范围内进行变化 ,而且难以进行理论估计 ,这就给 直接计算动刚度带来了困难 。
参 考 文 献 1 起重机设计手册 1 北京 :机械工业出版社 ,19801 2 张阿舟 1 振动控制工程 1 宇航出版社 ,19891 3 机械工程手册 1 北京 :机械工业出版社 ,19781 4 500t/ 300t/ 40t 双向门式起重机测试报告 1 太原重型机
械研究所 ,19891
图 1 受简谐激振力的单自由度系统 图 2 单自由度系统的动刚度曲线
4 结束语
该微机监控系统在建设部长沙机械研究院设计 的 Q TZ2800 型塔式起重机上作了现场试验 ,结果证 明该微机电控系统工作稳定 、可靠 ,抗干扰能力强 , 功能强大 ,司机可以通过液晶屏随时掌握塔式起重 机的工作参数 ,起吊重物的自动就位误差小于 10cm ,各项功能达到了设计要求 。
由于 k = mω2n ,ωn = 2πf n ,则式 (4) 可变为
位移阻抗(动刚度)等

位移阻抗,也称为动刚度,是衡量系统动态性能的重要参数。
它表示系统在受到外部激励时,抵抗位移的能力。
这个参数与系统的质量、阻尼和刚度等因素密切相关。
一个具有高位移阻抗的系统,意味着它在受到外部激励时,能够保持较小的位移响应。
这种系统通常具有较好的稳定性,能够在各种动态环境下保持其功能和性能。
而低位移阻抗的系统则更容易发生较大的位移,可能导致系统失稳或产生不希望的振动。
在工程设计中,了解系统的位移阻抗至关重要。
通过分析位移阻抗,工程师可以预测系统在不同工作条件下的动态行为,从而优化设计。
例如,如果一个机械装置的位移阻抗较低,可能需要在设计中加入额外的支撑结构或阻尼器来提高其稳定性。
此外,在控制系统设计中,位移阻抗也是重要的考虑因素。
在主动控制技术中,了解位移阻抗有助于选择合适的控制策略和调整控制增益。
高位移阻抗的系统可能需要更精确的控制和调节,以实现预期的动态性能。
综上所述,位移阻抗作为描述系统动态性能的关键参数,对于工程设计和控制系统设计具有重要的指导意义。
通过分析位移阻抗,工程师可以更好地预测和优化系统的动态行为,确保其在各种工作条件下的稳定性和可靠性。
起重机的动刚度及其测试方法

3 起重机动刚度的测试方法
如前所述 ,起重机动刚度的测试 ,实际上就是测 试起重机在规定方向上的自振频率 。对于不同类型 的起重机 ,在不同方向上动刚度的大小 ,相应的标准
— 26 —
图 4 贴应变片法测试与分析框图 《起重运输机械》 1999 (4)
的动刚度 。这一方法的测试精度高于光线示波器 法 ;而采用动态数据采集分析系统则可直接对信号 进行采集和频谱或功率谱分析 ,实时地得到所测的 动刚度 ,具有速度快 、精度高的特点 。 3. 2 压电加速度计法
图 1 受简谐激振力的单自由度系统 图 2 单自由度系统的动刚度曲线
4 结束语
该微机监控系统在建设部长沙机械研究院设计 的 Q TZ2800 型塔式起重机上作了现场试验 ,结果证 明该微机电控系统工作稳定 、可靠 ,抗干扰能力强 , 功能强大 ,司机可以通过液晶屏随时掌握塔式起重 机的工作参数 ,起吊重物的自动就位误差小于 10cm ,各项功能达到了设计要求 。
λ= ω/ ωn ω ———简谐激振力角频率
动刚度的幅值为
| KD| = K (1 - λ2) 2 + (2ξλ) 2
(2)
可见 ,动刚度并非是一个常数 ,而是随频率的改
变而变化 ,是频率的函数 (见图 2) 。
1 动刚度的基本概念
在机械振动学中 ,动刚度的定义为起重机结构
产生单位振幅所需要的动态力 。对于受简谐激振力
的单自由度系统 (如图 1 所示) ,其动刚度 KD 可以 表示为 :
KD = K〔(1 - λ2) + 2 ξi λ〕
(1)
式中 K ———系统的静刚度
ξ———阻尼比
ξ= C/ (2 mωn) C ———阻尼系数
m ———系统质量 ωn ———系统固有频率 ωn = K/ m = 2πf n
机械结构的静态与动态刚度分析

机械结构的静态与动态刚度分析机械结构是由各种零部件组成的复杂系统,它承受着各种载荷和运动引起的力和变形。
在设计和优化机械结构时,静态和动态刚度分析是非常重要的工作。
本文将探讨机械结构的静态与动态刚度分析的基本概念和方法。
静态刚度分析是指在结构在静止状态下受到外力作用时的应力和变形的分析。
在实际工程中,我们通常关注结构的极限静态刚度,即结构在极限载荷下的最大应力和变形。
静态刚度分析可以通过有限元分析、解析方法以及试验等手段来进行。
有限元分析是一种常用的静态刚度分析方法。
它将结构离散成许多小单元,通过数值计算的方式求解结构的应力和变形。
有限元分析方法具有较高的精度和计算效率,可以用于复杂结构的分析和优化设计。
在有限元分析中,我们需要根据结构的几何形状和边界条件建立有限元模型,然后利用数学方程和力平衡定律求解结构的应力和变形。
解析方法是另一种常用的静态刚度分析方法。
它通过解析求解结构的应力和变形,适用于简单结构和简单载荷情况下的分析。
解析方法可以用于结构的初步设计和快速评估,但在复杂结构和非线性问题的分析中效果不佳。
试验是验证和验证静态刚度分析结果的关键手段。
在试验中,我们可以通过加载装置施加外力,并利用传感器测量结构的应力和变形。
试验可以考虑结构的材料非线性和几何非线性等因素,提供准确的静态刚度分析结果。
动态刚度分析是指结构在运动状态下受到外力时的应力和变形的分析。
在实际工程中,我们通常关注结构的共振频率和振型。
动态刚度分析可以通过模态分析和频响函数法等方法来进行。
模态分析是一种常用的动态刚度分析方法。
它通过求解结构的振动方程,得到结构的共振频率和振型。
在模态分析中,我们需要建立结构的数学模型,并求解特征值问题来获得结构的振动特性。
频响函数法是另一种常用的动态刚度分析方法。
它通过对结构施加调谐频率外力,并测量结构的响应,得到结构的频响函数。
频响函数可以用于评估结构在不同频率下的应力和变形。
总而言之,静态与动态刚度分析是机械结构设计与优化的重要环节。
原点动刚度
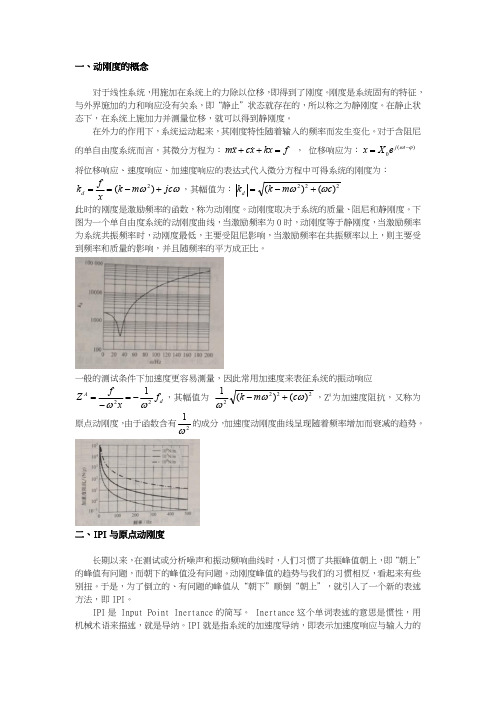
一、动刚度的概念对于线性系统,用施加在系统上的力除以位移,即得到了刚度。
刚度是系统固有的特征,与外界施加的力和响应没有关系,即“静止”状态就存在的,所以称之为静刚度。
在静止状态下,在系统上施加力并测量位移,就可以得到静刚度。
在外力的作用下,系统运动起来,其刚度特性随着输入的频率而发生变化。
对于含阻尼的单自由度系统而言,其微分方程为:f kx x c xm =++ ,位移响应为:)(0ϕω-=t j e X x 将位移响应、速度响应、加速度响应的表达式代入微分方程中可得系统的刚度为:ωωjc m k xf k d +-==)(2,其幅值为:222)()(c m k k d ωω+-=此时的刚度是激励频率的函数,称为动刚度。
动刚度取决于系统的质量、阻尼和静刚度。
下图为一个单自由度系统的动刚度曲线,当激励频率为0时,动刚度等于静刚度,当激励频率为系统共振频率时,动刚度最低,主要受阻尼影响,当激励频率在共振频率以上,则主要受到频率和质量的影响,并且随频率的平方成正比。
一般的测试条件下加速度更容易测量,因此常用加速度来表征系统的振动响应d A f x fZ 221ωω-=-=,其幅值为2222)()(1ωωωc m k +-,Z A 为加速度阻抗,又称为原点动刚度,由于函数含有21ω的成分,加速度动刚度曲线呈现随着频率增加而衰减的趋势。
二、IPI 与原点动刚度长期以来,在测试或分析噪声和振动频响曲线时,人们习惯了共振峰值朝上,即“朝上”的峰值有问题,而朝下的峰值没有问题。
动刚度峰值的趋势与我们的习惯相反,看起来有些别扭。
于是,为了倒立的、有问题的峰值从“朝下”顺倒“朝上”,就引入了一个新的表述方法,即IPI。
IPI 是Input Point Inertance 的简写。
Inertance 这个单词表述的意思是惯性,用机械术语来描述,就是导纳。
IPI 就是指系统的加速度导纳,即表示加速度响应与输入力的传递函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系统动刚度的概念 一个典型的由质量一弹簧一阻尼构成的机械系统的质量块在输入力f (t )作用下产生的输出位移为y (t ),其传递函数为 ()
()()1121/11222++=++==s s k k Ds ms s F s Y s G n n ωςω
系统的频率特性为
()()()n n j k j F j Y j G ωςωωωωωω21/122+⎪⎪⎭⎫ ⎝
⎛-== 该式反映了动态作用力f (t )与系统动态变形y (t )之间的关系,如图4-52所示。
图4-52 系统在力作用下产主变形
实质上()ωj G 表示的是机械结构的动柔度()ωλj ,也就是它的动刚度()ωj K 的倒数,即
()()()ωωλωj K j j G 1=
= () 当0=ω时
()()k j G j K ====001
ωωωω ()
即该机械结构的静刚度为k 。
当0≠ω时,我们可以写出动刚度()ωj K 的幅值
()k j K n n ⋅⎪⎪
⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-=2
222
21ωςωωωω () 其动刚度曲线如图4-53所示。
对()ωj K 求偏导等于零,即
()
0=∂∂ωωj K
可求出二阶系统的谐振频率,即
221ςωω-=n r ()
将其代入幅频特性,可求出谐振峰值
()212/1ςςω-==k
j G M r r
此时,动柔度最大,而动刚度()ωj K 具有最小值
()k j K ⋅-=2min 12ςςω ()
由式()和()可知,当1<<ς时,n r ωω→,系统的最小动刚度幅值近似为
()k j K ⋅≈ςω2min ()
由此可以看出,增加机械结构的阻尼比,能有效提高系统的动刚度。
上述有关频率特性、机械阻尼、动刚度等概念及其分析具有普遍意义,并在工程实践中得到了应用。
图4-53 动刚度曲线机械系统动刚
度的概念。
