结构化学 第六章
合集下载
结构化学课件第六章
显然,同前述结果一致
6.2 配体的群轨道
利用Oh群特征标表可知，
6L 6,0,0,2,2
A1g Eg T1u
令 x，y，z 正向的L是σ 1、σ 2、σ 3 ，负向为σ 4、σ 5、σ 6
A1g
1 6
1
2
3
4
5
6
Eg
1 2
1
4F 4Cl 4Br 4NH3 4F
为193，2F 227pm 为230，2Cl 295pm 为240，2Br 318pm 为207, 2NH3 262pm 为208， 2F 195pm
L'
L
L
Cu
L
L
L'
各种对称性场中 d 能级分裂
配
d d 位 场对称性
x2-y2
z2 dxy
dyz
dxz
注
数
2 直 线 形 - 0.628 3 正 三 角 形 0.545 4 正四面体形 - 0.267 4 平面正方形 1.228 6 正八面体形 0.600 5 三角双锥形 - 0.082 5 四 方 锥 形 0.914 7 五角双锥形 0.282
1.028 - 0.628 0.114 - 0.321 0.546 - 0.386 - 0.267 0.178 0.178 - 0.428 0.228 - 0.514 0.600 - 0.400 - 0.400 0.707 - 0.082 - 0.272 0.086 - 0.086 - 0.457 0.493 0.282 - 0.528
1
3
结构化学第六章..
二、d轨道的能级分裂
配体所形成的负电场对中心d电子起作用，消除d轨道的简并。
分裂的根源:(1)d轨道具有明显的角度分布。
(2)d轨道所在的配位场不是球形对称的。
1、正八面体配位场(Oh):
在正八面体配合物中，金属离子位于八面体中心，六 个配位体分别沿着三个坐标轴正负方向接近中央离子。
z y 3 2 4 5 6 1 x
四碘合汞（ll)酸 六氟合硅(IV)酸钾 二硫酸根合钴(II)酸钾 氯化二氨合银(I) 二水合一氯化二氯四氨合铬 (III) 三氯一氨合铂(II)酸钾 三氯五氨一水合钴(III) 四硫氰根· 二氨合铬(Ⅲ)酸铵
五、配合物和配体的分类
MLn 称单核配合物
中心原子(离子)M： MmLn 称多核配合物
M—M 称原子簇合物
配位数 5－－三角双锥或四方锥形
配位数 6－－八面体或三棱柱
表6.1
配位化合物 配位数 [Hg(NH3)2]2+ [Au(CN)2] [CuCN3]2Ni(CO)4 [Zn(NH3)4]2 [Ni(CN)4]2[PtCl4]2Os(CO)5
－
若干配位化合物所采取的几何构型
几何构型 直线型 直线型 平面三角形 四面体 四面体 平面正方形 平面正方形 三角双锥 对称性 配位化合物 配位数 几何构型 对称性 Dh Dh D3h Td Td D4h D4h D3h [Ni(CN)5]3[SbF5]2[CoF6]3- [Fe(CN)6]3Cr(CO)6 [ZrF7]3Re(S2C2Ph2)3 [Mo(CN)8]45 5 6 6 6 7 6 8 三角双锥 四方锥 八面体 八面体 八面体 五角双锥 三棱柱 十二面体 D3h C4v Oh Oh Oh D5h D3h D2d
结构化学第六章配位化合物结构
结构化学第六章配位化合物结构6001试述正八而体场中，中心离子d轨道的分裂方式6002试用分子轨逍理论阐明X , NH3和CN-的配体场强弱的次序。
6003按配位场理论，在Oh场中没有高低自旋络合物之分的组态是：----------- ()(A)d3 (B)d4 (C) d5 (D) d6 (E) d76004凡是中心离子电子组态为d6的八而体络合物，苴LFSE都是相等的，这一说法是否正确？6005络合物的中心离子的d轨道在正方形场中，将分裂成几个能级：-------------- ()(A) 2 (B)3 (C)4 (D)56006Fe(CN)63-的LFSE= ________________ 「6007凡是在弱场配位体作用下，中心离子d电子一立取高自旋态：凡是在强场配位体作用下，中心离子d电子一立取低自旋态。
这一结论是否正确？6008Fc(CN)6#中，CN-是强场配位体,FJ+的电子排布为心,故LFSE为________________ 。
6009尖晶石的一般表示式为AB2O4,其中氧离子为密堆积，当金属离子A占据正四而体门空隙时，称为正常尖晶石，而当A占据Oh空隙时，称为反尖晶石，试从晶体场稳左化能计算说明NiAl2O4晶体是什么型尖晶石结构(Ni?+为於结构)。
6010在Fe(CN)64-中的F2+离子半径比Fe(H2O)62+中的F2+离子半径大还是小？为什么？6011 作图证明CO是个强配位体。
6012CoFf啲成对能为21? 000cm1,分裂能为13? 000cnr1,试写出：(l)d电子排布⑵LFSE值(3)电子自旋角动捲⑷ 磁矩6013已知ML6络合物中(M%为的，＞1,尸20? 000 cm-1, P= 25? 000 cm1,它的LFSE 绝对值等于多少？ ----------------------- ()(A)0 (B) 25? 000 cnr1 (C) 54? 000 cnr1 (D) 8000 cnr16014四角方锥可认为是正八而体从z方向拉长，且下端没有配体L的情况。
结构化学第六章
第六章配位化合物的结构和性质
一．基本概念：
1．配合物、中心原子、配体、单核配合物、多核配合物
2．电价配合物、共价配合物、高自旋配合物和低自旋配合物
3．分子磁矩与未成对电子数的关系
4．晶体场、分裂能、成对能、光谱化学序、强场、弱场、晶体场稳定化能5．姜太勒效应和络合物畸变
6． M中σ型轨道和π型轨道
7． M-L之间的σ键及能级次序
8．羰基配合物中的σ-π键
9．π络合物中的σ-π键
10．电子规则和9n-l规则
二．基本计算和应用：
1．VBT与CFT理论对配合物的结构与性质的解释
2．d电子的排布、影响分裂能的因素
3．稳定化能的计算及应用
4．姜太勒效应
5．过渡金属络合物的颜色
6．络合物的几何构型
7．用分子轨道理论说明配合物的成键情况
8．σ-π型配键
三．重点内容
1．晶体场理论，d电子的排布、影响分裂能的因素，稳定化能的计算及应用2．配位场理论，八面体场的分裂，配位场稳定化能及对化合物性质的影响3．姜太勒效应
4．σ-π型配键及配位化合物的结构
四．自学引导
1．由静电作用模型引出晶体场理论，通过d电子轨道分裂引出分裂能、稳定化能及对配合物的结构与性质的解释
2．由分子轨道理论引出配位场理论，通过八面体场的分裂引出配位场稳定化能、姜太勒效应及对化合物性质的解释
3．通过σ-π型配键引出对过渡金属的配位化合物的结构、性质的解释。
五．作业
6.3，6.4，6.5，6.7，6.12，6.14，6.15，6.20， 6.23。
《结构化学第六章》
.
产生磁性的原因： 物质具有不同的磁性，首先是源于物质内部的电子组
态，即电子在原子轨道和分子轨道上的排布情况；其次是 源于化学成分、晶体结构、晶粒组织和内应力等因素，这 些因素引起磁矩排列的情况不同。
.
物质的磁结构分类:
.
6.6.2 顺磁共振
顺磁共振是研究具有未成对电子的物质，如配合物、 自由基和含有奇数电子的分子等顺次性物质结构的一种重 要方法，它又称为电子顺磁共振（EPR）或电子自旋共振 （ESR）。 原理：
.
三种成键方式（自由基反应）：
6.5.3 簇合物的催化性能（自学）
.
6.6 物质的磁性和磁共振
磁性是普遍存在的一种物质属性，任何一种物质材料 都有磁性，只不过表现形式和程度有所不同。物质的磁性 常用磁化率х或磁矩μ表示。磁化率是在外磁场H中物质 磁化强度M和磁场强度H的比值：
M/H
Χ是一个无量纲的量。
因子是为了使δ得到一个便于表达的数值。
对于扫频仪器，δ可以如下表达成
Δ是i 无量v纲 v参的，1由0于6 乘10v6因i v子参v，参所以1单0位6为ppm。
.
影响化学位移的因素： （1）核外电子分布 （2）抗磁各向异性效应 （3）溶剂效应和氢键的影响
.
3.磷、砷、锑、铋的三价化合物，如PF3、PCl3、AsCl3、 SbCl3、PR3等也可作为配位体形成σ—π配键。P、As等原子除 有一孤对电子可以作为电子对的供给者，与M形成σ键外，它还 有空的d轨道可和M形成反馈π键，使配位化合物稳定存在，例如 Pd(PF3)4、HCo(PF3)4、Ni(PF3)4、(R3P)4Mo(CO)2等。
.
6.3.2 不饱和烃配位化合物
以不饱和烃为配位体，通过σ—π配键与过渡金属形成的 配位化合物，在石油化工中占有重要地位。
产生磁性的原因： 物质具有不同的磁性，首先是源于物质内部的电子组
态，即电子在原子轨道和分子轨道上的排布情况；其次是 源于化学成分、晶体结构、晶粒组织和内应力等因素，这 些因素引起磁矩排列的情况不同。
.
物质的磁结构分类:
.
6.6.2 顺磁共振
顺磁共振是研究具有未成对电子的物质，如配合物、 自由基和含有奇数电子的分子等顺次性物质结构的一种重 要方法，它又称为电子顺磁共振（EPR）或电子自旋共振 （ESR）。 原理：
.
三种成键方式（自由基反应）：
6.5.3 簇合物的催化性能（自学）
.
6.6 物质的磁性和磁共振
磁性是普遍存在的一种物质属性，任何一种物质材料 都有磁性，只不过表现形式和程度有所不同。物质的磁性 常用磁化率х或磁矩μ表示。磁化率是在外磁场H中物质 磁化强度M和磁场强度H的比值：
M/H
Χ是一个无量纲的量。
因子是为了使δ得到一个便于表达的数值。
对于扫频仪器，δ可以如下表达成
Δ是i 无量v纲 v参的，1由0于6 乘10v6因i v子参v，参所以1单0位6为ppm。
.
影响化学位移的因素： （1）核外电子分布 （2）抗磁各向异性效应 （3）溶剂效应和氢键的影响
.
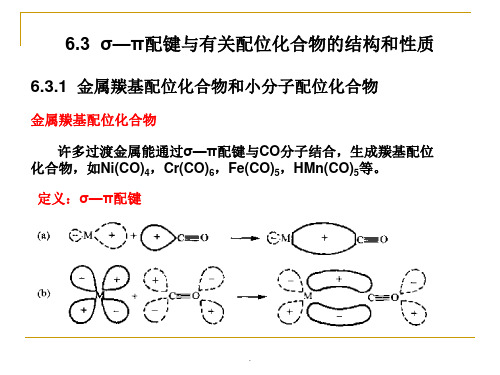
3.磷、砷、锑、铋的三价化合物，如PF3、PCl3、AsCl3、 SbCl3、PR3等也可作为配位体形成σ—π配键。P、As等原子除 有一孤对电子可以作为电子对的供给者，与M形成σ键外，它还 有空的d轨道可和M形成反馈π键，使配位化合物稳定存在，例如 Pd(PF3)4、HCo(PF3)4、Ni(PF3)4、(R3P)4Mo(CO)2等。
.
6.3.2 不饱和烃配位化合物
以不饱和烃为配位体，通过σ—π配键与过渡金属形成的 配位化合物，在石油化工中占有重要地位。
结构化学_第6章_5
↑↓ ↑
10 ↑↓ ↑↓ ↑↓
↑↓ ↑↓
-5P
↑↓ ↑↓ ↑↓
↑↓ ↑↓
LFSE
0 0.4Δo 0.8Δo 1.2Δo 1.6Δo-P 2.0Δo-2P 2.4Δo-3P 1.8Δo-3P 1.2Δo-3P 0.6Δo-3P -3P
表6.2.3 不同d电子组态的LFSE数值(Δo )
若不考虑成对能 ，即可定性解释有关规律(198)
主讲：
配合物中金属原子d电子填入分裂后的d轨道后，若不考 虑成对能，只考虑分裂能，则能量降低的总值称为配合 物稳定化能(LFSE）
主讲：
E (△o) 0.6 0.0 -0.4
弱场
d z2
dx2y2
高自旋配合物 [Fe(H2O)6]3+
[FeF6]3-
△0 < P
dxy
dxz
d yz
主讲：
E (△o) 0.6 0.0 -0.4
向于尽可能多地占据轨道，
形成HS型配位化合物
强配体场下，P < o，电子倾向
于尽可能少地占据轨道，形成
LS型配位化合物
主讲：
表6.2.3 不同d电子组态的能变 (p198)
dn
(HS)弱场
LS(强场)
t2g
e*g
LFSE
t2g
e*g
0
0
1↑
0.4Δo
↑
2 ↑↑
0.8Δo
↑↑
3 ↑↑↑
1.2Δo
↑↑↑
主讲：
6.2 配位场理论
6
主讲：
p197
6.2.3 配位场稳定化能与配合物性质
主讲：
0.6 E (△o)
0.0
《结构化学》第六章 金属的结构和性质
6.2 金属单质的晶体结构
金属单质晶体结构比较简单, 这与金属键密切相关: 由 于金属键没有方向性和饱和性，大多数金属元素按照等径 圆球密堆积的几何方式构成金属单质晶体，主要有立方面 心最密堆积、六方最密堆积和立方体心密堆积三种类型.
6.2.1 等径圆球最密堆积与A1、A3型结构
等径圆球以最密集的方式排成一列（密置列），进 而并置成一层（密置层），再叠成两层（密置双层）， 都只有一种方式：
非最密堆积方式中最重要的是立方体心堆积A2 , 还有A4和少数的A6、A7、A10、A11、A12等.
A2 立方体心密堆积
布鲁塞尔的原子球博物馆 9个直径18米的球形展厅构成一个立方体心模型
A4 金刚石型结构
A4中原子以四面体键相连. 晶胞中虽然都是同种原子， 但所处的环境不同(球棍图中用两色颜色来区分). 一个浅蓝 色球与一个深蓝色球共同构成一个结构基元.
A1最密堆积形成立方面心(cF)晶胞
ABCABC……堆积怎么会形成立方面心晶胞? 请来个逆向思维:
取一个立方面心晶胞：
体对角线垂直方向就是密置层, 将它们设成3种色彩:
从逆向思维你已明白， 立方面心晶胞确实满足 ABCABC……堆积。
那么, 再把思路正过来: ABCABC……堆积形成立 方面心晶胞也容易理解吧?
晶胞 六方P
四、 金刚石型晶体(A4型)
C原子的配位数为4， 2套等同点 结构基元：2个C 空间点阵型式：立方F 每个晶胞中有8个C原子， 其坐标分别为：
(0,0,0), (1/2,1/2,0),
(1/2,0,1/2),(0,1/2,1/2),
(1/4,1/4,1/4),(1/4,3/4,3/4),
(为看得清楚,绿 球和蓝球层各有3 个球未画出)
结构化学第6章
② 配位体群轨道 配体左手坐标，Z 指向中心原子，PZ—σ键， 由Oh 的简化群O 来作配位体的6个σ轨道—为Γ群
9
由此图决定 σ在 X , Y , Z 轴上，
3
x z y y
约化 群
4
z y x z y x
5
x
z
y
z
2
Г= A1 + E + T1 = A 1g + E g + T 1u
1
o M
n
Ln
19
12个配体π轨道组成 2T1 + 2T2 的基
T2g 的三基， dxy, dxz, dyz
y z z
x
y
x
3
配体
x
y
5
y
4
z
y z x
1
x
z yx
x z y
2
x
z
y z y 6
x
C3
12 ( x1+y2+x4 +y5 )
C4 , C 2
(x2+y3+y5+x 6)
20
21
T1u 的三基（Px, Py, Pz )
C O
如： d——p,
d——d,
d——π
18
当形成 d—p 时，共有 6 Px, 6Py ， 12个AO
O Г12π
E 12
6C4 0
3C42 -4
8C3 6C2’ 0 0 0
i
xn
yn
约化，
Г(O) = 2T1 + 2T2 Г(Oh) = T1u + T2u + T1g + T2g σπ 非键轨道 π
9
由此图决定 σ在 X , Y , Z 轴上，
3
x z y y
约化 群
4
z y x z y x
5
x
z
y
z
2
Г= A1 + E + T1 = A 1g + E g + T 1u
1
o M
n
Ln
19
12个配体π轨道组成 2T1 + 2T2 的基
T2g 的三基， dxy, dxz, dyz
y z z
x
y
x
3
配体
x
y
5
y
4
z
y z x
1
x
z yx
x z y
2
x
z
y z y 6
x
C3
12 ( x1+y2+x4 +y5 )
C4 , C 2
(x2+y3+y5+x 6)
20
21
T1u 的三基（Px, Py, Pz )
C O
如： d——p,
d——d,
d——π
18
当形成 d—p 时，共有 6 Px, 6Py ， 12个AO
O Г12π
E 12
6C4 0
3C42 -4
8C3 6C2’ 0 0 0
i
xn
yn
约化，
Г(O) = 2T1 + 2T2 Г(Oh) = T1u + T2u + T1g + T2g σπ 非键轨道 π
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单纯考虑配位原子或单原子配位体，则o随配位原子的原
子序数增大而减小：
C > N > O > F > S > Cl > Br > I ② 中心离子的影响 与离子的价态、所处的周期等因素有关。 Pt4+>Ir3+>Pd4+>Rh3+>Mo3+>Ru3+>Cr3+>Fe3+>V2+>Co2+>Ni2+>Mn2+
3. 分子轨道理论(Molecular Orbital Theory－MOT)
配位键的形成是由配体的相关轨道与中心离子（原子）价 轨道的线性组合而成。 中心金属原子轨道 ns, np, (n-1)d
cM M cL L
配位体群轨道: 根据配合物构型,由配体 的轨道组合成具有一定对称性的群轨道 MOT虽然可以得到较满意的结果，但处理过程过于冗长、
§6.3.2 八面体场的分裂能o
影响o的因素
① 配体的影响 CO ≈ CN– NO2– 邻蒽菲 联吡啶 SO32– 乙二胺(en) NH3 ≈ 吡啶 EDTA H2O C2O42– HCOO– ≈ OH– F– NCS– ≈ CI– Br– I– 称为光谱化学序列，由实验总结出的规律。 一般情况下，将在H2O以后(f<1.00)称为弱场配体， H2O以前(f > 1.00)称为强场配体。
第六章 配位化合物的结构和性质
§ 6.1 概述
含有中心金属原子(M)和若干配位体(L)的化合物称为配位 化合物(MLn)，简称配合物，又称络合物。 配位 离子 中心原子 (M): 含有d电子的过渡金属离子或原 子(具有空的价轨道) 配 位 键
分子或离子,带有负电荷或孤对 配体(L): 电子或键 单核配合物：一个中心原子
配合物的Jahn-Teller效应：
实验发现：配位数为 6的过渡金属配合物并非都是理想的
正八面体，有许多都是变形了的八面体。只有d 轨道的电 子呈球对称分布时，所形成的配合物才呈理想构型。 Jahn-Teller 在1937 年提出：在对称的非线性分子中，如 果体系的基态有几个简并态，则体系是不稳定的，体系
§6.2.1 晶体场理论的基本观点
中心离子和配体间的作用为静电作用 (类似于晶体中的正 负离子间的作用) 中心离子d 轨道在周围配位体影响下能级发生分裂。
§6.2.2 晶体场中d 轨道能级的分裂
1. 正八面体场(Oh)中的d轨道能级分裂
d 轨道分裂成两组：一组是能量较高的 dz2 和 dx2-y2 (二重 简并)，另一组是能量较低的 dxy、dxz、dyz (三重简并)。 在正八面体 Oh 群中，dx2-y2, dz2 同属 eg 不可约表示 (e 表示 二重简并，g 中心对称)。dxy、dyz、dxz 同属 t2g 不可约表示
(1) 电价配键与电价络合物 带正电的中心离子与带负电或有偶极矩的配体之间靠静电 引力结合，称电价配键。 例如：[FeF6]3-、［Fe(H2O)6］2+、[Ni(NH3)6]2+ 在形成络合物前后，自旋未成对电子数不变
(2) 共价配键和共价络合物 中心离子以空的价轨道(杂化轨道)接受配位体的孤对电子
八面体配位场中的分裂能
a1g ns t2 g eg
0
e
* g
Ee* Et2 g 0 10 Dq
g
t2 g
t1u a1g
eg
6 a1g t1u eg
Dq为一种能量单位
配位化合物的分子轨道能级图
中心离子的d电子就填充在 t2g与eg*上，排布方式取决于
分裂能 O与电子成对能 P 的相对大小。配合物的很多性 质 ( 磁性，光谱，热力学及稳定性等 ) 都取决于这两个轨 道上电子排布的状况。
0 3 6 *2 10 d , d , t e , d 2g g 3 *2 6 t e ( HS ), t 2 g ( LS ) 2g g
理想八面体
大畸 变
变形八面体
3 *1 6 *3 6 *1 t e ( HS ), t 2 g eg , t2 g eg ( LS ) 2g g 1 2 4 *2 5 *2 5 t2 g , t2 g , t2 g eg ( HS ), t2 g eg ( HS ), t2 g
型：dxy dyz dxz ……t2g
Oh群的不可约表示
② 配位体群轨道 6 个 L ：每个至少有 1
个 型轨道，共有 6个
轨道 ( 一般是配体孤对 电子轨道 ) 。将这 6 个
轨道重新组合成新的
群轨道，使之与M的原 子轨道对称性匹配。
配位体群轨道及其对称性
a1g
1 ( 1 2 3 4 5 6 ) 6
多核配合物：两个或以上中心原子
配位化合物的磁性
有未成对电子 顺磁性
ge s(s 1)e
n(n 2)e
[Fe(H2O)6]2+ [Fe(CN)6]4实验磁矩
=5.3B =0
n=4 n=0
高自旋 低自旋 配合物结构
未成对电子数
§6.1.3 配位化合物的化学键理论
1. 价键理论(Valence Bond Theory－VBT)
组态
d1 d2 d3 d4 d5 d6 d7
排布
t2g1 t2g2 t2g3 t2g3eg1 t2g3eg2 t2g4eg2 t2g5eg2
未成对 电子数
1 2 3 4 5 4 3
LFSE
4Dq 8Dq 12Dq 6Dq 0Dq 4Dq 8Dq
排布
t2g1 t2g2 t2g3 t2g4 t2g5 t2g6 t2g6eg1
把中心离子与配位体的相互作用，看作类似于晶体中正负 离子间的相互作用。着眼点是中心离子 d 轨道在周围配位
体影响下的能级发生分裂。
电子在分裂了的轨道上的排布状态，决定了配位场的光谱、 磁性、稳定性、几何构型等性质。CFT 可比较满意地解释
上述性质。但这个理论没有考虑中心离子与配体间的共价
作用成份，不能解释羰基、不饱和烯等配合物的成键本质。
t=4O/9 t2- e=4/910Dq 2e+ 3t2=0 t2= 2t /5=1.78Dq e= -3t /5 =-2.76Dq
t2 g
dxy,dyz,dxz
eg
b1g d x 2 y2
b2 g
dxy
t2
d xy ,d yx ,d yz
dx2-y2,dz2
e
eg
dx2-y2,dz2
一定要发生畸变，以消除这种简并，从而处于更稳定的
状态。 通俗地讲：如果d 电子在eg*和 t2g 轨道上呈不均匀分布时， 则配合物的构型要偏离理想构型，产生长、短键之分。这
是 Jahn-Teller 效应。
Cu2+：d 9，八面体场时，d 电子有两种排布
dz2 dx2-y2
(t2 g ) 6 ( d z 2 ) 2 ( 数
1 2 3 2 1 0 1
LFSE
4Dq 8Dq 12Dq 16Dq-P 20Dq-2P 24Dq-2P 18Dq-P
d8 d9 d10
t2g6eg2 t2g6eg3 t2g6eg4
2 1 0
12Dq 6Dq 0Dq
t2g6eg2 t2g6eg3 t2g6eg4
2 1 0
12Dq 6Dq 0Dq
§6.3.3 配位场稳定化能
(I) 配位场稳定化能(LFSE) 晶体场稳定化能(CFSE)
d 电子在分裂前 d 轨道中总能量(ETS)与在分裂后 d 轨道中 的总能量(ETLF)之差。
LFSE = ETS － ETLF= － ETLF
一般选 d 轨道分裂前 d 电子的总能量为零点，则 LFSE 就 表示 d 电子轨道分裂后的总能量的负值。LFSE 越大，配 合物越稳定。
t2 g
dxy,dyz,dxz
a1g
dz2
d x 2 -y2 ,d z2
eg
d xz ,d yz
ML8
ML4
M
ML6
ML4L2'
ML4
立方体场
四面体场
球形场 八面体场 拉长八面体场 平面四方 形场
各种配位场中金属d轨道能级的分裂情况
§6.3 配位场理论
§6.3.1 ML6八面体配位化合物的分子轨道
20 世纪 30 年代初由 Pauling 等人提出。它的基本思想是 中心离子的杂化轨道与配位体孤对电子形成配位键。 中心离子采用什么样的杂化轨道，取决于中心离子的 电子构型和配体的性质。VBT能解释配合物的配位数、几 何构型、磁性等性质。但它是个定性理论，不涉及轨道能 级等概念，所以不能解释配合物的紫外 - 可见光谱等性质， 对光谱化学序列也无法给出合理的解释。
两长四短键
dxy dxz dyz
能量简并
dz2 dx2-y2
(t2 g ) 6 ( d z 2 )1 ( d x2 y 2 ) 2
两短四长键
dxy dxz dyz
拉长八面体
压扁八面体
较低能级(t2g)上d 电子排布不均匀时，发生小畸变。 较高能级(eg*)上d 电子排布不均匀时，发生大畸变。
设M位于直角坐标系原点， 6个 L 位于坐标轴上。M共有9个价轨道 可参与分别形成或型分子轨道： 型： s px py
pz dx2-y2 dz2
型：dxy dyz dxz
① 中心原子AO对称性分类 型： s ……………..a1g
px py pz ……t1u
dx2-y2 dz2 ………eg
例2：[Co(NH3)6]3+, Co3+: d 6, O=23000 cm-1, P=21000 cm-1