2014年秋季班数学八年级讲义(8)
秋季初二数学经典讲义(根式、勾股定理、轴对称)

第一章二次根式______________________________________________________________ 2一、基础知识_____________________________________________________________ 2二、精讲精炼_____________________________________________________________ 3 第二章勾股定理_____________________________________________________________ 20一、基础知识____________________________________________________________ 20二、精讲精练____________________________________________________________ 21 第三章直角三角形___________________________________________________________ 40一、基础知识____________________________________________________________ 40二、精讲精练____________________________________________________________ 41 第四章轴对称_______________________________________________________________ 48一、基础知识____________________________________________________________ 48二、精讲精练____________________________________________________________ 49第一章二次根式一、基础知识二、精讲精炼一、基础定义1.如果x 的平方等于a ,那么x 就是a 的 ,所以的a 平方根是2.非负数a 的平方根表示为3.因为没有什么数的平方会等于 ,所以负数没有平方根,因此被开方数一定是 或者4的平方根是 5.非负的平方根叫 平方根 6. 9的算术平方根是( )A .-3B .3C .±3D .81 8.下列说法中正确的是( )A .9的平方根是3B 22 9. 64的平方根是( )A .±8B .±4C .±2D 10. 4的平方的倒数的算术平方根是( ) A .4 B .18 C .-14 D .1414.一个自然数的算术平方根是x ,则它后面一个数的算术平方根是( )A .x+1B .x2+1 C15.若2m-4与3m-1是同一个数的平方根,则m 的值是( )A .-3B .1C .-3或1D .-1 1、25的平方根是( )A 、5B 、5-C 、5±D 、5±2.36的平方根是( )A 、6B 、6±C 、6 D 、 6±3.当≥m 0时,m 表示( )A .m 的平方根B .一个有理数C .m 的算术平方根D .一个正数 5.算术平方根等于它本身的数是( )A 、 1和0B 、0C 、1D 、 1±和0 6.0196.0的算术平方根是( )A 、14.0B 、014.0C 、14.0±D 、014.0± 7.2)6(-的平方根是( )A 、-6B 、36C 、±6D 、±6 20.2)5(-的平方根是( )A 、 5±B 、 5C 、5-D 、5±24.已知一个正方形的边长为a ,面积为S ,则( ) A .a S =B.S 的平方根是aC.a 是S 的算术平方根D.S a ±=27.22)4(+x 的算术平方根是( )A 、 42)4(+x B 、22)4(+x C 、42+x D 、42+x28.一个自然数的算术平方根是a ,则下一个自然数的算术平方根是( ) A .()1+a B .()1+±a C .12+a D .12+±a29.3612892=x ,那么x 的值为( ) A .1917±=xB .1917=xC .1817=xD .1817±=x 30.2)8(-= , 2)8(= 。
初二数学(秋季)讲义第8讲 平面直角坐标系

初二数学(秋季)讲义 第八讲 平面直角坐标系导入在电影票上,“3排6座”与“6排3座”______(填“是”或“不是”)同一个座位,所以在电影院选择座位需要____个数据.1. 如图,在数轴上有A ,B ,C ,D 四个点,回答下列问题(1)点C 关于点A 的对称点表示的数是______;点D 关于点B 的对称点表示的数是______.(2)点C 向右平移3个单位后表示的数是______;点B 向左平移2个单位后表示的数是______.(3)点A 关于点B 的对称点向左平移2个单位后表示的数 是_______.2. 如图是某市的部分简图,每个小正方形的边长均为500米,我们用(2,6)表示文化宫的位置,请回答下列问题:东北(1)说出体育场与超市的位置;(2)小明家在火车站以东1 000米,再往北500米处;小聪家在超市以北500米,再往西1 500米处,在图中标出小明和小聪家的位置.(3)上周六,小华的活动路线是(1,8)→(2,6)→(7,7)→(7,2),说一说他这一天去了哪些地方. 1. 在平面内,确定一个物体的位置一般需要____个数据.2. 在平面内,两条__________且有_________的_________组成平面直角坐标系.水平的数轴叫_______或_______,铅直的数轴叫________或_______,________和______统称坐标轴.3.如图,对于平面内任意一点P,过点P分别向x轴、y轴________,垂足在x轴、y轴上对应的数a,b分别叫做点P的_______、_______,__________(a,b)叫做点P的坐标.)4.坐标系把平面分成了_____个象限,第一象限内点的坐标特征是(+,+),第二象限内点的坐标特征是__________,第三象限内点的坐标特征是__________,第四象限内点的坐标特征是_________;坐标轴上的点不属于任何象限.5.在直角坐标系中,对于平面上的任意一点,都有唯一的一对有序实数对(即点的坐标)与它对应;反过来,对于任意一对有序实数对,都有平面上唯一的一点和它对应.6.坐标特点(1)x轴上的点____坐标等于零;y轴上的点____坐标等于零.(2)平行于x轴的直线上的点____坐标相同;平行于y轴的直线上的点____坐标相同.(3)关于x轴对称的两个点,横坐标_____,纵坐标______;关于y轴对称的两个点,横坐标________,纵坐标_____.(4)横坐标加减管______平移,纵坐标加减管______平移.1.写出图中的多边形ABCDEF各个顶点的坐标,并指出它们所在的象限.解:A(___,___),第___象限;B(___,___),第___象限;C(___,___),第___象限;D(___,___),第___象限;E( ),______象限;F( ),______象限.2.在平面直角坐标系中,点(-2,-3)在第____象限;点在第____象限;点1,1在第___象限;点(-2,a2+1)在第___马帅炮兵3. 若a <b <0,则点A (a -b ,b )在第________象限.4. 在平面直角坐标系中,若点P (a ,b )在第二象限,则点Q (1-a ,-b )在第____象限.5. 在平面直角坐标系中描出下列各点,并将各组内这些点依次用线段连接起来. (1)A (-3,5),B (-7,3),C (1,3),A (-3,5); (2)D (-6,3),E (-6,0),F (0,0),G (0,3).观察所描出的图形,解答下列问题:①坐标轴上的点有_______________,且x 轴上的点___坐标等于零,y 轴上的点___坐标等于零.②线段BC 与x 轴_______,点B 和点C ____坐标相同,线段BC 上其他点的____坐标都相同.③线段DE 与y 轴________,点D 和点E ____坐标相同,线段DE 上其他点的____坐标都相同.6. 若点M (a +3,4-a )在x 轴上,则点M 的坐标为__________.7. 若过A (4,m ),B (n ,-3)两点的直线与x 轴平行,且AB =5,则m =_____,n =_______________.8. 如图,正方形ABCD 在平面直角坐标系中,其中三个顶点的坐标分别为(-2,-2),(-2,3),(3,-2),则第四个顶点的坐标为________.第9题图9. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点(___,___).10. 已知点P (-3,2),它到x 轴的距离为_____,到y 轴的距离为_____,到原点的距离为_____.11. 如图,长方形ABCD 的长与宽分别是6,4,建立适当的平面直角坐标系,并写出各个顶点的坐标.D CBA12. 如图,对于边长为4的等边三角形ABC ,建立适当的平面直角坐标系,写出各个顶点的坐标.A C13. 在平面直角坐标系中,第二象限内有一点P ,若点P 到x 轴的距离是4,到y 轴的距离是5,则点P 的坐标为________.14. 点M 在x 轴的上方,距离x 轴4个单位长度,距离y 轴3个单位长度,则点M 的坐标为( )A .(4,3)B .(-4,3)或(4,3)C .(3,4)D .(-3,4)或(3,4)15. 若点A (x ,4)到原点的距离为5,则x =____________.16.如图,△ABC在平面直角坐标系中,则S△ABC=________.17.已知点A(0,4),点B在x轴上,若AB与坐标轴围成的三角形的面积为2,则点B的坐标为______________.18.(1)作图,将△ABC各顶点的横坐标保持不变,纵坐标乘以-1,顺次连接这些点,所得三角形与△ABC关于_____轴对称;(2)如图,△DEF与△ABC关于____轴对称,它们相应顶点的横坐标___________、纵坐标____________.19.如果点A(a,b)与点B关于x轴对称,点B与点C(2,3)关于y轴对称,那么a=_______,b=_______,点A和点C的位置关系是__________________.20.若点A(a,4),点B(3,b)关于x轴对称,则(a+b)2 015的值为______.21.若点P(b-3,-2b)在y轴上,则点P关于x轴对称的点的坐标为__________.22.若点A(a,b)沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度得到点A′(1,2),则点A的坐标为_______.23.如图,将三角形向右平移3个单位长度,再向上平移2个单位长度,则平移后三个顶点的坐标分别为()A.(-1,-1),(2,3),(5,1)B.(-1,1),(3,2),(5,1)C.(-1,1),(2,3),(5,1)D.(1,-1),(2,2),(5,1)24.如图,把图1中的△ABC经过一定的变换得到图2中的△A′B′C′,如果图1中△ABC上点P的坐标为(a,b),那么这个点在图2中的对应点P′的坐标为______________.图1图21.不是,两2.(1)0,-2;(2)-1,-1;(3)23.(1)体育场(1,8);超市(7,2)(2)略(3)他这一天去的地方:体育场、文化宫、宾馆、超市1.两2.互相垂直,公共原点,数轴x轴,横轴,y轴,纵轴,x轴,y轴3.作垂线,横坐标,纵坐标,有序实数对4.四,(-,+),(-,-),(+,-)6.(1)纵,横(2)纵,横(3)相同,互为相反数,互为相反数,相同(4)左右,上下1.(-1,3),二;(-2,-1),三;(-1,-2),三;(3,-2),四(3,1),第一;(2,3),第一2.三,一,四,二3.三4.四5.图形略①E,F,G;纵;横②平行,纵,纵③平行,横,横6.(7,0)7.-3,-1或98.(3,3)9.(-3,1)10.2,311.略12.略13.(-5,4)14.D15.3或-316.917.(1,0)或(-1,0)18.(1)x;(2)y,互为相反数,相同19.-2,-3,关于原点中心对称20.-121.(0,6)22.(-2,0)23.A24.(a+3,b+2)。
2014年秋季班数学八年级讲义(5)
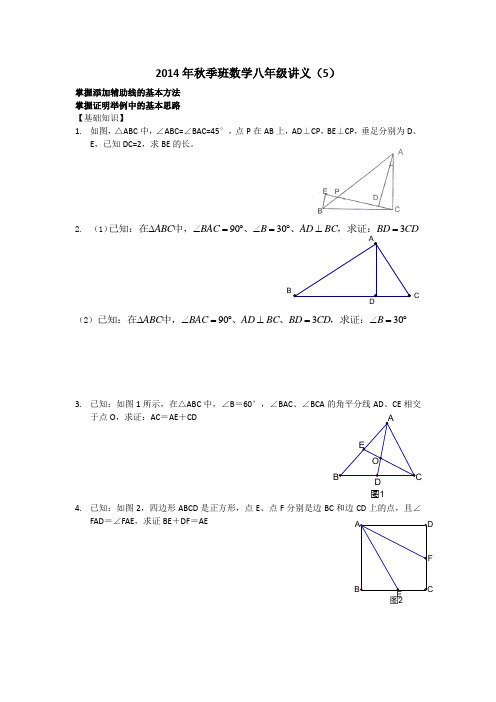
图1DC图22014年秋季班数学八年级讲义(5)掌握添加辅助线的基本方法 掌握证明举例中的基本思路 【基础知识】 1. 如图,△ABC 中,∠ABC=∠BAC=45°,点P 在AB 上,AD ⊥CP ,BE ⊥CP ,垂足分别为D 、E ,已知DC=2,求BE 的长。
2. (1)90303ABC BAC B AD BC BD CD ∆∠=︒∠=︒⊥=已知:在中,、、,求证:(2)90330ABC BAC AD BC BD CD B ∆∠=︒⊥=∠=︒已知:在中,、、,求证:3. 已知:如图1所示,在△ABC 中,∠B =60°,∠BAC 、∠BCA 的角平分线AD 、CE 相交于点O ,求证:AC =AE +CD4. 已知:如图2,四边形ABCD 是正方形,点E 、点F 分别是边BC 和边CD上的点,且∠FAD =∠FAE ,求证BE +DF =AECD5. 已知:如图,在四边形ABCD 中, AB =CD ,点E 、F 分别是边AB 、CD 的中点,DE =BF .求证:∠A =∠C .6. 求证:在两个锐角三角形中,如果有两边及其中一边上的高对应相等,那么这两个三角形全等。
(画图、写出已知、求证和证明)【提高练习】1. 如图,在△ABC 中,∠BAC 、∠BCA 的平分线相交于点I ,若∠B =35°,BC =AI +AC ,求∠BAC 的度数2. 如图,在正方形ABCD 中,点E 、F 分别在BC 、CD 上移动,但A 到EF 的距离AH 始终保持与AB 长相等,问在E 、F 移动过程中: (1)求证:∠EAF =45o(2)△ECF 的周长是否有变化?请说明理由3. ,120ABC AB AC BAC ∆=∠=︒已知:在中,(1)2D BC DE AB DF AC DE DF BC D BC DE AB DF AC DE DF BC ⊥⊥⊥⊥是上的一动点,,,你能发现、、之间的数量关系吗?()是直线上的一动点,直线,直线,试探究线段、之间的数量关系。
精品2014年八年级数学上册-三角形初步认识同步讲义+练习

精品2014年⼋年级数学上册-三⾓形初步认识同步讲义+练习三⾓形初步认识第01课与三⾓形有关的线段知识点:三⾓形定义:组成的图形叫做三⾓形。
⽤符号“△”表⽰。
注意:三条线段必须①;②组成三⾓形的线段叫做三⾓形的,相邻两边所组成的⾓叫做三⾓形的,简称⾓,相邻两边的公共端点是三⾓形的。
注意:三⾓形ABC 的顶点C 所对的边AB 可⽤c 表⽰,顶点B 所对的边AC 可⽤b 表⽰,顶点A 所对的边BC 可⽤a 表⽰.三⾓形三要素:、、。
三⾓形三边的不等关系:。
附加:公式:三⾓形的分类:(1)按⾓分类: 三⾓形、三⾓形、三⾓形。
(2)按边分类:三⾓形的⾼线:从三⾓形的⼀个向它的对边所在直线作,顶点和垂⾜之间的叫做三⾓形的⾼线,简称三⾓形的⾼.注意:⾼与垂线不同,⾼是线段,垂线是直线。
三⾓形的三条⾼,简称三⾓形的⼼。
三⾓形的中线:如图,我们把连结△ABC 的顶点A 和它的对边BC 的中点D ,所得线段AD 叫做△ABC 的钝⾓三⾓形直⾓三⾓形锐⾓三⾓形位置边BC 上的中线,表⽰为BD=DC 或BD=DC=21BC 或2BD=2DC=BC. 三⾓的三条中线,简称三⾓形的⼼。
注意:三⾓形的中线是线段。
三⾓形的⾓平分线:如图,画∠A 的平分线AD ,交∠A 所对的边BC 于点D ,所得线段AD 叫做△ABC 的⾓平分线,表⽰为∠BAD=∠CAD 或∠BAD=∠CAD =1/2∠BAC 或2∠BAD=2∠CAD =∠BAC 。
三⾓形三个⾓的平分线,简称三⾓形的⼼。
注意:三⾓形的⾓平分线是线段,⽽⾓的平分线是射线,是不⼀样的。
三⾓形稳定性(1)把三根⽊条⽤钉⼦钉成⼀个三⾓形⽊架,然后扭动它,它的形状会改变吗? (2)把四根⽊条⽤钉⼦钉成⼀个四边形⽊架,然后扭动它,它的形状会改变吗? (3)在四边形的⽊架上再钉⼀根⽊条,将它的⼀对顶点连接起来,然后扭动它,它的形状会改变吗?例1.⽤⼀条长为18cm 的细绳围成⼀个等腰三⾓形. (1)如果腰长是底边的2倍,那么各边的长是多少? (2)能围成有⼀边长为4㎝的等腰三⾓形吗?为什么?例2.已知△ABC 的周长是24cm ,三边a 、b 、c 满⾜c+a=2b ,c-a=4cm ,求a 、b 、c 的长.三⾓形中线的性质:例3.⼀个等腰三⾓形的周长为32 cm,腰长的3倍⽐底边长的2倍多6 cm.求各边长.例4.如图,在直⾓三⾓形ABC中,∠ACB=900,CD是AB边上的⾼,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的⾯积;(2)CD的长;(3)作出△ABC的边AC上的中线BE,并求出△ABE的⾯积;(4)作出△BCD的边BC边上的⾼DF,当BD=11cm 时,试求出DF的长。
2014年秋季班数学八年级讲义(9)

2014年秋季班数学八年级讲义(9)直角三角形中两锐角互余;直角三角形斜边上的中线等于斜边的一半;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°【基础知识】1. 如果三角形中有一条边是另一条边是2倍,并且有一个角是30°,那么这个三角形是( )(A )直角三角形 (B )锐角三角形 (C )钝角三角形 (D )图形不能确定2. 在直角三角形中,两锐角的平分线相交成钝角的度数是_______°3. 已知,Rt △ABC 中,∠ACB =90°,AB =8cm ,D 为AB 中点,DE ⊥AC 于E ,∠A =30°,求BC ,CD 和DE 的长。
4. 已知:△ABC 中,AB =AC =BC ,D 为BC 边上的中点,DE ⊥AC 于E.求证:14CE AB【提高练习】1. 如图所示,BD 、CE 是三角形ABC 的两条高,M 、N 分别是BC 、DE 的中点求证:MN ⊥DE 。
2. 已知:如图AD ∥BC ,且BD ⊥CD ,BD =CD ,AC =BC ,求证:AB =BO.3. 如图,在ΔABC 中,∠B =40°,∠C =20°,AD ⊥CA 于A ,交BC 于D ,求证:CD =2AB4. 如图,AB ∥CD ,E 是AD 中点,CF ⊥AB 于F 。
求证:CE =EF5. 如图,在ΔABC 中,∠ABC =2∠C ,AD ⊥BC 于D ,E 是AC 中点,ED 的延长线与AB 的延长线交于点F ,求证:BF =BD6. 在等边三角形ABC 中,点D 、E 分别在AB 、AC 边上,AD=CE ,CD 与BE 交与F,DG ⊥BE 。
求证:(1)BE=CD;(2)DF=2GF7. 在等边ΔABC 中,AE=CD ,BG ⊥AD ,求证:BP=2PG8. 在△ABC 中,AB =AC ,∠A =120°,AB 的中垂线交AB 于D ,交CA 延长线于E ,求证:BC 21DE 。
2014年秋季班数学八年级讲义(10)

2014年秋季班数学八年级讲义(10)勾股定理:直角三角形两直角边的平方和等于斜边的平方。
也就是说:如果直角三角形的两直角边为a 、b ,斜边为c ,那么222a b c +=。
公式的变形:222a c b =-或222b c a =-。
勾股定理的逆定理:如果三角形ABC 的三边长分别是a ,b ,c ,且满足222a b c +=,那么△ABC 是以∠C 为直角的直角三角形。
勾股数:满足222a b c +=的三个正整数,称为勾股数。
一组勾股数扩大相同的正整数倍后,仍是勾股数。
常见勾股数有:(3,4,5)、(5,12,13)、(7,24,25)、(8,15,17) 【基础知识】1. 已知直角三角形中30°角所对的直角边长是32cm ,则另一条直角边的长是( ) A .4cm B .34cm C .6cm D .36cm2. △ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为( ) A .42 B .32 C .42或32 D .37或333. 一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动( )A . 9分米B .15分米C .5分米D .8分米 4. 一架方梯长25米,如图,斜靠在一面墙上,梯子底端离墙7米,(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?(3)当梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等时,这时梯子的顶端距地面有多高?【提高练习】 1. 小明的叔叔家承包了一个矩形鱼池,已知其面积为48m 2,其对角线长为10m ,为建栅栏,要计算这个矩形鱼池的周长,你能帮助小明算一算吗?2. 如图,铁路上A ,B 两点相距25km ,C ,D 为两村庄,DA ⊥AB 于A ,CB ⊥AB 于B ,已知DA=15km ,CB=10km ,现在要在铁路AB 上建一个土特产品收购站E ,使得C ,D 两村到E站的距离相等,则E 站应建在离A 站多少km 处?A A ′ A ′ O A D EB C第22题图B A6cm 3cm 1cm3. 已知,△ABC 中,AB=17cm ,BC=16cm ,BC 边上的中线AD=15cm ,试说明△ABC 是等腰三角形。
【初二数学上册(秋季班)讲义】第08讲_平面直角坐标系的应用(学生版)A4
高斯初二数学八年级上册秋季班(学生版)最新讲义初二数学八年级上册秋季班辅导讲义学员姓名:刘小米年级:辅导科目:小学思维学科教师:五块石1 上课时间2020-06-25 14:00-16:00授课主题第02讲_平面直角坐标系的应用平面直角坐标系的应用一.坐标系内图形的变换图形的平移1.在平面直角坐标系中,图形上各点的纵坐标不变,横坐标分别加上(或减去)一个正数a,则图形沿水平方向向右(或向左)平移a个单位长度,图形形状、大小不变.2.在平面直角坐标系中,图形上各点的横坐标不变,纵坐标分别加上(或减去)一个正数b,则图形向上(或向下)平移b个单位长度,图形形状、大小不变.二.计算坐标系内图形面积常用“割补法”.割:分割,把图形分割成几部分容易求解的图形,分别求解,然后相加即可.补:补齐,把图形补成一个容易求解的图形,然后再减去补上的那些部分.知识图谱错题回顾知识精讲一.考点:用坐标表示地理位置,坐标系内图形的变换,计算坐标系内图形的面积,坐标找规律.二.重难点:坐标系内图形的变换,计算坐标系内图形的面积,坐标找规律.三.易错点:1.平行移动最关键的是掌握平移的方向与坐标变化之间的关系,可以用口诀形式表示: 横坐标,右移加,左移减;纵坐标,上移加,下移减;2.求面积时,优先考虑补的方法,通常补成一个长方形或者梯形,之后再相减求解即可;3.计算坐标系内图形的面积时,平行或垂直于坐标轴直线上的两个点之间的距离,用横坐标之差的绝对值或者纵坐标之差的绝对值表示.题模一:用坐标表示地理位置例1.1.1如图是我市几个旅游景点的大致位置示意图,如果用(0,0)表示新宁莨山的位置,用(1,5)表示隆回花瑶的位置,那么城市南山的位置可以表示为( )A .(2,1)B .(0,1)C .(-2,-1)D .(-2,1)题模二:坐标系内图形的变换例1.2.1已知点P 1(a-1,4)和P 2(2,b )关于x 轴对称,则(a+b )2013的值为( ) A .-1 B .0C .1D .(-3)2013例1.2.2点A 在平面直角坐标系xOy 中的坐标为()2,5,将坐标系xOy 中的x 轴向上平移2个单位,y 轴向左平移3单位,得到平面直角坐标系xOy ,在新坐标系xOy 中,点A 的坐标为________例1.2.3已知A B C ∆'''是由ABC ∆经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:(1)观察表中各对应点坐标的变化,并填空: a =_____,b =_____,c =_____;三点剖析题模精讲(2)在平面直角坐标系中画出ABC ∆及平移后的A B C ∆'''; (3)直接写出A B C ∆'''的面积是_____。
精品 2014年八年级数学上册暑期讲义+同步练习

整式的乘除与因式分解第一课 积的乘方 幂的乘方知识点:1.同底数幂的乘法: 公式:2.幂的乘方:公式:3.积的乘方:公式:同底数幂基础练习:(1)()())(222222222243=⨯⨯⨯⨯⨯⨯=⨯ (2)35 ⨯45= )(5=(3)7)3(-⨯6)3(-= ())(3-= (4))(⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⨯⎪⎭⎫ ⎝⎛1011011013(5)3a ⨯4a = =()a 幂的乘方基础练习:(1)23)2(= = =)(2; (2)54)(x = = =)(x;(3)3100)3(= = =)(3 ;(4)23])2[(-= = =)()2(-=)(2;积的乘方基础练习:(1)3)2(x = = × = (2)4)3-(x = = × = (3)5)(ab = = × =例1.计算:(1)310⨯410= ;(2)53a a a ⋅⋅= ;(3);(4)x x x x ⋅+⋅22=(5)11010+⋅m n = ; (6);97)(m m m ⋅-⋅= ;(7)()3922-⨯= ; (8)y y y y ⋅-⋅⋅-425)(=(9)103=)(233⋅=)(533⋅=)(733⋅例2.把下列各式化成()ny x +或()ny x -的形式.(1) ()()43y x y x ++ = ; (2)()()()x y y x y x ---23= ;(3)()()12+++m my x y x = ; (4)342)()()(y x x y y x --- = ;(5)23)()(y x y x +-- = ;例3.计算:(1)32)2(= (2)34)3(= (3)65)(x = (4)3)(n x = (5)8x =)(2)(x =)(xx ⋅2=)(xx ⋅3 (6)12x =)(2)(x =)(xx ⋅2=)(xx ⋅7=)(3)(x例4.计算:(1)()332⨯; (2)()253⨯; (3)()22ab ; (4)()432a ;(5)10001001)21()2(-⨯- (6)()23351021104⎪⎭⎫ ⎝⎛⨯-⨯⨯ (7)20019911323235.0⎪⎭⎫ ⎝⎛⨯-⋅⎪⎭⎫ ⎝⎛⨯例5.已知:2,3==n m x x ,求n m x 23+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年秋季班数学八年级讲义(8)
掌握直角三角形全等的判定定理:斜边、直角边公理:斜边和一条直角边对应相等的两个直角三角形全等(H.L.)
【基础知识】
1.判断下列条件能否判断两直角三角形全等,并说明理由
(1)一个锐角和这个锐角的对边对应相等。
(2)一个锐角和这个锐角相邻的一条直角边对应相等。
(3)一锐角与斜边对应相等。
(4)两直角边对应相等。
(5)两边对应相等。
(6)两锐角对应相等。
(7)一锐角和一边对应相等
2.下面说法不正确的是()
A、有一角和一边对应相等的两个直角三角形全
B、有两边对应相等的两个直角三角形全等
C、有两角对应相等的两个直角三角形全等
D、有两角和一边对应相等的两个直角三角形全等
3.如图1,在△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是
__________cm
4.如图2,已知:AD是△ABC中BC边上的高,E为AC上的一点,BE交AD于点F,且有BF=AC,FD=CD,求证:BE⊥AC
5.如图3,已知:AD=BC,BE⊥AC,DF⊥AC,且BE=DF。
求证:(1)△ABE≌△CDF;(2)AB∥CD
6.如图4,已知:∠A=90°,AB=BD,ED⊥BC于D。
求证:AE=ED
【提高练习】
1.如图所示的网格中(4×4的正方形),∠1+∠2+∠3+∠4+∠5+∠6=____________
2.已知:Rt△ABC中,∠ACB是直角,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,求证:CD⊥BE
3.已知△ABC中,CD⊥AB于D,过D作DE⊥AC,F为BC中点,过F作FG⊥DC,求证:DG=EG。
4.如图,A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=
CD,试证明BD平分EF
5.如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(4,4)处,两直角边与坐标轴交于点A和点B.
(1)求OA+OB的值;
(2)将直角三角形绕点P逆时针旋转,两直角边与坐标轴交于点A和点B,求OA+OB的值.
6. 已知:如图,在△ABC 中,D 是边BC 的中点,AD 是∠BAC 的角平分线,求证:△ABC 是
等腰三角形
7. 已知:如图,在两个同心圆中,O 是圆心,直线l 与大圆相交于A 、B 两点,与小圆相交于C 、D 两点,求证:AC =BD
8. 已知:如图,AD ⊥CD ,CD ∥AB ,CD =CE ,又AE ⊥BC ,垂足为E ,求证:AB =BC
9. 如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA 为a 米,此时,梯子的倾斜角为75°。
如果梯子底端不动,顶端靠在对面墙上N 处,此时梯子顶端距地面的垂直距离NB 为b 米,梯子的倾斜角45°,求这间房子的宽AB
10. CD 经过∠BCA 顶点C 的一条直线,CA=CB .E ,F 分别是直线CD 上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD 经过∠BCA 的内部,且E ,F 在射线CD 上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE_________CF ;EF_________|BE ﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA <180°,请添加一个关于∠α与∠BCA 关系的条件____________,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD 经过∠BCA 的外部,∠α=∠BCA ,请提出EF ,BE ,AF 三条线段数量关系的合理猜想.
【巩固练习】
1. 两个三角形的两条边及其中一条边的对角对应相等,则下列四个命题中,真命题的个数
是( )个
①这两个三角形全等; ②相等的角为锐角时全等 ③相等的角为钝角对全等; ④相等的角为直角时全等
A .0
B .1
C .2
D .3
2. 在下列定理中假命题是( )
A .一个等腰三角形必能分成两个全等的直角三角形
B .一个直角三角形必能分成两个等腰三角形
C .两个全等的直角三角形必能拼成一个等腰三角形
D .两个等腰三角形必能拼成一个直角三角形
3. 如图,Rt △ABC 中,∠B=90°,∠ACB=60°,延长BC 到D ,使CD=AC 则AC :BD=( )
A .1:1
B .3:1
C .4:1
D .2:3
4. 如图,在Rt △ABC 中,∠ACB=90°,CD 、CE ,分别是斜边AB 上的高与中线,CF 是∠ACB
的平分线。
则∠1与∠2的关系是( )
A .∠1<∠2
B .∠1=∠2;
C .∠1>∠2
D .不能确定
5. 如图,BE 和CF 是△ABC 的高,它们相交于点O ,且BE=CD ,则图中有_______对全等三
角形,其中能根据“HL ”来判定三角形全等的有_______对.
6. 如图,有两个长度相同的滑梯(即BC =EF ),左边滑梯的高度AC 与右边滑梯水平方向的
长度DF 相等,则∠ABC +∠DFE =___________度.
7. 已知:如图∠B=∠E=90°,AC=DF ,FB=EC ,求证:AB=DE.
8. 已知:如图AB ⊥BD ,CD ⊥BD ,AB=DC 求证:AD//BC.
【中考链接】
如图,△ABC 中,AD 是∠BAC 的角平分线,且BD=CD ,DE ,DF 分别垂直于AB ,AC ,垂足为E ,F .请你结合条件认真研究,然后写出三个正确的结论.
结论(1):
结论(2):
结论(3):
A B
C E
D O。
