C语言求素数问题算法
c语言求素数个数方法超时

c语言求素数个数方法超时(原创版2篇)目录(篇1)I.素数定义及性质II.常见的求素数个数方法III.C语言求素数个数方法IV.优化C语言求素数个数方法正文(篇1)I.素数定义及性质-----------素数又称质数,是指只能被1和自身整除的正整数。
例如,2、3、5、7等都是素数。
素数具有许多独特的性质,如素数无限性、素数间的关系、素数的应用等。
II.常见的求素数个数方法-------------1.试除法:通过不断试除每个整数,判断是否能被整除来判断该数是否为素数。
但效率较低,对于大数可能超时。
2.埃拉托色尼筛选法:通过筛选掉2、3、5等合数,缩小素数的搜索范围,但依然存在效率问题。
3.筛法:利用素数分布定理,先预处理出一部分素数,再用剩余的数除以已预处理的素数的余数来判断是否为素数。
但需要预处理,且对于大数仍存在超时问题。
III.C语言求素数个数方法-------------C语言求素数个数的方法主要有试除法和筛法两种。
试除法可以通过循环遍历每个整数,判断是否能被整除来判断该数是否为素数。
但效率较低,对于大数可能超时。
筛法可以利用预处理过的素数表来快速判断一个数是否为素数。
但需要预处理,且对于大数仍存在超时问题。
为了解决这些问题,我们可以使用摩尔投票筛法来优化C语言求素数个数的方法。
摩尔投票筛法的基本思想是利用试除法筛选掉大部分合数,再用剩余的合数除以已筛选的合数的余数来判断是否为素数。
具体实现步骤如下:1.初始化一个数组p,p[i]表示第i个合数的因子个数。
例如,p[2]=1,p[3]=2,p[5]=1,p[7]=2,p[11]=3,p[13]=2,p[17]=3,p[19]=2,p[31]=4等。
2.初始化一个数组t,t[i]表示第i个合数的因子个数是否大于等于p[i]。
例如,t[2]=0,t[3]=0,t[5]=0,t[7]=0,t[11]=0,t[13]=0,t[17]=0,t[19]=0,t[3 1]=0等。
C语言求素数问题算法

1.自然数是0,1,2……2.素数是2,3,5……(不包括1的只能背1和它本身整除的自然数)【1】求10000以内的所有素数。
素数是除了1和它本身之外再不能被其他数整除的自然数。
由于找不到一个通项公式来表示所有的素数,所以对于数学家来说,素数一直是一个未解之谜。
像著名的哥德巴赫猜想、孪生素数猜想,几百年来不知吸引了世界上多少优秀的数学家。
尽管他们苦心钻研,呕心沥血,但至今仍然未见分晓。
自从有了计算机之后,人们借助于计算机的威力,已经找到了2216091以内的所有素数。
求素数的方法有很多种,最简单的方法是根据素数的定义来求。
对于一个自然数N,用大于1小于N的各个自然数都去除一下N,如果都除不尽,则N为素数,否则N为合数。
但是,如果用素数定义的方法来编制计算机程序,它的效率一定是非常低的,其中有许多地方都值得改进。
第一,对于一个自然数N,只要能被一个非1非自身的数整除,它就肯定不是素数,所以不必再用其他的数去除。
第二,对于N来说,只需用小于N的素数去除就可以了。
例如,如果N能被15整除,实际上就能被3和5整除,如果N不能被3和5整除,那么N也决不会被15整除。
第三,对于N来说,不必用从2到N一1的所有素数去除,只需用小于等于√N(根号N)的所有素数去除就可以了。
这一点可以用反证法来证明:如果N是合数,则一定存在大于1小于N的整数d1和d2,使得N=d1×d2。
如果d1和d2均大于√N,则有:N=d1×d2>√N×√N=N。
而这是不可能的,所以,d1和d2中必有一个小于或等于√N。
基于上述分析,设计算法如下:(1)用2,3,5,7逐个试除N的方法求出100以内的所有素数。
(2)用100以内的所有素数逐个试除的方法求出10000以内的素数。
首先,将2,3,5,7分别存放在a[1]、a[2]、a[3]、a[4]中,以后每求出一个素数,只要不大于100,就依次存放在A 数组中的一个单元中。
C语言常用数值计算算法(素数、公约数、级数、方程根和定积分)
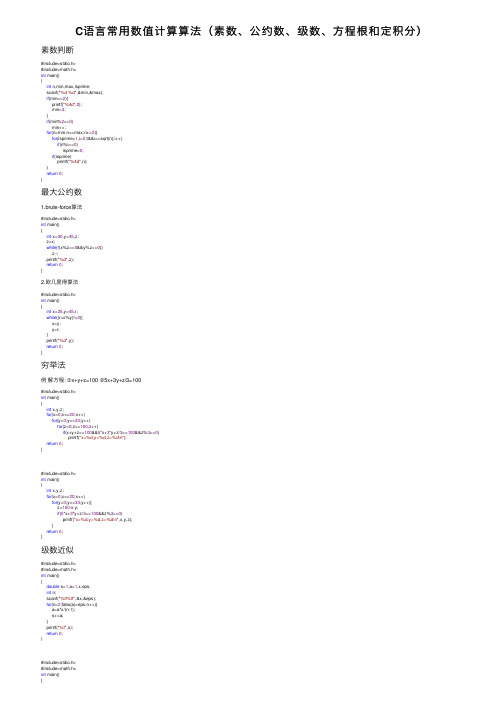
C语⾔常⽤数值计算算法(素数、公约数、级数、⽅程根和定积分)素数判断#include<stdio.h>#include<math.h>int main(){int n,min,max,isprime;scanf("%d %d",&min,&max);if(min<=2){printf("%4d",2);min=3;}if(min%2==0)min++;for(n=min;n<=max;n+=2){for(isprime=1,i=2;t&&i<=sqrt(n);i++)if(n%i==0)isprime=0;if(isprime)printf("%4d",n);}return0;}最⼤公约数1.brute-force算法#include<stdio.h>int main(){int x=30,y=45,z;z=x;while(!(x%z==0&&y%z==0))z--;printf("%d",z);return0;}2.欧⼏⾥得算法#include<stdio.h>int main(){int x=35,y=45,r;while((r=x%y)!=0){x=y;y=r;}printf("%d",y);return0;}穷举法例解⽅程: ①x+y+z=100 ②5x+3y+z/3=100#include<stdio.h>int main(){int x,y,z;for(x=0;x<=20;x++)for(y=0;y<=33;y++)for(z=0;z<=100;z++)if(x+y+z==100&&5*x+3*y+z/3==100&&z%3==0)printf("x=%d,y=%d,z=%d\n");return0;}#include<stdio.h>int main(){int x,y,z;for(x=0;x<=20;x++)for(y=0;y<=33;y++){z=100-x-y;if(5*x+3*y+z/3==100&&z%3==0)printf("x=%d,y=%d,z=%d\n",x,y,z);}return0;}级数近似#include<stdio.h>#include<math.h>int main(){double s=1,a=1,x,eps;int n;scanf("%lf%lf",&x,&eps);for(n=2;fabs(a)>eps;n++){a=a*x/(n-1);s+=a;}printf("%f",s);return0;)#include<stdio.h>#include<math.h>int main(){double sum,x,eps=1e-6,fn,tn;int s=1,n=2;scanf("%lf",&x);s=fn=x;do{s=-s;fn=fn*(2*n-3)/(2*n-2)*x*x;tn=sign*fn/(2*n-1);sum=sum+tn;n++;}while(fabs(tn)>eps);printf("%f",sum);⼀元⾮线性⽅程求根⼀、⽜顿迭代法 1.基本概念:如果函数连续,且待求零点孤⽴,那么在零点周围存在⼀个区域,当初值在这个邻域内时,⽜顿法收敛。
统计素数并求和c语言

统计素数并求和c语言素数的定义是,除了1和其自身可以被整除的数。
它们只能被1和自身整除,这种数叫做素数。
素数是自然数中的一种特殊的数,在数学中有许多素数的抽象理论。
在实际的编程应用中,统计素数及其求和是一个非常简单的操作,在c语言中,有两种方式可以实现这种功能:一种是通过“埃拉托斯特尼筛法”来求出一定范围内的素数,所谓“筛法”,是指将一定范围内的数字(从2开始)一个个“筛掉”,带被被筛当然都是素数,但是也可能会被2,3,5,7,11等素数筛掉。
然后再将剩下的数字全部相加,就可以得到该范围内的素数的和。
另一种是通过线性排序的方法来求解,将一定范围内的数字从小到大依次排列,然后将每一个数字除以它的前一个数字,如果出现余数。
则说明这个数字是一个素数,将所有的素数相加,就可以得到该范围内的素数的和。
总的来说,c语言中统计素数并求和有以上两种方法,下面将介绍利用埃拉托斯特尼筛法实现统计素数及求和的编程实例,以便读者能够更好地理解两种方法的应用。
编程实例:利用“埃拉托斯特尼筛法”统计素数并求和//求出从1~N的素数并求和#include <stdio.h>int main(void) {int N=1000; //要求求出从1~N的素数int prime[N+1],sum=0; //prime[N+1]用来标记是否为素数for(int i=0;i<N+1;i++) //初始化,全部初始化为1prime[i]=1;for(int i=2;i<=N;i++) { //从2开始筛选if(prime[i]==0) continue; //如果不是素数,则跳过for(int j=2*i;j<=N;j+=i) //将i倍数筛掉prime[j]=0;sum+=i;//求和}printf(从1~%d的素数和为:%dN,sum);return 0;}上面的程序中,首先用一个数组prime[N+1]来标记是否为素数,全部初始化为1,然后从2开始进行筛选,找出所有的素数,并将素数求和。
素数对猜想c语言

素数对猜想c语言素数对猜想是一个数学问题,它要求找到两个素数,它们的差是唯一的偶数。
在 C 语言中,可以通过编写程序来搜索符合条件的素数对。
以下是一个简单的实现方法:1. 先定义一个数组,其中存储着所有小于给定规模的素数。
2. 然后定义一个变量表示当前已知的最小素数,它每次被找到时都会被更新。
3. 在循环中,每次迭代都会检查当前已知的最小素数是否等于当前数值,如果是,那么它就被更新为当前数值减去 2。
4. 如果当前数值是偶数,那么就需要检查是否存在已知的素数对,如果存在,那么就需要更新这些素数对中任意一对的数值。
5. 重复执行循环,直到找到符合条件的素数对或者确定不存在符合条件的素数对。
以下是一个示例代码,它使用上述方法搜索符合条件的素数对: ```c#include <stdio.h>#include <stdbool.h>// 存储所有小于给定规模的素数的数组int prime_array[100001];// 初始化所有素数void initialize_prime_array() {for (int i = 2; i <= sqrt(prime_array[0]); i++) {if (prime_array[i] == 0) {prime_array[i] = 1;}}}// 查找符合条件的素数对bool find_prime_pair(int min_prime, int max_prime) { bool found_pair = false;// 更新最小素数int current_prime = min_prime;while (current_prime != max_prime) {if (prime_array[current_prime] == 0) {current_prime = prime_array[current_prime] + 2;found_pair = true;break;}current_prime++;}return found_pair;}int main() {initialize_prime_array();bool found_pair = find_prime_pair(2, 100000);if (found_pair) {printf("The prime pair is %d and %d", found_pair ? 2 : 1, found_pair + 2);} else {printf("No prime pair is found");}return 0;}```该程序使用 `prime_array` 数组来存储所有小于给定规模的素数,`initialize_prime_array` 函数用于初始化所有素数,`find_prime_pair` 函数用于查找符合条件的素数对,`main` 函数是程序的主函数。
最大素数c语言

最大素数的求解1. 什么是素数?素数是指只能被1和自身整除的正整数。
在数学中,素数也被称为质数。
素数是数字领域中的基本概念,对于很多数论问题都起到了至关重要的作用。
2. 如何判断一个数是否为素数?判断一个数是否为素数有多种方法,下面介绍两种常用的判断素数的方法。
2.1 蛮力法蛮力法是一种最简单直接的判断素数的方法,其基本思想是对待判断的数从2开始,逐个除以所有小于它的自然数,如果能被除尽,则该数不是素数;如果不能被除尽,则该数是素数。
蛮力法的C语言代码如下:#include <stdio.h>int isPrime(int num) {if (num < 2) {return 0;}for (int i = 2; i * i <= num; i++) {if (num % i == 0) {return 0;}}return 1;}int main() {int n;printf("请输入一个正整数: ");scanf("%d", &n);if (isPrime(n)) {printf("%d是素数\n", n);} else {printf("%d不是素数\n", n);}return 0;}2.2 埃氏筛法埃氏筛法是一种更高效的判断素数的方法,其基本思想是从2开始,将每个素数的倍数标记为合数,直到遍历完所有小于等于待判断数的自然数,剩下的未被标记的数即为素数。
埃氏筛法的C语言代码如下:#include <stdio.h>#include <stdbool.h>void sieveOfEratosthenes(int n) {bool isPrime[n+1];for (int i = 2; i <= n; i++) {isPrime[i] = true;}for (int i = 2; i * i <= n; i++) {if (isPrime[i]) {for (int j = i * i; j <= n; j += i) {isPrime[j] = false;}}}printf("小于等于%d的素数有: ", n);for (int i = 2; i <= n; i++) {if (isPrime[i]) {printf("%d ", i);}}printf("\n");}int main() {int n;printf("请输入一个正整数: ");scanf("%d", &n);sieveOfEratosthenes(n);return 0;}3. 求解最大素数有了判断素数的方法,我们可以通过遍历一定范围内的数,找到其中的最大素数。
素数c语言程序编写

素数c语言程序编写素数是指只能被1和自身整除的正整数,如2、3、5、7等。
在计算机编程中,判断一个数是否为素数是一个常见的问题。
下面我们来介绍一下如何用C语言编写素数程序。
首先,我们需要明确一个概念:质数。
质数是指除了1和本身之外,不能被其他正整数整除的正整数。
因此,素数和质数是同义词。
接下来,我们来看一下如何用C语言编写素数程序。
下面是一个简单的示例代码:```#include <stdio.h>int main(){int n, i, flag = 0;printf("Enter a positive integer: ");scanf("%d", &n);for(i=2; i<=n/2; ++i){if(n%i == 0){flag = 1;break;}}if (n == 1){printf("1 is not a prime number.\n");}else{if (flag == 0)printf("%d is a prime number.\n", n);elseprintf("%d is not a prime number.\n", n); }return 0;}```这个程序的作用是判断输入的正整数是否为素数。
程序首先要求用户输入一个正整数,然后通过for循环从2开始到n/2进行遍历,判断n是否能被i整除。
如果能被整除,则说明n不是素数,将flag标记为1,跳出循环。
最后根据flag的值输出结果。
需要注意的是,1不是素数,因此需要特殊处理。
如果输入的是1,则直接输出“1 is not a prime number.”。
此外,还有一些优化的方法可以提高程序的效率。
比如,可以只遍历到sqrt(n)即可,因为如果n能被大于sqrt(n)的数整除,那么一定能被小于sqrt(n)的数整除。
C语言求质数

【C语言】求解素数(质数)的N种境界★试除法:首先要介绍的,当然非"试除法"莫属。
"试除",顾名思义,就是不断地尝试能否整除。
比如要判断自然数x 是否质数,就不断尝试小于x 且大于1的自然数,只要有一个能整除,则x 是合数;否则,x 是素数。
显然,试除法是最容易想到的思路。
不客气地说,也是最平庸的思路。
不过呢,这个最平庸的思路,也有好多种境界。
不信请看下文:◎境界1假设要判断x 是否为质数,就从2 一直尝试到x-1。
这种做法,其效率应该是最差的1.#include<stdio.h>2.#include<Windows.h>3.int main()4.{5. int i = 0,k = 0;6. int count = 0;7. for(i=100; i<=200; i++)8. {9. for(k=2; k<i; k++)10. {11. if(i%k == 0)12. break;13. }14. if(k == i)15. printf("%d是素数\n",i);16. count++;17. }18. printf("\n%4d",count);19. system("pause");20. return 0;}◎境界2所有素数都是偶数,因此可以加快步长1.#include<stdio.h>2.#include<Windows.h>3.int main()4.{5. int i = 0, k = 0;6. int count = 0;7. for(i=101; i<=200; i+=2)8. {9. for(k=2; k<i; k++)10. {11. if(i%k == 0)12. break;13. }14. if(k==i)15. printf("%d是素数\n",i);16. count++;17. }18. printf("\n%4d",count);19. system("pause");20. return 0;21.}◎境界3除了2以外,所有可能的质因数都是奇数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.自然数是0,1,2……2.素数是2,3,5……(不包括1的只能背1和它本身整除的自然数)【1】求10000以内的所有素数。
素数是除了1和它本身之外再不能被其他数整除的自然数。
由于找不到一个通项公式来表示所有的素数,所以对于数学家来说,素数一直是一个未解之谜。
像著名的哥德巴赫猜想、孪生素数猜想,几百年来不知吸引了世界上多少优秀的数学家。
尽管他们苦心钻研,呕心沥血,但至今仍然未见分晓。
自从有了计算机之后,人们借助于计算机的威力,已经找到了2216091以内的所有素数。
求素数的方法有很多种,最简单的方法是根据素数的定义来求。
对于一个自然数N,用大于1小于N的各个自然数都去除一下N,如果都除不尽,则N为素数,否则N为合数。
但是,如果用素数定义的方法来编制计算机程序,它的效率一定是非常低的,其中有许多地方都值得改进。
第一,对于一个自然数N,只要能被一个非1非自身的数整除,它就肯定不是素数,所以不必再用其他的数去除。
第二,对于N来说,只需用小于N的素数去除就可以了。
例如,如果N能被15整除,实际上就能被3和5整除,如果N不能被3和5整除,那么N也决不会被15整除。
第三,对于N来说,不必用从2到N一1的所有素数去除,只需用小于等于√N(根号N)的所有素数去除就可以了。
这一点可以用反证法来证明:如果N是合数,则一定存在大于1小于N的整数d1和d2,使得N=d1×d2。
如果d1和d2均大于√N,则有:N=d1×d2>√N×√N=N。
而这是不可能的,所以,d1和d2中必有一个小于或等于√N。
基于上述分析,设计算法如下:(1)用2,3,5,7逐个试除N的方法求出100以内的所有素数。
(2)用100以内的所有素数逐个试除的方法求出10000以内的素数。
首先,将2,3,5,7分别存放在a[1]、a[2]、a[3]、a[4]中,以后每求出一个素数,只要不大于100,就依次存放在A 数组中的一个单元中。
当我们求100—10000之间的素数时,可依次用a[1]-a[2]的素数去试除N,这个范围内的素数可以不保存,直接打印。
【2】用筛法求素数。
简单介绍一下厄拉多塞筛法。
厄拉多塞是一位古希腊数学家,他在寻找素数时,采用了一种与众不同的方法:先将2-N的在2的上面画一个圆圈,然后划去2的其他倍数;第一个既未画圈又没有被划去的数是3,将它画圈,再划去3的其他倍数;现在既未画圈又没有被划去的第一个数是5,将它画圈,并划去5的其他倍数……依次类推,一直到所有小于或等于N 的各数都画了圈或划去为止。
这时,表中画了圈的以及未划去的那些数正好就是小于N的素数。
这很像一面筛子,把满足条件的数留下来,把不满足条件的数筛掉。
由于这种方法是厄拉多塞首先发明的,所以,后人就把这种方法称作厄拉多塞筛法。
在计算机中,筛法可以用给数组单元置零的方法来实现。
具体来说就是:首先开一个数组:a[i],i=1,2,3,…,同时,令所有的数组元素都等于下标值,即a[i]=i,当i不是素数时,令a[i]=0 。
当输出结果时,只要判断a[i]是否等于零即可,如果a[i]=0,则令i=i+1,检查下一个a[i]。
筛法是计算机程序设计中常用的算法之一。
【3】用6N±1法求素数。
任何一个自然数,总可以表示成为如下的形式之一:6N,6N+1,6N+2,6N+3,6N+4,6N+5 (N=0,1,2,…)显然,当N≥1时,6N,6N+2,6N+3,6N+4都不是素数,只有形如6N+1和6N+5的自然数有可能是素数。
所以,除了2和3之外,所有的素数都可以表示成6N±1的形式(N为自然数)。
根据上述分析,我们可以构造另一面筛子,只对形如6 N±1的自然数进行筛选,这样就可以大大减少筛选的次数,从而进一步提高程序的运行效率和速度。
在程序上,我们可以用一个二重循环实现这一点,外循环i按3的倍数递增,内循环j为0-1的循环,则2(i+j)-1恰好就是形如6N±1的自然数。
代码:时间复杂度O(n).代码:时间复杂度O(n/2), 速度提高一倍.定理: 如果n不是素数, 则n有满足1<d<=sqrt(n)的一个因子d.证明: 如果n不是素数, 则由定义n有一个因子d满足1<d<n.如果d大于sqrt(n), 则n/d是满足1<n/d<=sqrt(n)的一个因子.代码: 时间复杂度O(sqrt(n)/2), 速度提高O((n-sqrt(n))/2).例如: 11%3 != 0 可以确定11%(3*i) != 0.定理: 如果n不是素数, 则n有满足1<d<=sqrt(n)的一个"素数"因子d.证明:I1. 如果n不是素数, 则n有满足1< d <=sqrt(n)I2. 如果d是素数, 则定理得证, 算法终止.I3. 令n=d, 并转到步骤I1.由于不可能无限分解n的因子, 因此上述证明的算法最终会停止.代码:假设n范围内的素数个数为PI(n), 则时间复杂度O(PI(sqrt(n))).函数PI(x)满足素数定理: ln(x)-3/2 < x/PI(x) < ln(x)-1/2, 当x >= 67时.因此O(PI(sqrt(n)))可以表示为O(sqrt(x)/(ln(sqrt(x))-3/2)),O(sqrt(x)/(ln(sqrt(x))-3/2))也是这个算法的空间复杂度.5. 构造素数序列primes[i]: 2, 3, 5, 7, ...由4的算法我们知道, 在素数序列已经被构造的情况下, 判断n是否为素数效率很高; 但是, 在构造素数序列本身的时候, 是否也可是达到最好的效率呢?事实上这是可以的! -- 我们在构造的时候完全可以利用已经被构造的素数序列!假设我们已经我素数序列: p1, p2, .. pn现在要判断pn+1是否是素数, 则需要(1, sqrt(pn+1)]范围内的所有素数序列,而这个素数序列显然已经作为p1, p2, .. pn的一个子集被包含了!代码:在一定的应用范围内, 我们可以把近似认为makePrimes需要常数时间.在后面的讨论中, 我们将探讨一种对计算机而言更好的makePrimes方法.6. 更好地利用计算机资源...当前的主流PC中, 一个整数的大小为2^32. 如果需要判断2^32大小的数是否为素数,则可能需要测试[2, 2^16]范围内的所有素数(2^16 == sqrt(2^32)).由4中提到的素数定理我们可以大概确定[2, 2^16]范围内的素数个数.由于2^16/(ln(2^16)-1/2) = 6138, 2^16/(ln(2^16)-3/2) = 6834,我们可以大概估计出[2, 2^16]范围内的素数个数6138 < PI(2^16) < 6834.在对[2, 2^16]范围内的素数进行统计, 发现只有6542个素数:p_6542: 65521, 65521^2 = 4293001441 < 2^32, (2^32 = 4294967296)p_6543: 65537, 65537^2 = 4295098369 > 2^32, (2^32 = 4294967296)在实际运算时unsigned long x = 4295098369;将发生溢出, 为131073.在程序中, 我是采用double类型计算得到的结果.分析到这里我们可以看到, 我们只需要缓冲6543个素数, 我们就可以采用4中的算法高效率地判断[2, 2^32]如此庞大范围内的素数!(原本的2^32大小的问题规模现在已经被减小到6543规模了!)虽然用现在的计算机处理[2, 2^16]范围内的6542个素数已经没有一点问题,虽然makePrimes只要被运行一次就可以, 但是我们还是考虑一下是否被改进的可能?!我想学过java的人肯定想把makePrimes作为一个静态的初始化实现, 在C++中也可以模拟java中静态的初始化的类似实现:#define NELEMS(x) ((sizeof(x)) / (sizeof((x)[0])))static int primes[6542+1];static struct _Init { _Init(){makePrimes(primes, NELEMS(primes);} } _init;如此, 就可以在程序启动的时候自动掉用makePrimes初始化素数序列.但, 我现在的想法是: 为什么我们不能在编译的时候调用makePrimes函数呢?完全可以!!! 代码如下:有点不可思议吧, 原本makePrimes需要花费的时间复杂度现在真的变成O(1)了!(我觉得叫O(0)可能更合适!) 7. 二分法查找现在我们缓存了前大约sqrt(2^32)/(ln(sqrt(2^32)-3/2))个素数列表, 在判断2^32级别的素数时最多也只需要PI(sqrt(2^32))次判断(准确值是6543次), 但是否还有其他的方式判断呢?当素数比较小的时候(不大于2^16), 是否可以直接从缓存的素数列表中直接查询得到呢?答案是肯定的! 由于primes是一个有序的数列, 因此我们当素数小于2^16时, 我们可以直接采用二分法从primes中查询得到(如果查询失败则不是素数).代码:时间复杂度:if(n <= primes[NELEMS(primes)-1] && n >= 67): O(log2(NELEMS(primes))) < 13;if(n > primes[NELEMS(primes)-1]): O(PI(sqrt(n))) <= NELEMS(primes).8. 素数定理+2分法查找在7中, 我们对小等于primes[NELEMS(primes)-1]的数采用2分法查找进行判断.我们之前针对2^32缓冲的6453个素数需要判断的次数为13次(log2(1024*8) == 13).对于小的素数而言(其实就是2^16范围只内的数), 13次的比较已经完全可以接受了.不过根据素数定理: ln(x)-3/2 < x/PI(x) < ln(x)-1/2, 当x >= 67时, 我们依然可以进一步缩小小于2^32情况的查找范围(现在是0到NELEMS(primes)-1范围查找).我们需要解决问题是(n <= primes[NELEMS(primes)-1):如果n为素数, 那么它在素数序列可能出现的范围在哪?---- (n/(ln(n)-1/2), n/(ln(n)-3/2)), 即素数定理!上面的代码修改如下:时间复杂度:if(n <= primes[NELEMS(primes)-1] && n >= 67): O(log2(hi-lo))) < ???;if(n > primes[NELEMS(primes)-1]): O(PI(sqrt(n))) <= NELEMS(primes).9. 打包成素数库(给出全部的代码)到目前为止, 我已经给出了我所知道所有改进的方法(如果有人有更好的算法感谢告诉我).这里需要强调的一点是, 这里讨论的素数求法是针对0-2^32范围的数而言, 至于像寻找成百上千位大小的数不在此讨论范围, 那应该算是纯数学的内容了.代码保存在2个文件: prime.h, prime.cpp.代码:到这里, 关于素数的讨论基本告一段落. 回顾我们之前的求解过程, 我们会发现如果缺少数学的基本知识会很难设计好的算法; 但是如果一味地只考虑数学原理,而忽律了计算机的本质特征, 也会有同样的问题.一个很常见的例子就是求Fibonacci数列. 当然方法很多, 但是在目前的计算机中都没有实现的必要!因为Fibonacci数列本身是指数增长的, 32位的有符号整数所能表示的位置只有前46个:因此, 我只需要把前46个Fibonacci数保存到数组中就可以搞定了!比如: F(int i) = {return Fibonacci[i];} 非常简单, 效率也非常好.。
