大学概率论之条件概率乘法公式
合集下载
条件概率乘法公式

P ( AB) P ( B) 0.4 P ( B | A) 0.5 P ( A) P ( A) 0.8
条件概率P(A|B)与P(A)的区别
每一个随机试验都是在一定条件下进行 的,设A是随机试验的一个事件,则P(A)是在 该试验条件下事件A发生的可能性大小.
而条件概率P(A|B)是在原条件下又添加 “B发生”这个条件时A发生的可能性大小, 即P(A|B)仍是概率.
设B={零件是乙厂生产}
300个 300个
乙厂生产
A={是标准件} 所求为P(AB).
乙厂生产
189个是
标准件
甲、乙共生产
1000 个
设B={零件是乙厂生产} 300个
A={是标准件} 所求为P(AB) .
乙厂生产
189个是
标准件
甲、乙共生产
若改为“发现它是乙厂生产的, 问它是标准件的概率是多少?”
监狱看守通知三个囚犯, 在他们中要随机 地选出一个处决 , 而把另外两个释放. 囚犯 甲请求看守秘密地告诉他,另外两个囚犯中谁 将获得自由.
丙 乙 甲
因为我已经知道他们两人中 至少有一人要获得自由,所 以你泄露这点消息是无妨的.
NO!
如果你知道了你的同伙中谁将获释, 那么,你自己被处决的概率就由 1/3增加到1/2,因为你就成了剩下的 两个囚犯中的一个了.
(5) 可列可加性 :设 B1 , B2 , 是两两不相容的事 件,则有
P Bi A P ( Bi A). i 1 i 1
4. 条件概率的计算 1) 用定义计算: P ( AB) P ( A | B) , P(B)>0 P ( B) 掷骰子 2)从加入条件后改变了的情况去算
P(A)与P(A |B)的区别在于两者发生的条件不同, 它们是两个不同的概念,在数值上一般也不同.
条件概率P(A|B)与P(A)的区别
每一个随机试验都是在一定条件下进行 的,设A是随机试验的一个事件,则P(A)是在 该试验条件下事件A发生的可能性大小.
而条件概率P(A|B)是在原条件下又添加 “B发生”这个条件时A发生的可能性大小, 即P(A|B)仍是概率.
设B={零件是乙厂生产}
300个 300个
乙厂生产
A={是标准件} 所求为P(AB).
乙厂生产
189个是
标准件
甲、乙共生产
1000 个
设B={零件是乙厂生产} 300个
A={是标准件} 所求为P(AB) .
乙厂生产
189个是
标准件
甲、乙共生产
若改为“发现它是乙厂生产的, 问它是标准件的概率是多少?”
监狱看守通知三个囚犯, 在他们中要随机 地选出一个处决 , 而把另外两个释放. 囚犯 甲请求看守秘密地告诉他,另外两个囚犯中谁 将获得自由.
丙 乙 甲
因为我已经知道他们两人中 至少有一人要获得自由,所 以你泄露这点消息是无妨的.
NO!
如果你知道了你的同伙中谁将获释, 那么,你自己被处决的概率就由 1/3增加到1/2,因为你就成了剩下的 两个囚犯中的一个了.
(5) 可列可加性 :设 B1 , B2 , 是两两不相容的事 件,则有
P Bi A P ( Bi A). i 1 i 1
4. 条件概率的计算 1) 用定义计算: P ( AB) P ( A | B) , P(B)>0 P ( B) 掷骰子 2)从加入条件后改变了的情况去算
P(A)与P(A |B)的区别在于两者发生的条件不同, 它们是两个不同的概念,在数值上一般也不同.
条件概率和乘法公式

机器学习算法
朴素贝叶斯分类器
01
朴素贝叶斯分类器是一种基于贝叶斯定理的分类算法,它利用
条件概率和乘法公式来计算给定特征下类别的概率。
隐马尔可夫模型
02
隐马尔可夫模型是一种用于序列标注和预测的模型,它利用条
件概率和乘法公式来计算状态转移和观测的概率。
条件随机场
03
条件随机场是一种用于自然语言处理的模型,它利用条件概率
03
在学习和应用概率论的过程中,我们需要注重培养自己的逻辑思维和分析能力 。通过深入思考和探究概率论中的问题,我们可以提高自己的数学素养和解决 问题的能力,为未来的学习和工作打下坚实的基础。
THANKS
感谢观看
• 在学习条件概率和乘法公式的过程中,我们需要掌握相关的概念和公式,并能 够灵活运用它们解决实际问题。同时,我们还需要了解条件概率和乘法公式的 局限性和假设条件,以避免在实际应用中出现错误。
• 除了条件概率和乘法公式,概率论中还有许多其他重要的概念和公式,例如全 概率公式、贝叶斯公式、独立性等。这些概念和公式之间有着密切的联系和相 互影响,我们需要系统地学习和理解它们,以建立完整的概率论知识体系。
02
乘法公式及其应用
乘法公式的推导
01
定义
乘法公式描述了两个事件A和B同时发生的概率与事件A发生的概率和事
件B发生的概率之间的关系。
02 03
推导
乘法公式基于概率的独立性假设,即事件A的发生不影响事件B的发生, 反之亦然。因此,事件A和事件B同时发生的概率等于各自发生的概率 的乘积。
公式
$P(A cap B) = P(A) times P(B)$
展望Βιβλιοθήκη 01随着科技的不断发展,概率论在各个领域的应用越来越广泛。未来,条件概率 和乘法公式等概率论知识将更加受到重视和应用。
14条件概率和乘法公式
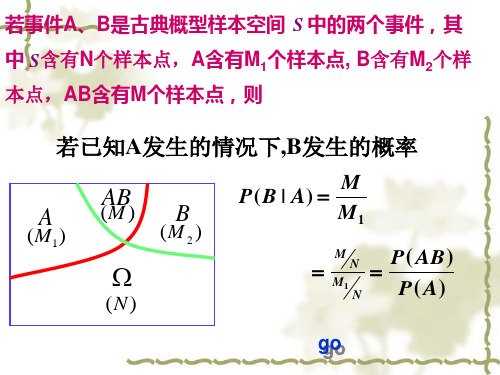
球的取法为 P31P41, 其中, 第二次取得白球的取法
有 P31P21 种, 所以
P(B | A)
P31 P21 P31 P41
1 2
.
例 2 袋中有 5 个球, 其中 3 个红球 2 个白球, 现
从袋中不放回地连取两个, 已知第一次取得红球 时, 求第二次取得白球的概率.
解法 1 也可以直接用公式 (1) 计算, 因为第一次取走了一 个红球, 袋中只剩下 4 个球, 其中有两个白球, 再 从中任取一个, 取得白球的概率为 2/4, 所以
解 设 A {能活20年以上}, B {能活25年以上}
所求为P(B | A). 依题意,有
P( A)
P( AB) P( A)
P(B) P( A)
0.4 0.8
0.5.
三. 乘法公式 乘法公式:
P( AB) P( A)P(B A) (P( A) 0) P(B)P( A B) (P(B) 0)
解 记 Ai 为事件“第i 次取到的是黑球”(i 1,2). (1) 在已知 A1 发生, 即第一次取到的是黑球的条件 下, 第二次取球就在剩下的 2 个黑球、7 个白球共 9 个球中任取一个, 根据古典概率计算, 即有
P( A2 | A1) 2 / 9.
解 (2) 在已知 A2 发生, 即第二次取到的是黑球的
一. 条件概率的定义 设A,B为同一个随机试验中的两个随机事件 ,
且P(A)>0, 则
P(B | A) P( AB) P( A)
为在事件A发生的条件下,事件B发生的条件概率. 相应地,p(B)称为无条件概率.
条件概率 P(A|B)的样本空间
BA
BA
Sample space
P( AB)
概率论与数理统计公式总结(湖南大学)

(3) = ~t(n-1)
2.设 的 和 两个样本,则有:
(1)
5.相关性
对于随机变量X,Y下列结论是等价的:
(1)X与Y不相关 (3)ρ=0 (5)D(X Y)=D(X)+D(Y)
(2)Cov(X,Y)=0 (4)E(XY)=E(X)E(Y)
X,Y相互独立可以推出上述五个结论。
※切比雪夫不等式
表明:对于任意正数ε,当随机变量X的方差越小时,事件 的概率越小,其对立面概率越大。
则
定理(2)X Y相互独立,g(x)和h(y)是两个一元连续函数,则g(X)和h(Y)也相互独立。
定理(3) 则 。且 只差一个常数因子。
(重点)※期望与方差的性质
1期望的性质
(1)一维的:
若Y=g(X),
二维的:
若Z=g(X,Y),
(2)性质:E(C)=C E(CX)=CE(X) (C为常数)
E(X+Y)=E(X)+E(Y)
3.边缘概率密度函数
4.二维正态分布(还是看一下会比较好)
(1)二维正态分布中X,Y相互独立的充要条件是参数ρ(相关系数)=0
※连续型随机变量之和的分布
1.一般地:
卷积公式:
2.其他分布
(1)瑞利分布: X, Y均服从N(0, )则 的概率密度为
(2)Max与Min 分布:(自己推广到n个变量的情况)
(3)若X,Y独立,则Cov(X,Y)=0
(4)Cov(aX,bY)=abCov(X,Y)
(5)Cov( )=Cov( Y)+Cov( )
3.标准化随机变量
4.相关系数
也可写做为X,Y的标准化协随机变量的协方差
性质:(1)
(2)|ρ|=1的充要条件,存在常数a,b(b不等于0),使P{Y=a+bX}=1即X,Y以概率1线性相关。
2.设 的 和 两个样本,则有:
(1)
5.相关性
对于随机变量X,Y下列结论是等价的:
(1)X与Y不相关 (3)ρ=0 (5)D(X Y)=D(X)+D(Y)
(2)Cov(X,Y)=0 (4)E(XY)=E(X)E(Y)
X,Y相互独立可以推出上述五个结论。
※切比雪夫不等式
表明:对于任意正数ε,当随机变量X的方差越小时,事件 的概率越小,其对立面概率越大。
则
定理(2)X Y相互独立,g(x)和h(y)是两个一元连续函数,则g(X)和h(Y)也相互独立。
定理(3) 则 。且 只差一个常数因子。
(重点)※期望与方差的性质
1期望的性质
(1)一维的:
若Y=g(X),
二维的:
若Z=g(X,Y),
(2)性质:E(C)=C E(CX)=CE(X) (C为常数)
E(X+Y)=E(X)+E(Y)
3.边缘概率密度函数
4.二维正态分布(还是看一下会比较好)
(1)二维正态分布中X,Y相互独立的充要条件是参数ρ(相关系数)=0
※连续型随机变量之和的分布
1.一般地:
卷积公式:
2.其他分布
(1)瑞利分布: X, Y均服从N(0, )则 的概率密度为
(2)Max与Min 分布:(自己推广到n个变量的情况)
(3)若X,Y独立,则Cov(X,Y)=0
(4)Cov(aX,bY)=abCov(X,Y)
(5)Cov( )=Cov( Y)+Cov( )
3.标准化随机变量
4.相关系数
也可写做为X,Y的标准化协随机变量的协方差
性质:(1)
(2)|ρ|=1的充要条件,存在常数a,b(b不等于0),使P{Y=a+bX}=1即X,Y以概率1线性相关。
概率论乘法公式

设B={零件是乙厂生产}
300个
A={是标准件} 乙厂生产 所求为P(AB).
300个
乙厂生产
189个是
标准件
甲、乙共生产
1000 个
4
设B={零件是乙厂生产} 300个
A={是标准件}
乙厂生产
所求为P(AB) .
若改为“发现它是乙厂生产的, 问它是标准件的概率是多少?”
189个是
标准件
甲、乙共生产
优名酒各一瓶,第 三个拿到两瓶国 优名酒
从而: P (A) B 0 .4C 6 0 .57 3 0 .06 6 0 .0 71
20
例 设某光学仪器厂制造的透镜,第一次落下时 1
打二破 次的 落概 下率破为的概2 率,为若第107 一, 若次前落两下次时落未下打未破打,第 破, 第三次打破的概率为 9
b b c r r c brbrcbr 2 cbr 3 c
当 c>0 时,由于每次取出球后会增加下 一次也取到同色球的概率. 这是一个传染病 模型. 每次发现一个传染病患者,都会增加 再传染的概率.
14
一场精彩的足球赛将要举行,
5个球迷好不容易才搞到一张入场券. 大家都想去,只好用抽签的方法来解决.
第1个人抽到入场券的概率是1/5.
16
由于 A2 A1A2
由乘法公式
因为若第2个人抽到
了入场券,第1个人
P (A 2)P (A 1 )P (A 2|A 1 ) 肯定没抽到.
也就是要想第2个人抽到入场券,必须第1 个人未抽到,
计算得: P(A2)= (4/5)(1/4)= 1/5
17
同理,第3个人要抽到“入场券”,必须 第1、第2个人都没有抽到. 因此
条件概率和概率的乘法公式

一、全概率公式
例
一个盒子中有6只白球、4只黑球,从中不放回 地每次任取1只,连取2次,求第二次取到白球 的概率 A={第一次取到白球} ,且AB与 A B
解
因为 B=AB∪ A B
互不相容,所以
P ( B ) P ( A B ) P ( A B )
P ( A ) P ( B A ) P ( A ) P ( B A )
P ( A B ) P ( B ) ( B A ) 0 . 8 所求概率为 P P ( A ) P ( A )
甲,乙,丙3人参加面试抽签,每人的试题通过
不放回抽签的方式确定。假设被抽的10个试题签中有4
个是难题签,按甲先,乙次,丙最后的次序抽签。试求
1)甲抽到难题签,2)甲和乙都抽到难题签,3)甲没
B 1 =“第一个是男孩”
于是得
B
1
={(男, 男) , (男 , 女) }
3 1 P B BA P A P 4 4 1 1 P B1 P B P A 1A 2 4
乘法法则
P(AB) P(A)P(B A) P(B)P(A B)
P( AB) P(B A) P( A) P( AB) P( A B) P(B)
解
设从这批种子中任选一颗是一等,二等,三等,四 等种子的事件分别是A1,A2,A3,A4,则它们构 成完备事件组,又设B表示任选一颗种子所结的穗含 有50粒以上麦粒这一事件,则由全概率公式:
4 i 1
P ( B ) P ( A P ( BA i) i)
=95.5%×0.5+2%×0.15+1.5%×0.1+1%×0.05 =0.4825
贝叶斯公式 Bayes’ Theorem
概率论公式

n
注:如果有 n 个变量服从同一个 0-1 分布, Xi ~ b(1, p) ,则其和 X Xi 服从二项 i
分布 X ~ b(n, p)
11. Poisson 分布
X ~ P() P( X k) k e , k 0,1,...
F
(x)
0, 1,
x x
c c
E(X ) c
Var( X ) 0
9. 二项分布
X ~ b(n, p)
P( X k) Cnk pk (1 p)nk E(X ) np
Var( X ) np(1 p)
10. 二点分布(0-1 分布)
X ~ b(1, p)
P( X x) px (1 p)1x , x 0,1
p(
x)
2
n 2
1 (
n
)
e
x 2
x
n 2
1
,
x
0
2
0, x 0
E(X ) n
Var( X ) 2n
Gamma 分布变为 2 分布:
当 X ~ Ga(,) ,则 2 X ~ Ga(, 1) 2 (2 ) 2
20. 严格单调函数Y g(X )
pY ( y) px[h(x)] | h '(x) |
21. K 阶原点矩和中心矩
k E(X k ) k E( X E( X ))k
中心矩和原点矩关系:
k
k Cik i (i )ki i0
22. 变异系数
Cv
(
X
)
( E(
第一章 第三讲 条件概率、乘法公式、全概率公式

解: 样本空间 S ={(1,1),(1,2),„,(1,6), (2,1 )„,(2,6), „,(6,6)}, B ={(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)}, A ={(1,3),(2,2),(3,1)}, A B ={(2,2)}. 于是 P(A|B)= P(AB)/ P(B)=(1/36)/(6/36)=1/6 .
使用全概率公式关键在于寻找另一组形式:
P ( A ) P ( A B ) P ( B ) P ( A B ) P ( B ).
第一章 第三讲 条件概率、乘法公式、全概率公式
例4
设10 件产品中有 3 件不合格品,从中不放
回地取两次,每次一件,求取出的第二件为
注:若 B 已发生,为使 A 也发生,
则此样本点必属于A B ,
B S AB A
B成为了新的样本空间.
第一章 第三讲 条件概率、乘法公式、全概率公式
容易验证,条件概率满足以下性质: 1、对于事件A,有 0≤P(A|B)≤1;
2、对于必然事件S,有P(S |B) =1;
3、若事件A1,A2 ,„,An ,两两互不相容,则有 P(A1∪A2 ∪ „ ∪ An |B)= P(A1|B)+ P(A2|B )+ „ + P (An |B).
问题的提出: 1) 10个人摸彩,有3张中彩. 问:第1个人中彩的概率为多少? 第2个人中彩的概率为多少? 2) 10个人摸彩,有3张中彩. 问:已知第1个人没摸中, 第2个人中彩的概率为多少?
第一章 第三讲 条件概率、乘法公式、全概率公式
• 引例 10个产品中有7个正品、3个次品, 从中不放回地抽取两个, 已知第一个取到 次品,求第二个又取到次品的概率.
使用全概率公式关键在于寻找另一组形式:
P ( A ) P ( A B ) P ( B ) P ( A B ) P ( B ).
第一章 第三讲 条件概率、乘法公式、全概率公式
例4
设10 件产品中有 3 件不合格品,从中不放
回地取两次,每次一件,求取出的第二件为
注:若 B 已发生,为使 A 也发生,
则此样本点必属于A B ,
B S AB A
B成为了新的样本空间.
第一章 第三讲 条件概率、乘法公式、全概率公式
容易验证,条件概率满足以下性质: 1、对于事件A,有 0≤P(A|B)≤1;
2、对于必然事件S,有P(S |B) =1;
3、若事件A1,A2 ,„,An ,两两互不相容,则有 P(A1∪A2 ∪ „ ∪ An |B)= P(A1|B)+ P(A2|B )+ „ + P (An |B).
问题的提出: 1) 10个人摸彩,有3张中彩. 问:第1个人中彩的概率为多少? 第2个人中彩的概率为多少? 2) 10个人摸彩,有3张中彩. 问:已知第1个人没摸中, 第2个人中彩的概率为多少?
第一章 第三讲 条件概率、乘法公式、全概率公式
• 引例 10个产品中有7个正品、3个次品, 从中不放回地抽取两个, 已知第一个取到 次品,求第二个又取到次品的概率.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
记 A={从1号箱取得白球},
B ={从2号箱取得红球}
12
Ch2
定义
设 A, B 是两个事件,且 P( A) 0, 称 P(B A) P( AB) P( A)
为事件 A 发生的条件下事件 B 发生的概率,
简)
为事件 B 发生的条件下事件 A发生的概率, 简称A对B的条件概率.
Ch2
用乘法公式容易求出 P(W1W2R3R4) =P(W1)P(W2|W1)P(R3|W1W2)P(R4|W1W2R3)
b bc r rc brbrcbr2 cbr3 c
当 c > 0 时,由于每次取出球后会增加下一次 也取到同色球的概率. 这是一个传染病模型. 每次 发现一个传染病患者,都会增加再传染的概率.
Ch2
条件概率 P(B|A) 的计算
1) 缩减样本空间: 将 缩减为A=A, 采用古典概型来计算.
2) 用定义: P ( B A) P ( A B )
P ( A)
Ch2
条件概率P(BA)与概率P (AB)有何不同?
条件概率P(B|A) 中,A与B地位不同,且已知A 已发生作为条件。在概率P(AB)中,A,B同时 发生,地位相同。在应用时必须区别是 P(BA)还是P(AB)
Ch2
乘法公式应用举例
波里亚罐子模型
b个白球, r个红球
一个罐子中包含b个白球和r个红球. 随机地 抽取一个球,观看颜色后放回罐中,并且再加进 c 个与所抽出的球具有相同颜色的球. 这种手续进行 四次 ,试求第一、二次取到白球且第三、四次取 到红球的概率.
例如从6个正品2个次品的袋中,无放回抽 取2次,一次取一个。A={第一次为正品}, B={第二次为次品},求(1)第二次才取 到次品的概率(2)已知第一次取到正品, B发生的概率。
Ch2
性质
条件概率是概率
(1 )非: 负 P (B A 性 )0 ;
( 2 )规 范 性 :P ( A ) 1 ,P ( A ) 0 ;
P A1A2A3 P A 1 P A 2 |A 1 P A 3 |A 1 A 2
11 211701190
3 200
.
Ch2
波里亚罐子(传染病)模型
b个白球, r个红球
一个罐子中包含b个白球和r个红球. 随机地抽取 一个球,观看颜色后放回罐中,并且再加进 c 个 与所抽出的球具有相同颜色的球. 这种手续进行四 次 ,试求第一、二次取到白球且第三、四次取到 红球的概率.
解:设 A = {活 20 岁以上} , B = {活 25 岁以上}
则有P(BA)P(AB). P(A)
因P 为 (A )0.8, P(B)0.4, P (A) B P (B ), 所以 P(BA)P(AB) 0.4 1.
P(A) 0.8 2
Ch2
乘法公式
利用条件概率求积事件的概率即乘法公式
Ch2
随机取一个球,观看颜色后放 回罐中,并且再加进c个与所抽出
的球具有相同颜色的球.
b个白球, r个红球 解 设 Wi={第i次取出是白球}, i=1,2,3,4
Rj={第j次取出是红球}, j=1,2,3,4 于是W1W2R3R4表示事件“连续取四个球,第一、 第二个是白球,第三、四个是红球. ”
例1 盒中装有5个产品, 其中3个一等品,2个Ch2 二等品, 从中不放回地取产品, 每次1个, 已知 第一次取得一等品,求第二次取得的是二等 品的概率.
解
令
Ai={第
i次取到一等品}, A1
P A2
A1
1 2
(1)
Ch2
例2 某种动物由出生算起活20岁以上的概率为 0.8, 活到25岁以上的概率为0.4, 如果现在有一只 20岁的这种动物, 问它能活到25岁以上的概率是 多少?
(1)
C
(也可直接按古典概型算
1 3
C
1 2
)
C 1C 1
Ch2
( 2 ) P ( A 1A 2 A 3 ) P A 1 P A 2A 1 P A 3A 1 A 2 (2) 213 1 15310430.5 10 3 5
Ch2
例 4 设 某 光 学 仪 器 厂 制 造 的 透 镜 , 第 一 次 落 下 时
打破的1,概 若率 第为 一次,落 第下 二未 次打 落 2
打破的 7,若 概前 率两 是,第 次三 未次 打落 破 破的概9率 1 ,试 0是 求透镜落破 下的 三概 .次率 未
10
解 设 A i透 镜 第 i次 落 下 打 破 ,i1,2,3,
则 A i透 镜 第 i次 落 下 未 打 破 ,i1,2,3,
乘法公式主要用于求几个事件同时发生的概率.
Ch2
例3 盒中装有5个产品, 其中3个一等 品,2个二等品, 从中不放回地取产品, 每次 1个, 求 (1)取两次,两次都取得一等品的概率;
(2)取三次,第三次才取得一等品的概率;
解 令 Ai ={第 i 次取到一等品}
(1 )P (A 1 A 2)P (A 1 )P (A 2A 1 )5 34 2 1 3 0
(1) 若 P(B)>0,则 P(AB) = P(B)P(A|B); 若 P(A)>0,则 P(AB) = P(A)P(B|A).
(2) 若 P(A1A2 ······An1)>0,则 P(A1A2 ······An) = P(A1)P(A2|A1) ······P(An|A1A2 ······An1)
(3 )可 列 可 加 性 :设 B 1 ,B 2 , 是 两 两 互 斥 的 事
件 ,则 有
PBi AP(Bi A).
i1
i1
(4)P(BA)1P(B|A).
( 5 )P [ ( B 1 B 2 ) A ] P [ ( B 1 B 2 ) A ] P ( B 1 A ) P ( B 1 B 2 A ) ;
Ch2
条件概率与乘法公式
问题的提出:
1) 共n张彩票,有3张中彩.
3
问: 第2个人中彩的概率为多少? n
2) 共n张彩票,有3张中彩.
问:已知第l个人摸中,则 第2个人中彩的概率为多少? 2
n 1
Ch2
条件概率与乘法公式
有二个箱子,分别编号为1,2. 1号箱装有1个红球4 个白球,2号箱装有2红3白球. 某人从1号箱中任取一 球放入2号箱,再从2号箱中任意摸出一球, 求已知从1号箱取出白球的条件下从2号箱取得红球 的概率.
