上海宝山区2011年初三数学模拟试卷
上海市宝山区九年级第二学期期中考试数学考试卷(解析版)(初三)中考模拟.doc
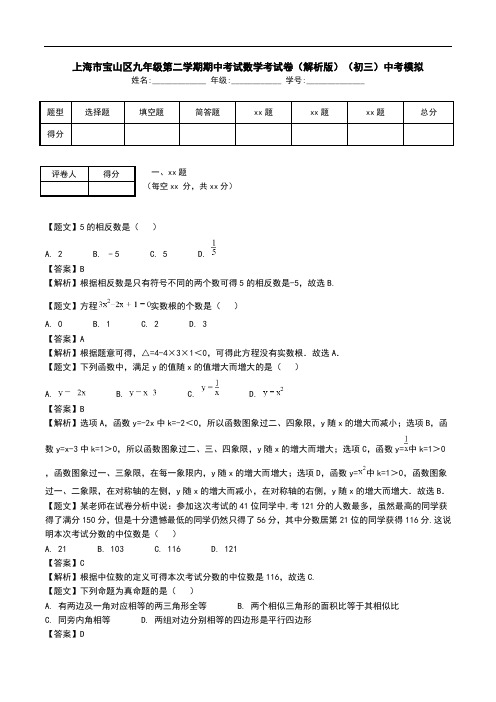
上海市宝山区九年级第二学期期中考试数学考试卷(解析版)(初三)中考模拟姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)【题文】5的相反数是()A. 2B. ﹣5C. 5D.【答案】B【解析】根据相反数是只有符号不同的两个数可得5的相反数是-5,故选B.【题文】方程实数根的个数是()A. 0B. 1C. 2D. 3【答案】A【解析】根据题意可得,△=4-4×3×1<0,可得此方程没有实数根.故选A.【题文】下列函数中,满足y的值随x的值增大而增大的是()A. B. C. D.【答案】B【解析】选项A,函数y=-2x中k=-2<0,所以函数图象过二、四象限,y随x的增大而减小;选项B,函数y=x-3中k=1>0,所以函数图象过二、三、四象限,y随x的增大而增大;选项C,函数y=中k=1>0,函数图象过一、三象限,在每一象限内,y随x的增大而增大;选项D,函数y=中k=1>0,函数图象过一、二象限,在对称轴的左侧,y随x的增大而减小,在对称轴的右侧,y随x的增大而增大.故选B.【题文】某老师在试卷分析中说:参加这次考试的41位同学中,考121分的人数最多,虽然最高的同学获得了满分150分,但是十分遗憾最低的同学仍然只得了56分,其中分数居第21位的同学获得116分.这说明本次考试分数的中位数是()A. 21B. 103C. 116D. 121【答案】C【解析】根据中位数的定义可得本次考试分数的中位数是116,故选C.【题文】下列命题为真命题的是()A. 有两边及一角对应相等的两三角形全等B. 两个相似三角形的面积比等于其相似比C. 同旁内角相等D. 两组对边分别相等的四边形是平行四边形【答案】D【解析】选项A,根据两边及夹角对应相等的两三角形全等,此选项错误;选项B,两个相似三角形的面积比等于其相似比开方,此选项错误;选项C,两直线平行,同旁内角互补,此选项错误;选项D,两组对边分别相等的四边形是平行四边形,此选项正确.故选D.【题文】如图,△ABC中,点D、F在边AB上,点E在边AC上,如果DE∥,EF∥CD,那么一定有()A. B.C. D.【答案】B【解析】由DE∥BC可得,再由EF∥CD可得,所以,即可得,故选B.【题文】计算:______.【答案】【解析】根据有理数的除法法则可得原式= .【题文】计算:=________.【答案】【解析】利用完全平方公式展开可得原式=.【题文】计算:=______.【答案】【解析】原式= .【题文】方程的解是______.【答案】【解析】解得x=1或0,x=1不和题意,舍去,所以x=0.【题文】如果正比例函数的图像经过原点和第一、第三象限,那么______.【答案】【解析】由正比例函数y=(k-1)x的图像经过原点和第一、第三象限可得k-1>0,解得k>1.【题文】二次函数图像的对称轴是直线______.【答案】【解析】二次函数图像的对称轴是直线 .【题文】一枚(形状为正方体的)骰子可以掷出1、2、3、4、5、6这六个数中的任意一个,用这个骰子随机掷出的一个数替代二次根式中的字母x,使该二次根式有意义的概率是________.【答案】【解析】由二次根式有意义可得x-3≥0,即可得x≥3,一枚(形状为正方体的)骰子可以掷出1、2、3、4、5、6这六个数中能使二次根式有意义的结果有3、4、5、6四种情况,所以二次根式有意义的概率是 .【题文】为了解某中学九年级学生的上学方式,从该校九年级全体300名学生中,随机抽查了60名学生,结果显示有5名学生“骑共享单车上学”.由此,估计该校九年级全体学生中约有_______名学生“骑共享单车上学”.【答案】25【解析】由题意可得,该校九年级全体学生中约有300× =25名学生“骑共享单车上学”.【题文】已知在△ABC中,点M、N分别是边AB、AC的中点,如果,,那么向量=______(结果用、表示).【答案】【解析】∵M、N是△ABC的边AB和AC的中点,,,∴, .∵,∴.【题文】如图,在□ABCD中,以点为圆心,以任意长为半径作弧,分别交于点,再分别以为圆心,以大于的长为半径作弧,两弧在内交于点M,连接BM并延长交AD于点E,则DE的长为_________.【答案】2【解析】试题分析:依题意,可知,BE为角平分线,所以,∠ABE=∠CBE,又AD∥BC,所以,∠AEB=∠CBE,所以,∠AEB=∠ABE,AE=AB=3, AD=BC=5,所以,DE=5-3=2。
上海市宝山区、嘉定区2011学年第二学期初三数学二模试卷附答案1

上海市宝山区、嘉定区2011学年中考预测数学试卷(测试时间:100分钟,满分150分) 2012.4. 考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.3.考试不使用计算器.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确的代号填涂在答题纸的相应位置上】 1.下列计算正确的是 ( ).(A )422a a a =+; (B )236a a a =÷; (C )32a a a =⋅; (D )532)(a a =. 2.如果b a <,0<c ,那么下列不等式成立的是( ).(A )c b c a +<+; (B ) c b c a +-<+-; (C )bc ac <; (D )cbc a <. 3.一次函数1-=x y 的图像不.经过( ). (A )第一象限; (B )第二象限; (C )第三象限; (D )第四象限.4.在研究反比例函数图像与性质时,由于计算粗心,小明误认为(2-,3)、(2,3-)、(2-,3-)、 (3,2-)、(23-,4)五个点在同一个反比例函数的图像上,后来经检查发现其中有一个点不在, 这个点是( ).(A )(2,3-); (B )(2-,3); (C )(2-,3-); (D )(23-,4). 5.如图1,在编号为错误!未找到引用源。
、错误!未找到引用源。
、错误!未找到引用源。
、错误!未找到引用源。
的四个三角形中,关于x 轴对称的两个三角形是( ).(A )错误!未找到引用源。
和错误!未找到引用源。
; (B )错误!未找到引用源。
和错误!未找到引用源。
; (C )错误!未找到引用源。
宝山2011年九年级数学模拟测试评分参考

宝山2011年九年级数学模拟测试评分参考一、1. A ; 2. D ; 3. B ; 4. A ; 5. C ; 6. B.二、7. 3a ; 8. m ; 9. )31)(31(--+-x x ; 10. 1-=x ;11.32; 12. 20<<k ; 13. 12-=x y ; 14. 32; 15. 41; 16. 4; 17. 3:1; 18. )1,2(-. 三、19.解:原式=2362324+--- (5分)=)23(6322--- (2分)=3223322+-- (2分)=232- (1分)20.解(1)设正比例函数的解析式为x k y 1=,反比例函数的解析式为xk y 2= (1分) 根据题意得:241⨯=k ,242k =(2分) 解得:21=k ,82=k所以,正比例函数的解析式为x y 2=,反比例函数的解析式为x y 8=. (2分) (2)因为点C (4,n )在反比例函数x y 8=的图像上 所以,248==n ,即点C 的坐标为)2,4( (1分) 因为AO ∥BC ,所以可设直线BC 的表达式为b x y +=2 (1分)又点C 的坐标为)2,4(在直线BC 上所以,b +⨯=422,解得6-=b ,直线BC 的表达式为62-=x y (1分)直线BC 与x 轴交于点B ,设点B 的坐标为)0,(m可以得:620-=m ,解得3=m ,所以点B 的坐标为)0,3( (1分)∴ 5=BC ……………………1分21.解:(1)过点A 作AH ⊥BC ,垂足为H (1分)∵AC AB = ∴BC HC BH 21== (1分) 设x CD AC AB ===∵6=BD∴6+=x BC , 26+=x BH (1分) 在Rt △AHB 中,ABBH ABC =∠cos ,又54cos =∠ABC ∴5426=+x x (2分) 解得:10=x ,所以10=AB (1分)(2)821===BC HC BH 2810=-=-=CH CD DH (1分)在Rt △AHB 中,222AB BH AH =+,又10=AB ,∴6=AH (1分)在Rt △AHD 中,326tan ===∠DH AH ADC∴ADC ∠的正切值是3 (2分)22.证明:(1)∵四边形ABCD 和BEFG 是正方形∴CB AB =,BE BG =,︒=∠=∠90CBE ABG (3分)∴△ABG ≌△CBE (1分)∴CE AG = (1分)(2)∵PG ∥BE ∴CB CG BE PG =,CEPE CB BG = (2分)∵BE BG =,CE AG = ∴CB BG CG PG =,AGPE CB BG = (2分) ∴AGPE CG PG = (1分)23.(1)20 (2分), 3 (2分);(2)由题意:该班女生对“两会”新闻的“关注指数”为%65%1002013=⨯ (1分) 所以,男生对“两会”新闻的“关注指数”为%60 (1分)设该班的男生有x 人则 %60)631(=++-xx (1分), 解得:25=x (1分) 答:该班级男生有25人.(3)该班级女生收看“两会”新闻次数的平均数为3202554635221=⨯+⨯+⨯+⨯+⨯, (2分) 女生收看“两会”新闻次数的方差为:101320)53(2)43(5)33(6)23(5)13(222222=-+-+-+-+- 因为2>1013,所以男生比女生的波动幅度大. (2分) 24.解:(1)由题意得:点B 的坐标为),0(c ,其中0>c ,c OB = (1分)∵OB OA =,点A 在x 轴的负半轴上,∴点A 的坐标为)0,(c - (1分)∵点A 在抛物线c bx x y ++-=2上,∴c bc c +--=20 (1分)∴ 1=+c b (因为0>c ) (1分)(2)∵四边形OABC 是平行四边形∴c AO BC ==,又BC ∥x 轴,点B 的坐标为),0(c∴点C 的坐标为),(c c (1分)又点C 在抛物线上,∴c bc c c ++-=2 ∴0=-c b 或0=c (舍去) (1分) 又 由(1)知:1=+c b∴21=b ,21=c . 抛物线的解析式为21212++-=x x y . (2分) (3)过点P 作⊥PM y 轴,⊥PN BC ,垂足分别为M 、N∵ BP 平分CBO ∠ ∴ PN PM = (1分)设点P 的坐标为)2121(2++-x x x ,∴ x x x =++--)2121(212 (1分) 解得:23=x 或0=x (舍去) (1分)所以,点P 的坐标为)21,23(- (1分) 25.(1)图画正确 (1分)过点M 作AC MN ⊥,垂足为N ∴y NC AN 21== 由题意得:AB PM ⊥, 又AB 是圆O 的直径 ∴1==OP OA ∴︒=∠45APO , 2=PA ∴y PN 212+= (1分) 在Rt △PNM 中,PM PN NPM =∠cos 又x PM +=1,︒=∠45NPM∴ 22121245cos =++=︒x y ∴ y 关于x 的函数解析式为22-=x y (1>x ) (2分)(2)设圆M 的半径为r 因为 OA ⊥MA ,∴∠OAM=90°,12+=r OM又△OMA 与△PMC 相似,所以△PMC 是直角三角形。
宝山区初三数学模拟试卷

一、选择题(每题3分,共30分)1. 下列各数中,绝对值最小的是()A. -3B. 2C. -2D. 02. 若a、b、c是等差数列,且a+b+c=12,a+c=8,则b的值为()A. 4B. 5C. 6D. 73. 下列各式中,正确的是()A. $a^2 - b^2 = (a+b)(a-b)$B. $a^2 + b^2 = (a+b)^2$C. $a^2 - b^2 = (a-b)^2$D. $a^2 + b^2 = (a-b)^2$4. 已知函数$f(x) = 2x + 3$,则$f(-1)$的值为()A. -1B. 1C. 0D. 25. 在直角坐标系中,点A(2,3)关于y轴的对称点坐标为()A.(-2,3)B.(2,-3)C.(-2,-3)D.(2,3)6. 已知等腰三角形ABC中,AB=AC,底边BC=6cm,则腰长AC的长为()A. 3cmB. 4cmC. 5cmD. 6cm7. 若直线y=kx+1与圆x^2+y^2=1相切,则k的值为()A. 0B. 1C. -1D. ±18. 下列命题中,正确的是()A. 若a>b,则a^2>b^2B. 若a>b,则|a|>|b|C. 若a>b,则|a|<|b|D. 若a>b,则a^2<|b|9. 已知函数$y = -\frac{1}{2}x^2 + 3x - 2$,则函数的顶点坐标为()A.(1,4)B.(2,3)C.(3,4)D.(2,1)10. 在等腰三角形ABC中,AB=AC,若∠BAC=45°,则∠B的度数为()A. 45°B. 90°C. 135°D. 180°二、填空题(每题3分,共30分)11. 若a、b、c成等差数列,且a+b+c=12,a+c=8,则b=______。
12. 若$f(x) = 2x + 3$,则$f(0) = ______$。
宝山初三数学模拟试卷

一、选择题(每题3分,共30分)1. 下列选项中,不是一元二次方程的是()A. x^2 - 5x + 6 = 0B. 2x^2 + 3x - 1 = 0C. 3x + 4 = 0D. x^2 + 2x + 1 = 02. 若a > b,那么下列不等式中正确的是()A. a - b > 0B. a + b > 0C. ab > 0D. a/b > 03. 在直角坐标系中,点P(2, -3)关于x轴的对称点坐标是()A. (2, 3)B. (-2, 3)C. (2, -3)D. (-2, -3)4. 若一个正方形的对角线长为10cm,则该正方形的面积是()A. 50cm^2B. 100cm^2C. 25cm^2D. 20cm^25. 下列函数中,不是一次函数的是()A. y = 2x + 3B. y = 5x - 7C. y = 3x^2 + 2D. y = -x + 46. 若sinA = 0.6,且A是锐角,则cosA的值约为()A. 0.8B. 0.4C. 0.2D. 0.17. 下列关于三角形的外角定理的说法正确的是()A. 一个三角形的外角等于其相邻的两个内角之和B. 一个三角形的外角等于其两个不相邻的内角之和C. 一个三角形的外角等于其一个内角D. 一个三角形的外角等于其两个内角之差8. 若等腰三角形的底边长为6cm,腰长为8cm,则该三角形的面积是()A. 24cm^2B. 30cm^2C. 32cm^2D. 36cm^29. 下列关于实数的大小关系,正确的是()A. 3/2 > 2/3B. 2/3 < 1/2C. 3/2 = 2/3D. 3/2 < 2/310. 若一个数的平方根是-3,那么这个数是()A. 9B. -9C. 0D. 无解二、填空题(每题5分,共25分)11. 若一个数的倒数是1/5,则这个数是__________。
12. 在直角三角形中,若一个锐角的正弦值是0.5,则这个角的度数是__________。
2011中考数学考前模拟题及答案精选10套试题试卷_7

2011年中考模拟试卷数学卷考生须知:1.本试卷分试题卷和答题卷两部分。
满分120分,考试时间120分钟。
2.答题前,必须在答题卷的密封区内填写校名、班级、学号、姓名、试场号、座位号。
3.所有答案都必须做在答题卷标定的位置上,务必注意试题序号和答题序号相对应。
4.考试结束后,只需上交答题卷。
一、仔细选一选(本题10小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确的选项前的字母填在答卷中的相应的格子内,注意可以用多种不同的方法来选取正确的答案。
1.2011年3月5日第十一届全国人民代表大会第四次会议在京召开,会议期间议案560多件,提案5762件,充分体现了广大政协委员为发展社会主义民主、推动科学发展、促进社会和谐建言献策的政治责任感。
用科学计数法表示收到的提案数量(保留2个有效数字)( ▲ ) (原创) A . B . C . D . 2.如图1,给你用一副三角板画角,不可能画出的角的度数是: ( ▲ )(原创)A .105°B .75°C .155°D .165° 3.现给出下列四个命题:①无公共点的两圆必外离②位似三角形是相似三角形③菱形的面积等于两条对角线的积④三角形的三个内角中至少有一内角不小于60⑤对角线相等的四边形是矩形其中选中是真命题的个数的概率是( ▲ )(原创)A .51 B .52 C .53 D .544.一个几何体是由一些大小相同的小正方块摆成的,三视图如图所示,则组成这个几何体的小正方块有( ▲ )(原创) A 、4个 B 、5个 C 、6个 D 、7个5.已知线段a 和锐角α∠ ,求作ABC Rt ∆ ,使它的一边为a ,一锐角为α∠ ,满足上述条件的大小不同的可以画这样的三角形( ▲ )。
(原创)A .1个B .2个C .3个D .4个6.在平行四边形ABCD 中,E 为CD 上一点,DE:EC=1:2,连接AE 、BE 、BD ,且AE 、BD 交于点F ,则=∆∆∆ABF EBF DEF S S S ::( ▲ )(原创) A .1:3:9 B .1:5:9 C .2:3:5 D .2:3:93107.5⨯3108.5⨯41057.0⨯310762.5⨯图1BCAE 1E 2 E 3D 4D 1D 2D 3(第10题图)7. 已知点A 的坐标为(2,3),O 为坐标原点,连结OA ,将线段OA 绕点O 按逆时针方向旋转900得OA 1,再将点A 1作关于X 轴对称得到A 2,则A 2的坐标为( ▲ )(原创) A .(-2,3)B .(-2,-3)C .(-3,2)D .(3, 2)8. 给出下列命题:①反比例函数xy 2=的图象经过一、三象限,且y 随x 的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(右图);④相等的弧所对的圆周角相等.其中正确的是( ▲ )(习题摘录改编) (A )③④ (B )①②③ (C )②④ (D )①②③④9.如图,两个反比例函数y = k 1x和y = k 2x在第一象限内的图象依次是C 1和C 2,设点P 在C 1上,PC ⊥x 轴于点C ,交C 2于点A ,PD ⊥y 轴于点D ,交C 2于点B ,则四边形PAOB的面积为( ▲ )(改编)A .k 1+k 2B .k 1-k 2C .k 1·k 2 D.k 1k 210. 如图,已知Rt ABC △,1D 是斜边AB 的中点,过1D 作11D E AC ⊥于E 1,连结1BE 交1CD 于2D ;过2D 作22D E AC ⊥于2E ,连结2BE 交1CD 于3D ;过3D 作33D E AC ⊥于3E ,…,如此继续,可以依次得到点45D D ,,…,n D ,分别记112233BD E BD E BD E △,△,△,…,n n BD E △的面积为123S S S ,,,…n S .则A .n S =14n ABC S △B .n S =13n +ABC S △ C .n S =()121n +ABC S △ D .n S =()211n +ABC S △ ( ▲ )(习题摘录)A 、6B 、62C 、24D 、4 二、认真填一填(本题有6个小题,每小题4分,共24分) 要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案。
宝山区2011学年第一学期九年级数学一模试卷(0113)
2011学年第一学期期末考试九年级数学试卷(满分150分,考试时间100分钟)考生注意:1. 本试卷含四个大题,共26题;2. 考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效; 3. 除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一. 选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是符合题目要求的,请把符合题目要求的选项的代号填涂在答题纸的相应位置上.】 1.下列各式中,正确的是( ▲ ). (A )4222a a a =+; (B )a a a =-23; (C )532a a a =⋅;(D )222)(b a b a +=+.2.下列各数中,是无理数的为( ▲ ).(A )6; (B )38; (C )0π; (D )︒60cos . 3.关于二次函数122+-=x y 的图像,下列说法中,正确的是( ▲ ). (A )对称轴为直线1=x ; (B )顶点坐标为(2-,1);(C )可以由二次函数22x y -=的图像向左平移1个单位得到; (D )在y 轴的左侧,图像上升,在y 轴的右侧,图像下降.4.已知△ABC ∽△DEF ,顶点A 、B 、C 分别与D 、E 、F 对应,若△ABC 和△DEF 的周长 分别为24、36,又BC =8,则下列判断正确的是( ▲ ).(A )12=DE ; (B )12=EF ; (C )18=DE ; (D )18=EF . 5.飞机在空中测得地面上某观测目标A 的俯角为α,且飞机与目标A 相距12千米,那么这时飞机离地面的高度为( ▲ ).(A )αsin 12; (B )αcos 12; (C )αtan 12; (D )αcot 12. 6.下列关于向量的说法中,不.正确..的是( ▲ ). (A )33a a = ; (B )3()33a b a b +=+;(C )若b k a =(k 为实数),则a ∥b ; (D )若b a 3=,则b a 3=或b a 3-=.二.填空题:(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置】 7.计算:=-23▲ .8.已知向量a 、x 满足x a x a +=-)(31,则x = ▲ .(用向量a 表示) 9.分解因式:=-+224x x ▲ .10.已知抛物线1)1(2+-=x a y 的顶点是它的最高点,则a 的 取值范围是 ▲ .11.如图1,已知抛物线2x y =,把该抛物线沿y 轴方向平移,若平移后的抛物线经过点A (2,2),那么平移后的抛物线 的表达式是 ▲ .12.已知抛物线222++-=x x y 的顶点为A ,与y 轴交于点B ,C 是其对称轴上的一点,O 为原点,若四边形ABOC 是等腰 梯形,则点C 的坐标为 ▲ .13.如图2,已知平行四边形ABCD ,E 是边AB 的中点,联结AC 、DE 交于点O . 则OCAO的值为 ▲ . 14.已知一个斜坡的坡角为α,坡度为3:1,则αcot 的值为 ▲ .15.如图3,ABC ∆中,点D 、E 、F 分别在边BC 、AC 、AB 上,且DE ∥AB ,DF ∥AC ,若2:1:=DC BD ,ABC ∆的面积为92cm ,则四边形AEDF 的面积为 ▲ 2cm . 16.如图4,已知梯形ABCD 中,AB ∥CD ,AB ⊥BC ,且AD ⊥BD ,若AB =3,CD=1,那么A ∠的正弦值为 ▲ .17.如图5,已知△ABC 中,点D 、E 分别在边AB 、AC 上,且DB AD 2=,EC AE =.若设a AB =,b BC =,则DE = ▲ .(用向量a 、b 表示) 18.已知△ABC 中,∠C=90°,AB=9,32cos =A ,把△ABC 绕着点C 旋转,使得点A 落在点A ’,点B 落在点B ’. 若点A ’在边AB 上,则点B 、B ’的距离为 ▲ . 三、(本大题共6题,第19--22题,每题8分;第23、24题,每题10分.满分52分) 19.先化简,再求值: )111()1112(2+-÷---+a a a a a ,其中2=a . 20.已知432z y x ==, (1) 求zyx 2-的值; (2) 若y z x -=+3,求x 值.ADBCEO(图2)Ay2O 112 3 x(图1)ADBCE (图5)ADBCF E(图3)(图4)ABCD21.已知一个二次函数的图像经过点A (-1,0)、B (0,3),且对称轴为直线1=x , (1) 求这个函数的解析式;(2) 指出该函数图像的开口方向和顶点坐标,并说明图像的变化情况.22.如图6,已知△ABC 中,AB=AC ,点E 、F 在边BC 上, 满足∠EAF=∠C ,求证:BF·CE= AB 2;23.如图7,已知△ABC 的边BC 长15厘米,高AH 为10厘米,长方形DEFG 内接于△ABC ,点E 、F 在边BC 上,点D 、G 分别在边AB 、AC 上. (1) 设x DG =,长方形DEFG 的面积为y ,试求y 关于x 的函数解析式,并写出定义域;(2) 若长方形DEFG 的面积为36,试求这时AB AD 的值.24.据新华社12月13日电,参加湄公河联合巡逻执法的中国巡逻船顺利返航.已知在巡逻过程中,某一天上午,我巡逻船正在由西向东匀速行驶,10:00巡逻船在A 处发现北偏东53.1°方向,相距10海里的C 处有一个不明物体正在向正东方向移动,10:15巡逻船在B 处又测得该物体位于北偏东18.4°方向的D 处.若巡逻船的速度是每小时36海里, (1) 试在图8中画出点D 的大致位置,并求不明物体移动的速度;(2) 假设该不明物体移动的方向和速度保持不变,巡逻船航行的方向和速度也不变, 试问什么时间该物体与我巡逻船之间的距离最近?【 备用数据:8.01.53sin =︒, 6.01.53cos =︒, 75.01.53cot =︒;32.04.18sin =︒, 95.04.18cos =︒, 34.18cot =︒;】ABCEF(图6)GCHDFE AB(图7)北东ACB(图8)四、(本大题共2题,第25题12分,第26题14分,满分26分) 25.(本题共3小题,4分+5分+3分,满分12分)我们知道,互相垂直且有公共原点的两条数轴构成平面直角坐标系.如果坐标系中两条坐标轴不垂直,那么这样的坐标系称为“斜坐标系”.如图9,P 是斜坐标系xOy 中的任意一点,与直角坐标系相类似,过点P 分别作两坐标轴的平行线,与x 轴、y 轴交于点M 、N ,若M 、N 在x 轴、y 轴上分别对应实数a 、b ,则有序数对(a ,b )叫做点P 在斜坐标系xOy 中的坐标.(1) 如图10,已知斜坐标系xOy 中,∠xOy=60°,试在该坐标系中作出点A (-2,2), 并求点O 、A 之间的距离;(2) 如图11,在斜坐标系xOy 中,已知点B (4,0)、点C (0,3),P (x ,y )是线段BC 上的任意一点,试求x 、y 之间一定满足的一个等量关系式;(3) 若问题(2)中的点P 在线段BC 的延长线上,其它条件都不变,试判断上述x 、y 之间的等量关系是否仍然成立,并说明理由.26.(本题共3小题,3分+6分+5分,满分14分)如图12,已知线段AB ,P 是线段AB 上任意一点(不与点A 、B 重合),分别以AP 、BP 为边,在AB 的同侧作等边△APD 和△BPC ,联结BD 与PC 交于点E ,联结CD . (1) 当BC ⊥CD 时,试求∠DBC 的正切值;(2) 若线段CD 是线段DE 和DB 的比例中项,试求这时PBAP的值; (3) 记四边形ABCD 的面积为S ,当P 在线段AB 上运动时,S 与BD 2是否成正比例, 若成正比例,试求出比例系数;若不成正比例,试说明理由.xPy NOM(图9)x-1y1O 1(图10)xP (x ,y )y COB (图11)ABPCDE(图12)ABPCDE(备用图)宝山区2011学年第一学期期末考试九年级数学参考答案一、选择题1.C; 2.A; 3.D; 4.B; 5.A; 6.D. 二、填空题7.91; 8.a 21-; 9.)1)(1)(2(2-++x x x ; 10.1>a ; 11.22-=x y ;12.)1,1(-; 13.21; 14.3; 15.4; 16. 33; 17. b a 2161+-; 18. 54。
最新初中中考数学题库 2011数学上海宝山模拟卷试卷
宝山区2010年九年级学业模拟考试数学试题(满分: 150 分,考试时间:100分钟)考生注意:1.答题时,考生务必按答题要求在答题纸规定的位置上作答,在本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题:(本大题共6题,每题4分,满分24分)[每小题只有一个正确选项,在答题纸的相应题号的选项上用2 B 铅笔填涂] 1.下列运算正确的是( ▲ )(A) 10a ÷52a a = (B) 422a a a =+ (C) 222)(b a b a +=+ (D) 632)(a a =2.1=x 是下列哪个方程的解?( ▲ )(A) 1112-=-x x x (B) x x -=23(C) 01=+x (D) 1=+y x 3.下列不等式组中,解集为12<≤-x 的是( ▲ ) (A) ⎩⎨⎧>-≥+0102x x (B) ⎩⎨⎧<-≥-0102x x (C) ⎩⎨⎧>-≥+0102x x (D) ⎩⎨⎧>-≥-0102x x4.已知0<k ,0>b ,那么一次函数b kx y +=的大致图像是( ▲ )5.已知四边形ABCD ,下列条件中,不.能确定四边形ABCD 是平行四边形的是( ▲ ) (A) AB ∥CD 且AD ∥BC ; (B) AB ∥CD 且 AB = CD ; (C) AB ∥CD 且AD = B C ; (D) AB ∥CD 且C A ∠=∠. 6.已知两个相似三角形的相似比是1︰2,则下列判断中,错误..的是( ▲ ) (A) 对应边的比是1:2; (B) 对应角的比是1:2; (C) 对应周长的比是1:2; (D) 对应面积的比是1:4; 二、填空题:(本大题共12题,每题4分,满分48分)Oyx(A)Oyx(C)Oyx(B)Oyx(D)[请将结果直接填入答题纸的相应位置] 7.计算:=-219▲ .8.因式分解:a a 43-= ▲ .9.用配方法解方程261x x -=时,方程的两边应该同加上 ▲ ,才能使得方程左边 配成一个完全平方式.10.经过点A (2, 1)且与直线y x =-平行的直线表达式为 ▲ . 11.解方程2232=---x x x x 时,如果设y xx =-2,那么原方程可以化为关于y 的整式方程.这个整式方程是 ▲ .12.某公司承担了制作600个上海世博会道路交通指引标志的任务, 原计划x 天完成,实际平均每天多制作了10个,因此提前5天完成任务。
上海宝山区2009年初三数学中考模拟试卷含参考答案及评分标准
2009年宝山区初三模拟测试数学试卷(满分150分,考试时间100分钟) 2009.4.考生注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分) 【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】 1.4的平方根是(A )2; (B )2-; (C )2±; (D )2±.2.下列等式中,一定成立的是(A )222)(b a b a +=+; (B )3232a a a =+;(C )aa2121=-; (D )523a a a =⋅. 3.1=x 是下列哪个方程的解(A)01=+x ; (B)1112-=-x x x ; (C)1=+y x ; (D)0433=-+x x . 4.已知点A (-2,3 )在双曲线xky =上,则下列点中,一定在该双曲线上的点是 (A )A (3,-2 ); (B )A (-2,-3 ); (C )A (2,3 ); (D )A (3,2) . 5.下列图形中,是旋转对称图形,但不是中心对称图形的是(A )等腰梯形; (B )等边三角形; (C )平行四边形; (D )直角梯形.6.在研究圆的有关性质时,我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条 直径翻折,可以看到直径两侧的两个半圆互相重合”。
由此说明:(A)圆是中心对称图形,圆心是它的对称中心;(B)圆是轴对称图形,任意一条直径所在的直线都是它的对称轴; (C)圆的直径互相平分;(D)垂直弦的直径平分弦及弦所对的弧.一、填空题:(本大题共12题,每题4分,满分48分) [请将结果直接填入答题纸的相应位置] 7.计算:28-= ▲ .8.因式分解:a a 2213-= ▲ .9.方程21=-x 的解为 ▲ .10.已知一次函数y=kx+b 的图象经过点A (2,1)(如图1), 当x ▲ 时,y ≥1.11.从1、2、3、…… 9九个自然数中任选一个数,选出的数被2整除的概率是 ▲ .12.小明家离开学校的距离是a 米,他上学时每分钟走b 米,放学回家时每分钟比上学时少走 15米,则小明从学校回家用的时间是 ▲ 分钟(用含a 、b 的代数式表示). 13.请你写出一个..二次函数解析式,使其图像的顶点在y 轴上,且在y 轴右侧图像是下降的。
2010学年宝山区第二学期九年级数学模拟测试试卷2011.4(扫描版,无答案)
新世纪教育网精选资料 版权全部 @新世纪教育网2010 学年第二学期奉贤区调研测试九年级数学试卷 2011. 04( 完卷时间 100 分钟,满分 150 分 )考生注意:1.本试卷含三个大题,共 25 题.2.答题时,考生务必按答题要求在答题纸 规定的地点上作答,在底稿纸、本试卷上答题一...律无效.3.除第一、二大题外,其他各题如无特别说明,都一定在答题纸 ...的相应地点上写出证明或 计算的主要步骤.一、选择题:(本大题共 6 题,每题 4 分,满分 24 分) 1.计算 a 3 a 2 的结果是(▲ )A . a 5 ;B . a 6 ;C . a 8 ;D . a 9 .2.以下运算不正确的选项是( ▲ )A .(2)2 2;B .2 3 6; C .6 2 3; D . 2 3 5.3.如图,直线 CD 是线段 AB 的垂直均分线, P 为直线 CD 上的一点,已知线段PA = 5,那么线段 PB 的长度为( ▲ )A .3;B .4 ;C .5 ;D .6.第3题图4.小悦买书需用48 元钱,付款时恰巧用了 1 元和 5 元的纸币共12 张.设所用的 1 元纸币为 x 张,依据题意,下边所列方程正确的选项是( ▲ )A . 5x (12 x) 48 ;B . x 5(x 12) 48 ;C . x12( x 5)48 ;D . x 5(12x) 48 .5.某种彩票的中奖时机是1%,以下说法正确的选项是(▲)A .买 1 张这类彩票必定不会中奖;B .买 100 张这类彩票必定会中奖;C .买 1 张这类彩票可能会中奖;D .买 100 张这类彩票必定有 99 张彩票不会中奖.6.如图,正方形 ABCD 中,E 为 AB 的中点,AF ⊥DE 于点 O ,那么AO等于( ▲ )DOA .2 5;B .1;C .2;D .1.3332D CFO第6题图AEB二、填空题:(本大题共 12 题,每题 4 分,满分 48 分)7.截止到 2010 年 10 月 31 日,上海世博园共招待旅客73 080 000 人,y 用科学记数法表示是▲人.8.函数y1中,自变量x 的取值范围是▲.x x3O9. 方程 2 x1 2 的根是▲ .第 11题图10.在直角坐标系中,点A(2,-2) 与点 B( 2 ,1) 之间的距离 AB▲.11.已知反比率函数y m2▲ .x的图象以下图,那么 m 的取值范围是12.如图, l1表示某摩托厂一天的销售收入与摩托车销售量之间的关系;l 2表示该摩托厂一天的销售成本与销售量之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011学年第一学期期末考试九年级数学试卷
(满分150分,考试时间100分钟)
考生注意:
1. 本试卷含四个大题,共26题;
2. 考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效; 3. 除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或
计算的主要步骤. 一. 选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是符合题目要求的,请把符合题目要求的选项的代号填涂在答题纸的相应位置上.】 1.下列各式中,正确的是( ▲ ). (A )4
2
2
2a a a =+; (B )a a a =-2
3; (C )5
3
2
a a a =⋅;
(D )2
2
2
)(b a b a +=+.
2.下列各数中,是无理数的为( ▲ ).
(A )6; (B )38; (C )0π; (D )︒60cos . 3.关于二次函数122+-=x y 的图像,下列说法中,正确的是( ▲ ). (A )对称轴为直线1=x ; (B )顶点坐标为(2-,1);
(C )可以由二次函数22x y -=的图像向左平移1个单位得到; (D )在y 轴的左侧,图像上升,在y 轴的右侧,图像下降.
4.已知△ABC ∽△DEF ,顶点A 、B 、C 分别与D 、E 、F 对应,若△ABC 和△DEF 的周长 分别为24、36,又BC =8,则下列判断正确的是( ▲ ).
(A )12=DE ; (B )12=EF ; (C )18=DE ; (D )18=EF . 5.飞机在空中测得地面上某观测目标A 的俯角为α,且飞机与目标A 相距12千米,那么这时飞机离地面的高度为( ▲ ).
(A )αsin 12; (B )αcos 12; (C )αtan 12; (D )αcot 12. 6.下列关于向量的说法中,不.正确..
的是( ▲ ).
(A )3; (B )3()33a b a b +=+
;
(C =k 为实数),则∥; (D =,则3=或3-=.
二.填空题:(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置】 7.计算:=-2
3
▲ .
8.已知向量、x 满足
x a x a +=-)(3
1
,则x = ▲ .
(用向量表示) 9.分解因式:=-+224x x ▲ .
10.已知抛物线1)1(2+-=x a y 的顶点是它的最高点,则a 的 取值范围是 ▲ .
11.如图1,已知抛物线2
x y =,把该抛物线沿y 轴方向平移,
若平移后的抛物线经过点A (2,2),那么平移后的抛物线 的表达式是 ▲ .
12.已知抛物线222++-=x x y 的顶点为A ,与y 轴交于点B ,
C 是其对称轴上的一点,O 为原点,若四边形ABOC 是等腰 梯形,则点C 的坐标为 ▲ .
13.如图2,已知平行四边形ABCD ,E 是边AB 的中点,联结
AC 、DE 交于点O . 则
OC
AO
的值为 ▲ . 14.已知一个斜坡的坡角为α,坡度为3:1,则αcot 的值为 ▲ .
15.如图3,ABC ∆中,点D 、E 、F 分别在边BC 、AC 、AB 上,且DE ∥AB ,DF ∥AC ,
若2:1
:=DC BD ,ABC ∆的面积为92cm ,则四边形AEDF 的面积为 ▲
2cm . 16.如图
4,已知梯形ABCD 中,AB ∥CD ,AB ⊥BC ,且AD ⊥BD ,若AB =3,CD=1,
那么A ∠的正弦值为 ▲ .
17.如图5,已知△ABC 中,点D 、E 分别在边AB 、AC 上,且DB AD 2=,EC AE =.
若设a AB =,b BC =,则DE = ▲ .(用向量、表示) 18.已知△ABC 中,∠C=90°,AB=9,3
2
cos =
A ,把△ABC 绕着点C 旋转,使得点A 落在点A ’,点
B 落在点B ’. 若点A ’在边AB 上,则点B 、B ’的距离为 ▲ . 三、(本大题共6题,第19--22题,每题8分;第23、24题,每题10分.满分52分) 19.先化简,再求值: )1
1
1()1112(2+-÷---+a a a a a ,其中2=a . 20.已知4
32z
y x ==, (1) 求z y x 2-的值; (2) 若y z x -=+3,求x 值.
E
(图2)
D
(图3)
(图4)
A
B
C
D
21.已知一个二次函数的图像经过点A (-1,0)、B (0,3),且对称轴为直线1=x , (1) 求这个函数的解析式;
(2) 指出该函数图像的开口方向和顶点坐标,并说明图像的变化情况.
22.如图6,已知△ABC 中,AB=AC ,点E 、F 在边BC
满足∠EAF=∠C ,求证:BF·CE= AB 2;
23.如图7,已知△ABC 的边BC 长15厘米,高AH 为10厘米,长方形DEFG 内接于△ABC ,
点E 、F 在边BC 上,点D 、G 分别在边AB
、AC 上. (1) 设x DG =,长方形DEFG 的面积为y ,试求
y 关于x 的函数解析式,并写出定义域;
(2) 若长方形DEFG 的面积为36,试求这时AB
AD
的值.
24.据新华社12月13日电,参加湄公河联合巡逻执法的中国巡逻船顺利返航.已知在巡逻
过程中,某一天上午,我巡逻船正在由西向东匀速行驶,10:00巡逻船在A 处发现北偏东53.1°方向,相距10海里的C 处有一个不明物体正在向正东方向移动,10:15巡逻船在B 处又测得该物体位于北偏东18.4°方向的D 处.若巡逻船的速度是每小时36海里, (1) 试在图8中画出点D 的大致位置,并求不明物体移动的速度;
(2) 假设该不明物体移动的方向和速度保持不变,巡逻船航行的方向和速度也不变, 试问什么时间该物体与我巡逻船之间的距离最近?
【 备用数据:8.01.53sin =︒, 6.01.53cos =︒, 75.01.53cot =︒;
32.04.18sin =︒, 95.04.18cos =︒, 34.18cot =︒;】
(图6)
G
C
H
D
F
E A
B
(图7)
北
东
(图8)
四、(本大题共2题,第25题12分,第26题14分,满分26分) 25.(本题共3小题,4分+5分+3分,满分12分)
我们知道,互相垂直且有公共原点的两条数轴构成平面直角坐标系.如果坐标系中两条坐标轴不垂直,那么这样的坐标系称为“斜坐标系”.
如图9,P 是斜坐标系xOy 中的任意一点,与直角坐标系相类似,过点P 分别作两坐标轴的平行线,与x 轴、y 轴交于点M 、N ,若M 、N 在x 轴、y 轴上分别对应实数a 、b ,则有序数对(a ,b )叫做点P 在斜坐标系xOy 中的坐标.
(1) 如图10,已知斜坐标系xOy 中,∠xOy=60°,试在该坐标系中作出点A (-2,2), 并求点O 、A 之间的距离;
(2) 如图11,在斜坐标系xOy 中,已知点B (4,0)、点C (0,3),P (x ,y )是线段BC 上的任意一点,试求x 、y 之间一定满足的一个等量关系式;
(3) 若问题(2)中的点P 在线段BC 的延长线上,其它条件都不变,试判断上述x 、y 之间的等量关系是否仍然成立,并说明理由.
26.(本题共3小题,3分+6分+5分,满分14分)
如图12,已知线段AB ,P 是线段AB 上任意一点(不与点A 、B 重合),分别以AP 、BP 为边,在AB 的同侧作等边△APD 和△BPC ,联结BD 与PC 交于点E ,联结CD . (1) 当BC ⊥CD 时,试求∠DBC 的正切值;
(2) 若线段CD 是线段DE 和DB 的比例中项,试求这时
PB
AP
的值; (3) 记四边形ABCD 的面积为S ,当P 在线段AB 上运动时,S 与BD 2是否成正比例, 若成正比例,试求出比例系数;若不成正比例,试说明理由.
(
图11)
A
B
P
(图
12)
A
B
(备用图)。
