离散数学习题整合
(完整版)离散数学题目及答案

数理逻辑习题判断题1.任何命题公式存在惟一的特异析取范式 ( √ ) 2. 公式)(q p p →⌝→是永真式 ( √ ) 3.命题公式p q p →∧)(是永真式 ( √ ) 4.命题公式r q p ∧⌝∧的成真赋值为010 ( × ) 5.))(()(B x A x B x xA →∃=→∀ ( √ )6.命题“如果1+2=3,则雪是黑的”是真命题 ( × ) 7.p q p p =∧∨)( ( √ )8.))()((x G x F x →∀是永真式 ( × ) 9.“我正在撒谎”是命题 ( × ) 10. )()(x xG x xF ∃→∀是永真式( √ )11.命题“如果1+2=0,则雪是黑的”是假命题 ( × ) 12.p q p p =∨∧)( ( √ )13.))()((x G x F x →∀是永假式 ( × )14.每个命题公式都有唯一的特异(主)合取范式 ( √ ) 15.若雪是黑色的:p ,则q →p 公式是永真式 ( √ ) 16.每个逻辑公式都有唯一的前束范式 ( × ) 17.q →p 公式的特异(主)析取式为q p ∨⌝ ( × ) 18.命题公式 )(r q p →∨⌝的成假赋值是110 ( √ ) 19.一阶逻辑公式)),()((y x G x F x →∀是闭式( × )单项选择题1. 下述不是命题的是( A )A.花儿真美啊! B.明天是阴天。
C.2是偶数。
D.铅球是方的。
2.谓词公式(∀y)(∀x)(P(x)→R(x,y))∧∃yQ(x,y)中变元y (B)A.是自由变元但不是约束变元B.是约束变元但不是自由变元C.既是自由变元又是约束变元D.既不是自由变元又不是约束变元3.下列命题公式为重言式的是( A )A.p→ (p∨q)B.(p∨┐p)→qC.q∧┐q D.p→┐q4.下列语句中不是..命题的只有(A )A.花儿为什么这样红?B.2+2=0C.飞碟来自地球外的星球。
离散数学练习题(含答案)

离散数学练习题(含答案)题目1. 对于集合 $A={1,2,3,...,10}$ 和 $B={n|n是偶数,2<n<8}$,求 $A \cap B$ 的元素。
2. 存在三个可识别的状态A,B,C。
置换群 $S_3$ 作用在状态集上。
定义四个动作:$α: A → C, β: A → B, γ: C→ A, δ: B→ C$。
确定式子,描述 $\{α,β,γ,δ\}$ 的乘法表。
3. 证明 $\forall n \in \mathbb{N}$,合数的个数不小于$n$。
4. 给定一个无向带权图,图中每个节点编号分别是$1,2,...,n$,证明下列结论:a. 如果从节点$i$到$j$只有一条权值最小的路径,则这条路径的任意子路径都是最短路径。
b. 如果从节点$i$到$j$有两条或两条以上权值相等的路径,则从$i$到$j$的最短路径可能不唯一。
答案1. $A \cap B = \{2,4,6\}$。
2. 乘法表:3. 对于任意$n$,我们可以选择$n+1$个连续的自然数$k+1,k+2,...,k+n,k+n+1$中的$n$个数,其中$k \in \mathbb{Z}$。
这$n$个数构成的$n$个正整数均为合数,因为它们都至少有一个小于它自身的因子,所以不是质数。
所以合数的个数不小于任意$n$。
4.a. 根据题意,从$i$到$j$只有一条权值最小的路径,即这条最短路径已被确定。
如果从这条路径中任意取出一段子路径,假设这段子路径不是这个节点到$j$的最短路径,那么存在其他从$i$到$j$的路径比这段子路径更优,又因为这条路径是最短路径,所以这段子路径也一定不优于最短路径,矛盾。
所以从这条路径中任意取出的子路径都是最短路径。
b. 如果从节点$i$到$j$有多条权值相等的路径,则这些路径权值都是最短路径的权值。
因为所有最短路径的权值相等,所以这些路径的权值就是最短路径的权值。
所以从$i$到$j$的最短路径可能不唯一。
离散数学-习题集

离散数学-习题集《离散数学》习题集第⼀部分判断题⼀、第⼀章—集合1、()已知集合A的元素个数为10,则集合A的幂集的基=102。
2、()已知两个集合A、B,若A中的元素都是B中的元素,则记为A∈B。
2、()已知集合A的元素个数为n,则集合A的幂集P(A)的元素个数为n2。
3、( ) 已知两个集合A={Ф,{Ф}},B={Ф},则A∩B={Ф}。
4、()已知两个集合A={Ф,{Ф}},B={Ф},则A∩B=Ф。
5、()已知两个集合A、B,若A中的元素都是B中的元素,则记为A∈B。
6、()已知集合A的元素个数为n,则集合A的幂集P(A)的元素个数为n2。
7、()已知集合A的元素个数为n,则A×A的幂集的元素个数为n2。
8、()已知两个集合A、B,则A-B是由属于B但不属于A的元素构成的集合。
⼆、第⼆章—⼆元关系1、()若R是A上的⼆元关系,I A是A上的恒等关系,则当且仅当I A∈R时,R是A上的⾃反关系。
2、(√)若R是集合A上的⼆元关系,且当(a,b)∈R且(a,c)∈R时,就有(b,c)∈R,则R是A 上的可传递关系。
3、()设A是集合,A1、A2、...A n都是A的⾮空⼦集,令S={A1,A2,...,A n},则如果S是集合A的⼀个划分,那么S⼀定是集合A的⼀个完全覆盖;反之亦然。
5、()R是⾮空集合A上的等价⼆元关系,则A关于R的商集A/R是集合A的⼀个划分,但不是A的⼀个完全覆盖。
6、()已知集合A有4元素,易知集合A共有24个互不相同的⼦集合,所以在集合A上⼀共可定义24个互不相同的⼆元关系。
7、()若R1和R2都是集合A上的可传递⼆元关系,则R1∪R2也是A上的传递关系。
8、()设R是有限的⾮空集合A上的偏序关系,则A必有极⼤(⼩)元和最⼤(⼩)元。
9、()若R1和R2都是集合A上的相容关系,则R1∩R2也是A上的相容关系。
10、()若R1和R2都是集合A的可传递⼆元关系,则R1∩R2也是A上的传递关系。
离散数学试题总汇及答案

离散数学试题总汇及答案一、单项选择题(每题2分,共20分)1. 在集合{1, 2, 3, 4}中,子集{1, 2}的补集是()。
A. {3, 4}B. {1, 3, 4}C. {2, 3, 4}D. {1, 2, 3, 4}答案:A2. 命题“若x > 0,则x² > 0”的逆否命题是()。
A. 若x² ≤ 0,则x ≤ 0B. 若x² > 0,则x > 0C. 若x ≤ 0,则x² ≤ 0D. 若x² ≤ 0,则x < 0答案:C3. 函数f(x) = x² + 2x + 1的值域是()。
A. {x | x ≥ 0}B. {x | x ≥ 1}C. {x | x ≥ 2}D. {x | x ≥ -1}答案:B4. 以下哪个图是无向图()。
A. 有向图B. 无向图C. 有向树D. 无向树答案:B5. 以下哪个图是二分图()。
A. 完全图B. 非完全图C. 任意两个顶点都相连的图D. 任意两个顶点都不相连的图答案:C6. 以下哪个是哈密顿回路()。
A. 经过每个顶点恰好一次的回路B. 经过每个顶点至少一次的回路C. 经过每个顶点恰好两次的回路D. 经过每个顶点至少两次的回路答案:A7. 以下哪个是欧拉回路()。
A. 经过每条边恰好一次的回路B. 经过每条边至少一次的回路C. 经过每条边恰好两次的回路D. 经过每条边至少两次的回路答案:A8. 以下哪个是二进制数()。
A. 1010B. 1020C. 1102D. 1120答案:A9. 以下哪个是格雷码()。
A. 0101B. 1010C. 1100D. 1110答案:B10. 以下哪个是素数()。
A. 4B. 6C. 7D. 8答案:C二、填空题(每题2分,共20分)11. 集合{1, 2, 3}与{2, 3, 4}的交集是______。
答案:{2, 3}12. 命题“若x > 0,则x² > 0”的逆命题是:若x² > 0,则______。
全版离散数学 练习题及答案.ppt

课件
例3 对任意两个集合A, B,试证 A (A B) A B
证明 对于任意的x
x A (A B)
x {x x A x ( A B)} x {x x A (x A B)} x {x x A (x A x B)} x {x x A (x A x B)} x {x x A x B}
课件
例10 求图的最小生成树
A 1B34 Nhomakorabea5
2 E
6
1A 2
B
E
4
6
C7 D
C
D
课件
例11
• 无向树T有7片树叶, 3个3度顶点,其余的 都是4度顶点,则T有几个4度顶点?
• 解:设T有x个4度顶点 顶点度数之和: 7+3*3+4x 由树的性质可得总边数: 7+3+x-1 由握手原理可得: 7+3*3+4x=2(7+3+x-1)
求g f
g f { 1,b , 2,b , 3,b }
课件
例12 求复合函数
X {1,2,3}, Y {p, q}, Z {a,b} f { 1, p , 2, p , 3, q } g { p,b , q,b }
求g f
g f { 1,b , 2,b , 3,b }
课件
例: 求幺元、零元、逆元
x A B 因为 x 是任意的,所以有
x ((x A (A B)) (x A B)) 的真值为T,
因此 A ( A B)课件 A B
例4 判断关系的性质
R1 { a, a , a,b , b,b , c,c }
a
1 1 0
M R 1 0 1 0
0 0 1
离散数学练习题(含答案)

离散数学练习题(含答案)离散数学试题第一部分选择题1.下列命题变元p,q的小项是(C)。
A。
p∧┐p∧qB。
┐p∨qC。
┐p∧qD。
┐p∨p∨q2.命题“虽然今天下雪了,但是路不滑”可符号化为(D)。
A。
p→┐qB。
p∨┐qC。
p∧qD。
p∧┐q3.只有语句“1+1=10”是命题(A)。
A。
1+1=10B。
x+y=10___<0D。
x mod 3=24.下列等值式不正确的是(C)。
A。
┐(x)A(x)┐AB。
(x)(B→A(x))B→(x)A(x)C。
(x)(A(x)∧B(x))(x)A(x)∧(x)B(x)D。
(x)(y)(A(x)→B(y))(x)A(x)→(y)B(y) 5.量词x的辖域是“Q(x,z)→(x)(y)R(x,y,z)”(C)。
A。
(x)Q(x,z)→(x)(y)R(x,y,z))B。
Q(x,z)→(y)R(x,y,z)C。
Q(x,z)→(x)(y)R(x,y,z)D。
Q(x,z)6.设A={a,b,c,d},A上的等价关系R={。
}∪IA则对应于R的A的划分是(D)。
A。
{{a},{b,c},{d}}B。
{{a,b},{c},{d}}C。
{{a},{b},{c},{d}}D。
{{a,b},{c,d}}7.设A={Ø},B=P(P(A)),以下正确的式子是(A)。
A。
{Ø,{Ø}}∈BB。
{{Ø,Ø}}∈BC。
{{Ø},{{Ø}}}∈BD。
{Ø,{{Ø}}}∈B8.集合相对补运算中,不正确的等式是(A)。
A。
(X-Y)-Z=X-(Y∩Z)B。
(X-Y)-Z=(X-Z)-YC。
(X-Y)-Z=(X-Z)-(Y-Z)D。
(X-Y)-Z=X-(Y∪Z)9.在自然数集N上,不可结合的定义的运算是(D)。
A。
a*b=min(a,b)B。
a*b=a+bC。
a*b=GCD(a,b) (a,b的最大公约数)D。
离散数学习题集(十五套)---答案.docx
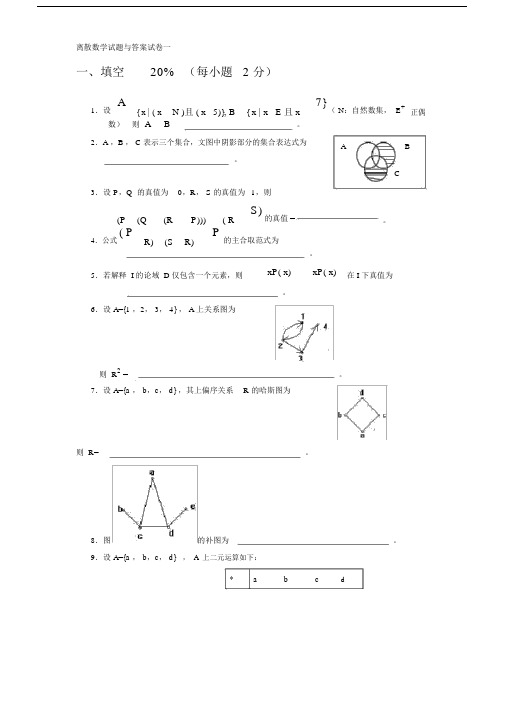
离散数学试题与答案试卷一一、填空20%(每小题 2 分)1.设A{ x | ( x N )且 ( x5)}, B{ x | x E 且 x7}( N:自然数集, E+正偶数)则 A B。
2.A ,B , C 表示三个集合,文图中阴影部分的集合表达式为A B。
C 3.设 P,Q 的真值为0,R, S 的真值为1,则(P(Q(R P)))( R S)的真值 =。
4.公式( PR)(S R)P的主合取范式为。
5.若解释 I 的论域 D 仅包含一个元素,则xP( x)xP( x)在 I 下真值为。
6.设 A={1 ,2, 3, 4} , A 上关系图为则 R2 =。
7.设 A={a , b,c, d} ,其上偏序关系R 的哈斯图为则 R=。
8.图的补图为。
9.设 A={a , b,c, d},A上二元运算如下:*a b c da abc db bcd ac cd a bd d a b c那么代数系统<A ,*> 的幺元是,有逆元的元素为,它们的逆元分别为。
10.下图所示的偏序集中,是格的为。
二、选择20%(每小题 2 分)1、下列是真命题的有()A .{ a}{{ a}};B .{{}}{ ,{ }};C.{{},} ;D.{ }{{}} 。
2、下列集合中相等的有()A . {4 , 3}; B. {,3, 4} ;C. {4 ,, 3,3} ;D . {3 , 4} 。
3、设 A={1 ,2, 3} ,则 A 上的二元关系有()个。
A . 23;B . 32;C. 23 3;D.32 2。
4、设 R,S 是集合 A 上的关系,则下列说法正确的是()A .若 R, S 是自反的,则RS 是自反的;B .若 R, S 是反自反的,则 R S 是反自反的;C.若 R, S 是对称的,则RS 是对称的;D .若 R, S 是传递的,则RS 是传递的。
5、设 A={1 ,2, 3, 4} , P( A )(A 的幂集)上规定二元系如下R{s,t| s,t p( A)(| s || t |}则 P(A ) / R=()A . A; B. P(A) ; C. {{{1}} , {{1 , 2}} , {{1 ,2, 3}} , {{1 , 2, 3, 4}}} ;D. {{} ,{2}, {2 ,3} , {{2 , 3, 4}} , {A}}6、设 A={, {1} , {1 , 3} , {1 , 2, 3}} 则 A上包含关系“”的哈斯图为()7、下列函数是双射的为()A . f : I E , f (x) = 2x;B. f : N N N, f (n) = <n , n+1> ;C. f : R I , f (x) = [x]; D . f :I N, f (x)= | x | 。
离散数学试题总汇及答案

离散数学试题总汇及答案一、单项选择题(每题2分,共20分)1. 在集合{1,2,3}和{3,4,5}的笛卡尔积中,元素(2,4)是否存在?A. 存在B. 不存在C. 无法确定D. 以上都不对2. 函数f: A→B是单射的,当且仅当对于任意的a1, a2∈A,若f(a1)=f(a2),则a1=a2。
A. 正确B. 错误C. 无法确定D. 以上都不对3. 以下哪个命题是真命题?A. 所有的狗都会游泳。
B. 有些狗不会游泳。
C. 所有的狗都不会游泳。
D. 以上都不是真命题。
4. 如果p蕴含q为假,那么p和q的真值可以是?A. p为真,q为假B. p为假,q为真C. p为真,q为真D. p为假,q为假5. 以下哪个图是连通图?A. 一个孤立点B. 两个不相连的点C. 一个包含三个点且每对点都相连的图D. 以上都不是连通图6. 在有向图中,如果存在从顶点u到顶点v的路径,那么称v是u的后继顶点。
A. 正确B. 错误C. 无法确定D. 以上都不对7. 以下哪个等价关系是集合{1,2,3}上的?A. {(1,1), (2,2), (3,3)}B. {(1,2), (2,1), (2,2), (3,3)}C. {(1,1), (2,3), (3,2), (3,3)}D. {(1,1), (2,2), (3,3), (1,3)}8. 以下哪个命题是假命题?A. 所有的鸟都有羽毛。
B. 有些鸟不会飞。
C. 所有的哺乳动物都是温血动物。
D. 以上都不是假命题。
9. 在图论中,一个图的生成树是包含图中所有顶点的最小连通子图。
A. 正确B. 错误C. 无法确定D. 以上都不对10. 如果命题p和q互为逆否命题,那么它们具有相同的真值。
A. 正确B. 错误C. 无法确定D. 以上都不对二、填空题(每题2分,共20分)1. 集合{1,2,3}和{3,4,5}的并集是________。
2. 函数f: A→B是满射的,当且仅当对于任意的b∈B,存在a∈A,使得f(a)=________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CH01复习题§1.21. 命题判断〔每空1分,共4分〕 P32-A 小和小王是同班同学B 小猪不是鲜花C 3-2n<0D 假如2+2=4,如此太阳从西方升起。
上述语句中,是简单命题,不是命题,是符合命题且真值为假,是符合命题且真值为真。
〔参考答案:ACDB 〕2. 命题符号化〔每空2分,共4分〕习题1.5(7)(3) P32-p :天下大雨,q :他乘公共汽车去上班,命题“除非天下大雨,否如此他不乘公共汽车去上班〞可符号化为。
〔参考答案:q →p 必要条件为后件〕r :天很冷,s :老来了,命题“虽然天很冷,老还是来了〞 可符号化为。
〔参考答案r ∧s 〕3. 五个真值表〔每空2分,共4分〕习题1.6(2)(4) P32-设p 的真值为0,r 的真值为1,q 、s 都是命题,如此命题公式〔)()(s q r p ∨⌝∧↔的真值为,命题公式)()))(((s r p r q p ⌝∨→⌝∧→∨⌝的真值为。
〔参考答案:0,1〕4. 用符号p 、q 填空。
〔每空1分,共4分〕根本概念设p :x>0〔其中x 是整数〕 ,q :太阳从西方升起,如此是命题,是命题变项,是命题常项,不是命题。
〔参考答案:q ,p ,q ,p 〕5. 命题符号化,相容或与排斥或设r :现在小在图书馆,s :现在小在学生宿舍,如此“现在小在图书馆或学生宿舍〞可符号化为。
〔参考答案:B 〕A r ∨sB (r ∧¬s)∨(¬r∧s)C r ∧sD (r ∧¬s)或(¬r∧s)§1.2 命题公式与分类:A 是含三个命题变项的命题公式,且A(001)=0,A(100)=1,如此A 是。
〔D 〕A 矛盾是B 可满足式C 重言式D 非重言式的可满足式§1.3 等值演算用等值演算法证明等值式:(p ∧q)→rp →(q →r). (演算的每一步都要写依据)§1.4 式6. A(p,q)的真值表求A 的永主析取式、主合取式、成真赋值和成假赋值。
〔参考答案:m 1∨m 3,M 0∧M 2,01、11,00、10〕7. 〔2分〕命题公式B(p,q,r)=(¬p∧r∧¬q)的主析取式是。
〔参考答案:C〕A m2B M6C m1D M5 E命题公式B(p,q,r)=(¬p∨¬q∨r)的主析取式是。
〔参考答案:A〕A m0∨m1∨m2∨m3∨m4∨m5∨m7B M6C m1D M1§1.5 全功能集〔2分〕不是联结词全功能集。
〔参考答案:D〕A {↑}B {¬,→}C {¬,∨}D {∧,∨}是联结词全功能集。
〔参考答案:A〕A {↓,}B {∨,∧}C {∨}D {∧}§1.6 组合电路〔习题1.16〕有一盏灯由三个开关控制,要求按任何一个开关都能使灯由黒变亮或由亮变黑,试设计这样的一个电路。
〔解题根本步骤:状态设置、设计真值表、写主析取式、化简、绘制电路. 答案不唯一〕§1.7 推理理论(习题1.19(1))用直接证明法或归谬法证明下面的推理.前提:¬(p∧¬q),¬q∨r,¬r. 结论:¬p.证明:…(习题1.19(3))用直附加前提法证明下面的推理.前提:P→q. 结论:P→(p∧q).证明:…〔例题1.28〕公安人员审查一件盗窃案,事实如下:(1)或王盗窃了录音机;(2)假如盗窃了录音机,如此作案时间不能发生在午夜前;(3)假如王的证词正确,如此午夜时屋里灯光未灭;(4)假如王的证词不正确,如此作案时间发生在午夜前;(5)午夜时屋里灯光灭了.试问盗窃录音机的是还是王,并证明你的结论。
参考答案:王盗窃了录音机.设p:盗窃了录音机;q:王盗窃了录音机;r:作案时间发生在午夜前;s:王的证词正确;t:午夜时屋里灯光灭了.前提:p∨q,p→¬r,s→t,¬s→r,¬t. 结论:q.证明:…CH02复习题§2.1例2.1〔3〕1 将命题“假如一的成绩比王二高,王二的成绩比吴三高,那么一的成绩比吴三高〞用0元谓词符号化。
解:设H(x,y):x的成绩比y高,a:一,b:王二,c: 吴三如此命题可符号化为H(a,b)∧H(b,c) H(a,c)§2.1例2.4〔4〕2 在一阶逻辑中将命题“素数不全是奇数〞符号化。
解:设F(x):x是素数,G(x):x是奇数如此命题可符号化为x(F(x)∧G(x))或x(F(x)G(x))§3 〔每空1分,共4分〕给定解释I,对一阶逻辑合式公式中每个出现的指定中的一个元素,称作在下的赋值。
〔自由个体变项个体域解释I〕§4 下面的一阶逻辑合式公式不是闭式。
(D 有自由出现)A x(F(x)G(X))B y(F(x,y)G(x))C xF(x)yG(y)D xF(x,y)yG(y)§5 下面各种表示,不正确。
(C 例2.8〔5〕) 也可改造成正误判断题A 在给定的解释和赋值下,任何一阶逻辑合式公式都是命题√P45-B 闭公式的真值与赋值无关,只需要给定解释C 非闭式的公式的真值只与赋值有关D 可满足式可能是逻辑有效式§6 在四个合式公式∀x∃y(F(x)→(G(y)∧H(x,y))) 、∀x(F(x)→∃y(G(y)∧H(x,y)))、∀x⌝(F(x)∧G(x))、⌝∃x(F(x)∧G(x)) 中共有个是前束式。
〔参考答案:A〕A 2B 3C 1D 0〔*参考答案:B〕7 F(x)=x(M(x)F(x)),G1(x)=x(M(x) F(x)),G2(x)=x(M(x)F(x)),G3(x)=x(M(x)F(x)),如此在G1(x)、G2(x)和G3(x)中,有个是F(x)的前束式。
A 0B 3C 2D 1例2.11〔3〕8 求公式xF(x)G(x) 的前束式。
解:xF(x)G(x)xF(x)xG(x) (蕴涵等值式)xF(x)xG(x) (量词否认等值式) xF(x)G(x) ) (量词分配等值式) 解法2:xF(x)G(x) xF(x)yG(y) (换名规如此)x(F(x)yG(y)) (量词扩TH2.2(2)③) xyF(x)G(y) ) (量词扩TH2.2(2)④)解法3:xF(x,)G(x)F(y)G(x) )§设个体域D={a,b},消去公式x(F(x)∧yG(y))中的量词。
离散CH03复习题判断〔1分/每一小题〕假如集合A={1,{1,2},3},如此2A 〔×〕假如集合B={2,{a,b}},如此{a,b}B 〔×〕单项选择〔2分/每一小题〕下面的集合算式不正确。
〔∵A=∴C〕A A-(B∪C)=A-B)∪(A-C)B A-B=A∩~BC A=AD A BA-B=B={ {a,b},c },如此|P(A)|=.〔∵P(A)= {,{c},{{a,b}},B},∴A〕A |{,{c},{{a,b}},B}|B 2C 3D 8填空〔2分/每一小题〕假如|P(A)| = 128,如此|A|=.(∵|P(A)|=27,∴7)设A={1,3,3},如此|A|=. ∵A={1,3},∴2)计算〔8分/每一小题〕某班有48个学生,第一次作业优秀7人,第二次作业优秀6人,两次作业都没得优秀的41人,求两次作业都得优秀的人数。
〔求解过程参见[例3.12],参考答案:6〕解:用A、B分别表示第一次和第二次作业优秀的人数集合,E为某班全体学生的集合如此:|E|=48,|A|=7,|B|=6,|~A∩~B|=41|~A∩~B| = |E|-(|A|+|B|)+|A∩B||A∩B| = 41-48+(7+6)= 6A={{a,b},c,d},B={c,d},计算A∩B、A∪B、A-B、AB。
〔P74-3.13(1)〕画图画〔A∩~B〕∪〔C-B〕的文氏图。
〔3.15〔3〕〕证明:〔A∩~B〕∪〔C-B〕=〔A∪C〕- B证:左式=〔A∩~B〕∪〔C∩~B 〕〔3.27 /差交运算转换〕= (A∪C)∩~B 〔3.8/分配律〕= (A∪C)-B 〔3.27 /差交运算转换〕离散CH04复习题判断〔1分/每一小题〕§1.A是任意集合,如此A×A的任何子集称作A上的二元关系。
〔√〕2. 假如集合B={2,{a,b}},如此{a,b}B 〔×〕单项选择〔2分/每一小题〕§3. A是任意集合,{<x,x>|xA}称作关系。
〔∵恒等关系蕴含其是A上的∴B〕A 空 B恒等 C 全域 D A上的4. 设A={a,b,c},R={<a,a>,<a,b >,< b,b>,<b,c>,<c,a>,<c,b>},如此是R 的关系矩阵。
〔参见P80-,参考答案:〔A〕A B C D设S={1,2,3,4},R是S上的关系,其关系矩阵是,R的关系图中有个环。
A 1B 3C 6D 7填空〔2分/每一小题〕§6. A、B是任意两个集合,假如|A|=m,|B|=n,如此|P(A×B)|=。
〔〕7.设A是任意集合,|A|=n,如此A上有个不同的二元关系。
(,|A×A|=n2)§8. R是集合A上的等价关系,如果有序对<a,b>R,如此记作。
〔a~b〕集合A上的偏序关系,如此可将此偏序关系简记作;有序对<x,y>,可记作。
〔ab〕计算〔8分/每一小题〕§10. 关系R={<2,{2}>,<{2},{2,{2}}>},求RR、R{2}、R[{2}]. (同例4.7 理解定义4.9)解:RR={<2,{2,{2}}>}R{2} = {<2,{2}>} 限制R[{2}] = ran〔R{2}〕= ran{<2,{2}>} = {{2}} 像集11.A={a,b,c,d},R1和R2是A上的关系,且R1={<a,a>,<a,b>,<b,d>},R2={<a,d>,<b,c>,<b,d>,<c,b>}。
求R2R1。
解:∵<a,a>R1<a,d>R2,∴<a,d>R2R1<a,b>R1<b,c>R2,∴<a,c>R2R1<a,b>R1<b,d>R2,∴<a,d>R2R1故R2R1={<a,d>,<a,c>}证明题综合:§1等值公式和等值运算+§3集合运算+§4关系性质的定义12. 设集合A上的两个关系R1和R2都是对称的,证明R1∩R2仍是对称的。
