线性系统的状态空间分析与综合
胡寿松《题海》第二版勘误与刷题指南

胡寿松《自动控制原理题海与考研指导》第二版勘误与刷题指南前言笔者本科电子信息工程,研究生跨考自动化,本科阶段没有学习《自动控制理论》,在备考期间没有做太多的题,仅仅做了专业课真题与胡寿松编篡的《自动控制原理题海与考研指导》第二版(以下简称题海)。
后来专业课考了145/150,不是说我专业课学的有多好,只是专业课出的确实十分简单,考上的同学专业课平均分也在130上下。
回顾备考点点滴滴,感觉受益《题海》良多。
但是《题海》许多题是重复思路,还有一些是答案有误。
为了让后来的学弟学妹们少走弯路,避免在题海中“溺亡”,笔者抽闲暇时光写一点经验与勘误。
如果能节省读者宝贵的刷题时间,在最短的时间内取得最好的复习效果,那我的初心就达到了。
奈何本人才疏学浅,失误在所难免,如有纰漏,烦请反馈给我。
邮箱:本勘误预计编篡七小节,分别是第一小节控制系统的数学模型、第二小节时域分析法、第三小节根轨迹法、第四小节频率响应法、第五小节线性系统的校正方法、第六小节非线性控制系统分析与第七小节线性系统的状态空间分析与综合。
针对《题海》,我没有写线性离散系统的分析与校正,因为上交考研大纲里面对此没有要求。
报考其它院校的同学还请自己刷离散部分了。
未来这七小节将陆续与大家见面,不定期更新。
感谢起点考研在备考过程中的指点与帮助!欢迎各位与著者交流分享学习经验。
目录第一节控制系统的数学模型............................................................................................ - 1 - 第二节时域分析法.............................................................................................................. - 4 - 第三节根轨迹法................................................................................................................... - 8 - 第四节频率响应法............................................................................................................ - 11 - 第五节线性系统的校正方法.......................................................................................... - 15 - 第六节非线性控制系统分析法 ..................................................................................... - 17 - 第七节线性系统的状态空间分析与综合................................................................... - 19 -第一节控制系统的数学模型2-1,无误 2-2,(1)(2)无误,(3)大家会求n=1,n=2就行了。
南京信息工程大学817自动控制原理2020年考研专业课初试大纲

南京信息工程大学硕士研究生招生入学考试考试大纲
考试科目代码:817
考试科目名称:自动控制原理
第一部分大纲内容
一、课程目标
本课程为控制系统提供了数学模型的建立、性能分析和系统设计的基本方法。
要求考生掌握自动控制系统的基本理论知识和基本分析计算方法,强调基础性和综合性。
注重测试考生对相关的基本概念、理论和分析方法的理解,以及运用基本概念、基本原理,灵活分析和解决实际问题的能力。
二、基本要求
考试内容包括经典控制理论和现代控制理论。
要求理解、掌握:控制系统传递函数和信号流图等数学模型的建立;系统稳定性、动态性能、稳态性能的时域分析;根轨迹法;频域法;系统串联校正的设计方法;线性离散系统的分析;系统状态空间建模及其求解;系统可控性和可观测性;线性定常系统状态反馈及观测器设计;李雅普诺夫稳定性理论。
三、课程内容与考核目标
(1)自动控制的一般概念
1.掌握基本控制方式:开环、闭环(反馈)控制;
2.熟悉自动控制的性能要求:稳、快、准;
3.掌握反馈控制原理与动态过程的概念,以及建立原理方块图的方法。
(2)控制系统的数学模型
1.掌握动态方程建立及线性化方法;
2.熟练掌握结构图的等效变换方法;
3.掌握梅逊公式及应用;
4.熟悉典型环节。
(3)线性系统的时域分析法。
南京信息工程大学2020考研大纲:817自动控制原理

南京信息工程大学2020考研大纲:817自动控制原理考研大纲频道为大家提供南京信息工程大学2019考研大纲:817自动控制原理,一起来了解一下吧!更多考研资讯请关注我们网站的更新!南京信息工程大学2019考研大纲:817自动控制原理考试科目代码:817考试科目名称:自动控制原理第一部分课程目标与基本要求一、课程目标本课程为控制系统提供了数学模型的建立、性能分析和系统设计的基本方法。
要求考生掌握自动控制系统的基本理论知识和基本分析计算方法,强调基础性和综合性。
注重测试考生对相关的基本概念、理论和分析方法的理解,以及运用基本概念、基本原理,灵活分析和解决实际问题的能力。
二、基本要求考试内容包括经典控制理论和现代控制理论。
要求理解、掌握:控制系统传递函数和信号流图等数学模型的建立;系统稳定性、动态性能、稳态性能的时域分析;根轨迹法;频域法;系统串联校正的设计方法;线性离散系统的分析;系统状态空间建模及其求解;系统可控性和可观测性;线性定常系统状态反馈及观测器设计;李雅普诺夫稳定性理论。
第二部分课程内容与考核目标(1)自动控制的一般概念1.掌握基本控制方式:开环、闭环(反馈)控制;2.明确自动控制的性能要求:稳、快、准;3.熟悉反馈控制原理与动态过程的概念,以及建立原理方块图的方法。
(2)数学模型1.掌握动态方程建立及线性化方法;2.熟练掌握结构图的等效变换方法;3.掌握梅逊公式及应用;4.熟悉典型环节。
(3)时域分析法1.掌握一、二阶系统的分析与计算(不要求记公式,典型响应以阶跃响应为主);2.熟练掌握系统稳定性的分析与计算:劳思、赫尔维茨判据;3.了解结构参数对系统响应影响的一般规律;稳态误差的计算及一般规律。
(4)根轨迹法1.熟悉根轨迹的概念与根轨迹方程;2.熟练掌握根轨迹的绘制法则;3.了解广义根轨迹的概念与绘制方法;4.掌握零、极点分布与阶跃响应性能的关系;5.理解主导极点与偶极子的概念。
(5)频率响应法1.熟悉线性系统的频率响应、典型环节的频率响应、系统开环的频率响应;2.熟练掌握频域性能指标、环节和系统频率响应曲线的绘制、Nyquist稳定判据和对数频率稳定判据的运用以及稳定裕度的计算;3.了解信号的频谱,闭环幅频与阶跃响应的关系,峰值及频宽的概念,开环频率响应与阶跃响应的关系;4.掌握三频段(低频段,中频段和高频段)的分析方法;5.明确最小相位和非最小相位的差别。
第五章线性定常系统的设计与综合-课件

(4)以便一个多输入—多输出系统实现“一个输入只控制一个输出”作 为
性能指标,相应的综合问题称为解耦控制问题。
优化型性能指标常取一个相对于状态 x 和控制 u 的二次型积分性能指标,
其形式为:
J(u()) (xTQxuTRu)dt 0
R正定对称;常阵
Q正定对称或半正 常定 阵对 (且 A,称 Q12)为能观测。
第五章 线性定常系统的设计与综合
二 输出反馈 输出反馈,就是将系统的输出量回馈到系统的 输入端,与参考输入一起,对受控对象进行控 制。在现代控制理论中,带输出反馈结构的控 制系统,根据反馈信号回馈点的位置不同,有 两种基本结构。 一种是反馈信号回馈至输入矩阵B的后端, 或者说,回馈点在状态微分处。图5-2为多输 入多输出系统输出反馈的这种结构型式。另一 种是反馈信号回馈至输入距阵B的前端,或者 说,回馈点在参考信号的入口处。图5-3为多 输入多输出系统输出反馈的这种结构型式。
(3)
其中:k 为 p×n常阵,状态反馈矩阵。
F为 p×q常阵,输出反馈矩阵。
v—参考输入向量。 2) 性能指标的类型
性能指标 非优化型性能指标:是一类不等式型的指标,即只要性能达
到或好于期望指标就算实现了综合目标。
优化型性能指标: 是一类极值型指标,综合的目的是要使
性能指标在所有可能值中取为极小(或
通过状态反馈构成闭环系统
x (ABK)xBu y(CDK)xDu
第五章 线性定常系统的设计与综合
一般D=0,可化简为
x (ABK)xBu yCx
闭环传递函数矩阵为
W k(s ) C (s IA B) 1 K B
状态反馈矩阵K的引入,并不增加系统的维 数,但可通过K的选择自由地改变闭环系统 的特征值,从而使系统获得所要求的性能。
812(自动控制原理)考试大纲

812(自动控制原理)考试大纲【一】差不多要求掌握操纵系统分析和综合差不多方法,要紧内容有传递函数和信号流图等数学模型的建立;系统稳定性、动态性能、稳态性能的时域分析;频域法和根轨迹法;系统串联校正的设计方法;线性离散系统的分析;系统状态空间建模及其求解;系统可控性和可观测性;线性定常系统状态反馈及观测器设计;李雅普诺夫稳定性理论。
【二】考试范围1、自动操纵的一般概念〔1〕自动操纵系统的定义、构成;〔2〕自动操纵系统的差不多操纵方式;自动操纵系统的分类;〔3〕对操纵系统的差不多要求;2、操纵系统的数学模型〔2〕传递函数的定义、性质及典型环节的传递函数;〔3〕信号流图的组成、建立及梅森增益公式;〔4〕闭环系统的传递函数:输入量及扰动量作用下的传递函数、误差传递函数。
3、线性系统的时域分析法〔1〕一阶系统动态性能;〔2〕二阶系统的动态性能:典型二阶系统的数学模型、欠阻尼阶跃响应、二阶系统的动态性能指标、二阶系统性能的改善;〔3〕操纵系统的稳定性分析及代数稳定判据;〔4〕操纵系统的稳态性能分析:稳态误差的定义、系统类型、稳态误差分析与静态误差系数。
4、线性系统的根轨迹法〔1〕根轨迹方程:幅值条件和相角条件;〔2〕180度根轨迹作图的一般规那么、典型的零、极点分布及其相应的根轨迹;〔4〕系统性能分析:稳定性分析、增加零、极点对根轨迹的妨碍、利用主导极点可能系统的性能指标;5、线性系统的频域分析法〔1〕频率特性;〔2〕典型环节与开环系统的频率特性;〔3〕奈奎斯特稳定判据及应用;〔4〕稳定裕度;6、线性系统的校正法〔1〕校正装置:超前、滞后网络的特性;〔2〕系统校正的频率响应法:超前、滞后校正设计;〔3〕PID操纵器:操纵法那么及对系统性能的妨碍。
7.线性离散系统的分析(1)信号采样和保持;(2)离散系统数学模型:差分方程和脉冲传递函数;(3)离散系统稳定性及稳定性判据;(4)离散系统稳态误差及动态性能分析;8.线性系统的状态空间分析与综合(1)线性系统的状态空间描述:建立、转换、标准型;线性系统的运动分析---状态方程的解;(2)线性系统的可控性和可观测性;(3)线性定常系统的线性变换;(4)线性定常系统的状态反馈极点配置和全维状态观测器设计;(5)李雅普诺夫稳定性分析。
《自动控制原理》第九章 线性系统的状态空间分析与综合

第九章 线性系统的状态空间分析与综合在第一章至第七章中,我们曾详细讲解了经典线性系统理论以及用其设计控制系统的方法。
可以看到,经典线性理论的数学基础是拉普拉斯变换和z 变换,系统的基本数学模型是线性定常高阶微分方程、线性常系数差分方程、传递函数和脉冲传递函数,主要的分析和综合方法是时域法、根轨迹法和频域法,分析的主要内容是系统运动的稳定性。
经典线性系统理论对于单输入-单输出线性定常系统的分析和综合是比较有效的,但其显著的缺点是只能揭示输入-输出间的外部特性,难以揭示系统内部的结构特性,也难以有效处理多输入-多输出系统。
在50年代蓬勃兴起的航天技术的推动下,在1960年前后开始了从经典控制理论到现代控制理论的过渡,其中一个重要标志就是卡尔曼系统地将状态空间概念引入到控制理论中来。
现代控制理论正是在引入状态和状态空间概念的基础上发展起来的。
在现代控制理论的发展中,线性系统理论首先得到研究和发展,已形成较为完整成熟的理论。
现代控制理论中的许多分支,如最优控制、最优估计与滤波、系统辨识、随机控制、自适应控制等,均以线性系统理论为基础;非线性系统理论、大系统理论等,也都不同程度地受到了线性系统理论的概念、方法和结果的影响和推动。
现代控制理论中的线性系统理论运用状态空间法描述输入-状态-输出诸变量间的因果关系,不但反映了系统的输入—输出外部特性,而且揭示了系统内部的结构特性,是一种既适用于单输入--单输出系统又适用于多输入—多输出系统,既可用于线性定常系统又可用于线性时变系统的有效分析和综合方法。
在线性系统理论中,根据所采用的数学工具及系统描述方法的不同,又出现了一些平行的分支,目前主要有线性系统的状态空间法、线性系统的几何理论、线性系统的代数理论、线性系统的多变量频域方法等。
由于状态空间法是线性系统理论中最重要和影响最广的分支,加之受篇幅限制,所以本章只介绍线性系统的状态空间法。
9-1 线性系统的状态空间描述1. 系统数学描述的两种基本类型这里所谓的系统是指由一些相互制约的部分构成的整体,它可能是一个由反馈闭合的整体,也可能是某一控制装置或受控对象。
线性系统的状态空间分析与综合
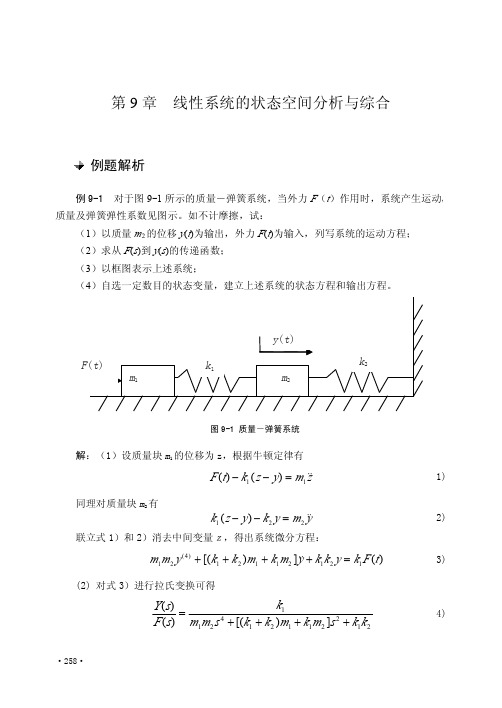
m1m2 y (4) + [(k1 + k 2 )m1 + k1m2 ]̇ẏ + k1k2 y = k1 F (t)
3)
(2) 对式 3)进行拉氏变换可得
Y(s) =
k1
4)
F (s) m1m2 s 4 + [(k1 + k2 )m1 + k1m2 ]s2 + k1k2
·258·
(3) 对式(1)进行拉氏变换可得
(1) 令
Z (s) Y (s) G(s) = •
2)
U (s) Z(s)
式中
Z(s) =
1
3)
U (s) s3 + 7s2 + 14s + 8
Y ( s ) = s 2 + 8 s + 15
4)
Z (s)
由式 3)
̇ż̇ + 7̇ż + 14ż + 8z = u
令
x1 = z ẋ1 = x2 = ż ẋ2 = x3 = ̇ż
⎡−1 0 0 ⎤ ⎡1⎤
故有
ẋ
=
⎢ ⎢
0
−2
0
⎥ ⎥
x
+
⎢⎢1⎥⎥u
⎢⎣ 0 0 − 4⎥⎦ ⎢⎣1⎥⎦
y
=
⎡8 ⎢⎣ 3
−3 2
−
1 6
⎤ ⎥⎦
x
·261·
两种形式的状态空间表达式所对应的状态图分别如图 9-4(a),(b)所示。
8
u
1 x3
1x
1
x1
1
y
s
s
2
s
-7
-
胡寿松《自动控制原理》笔记和课后习题(含考研真题)详解(线性系统的状态空间分析与综合)【圣才】

具有非正(负或零)实部,且具有零实部的特征值为 A 的最小多项式单根。
(2)系统的唯一平衡状态 xe=0 是渐近稳定的充分必要条件:A 的所有特征根均具有
3.线性定常连续系统状态方程的解 (1)齐次方程求解方法:幂级数法;拉普拉斯变换法。 (2)非齐次方程求解方法:积分法;拉普拉斯变换法。
4.传递函数矩阵 表达式:G(s)=C(sI-A)-1B+D
二、线性系统的可控性与可观测性 1.可控性 如果系统的每一个状态变量的运动都可由输入来影响和控制,而由任意的始点达到原点, 则该系统是完全可控系统,简称为系统可控。 (1)可控标准形
5 / 75
圣才电子书 十万种考研考证电子书、题库视频学习平台
的任意初始态 x0 出发的运动轨迹 x(t;x0,t0),在 t→∞都满足:||x(t;x0,t0)-xe||≤ε,
t≥t0,则称 xe 是李雅普诺夫意义下稳定的。
(3)渐近稳定
系统不仅满足李氏意义下的稳定,且
(2)可观测性判据
3 / 75
圣才电子书 十万种考研考证电子书、题库视频学习平台
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章线性系统的状态空间分析与综合
一、教学目的与要求:
通过本章内容的学习,使学生建立起状态变量和状态空间的概念,掌握线性定常系统状态空间模型的建立方法,状态空间表达式的线性变换,状态完全能控或状态完全能观测的定义,及其多种判据方法,状态转移矩阵的求法,传递函数矩阵与状态空间表达式的关系。
二、授课主要内容:
1.线性系统的状态空间描述
2.线性系统的可控性与可观测性
3.线性定常系统的状态反馈与状态观测器
(详细内容见讲稿)
三、重点、难点及对学生的要求(掌握、熟悉、了解、自学)
1.重点掌握线性定常系统状态空间模型的建立方法与其他数学描述(微分方程、
传递函数矩阵)之间的关系。
2.掌握采用状态空间表述的系统运动分析方法,状态转移矩阵的概念和求解。
3.掌握系统基本性质——能控性和能观测性的定义、有关判据及两种性质之间
的对偶性。
4.理解状态空间表达式在线性变换下的性质,对于完全能控或能观测系统,构
造能控、能观测标准形的线性变换方法,对于不完全能控或不完全能观测系统,基于能控性或能观测性的结构分解方法。
5.掌握单变量系统的状态反馈极点配置和全维状态观测器设计方法,理解分离
定理,带状态观测器的状态反馈控制系统的设计。
重点掌握线性系统的状态空间描述和求解,线性系统的可控性与可观测性及状态反馈与状态观测器。
四、主要外语词汇
线性系统 linear system
状态空间 state space
状态方程 state equation
状态向量 state vector
传递函数矩阵 translation function matrix
状态转换矩阵 state-transition matrix
可观测标准形 observational standard model
可控标准形 manipulative standard model
李亚普诺夫方程Lyaponov equation
状态观测器 state observation machine
对偶原理 principle of duality
五、辅助教学情况(见课件)
六、复习思考题
1.什么是系统的状态空间模型?状态空间模型中的状态变量、输入变量、输出变量各指什么?
2.通过机理分析法建立系统状态空间模型的主要步骤有哪些?
3.何为多变量系统?如何用传递矩阵来描述多变量系统的动态特性?
在多变量系统中,环节串联、并联、反馈连接时,如何求取总的传递矩阵?4.试简述数学模型各种表达式之间的对应关系。
5.用非奇异矩阵P对状态方程式进行线性状态变换后,与原状态方程式之间存在什么关系?
6.试简述系统能控性与能观性两个概念的含义及意义。
7.试述能控性和能观性定义。
8.试述系统能控性和能观性常用判据。
9.何谓对偶系统和对偶原理?
10.什么是状态方程的线性变换?
11.试述系统状态方程规范型变换的条件、特点及变换的基本方法。
12.试述状态能控性与能观性和系统传递函数(阵)的关系。
七、参考教材(资料)
1.《自动控制原理与系统》上、下册清华大学吴麒等国防工业出版社
参考该书第九章有关内容。
2. 《自动控制原理》 孙德宝 主编 化学工业出版社
参考该书第九章有关内容。
3.《现代控制理论》第2版 天津大学 刘豹主编 机械工业出版社
八、讲稿
第九章 状态空间分析与综合
9.1 引言
经典控制理论中常常采用系统关系来输入和输出之间的来描述一个控制系统。
这称之为控制系统的输入-输出描述。
微分方程和传递函数就是属于这种系统描述所采用的数学模型。
经典控制理论分析和设计控制系统所采用的方法是频率特性法和根轨迹法。
这两种方法用来分析和设计线性、定常单变量系统是很有效的。
但是,对于非线性系统、时变系统、多变量系统等,经典控制理论就显得无能为力了。
同时,随着生产过程自动化水平要求的提高,控制系统的任务越来越复杂,控制精度要求也越来越高,因此,建立在状态空间分析方法基础上的现代控制理论便迅速地发展起来。
9.2 状态空间和状态方程
9.2.1状态空间方法的几个基本概念
状态:所谓状态,是指系统过去、现在和将来的状况。
状态变量: 状态变量是指能确定系统运动状态的最少数目的一组变量。
一个用n 微分方程描述的系统就有n 个独立的变量,当这n 个独立变量的时间响应都求得时,系统的行为也就完全被确定。
因此,由n 微分方程描述的系统就有n 个状态变量。
状态变量具有非唯一性,因为不同的状态变量业能表达同一个系统的行为。
状态向量:若以n 个状态变量
向量x(t)的分量,则x(t)称为状态向量。
状态空间:以状态变量
构成的n 维空间,称为状态空间。
系统在任意时刻的状态向量x(t)在状态空间中是一个点。
系统随时间的变化过程,使x(t)在状态空间中描绘出一条轨迹。
状态空间表达式:将反映系统动态过程的n 微分方程或传递函数 ,转换成一阶微分方程组的形式,并利用矩阵和向量的数学工具,将一阶微分方程组用一个式子来表示,这就是状态方程。
将状态方程与描述系统状态变量与系统输出变量之间的关系的输出方程一起就构成了状态空间表达式。
下面就是状态空间表达式的标准描述
式中,分别为状态向量及其一阶导数, u(t),y(t)分别为系统的输入变量和输出变量, A, B, C 分别为具有一定维数的系统矩阵。
9.2.2 几个示例
【例9-1】RLC 电路的状态空间模型
12(),(),,()
n x t x t x t 12(),(),,()
n x t x t x t
设有如图9-1所示的RLC 电路,根据电工学的定理可以建立RLC电路的动态过程的微分方程为:
【例9-2】直流电动机速度控制系统
控制系统的一个常用的执行器是直流电动机。
它可以直接提供旋转运动,以及,通过飞轮、鼓和缆的耦合,可以提供变迁运动。
图9-2给出了一个电动机电枢绕组电路和连接着自由体的转子部分的示意图。
假定对上述对象,我们有以下物理参数:转子的转动惯量J= 0.01千克米2/秒2, 机械系统的阻尼比b=0.1牛米,电/力常数(K=Ke=Kt) = 0.01 牛米/安,电阻(R) = 1欧姆,电感L=0.5H,系统的输入为电压,输出轴的位置(θ),假定轴和转子是刚性的。
描述系统的数学模型-状态空间描述将包括以下两个部分:
(a) 输入对状态的作用关系式,它由状态方程来描述,是一组一阶微分方程式,或者是矩阵向量方程式。
9.3 线性系统状态空间表达式的建立
9.3.1高阶微分方程到状态空间描述
1. 输入信号不含导数项的n阶微分方程系统的状态空间描述
设单输入/单输出的控制系统的动态过程由下列n阶微分方程来描述
这里,x为n×1维列向量,A为n×n阶矩阵,B为n×1维列向量,C为1×n维列向量, u, y分别为系统的输入信号和输出信号。
式(9-14)即为控制系统的状态空间描述,式中矩阵A的形式为可控标准型。
图9-4给出了状态空间表达式的结构图。
式中,u,y分别为系统的输入和输出信号,试求系统的状态空间描述。
选择一组状态变量的原则是,应使导出的一阶微分方程组中,不能出现u(t)的导数项。
为此,可选取以下n个变量作为一组状态变量
式(9-22)即为含有输入信号导数项的控制系统的状态空间描述(包括状态方程和输出方程)
上式中,e(t)为E(s)的反拉氏变换,也即变量E(s)的时域表示。
将式(9-25)进行反拉氏变换,并将式(9-26)关系代入,则式(9-25)可改写成。
