大学物理C-练习四稳恒电流的磁场、电磁感应定律
电磁学内容总结_稳恒磁场与电磁感应_20091206

电磁学复习 —— 稳恒磁场与电磁感应1 磁感应强度、毕奥-萨伐尔定律、磁感应强度叠加原理 1) 磁感应强度的定义:0sin mF B q v α=—— 方向为运动电荷受到磁力为零的方向2) 磁场叠加原理:空间一点的磁感应强度服从叠加原理:i iB B =∑3) 磁通量:通过dS 的磁通量:m d B dS Φ=⋅02πθ≤<——m d Φ为正;2πθπ<≤ —— m d Φ为负通过任意曲面S 的磁通量:m SB dS Φ=⋅⎰通过一个闭合曲面S 的磁通量: m SB dS Φ=⋅⎰04) 毕奥-萨伐尔定律:02ˆ4Idl r dB r μπ⨯=—— 真空磁导率720201410/N A c μπε-==⨯ 一段电流在空间一点产生的磁感应强度:02ˆ4Idl rB dB rμπ⨯==⎰⎰运动电荷qv在真空中产生的磁感应强度:2ˆqv r B k r ⨯= —— 02ˆ4qv r B rμπ⨯= 2 稳恒磁场的高斯定理和安培环路定理1) 稳恒磁场的高斯定理:0SB dS ⋅≡⎰—— 无源场2) 安培环路定理在恒定电流产生的磁场中,磁感应强度沿任一闭合回路L 的线积分,等于闭合回路包围的所有电流代数和的0μ倍 —— 0int LLB dr I μ⋅=∑⎰3) 安培环路定理的应用应用安培环路定理求解磁感应强度的思路和方法电流分布的对称性:无限长均匀载流直导线、圆柱面、圆柱体;无限长载流直螺线管、环形载流螺线管;无限大载流平面磁场分布对称性:无限长均匀载流导线、圆柱面、圆柱体:磁力线为环绕中心轴线的同心圆,一个圆环上各点的磁感应强度大小相等,方向沿切线方向。
—— 无限长直螺线管:管内磁场沿轴线方向,同一条磁力线上各点磁感应强度大小相等。
—— 环形螺线管:管内磁场沿环形切线方向,同一个圆环上各点磁感应强度大小相等。
—— 各种电流分布产生的磁场,磁感应强度方向总是与电流方向满足右手螺旋关系。
选取积分回路:a )回路上各点磁感应强度大小为常数、方向沿回路各点切线方向;b )回路上部分磁感应强度积分为零,部分磁场为常数;c )规定闭合回路绕行的正方向; 4) 应用安培环路定理0int LLB dr I μ⋅=∑⎰进行计算 对于电流分布不对称的情况:由安培环路定理计算对称电流的磁场,再应用磁场叠加原理计算。
大学物理(4电磁感应定律)

第10章 电磁感应定律第一节 法拉第电磁感应定律1.电动势只有静电场不能维持稳恒电流。
(如电容器放电就是在静电场的作用下,电流由大到小到0的衰变过程,不能维持稳恒的电流。
) 要维持稳恒的电流,必须有非静电力作功,将其它形式的能量补充给电路,即电源。
在电源内部,非静电力使电荷从负极搬回到正极板。
电动势的定义:把单位正电荷从负极通过电源内部移到正极时,非静电力F k 所作的功。
把正电荷q 经电源内部由负极移到正极时,非静电力作的功为:k k A F dl +-=∙⎰电动势为:1k k A F dl q q ε+-==∙⎰例:5号电池的开路电压为1.5伏,充电电池的开路电压为1.2伏,这是由化学特性决定的。
在有电流输出时,电池两端的电压比开路电压低,原因是电源内部有电阻。
无内阻的电源称为“理想电源”2.法拉第定律精确的实验表明:导体回路中产生的感应电动势ξ的大小与穿过回路的磁通量的变化率d Φ/dt 成正比。
d dt εΦ=-实验1:磁铁插入线圈中,使线圈中的 磁通量发生变化,从而在线圈 中产生感应电动势。
实验2:内线圈通、断电的变化产生一个 变化的磁场,在外线圈中便产生 了感应电动势,其中没有任何移 动的部件,这样产生的电动势称 为感生电动势。
3.愣次定律(解决感应电动势的方向问题)闭合回路中,感应电流的方向总是使得它自身产生的磁通量反抗引起感应电流的磁通量的变化。
或者表述为:感应电流产生的磁场总是反抗磁通量的变化。
电动势方向0d dtΦ>d dtΦ<0d dt Φ> 0d dtΦ<0d dtΦ>0d dtΦ<0d dtΦ>0d dtΦ<。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
× × × × × × × × ×××××× × × × × × × × ×××××书中例题 10.2(p.443)一半径r =0.20m 的半园导线和直导线组成一回路,磁场垂直纸面向外,磁感应强度大小B =4t 2+2t+3,回路电阻R =2欧姆,其中接一电动势ε=2.0V 的理想电源(不计内阻)求:t =10s 时回路中的感应电动势的大小和方向及回路中的电流。
大学物理习题稳恒磁场

稳恒磁场一、选择题1. 一圆电流在其环绕的平面内各点的磁感应强度B 【 】 (A) 方向相同, 大小相等; (B) 方向不同,大小不等; (C) 方向相同, 大小不等; (D) 方向不同,大小相等。
2. 电流由长直导线流入一电阻均匀分布的金属矩形框架,再从长直导线流出,设图中321O ,O ,O 处的磁感应强度为B B B 123,,,则 【 】(A)B B B 123==; (B) 0B 0B B 321≠== ;(C) 0B ,0B ,0B 321=≠= ; (D) 0B ,0B ,0B 321≠≠=3. 所讨论的空间处在稳恒磁场中,对于安培环路定律的理解,正确的是 【 】(A) 若⎰=⋅L0l d B ,则必定L 上B 处处为零(B) 若⎰=⋅L0l d B, 则必定L 不包围电流(C) 若⎰=⋅L0l d B, 则L 所包围电流的代数和为零(D) 回路L 上各点的B 仅与所包围的电流有关。
4. 在匀强磁场中,有两个平面线圈,其面积21A 2A =, 通有电流21I 2I =, 它们所受的最大磁力矩之比M M 12/等于 【 】 (A) 1 (B) 2(C) 4(D) 1/45. 由N 匝细导线绕成的平面正三角形线圈,边长为a , 通有电流I , 置于均匀外磁场B中,当线圈平面的法向与外磁场同向时,该线圈所受的磁力矩M m 值为: 【 】(2)选择题(A) 2/IB Na 32,(B)4/IB Na 32, (C) 60sin IB Na 32,(D) 06. 一带电粒子以速度v 垂直射入匀强磁场 B 中,它的运动轨迹是半径为R 的圆, 若要半径变为2R ,磁场B 应变为: 【 】 B 22)D (B 21)C (B 2)B (B 2)A ( 7. 图中所示是从云室中拍摄的正电子和负电子的轨迹照片,均匀磁场垂直纸面向里,由两条轨迹可以判断【 】(A) a 是正电子,动能大; (B) a 是正电子, 动能小; (C) a 是负电子,动能大; (D) a 是负电子,动能小。
大学物理 恒定电流稳恒磁场知识点总结

大学物理 恒定电流稳恒磁场知识点总结1. 电流强度和电流密度 电流强度:单位时间内通过导体截面的电荷量 (电流强度是标量,可正可负);电流密度:电流密度是矢量,其方向决定于该点的场强E 的方向(正电荷流动的方向),其大小等于通过该点并垂直于电流的单位截面的电流强度dQ I dt =, dIj e dS= , S I j dS =⎰⎰ 2. 电流的连续性方程和恒定电流条件 电流的连续性方程:流出闭合曲面的电流等于单位时间闭合曲面内电量增量的负值(其实质是电荷守恒定律)dqj dS dt=-⎰⎰ , ( j tρ∂∇=-∂ ); 恒定电流条件: 0j dS =⎰⎰ , ( 0j ∇= ) 3. 欧姆定律及其微分形式: UI R=, j E σ=, ,焦耳定律及其微分形式: 2Q A I Rt == 2p E σ= 4. 电动势的定义:单位正电荷沿闭合电路运行一周非静电力所作的功AK dl q ε+-==⎰ , K dl ε=⎰5. 磁感应强度:是描述磁场的物理量,是矢量,其大小为0sin FB q v θ=,式中F 是运动电荷0q 所受洛伦兹力,其方向由 0F q v B =⨯决定 磁感应线:为了形象地表示磁场在空间的分布,引入一族曲线,曲线的切向表示磁场的方向,密度是磁感应强度的大小;磁通量:sB dS φ=⎰⎰ (可形象地看成是穿过曲面磁感应线的条数)6.毕奥一萨伐尔定律: 034Idl r dB r μπ⨯=34L Idl rB r μπ⨯=⎰7.磁场的高斯定理和安培环路定理磁场的高斯定理: 0SB dS =⎰⎰、 ( 0B ∇= ) (表明磁场是无源场)安培环路定理:0i LiB dl I μ=∑⎰、LSB dl j dS =⎰⎰⎰ 、(0B j μ∇⨯=)(安培环路定理表明磁场是有旋场)8.安培定律: dF Idl B =⨯ 、L F Idl B =⨯⎰磁场对载流线圈的作用: M m B =⨯ (m 是载流线圈的磁矩m IS =)9.洛伦兹力:运动电荷所受磁场的作用力称为洛伦兹力f qv B =⨯带电粒子在匀强磁场中的运动:运动电荷在匀强磁场中作螺旋运动,运动半径为mv R qB⊥=、周期为 2m T qB π= 、螺距为 2mv h v T qB π==霍尔效应 : 12HIBV V K h-= 式中H K 称为霍尔系数,可正可负,为正时表明正电荷导电,为负时表明负电荷导电 1H K nq=10.磁化强度 磁场强度 磁化电流 磁介质中的安培环路定理mM τ∑=∆ 、 LL M dl I =∑⎰,内、n i M e =⨯, 0BH M μ=- 、m M H χ= 、 00m r B H H μχμμμ==(1+)H=、 0i LiH dl I =∑⎰、LSH dl j dS =⎰⎰⎰。
4大学物理习题_稳恒磁场

稳恒磁场一、选择题1.一个半径为r 的半球面如右图放在均匀磁场中,通过半球面的磁通量为 (A )22r B π; (B )2r B π;(C )22cos r B πα; (D )2cos r B πα。
2.下列说法正确的是:(A )闭合回路上各点磁感应强度都为零时,回路内一定没有电流穿过; (B )闭合回路上各点磁感应强度都为零时,回路内穿过电流的代数和必为零; (C )磁感应强度沿闭合回路的积分为零时,回路上各点的磁感应强度必为零;(D )磁感应强度沿闭合回路的积分不为零时,回路上任意一点的磁感应强度都不可能为零。
3.如图,在一圆形电流I 所在的平面内,选取一个同心圆形闭合回路L ,则由安培环路定理可知(A )0=⋅⎰Ll d B,且环路上任意一点0=B 。
(B )0=⋅⎰Ll d B,且环路上任意一点0≠B 。
(C )0≠⋅⎰Ll d B ,且环路上任意一点0≠B 。
(D )0≠⋅⎰Ll d B,且环路上任意一点=B 常量。
4.图中有两根“无限长” 载流均为I 的直导线,有一回路L ,则正确的是(A )0=⋅⎰Ll d B,且环路上任意一点0=B ;(B )0=⋅⎰Ll d B,且环路上任意一点0≠B ;(C )0≠⋅⎰Ll d B,且环路上任意一点0≠B ;(D )0≠⋅⎰Ll d B,且环路上任意一点0=B 。
5.取一闭合积分回路L ,使三根载流导线穿过它所围成的面,现改变三根导线之间的相互间隔,但不越出积分回路,则:·LOI图(A )回路L 内的I ∑不变,L 上各点的B不变;(B )回路L 内的I ∑不变,L 上各点的B改变;(C )回路L 内的I ∑改变,L 上各点的B不变; (D )回路L 内的I ∑改变,L 上各点的B改变。
6.在球面上竖直和水平的两个载流圆线圈中,通有相等的电流I ,方向如图所示,则圆心处磁感应强度B的大小为(A )R I 0μ(B )R I20μ (C )RI 220μ(D )R I40μ7.一长直载流I 的导线,中部折成图示一个半径为R 的圆,则圆心的磁感应强度大小为 (A )R I 20μ;(B )RIπ20μ; (C )RIRIπ2200μμ+;(D )0。
大学物理练习题答案完美生活答案 06稳恒电流的磁场、电磁感应定律

dt
a
⎞ ⎟⎠
=
n
μ0 2π
l
I
⎛ ⎜⎝
1 R
−
1 R+
a
⎞ ⎟⎠
dR dt
=
μ0 2π
l
I
⎛ ⎜⎝
1 d
−
d
1 +
a
⎞ ⎟⎠
v
=
1×
2× 10−7×5 Nhomakorabea0×
0.4
×
2
×
⎛ ⎜⎝
1 0.20
−
0.20
1 +
0.20
⎞ ⎟⎠
成绩:
r d I
= 2 ×10−6(V ) ………4 分
方法二、相当于四段导体切割磁力线在瞬间,线圈产生的电动势等效于并接的两电动势。 距离长直导线为 r 处的磁感应强度为:
势。若若线圈保持不动,而长直导线中的电流变为交变电流 i = 10 sin (100π t ) A i=10,求线圈中的感应电动
势。(不计线圈的自感) 解:(1)方法(一)如图,距离长直导线为 r 处的磁感应强度为:
B = μ0i ,………2 分 2πr
选回路的绕行方向为顺时针方向,则通过窄条
6
专业班级: 面积 ds 的磁通量为:
d l
I
a
5
专业班级:
学号:
姓名:
在竖直方向的分量为 B .求ab两端间的电势差Ua −Ub .
解: Ob 间的动生电动势:
∫ ∫ ε1
=
4L 0
5
(υ
×
B)id l
=
4L 0
5
ω Bldl
=
1ωB( 4 25
大学物理练习册-稳恒磁场.
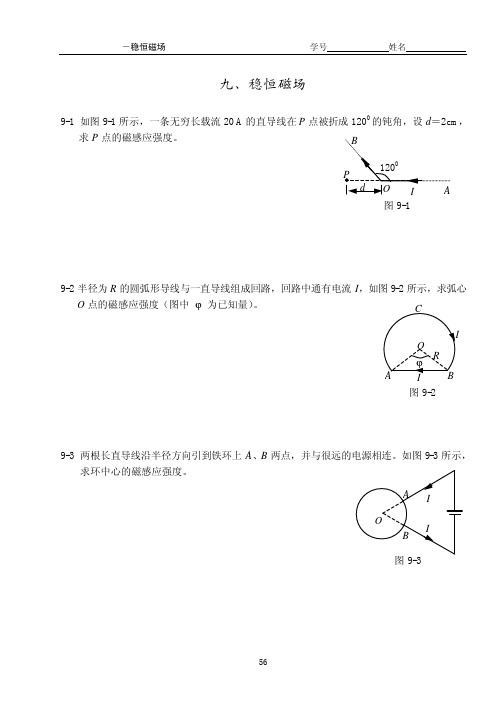
九、稳恒磁场磁感应强度9-1 如图9-1所示,一条无穷长载流20 A 的直导线在P 点被折成1200的钝角,设d =2cm ,求P 点的磁感应强度。
9-2半径为R 的圆弧形导线与一直导线组成回路,回路中通有电流I ,如图9-2所示,求弧心O 点的磁感应强度(图中 ϕ 为已知量)。
9-3 两根长直导线沿半径方向引到铁环上A 、B 两点,并与很远的电源相连。
如图9-3所示,求环中心的磁感应强度。
图9-1磁矩9-4一半径为R的薄圆盘,其中半径为r的阴影部分均匀带正电,面电荷密度为+s,其余部分均匀带负电,面电荷密度为-s(见图9-4)。
设此盘以角速度为ω绕其轴线匀速转动时,圆盘中心O处的磁感应强度为零,问R和r有什么关系?并求该系统的磁矩。
图9-49-5氢原子处在正常态(基态)时,它的电子可看作是在半径为a=0.53×10-8cm的轨道(称为玻尔轨道)上作匀速圆周运动,若电子在轨道中心处产生的磁感应强度大小为12.5T,求(1)电子运动的速度大小?(2)该系统的磁矩。
(电子的电荷电量e=1.6×10-19C)。
磁通量9-6已知一均匀磁场的磁感应强度B=2T,方向沿x轴正方向,如图9-6所示,已知ab=cd =40cm,bc=ad=ef=30cm,be=cf=30cm。
求:(1)通过图中abcd面的磁通量;(2)通过图中befc面的磁通量;(3)通过图中aefd面的磁通量。
图9-69-7两平行长直导线相距d=40cm,每根导线载有等量同向电流I,如图9-7所示。
求:(1)两导线所在平面内,与左导线相距x(x在两导线之间)的一点P处的磁感应强度。
(2)若I=20A,通过图中斜线所示面积的磁通量(r1=r3=10cm,l=25cm)。
图9-7安培环路定律9-8如图9-8所示的导体圆管,内、外半径分别为a和b,导体内载有电流I,设电流I均匀分布在导体圆管的横截面上,求:(1)磁感应强度的分布;(2)通过每米导体圆管S平面内(阴影部分)的磁感应通量。
大学物理练习题答案完美生活答案 06稳恒电流的磁场、电磁感应定律

ε2 =
∫ (υ × B)idl = ∫ ω Bldl = 2ω B( 5 L)
0 0
L5
1
1
2
=
1 ω BL2 50
a点电势高于O点.
∴ U a − U b = ε 2 − ε1 =
1 16 15 3 ω BL2 − ω BL2 = − ω BL2 = − ω BL2 50 50 50 10
6.如图所示,一无限长直导线通有电流 I=5.0A,一矩形单匝线圈与此长直导线共面。设矩形线圈以 V=2.0m/s 的速度垂直于长直导线向右运动。已知:l=0.40m, a=0.20m, d=0.20m,求矩形线圈中的感应电动 势。若若线圈保持不动,而长直导线中的电流变为交变电流 i = 10 sin ( 100π t ) A i=10,求线圈中的感应电动 势。 (不计线圈的自感) 解: (1)方法(一)如图,距离长直导线为 r 处的磁感应强度为:
ε1r1 ε2r2
R1 R2 R4
ε3r3 A
R3 B
1. 在真空中将一根细长导线弯成如图所示的形状(在同一平面内,
3
专业班级:
学号:
姓名:
成绩:
1 由实线表示), AB = EF = R ,大圆弧 BC 的半径为R,小圆弧 DE 的半径为 R ,求圆心O 处 2
的磁感强度 B 的大小和方向.
解:解:(1) AB , CD , EF 三条直线电流在O 点激发的磁场零;
2
专业班级: 正)为 (D) (A)
学号:
姓名:
成绩:
π r 2 B . . (B) 2π r 2 B .(C) −π r 2 B sin α . (D) −π r 2 B cos α
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练 习 四 稳恒电流的磁场、电磁感应定律
一、填空题
1. 如图所示,均匀磁场的磁感应强度为B =0.2T ,方向沿x 轴正方向,则通过
abod 面的磁通量为___0.024Wb ______,通过befo 面的磁通量为____0______,
通过aefd 面的磁通量为___0.024Wb ____。
2. 如图所示,两根无限长载流直导线相互平行,通过的电流分别为I 1和I 2。
则
=⋅⎰1
L l d B _____)(120I I -μ_______,=⋅⎰2
L l d B
_____)(120I I +μ_____。
3. 试写出下列两种情况的平面内的载流均匀导线在给定点P 处所产生的磁感强度的大小. (1) B = 08I R
μ ;
(2) B = 0 。
4. 感应电场是由 变化的磁场 产生的,它的电场线是 闭合曲线 。
5. 如图所示,一段长度为l 的直导线MN ,水平放置在载电流为I 的竖直长导线旁与竖直导线共面,并从静止由图示位置自由下落,则t 秒末导线两端的电势差
M N U U -________0ln
2Ig a l
t a
μπ+-
______________.
二、选择题
1. 一载有电流I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R=2r ),两螺线管
单位长度上的匝数相等。
两螺线管中的磁感应强度大小BR 和Br 应满足:( B) (A )BR=2Br (B )BR=Br (C )2BR=Br (D )BR=4Br
2. 磁场的高斯定理⎰⎰=⋅0S d B
说明了下面的哪些叙述是正确的? ( A )
a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;
b 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;
c 一根磁感应线可以终止在闭合曲面内;
301
d 一根磁感应线可以完全处于闭合曲面内。
(A )ad ; (B )ac ; (C )cd ; (D )ab 。
3. 如图所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量Φ和面上各点的磁感应强度B 将如何变化? ( D )
(A )Φ增大,B 也增大; (B )Φ不变,B 也不变; (C )Φ增大,B 不变; (D )Φ不变,B 增大
8. 如图所示,导体棒AB 在均匀磁场B 中 绕通过C 点的 垂直于棒长且沿磁场方向的轴OO '转动(角速度
ω与B 同方向),BC 的长度为棒长的1
3
,则 (A)
(A) A 点比B 点电势高. (B) A 点与B 点电势相等. (B) A 点比B 点电势低. (D) 有稳恒电流从A 点流向B 点
9. 在磁感强度为B 的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n 与B 的夹角为a ,则通过半球面S 的磁通量(取弯面向外为
正)为 (D)
(A) 2
r B π. . (B) 2
2r B π.(C) 2
sin r B πα-. (D) 2
cos r B πα-
10.图为四个带电粒子在O 点沿相同方向垂直于磁感线射入均匀磁场后的偏转轨迹的照片.磁场方向垂直纸面向外,轨迹所对应的四个粒子的质量相等,电荷大小也相等,则其中动能最大的带负电的粒子的轨迹是( C ) (A) Oa . (B) Ob .(C) Oc . (D) Od . 四、计算题
1. 在真空中将一根细长导线弯成如图所示的形状(在同一平面内,由实线表示),
AB EF R ==,大圆弧BC 的半径为R ,小圆弧DE 的半径为1
2
R ,求圆心O 处的磁感强度B 的
大小和方向.
解:解:(1) AB ,CD ,EF 三条直线电流在O 点激发的磁场零;
(2)
0BC B I R μ=
06DB B I R μ=
∴ 0006824O
I
I
I
B
R
R
R
μμμ=
-
=
方向为从O 点穿出纸面指向读者.
导线2中电流在P 点的磁感强度为02(1sin )4cos I
B a μθπθ
=
+
2B 方向垂直纸面向外.
P 点的总磁感强度为021(1sin cos )4cos I
B B B a μθθπθ
=-=
+-
B 的方向垂直纸面向外.
4. 如图所示,一无限长直导线通有电流I=
5.0A ,一矩形单匝线圈与此长直导线共面。
设矩形线圈以V=2.0m/s
的速度垂直于长直导线向右运动。
已知:l=0.40m, a=0.20m, d=0.20m 。
1.求矩形线圈中的感应电动势。
2.若若线圈保持不动,而长直导线中的电流变为交变电流
i t A 10sin 100
,求线圈中的感应电动势。
(不计
线圈的自感) 解:(1)
(2)如图,长直导线的磁感应强度为:
r
i
B πμ20=
,………2分
选回路的绕行方向为顺时针方向,则通过窄条 面积ds 的磁通量为:
02i
d Bds ldr r
μπΦ==………2分
通过矩形线圈的磁通量为
02d a
d
i
d ldr r
μπ+Φ=Φ=⎰⎰
0ln 2i d a l d
μπ+=
………3分
则:d n
dt
εΦ
=-0ln 2d l di n l d dt μπ+=-
70.050.20
10002100.05ln
10100cos1000.05
t ππ-+=-⨯⨯⨯⨯⨯⨯
0.21cos100()t V π=- ………4分
5.如图所示,一根长为L 的金属细杆ab 绕竖直轴O 1O 2以角速度ω在水平面内旋转.O 1O 2在离细杆a 端L /5 处.若已知地磁场在竖直方向的分量为B .求ab 两端间的电势差a b U U -. 解:Ob 间的动生电动势:
45
45
2210
1416
()()2550
L L B dl Bldl B L BL ευωωω=
⨯=
==
⎰
⎰
b 点电势高于O 点.
Oa 间的动生电动势:
5
2
220
111
()()2550
L L B dl Bldl B L BL ευωωω=
⨯=
==⎰
⎰ a 点电势高于O 点. ∴ 222221116153
50505010
a b U U BL BL BL BL εε
ωω
ωω-=-=
-=-=-。
