转子转动惯量计算
转动惯量
转动惯量一、基本概念惯量J 是一个常用的物理量,在负载被加速或减速的过程中中,是一个非常重要的参数。
转动惯量又可以称为惯性矩,它的的定义是:物体每一质点的质量m 与这一质点到旋转中心轴线的距离r 的二次方的乘积的总和,其数学表达式为:J =21m 2r 。
(1)在伺服控制系统中,大多数的传动机构具有圆柱状构件,因此,下面介绍几种圆柱状物体的转动惯量的计算。
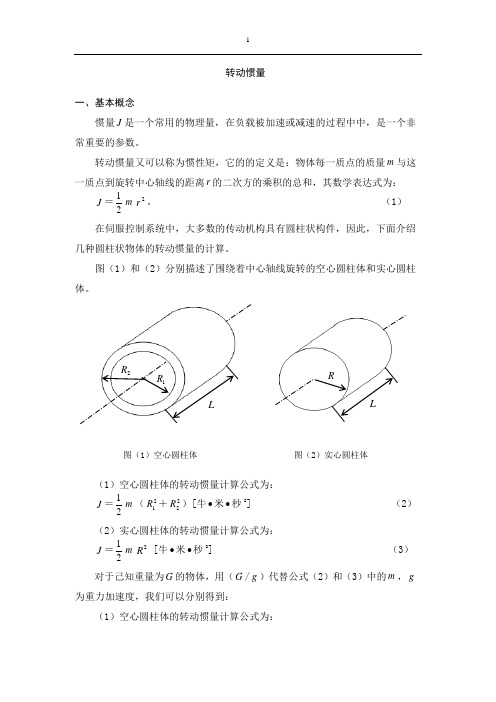
图(1)和(2)分别描述了围绕着中心轴线旋转的空心圆柱体和实心圆柱体。
图(1)空心圆柱体 图(2)实心圆柱体(1)空心圆柱体的转动惯量计算公式为:J =21m (21R +22R )[牛∙米∙秒2] (2)(2)实心圆柱体的转动惯量计算公式为:J =21m 2R [牛∙米∙秒2] (3)对于己知重量为G 的物体,用(G /g )代替公式(2)和(3)中的m ,g 为重力加速度,我们可以分别得到:(1)空心圆柱体的转动惯量计算公式为:J =gR R G 2)(2221+[牛∙米∙秒2] (4)(2)实心圆柱体的转动惯量计算公式为:J =gGR 22[牛∙米∙秒2] (5)如果重量不知道,但知道旋转物体的体积V 和密度γ,则可用(V γ/g )代替公/式(2)和(3)中的m ,我们可以得到:(1)空心圆柱体的转动惯量计算公式为:J =)(24142R R gL -γπ[牛∙米∙秒2] (6)(2)实心圆柱体的转动惯量计算公式为:J =42R gL γπ[牛∙米∙秒2] (7)二、计算 举例说明1.换向器的惯性矩K JK J =81.910)(32244-⨯-⨯K K KiK l D D γπ[克∙厘米∙秒2]。
换向器的几何尺寸: 换向器的外径K D =0.6[厘米]; 换向器的内径Ki D =0.38[厘米]; 换向器的轴向长度K l =0.5[厘米]。
在几何尺寸和材料已知的情况下,换向器的惯性矩K J 为:K J =81.910)(32244-⨯-⨯K K KiK l D D γπ= =81.9105.75.0)38.06.0(32244-⨯⨯⨯-⨯π=4.079×510- [克∙厘米∙秒2],式中,K γ是换向器材料的平均比重,取K γ≈7.5[克/厘米3]。
转子转动惯量

转子转动惯量
摘要:
1.引言
2.转子转动惯量的定义
3.转子转动惯量的计算方法
4.转子转动惯量的应用
5.结论
正文:
1.引言
在机械工程领域,转子转动惯量是一个重要的概念。
它直接影响到机械设备的运行稳定性、振动特性以及轴承的承载能力等。
因此,研究转子转动惯量对于提高机械设备的性能具有重要意义。
2.转子转动惯量的定义
转子转动惯量是指转子在旋转过程中,由于自身结构和质量分布的原因,产生的一种惯性力矩。
这种惯性力矩会使转子在旋转过程中产生阻力,从而影响转子的旋转速度和稳定性。
3.转子转动惯量的计算方法
计算转子转动惯量的方法通常有以下两种:
(1)理论计算方法:根据转子的形状、尺寸和质量分布,通过数学模型计算得出转子转动惯量。
(2)实验测量方法:通过实验装置,测量转子在旋转过程中的惯性力矩,从而得出转子转动惯量。
4.转子转动惯量的应用
转子转动惯量在机械工程中有广泛应用,例如:
(1)分析转子在旋转过程中的稳定性:通过计算转子转动惯量,可以判断转子在旋转过程中是否容易产生振动或失衡现象。
(2)选择轴承类型和尺寸:轴承的承载能力与转子转动惯量密切相关,因此,在设计轴承时需要考虑转子的转动惯量。
(3)优化转子结构:通过降低转子的转动惯量,可以提高机械设备的运行效率和稳定性。
5.结论
转子转动惯量是研究机械设备运行性能的重要参数,对于分析转子的稳定性、选择轴承类型和尺寸以及优化转子结构等方面具有重要应用价值。
电机转动惯量计算模型

电机转动惯量计算模型电机转动惯量是指电机在转动过程中克服转动惯性的能力大小,是电机转动惯性的度量。
它是电机工程中一个重要的参数,对电机的转速、起动、制动等性能有着重要的影响。
为了能够准确地计算电机的转动惯量,可以建立一个计算模型。
首先,我们需要了解电机的构造,电机主要由转子和定子组成。
转子是电机的运动部分,定子是电机的静止部分。
转子负责转动,而定子提供磁场。
电机的转动惯量主要由转子的结构和质量决定。
对于不同类型的电机,转动惯量的计算方法有所不同。
下面以直流电机为例进行分析。
直流电机转动惯量的计算模型可以分为两个部分:转子转动惯量和绕组转动惯量。
1.转子转动惯量的计算:转子转动惯量主要与转子的质量和形状有关。
我们可以将转子分割成若干个小块,然后对这些小块进行分别计算,最后将它们加总得到整个转子的转动惯量。
转子的转动惯量可以用以下公式计算:I_r=∑(m_i*r_i^2)其中,I_r为转子的转动惯量,m_i为各小块的质量,r_i为各小块到旋转轴的距离。
2.绕组转动惯量的计算:绕组转动惯量与绕组自身的结构和质量有关。
绕组一般由导线和绝缘材料组成,我们可以将绕组分割成若干个小块,然后对这些小块进行分别计算,最后将它们加总得到整个绕组的转动惯量。
绕组的转动惯量可以用以下公式计算:I_w=∑(m_i*r_i^2)其中,I_w为绕组的转动惯量,m_i为各小块的质量,r_i为各小块到旋转轴的距离。
绕组的质量可以通过绕组的几何参数和材料密度计算得到,而绕组各小块到旋转轴的距离可以通过几何关系得到。
最后,将转子的转动惯量和绕组的转动惯量加总,即可得到整个电机的转动惯量。
需要注意的是,以上的计算模型假设电机的各部分密度均匀且转动轴为转子的几何中心。
对于其他类型的电机,如异步电机和同步电机,转动惯量的计算方法也有所差异。
综上所述,电机转动惯量的计算模型包括转子转动惯量和绕组转动惯量的计算。
通过对电机的结构和质量进行分析和计算,可以准确地得到电机的转动惯量,为电机的设计和性能优化提供参考依据。
电机转动惯量计算公式

电机转动惯量计算公式
电机转动惯量是指电机在相同转速下所需的力矩大小,它是电机的一项重要参数。
电机转动惯量的大小取决于电机的物理结构,它可以通过一个特定的公式来计算。
电机转动惯量的计算公式如下:
J = (1/2)mvr2
其中,J是电机转动惯量,单位是千克·米2/秒2;m是转子的质量,单位是千克;v是转子的半径,单位是米;r是转速,单位是转/秒。
电机转动惯量的大小与转子的质量、半径和转速有关,当转子的质量、半径和转速增大时,电机转动惯量也会增大;当转子的质量、半径和转速减小时,电机转动惯量也会减小。
此外,电机转动惯量还受到电机物理结构的影响,比如电机的转子形状、磁芯材料以及绕组的结构都会影响电机转动惯量的大小。
电机转动惯量的计算公式可以帮助设计人员更好地了解电机的特性,帮助他们设计出更加合适的电机。
电机转动惯量的计算公式也可以帮助维修人员预测电机的表现,诊断电机的故障。
总的来说,电机转动惯量的计算公式是一个重要的工具,可以帮助设计人员更好地了解电机的特性,也可以帮助维修人员预测电机的
表现,诊断电机的故障。
转动惯量物理意义

转动惯量物理意义转动惯量是物体绕轴旋转时所具有的惯性量度,它反映了物体对于转动的抵抗能力。
在物理学中,转动惯量是描述物体转动运动特性的重要物理量之一。
本文将从物理意义、计算方法和应用方面介绍转动惯量的相关知识。
一、物理意义转动惯量的物理意义可以通过比较物体的转动运动和直线运动来理解。
在直线运动中,质点的惯性量度由质量所决定,而在转动运动中,物体的惯性量度由转动惯量所决定。
转动惯量越大,物体对于转动的抵抗能力越强,需要施加更大的力矩才能使其发生旋转;反之,转动惯量越小,物体对于转动的抵抗能力越弱,需要施加较小的力矩即可使其旋转。
二、计算方法转动惯量的计算方法取决于物体的形状和质量分布情况。
对于简单的几何形状,可以通过几何关系和积分计算来求解。
例如,对于长为L、质量均匀分布的细杆,其转动惯量可以通过以下公式计算:I = 1/3 * mL^2其中,m表示细杆的质量。
对于其他几何体,也可以通过类似的方法计算转动惯量。
对于复杂的物体,可以将其分解为一系列简单的几何体,然后求解每个几何体的转动惯量,并按照平行轴定理或垂直轴定理进行求和。
平行轴定理表示,如果已知一个物体关于通过其质心的轴的转动惯量,可以通过以下公式计算其关于平行于该轴的转动惯量:I = I_cm + md^2其中,I_cm表示物体关于质心轴的转动惯量,m表示物体的质量,d表示质心轴与平行轴的距离。
三、应用方面转动惯量在物理学和工程学中有着广泛的应用。
在物理学中,通过研究物体的转动惯量,可以深入理解刚体的转动运动规律,如角动量守恒定律和角动量的变化率等。
在工程学中,转动惯量的知识可以应用于机械设计、动力学分析等领域。
例如,在机械设计中,了解物体的转动惯量可以帮助工程师选择合适的电机或马达来驱动机械系统。
对于需要进行平衡设计的旋转部件,如飞轮、转子等,转动惯量的准确计算和控制可以确保系统的平衡性和稳定性。
转动惯量在物体的转动动能和转动动量等方面也有着重要的应用。
转子惯量和转动惯量的关系

转子惯量和转动惯量的关系
转子惯量和转动惯量是描述物体绕轴旋转的物理量,它们之间存在着密切的关系。
转子惯量通常指的是刚体绕着自身的轴旋转时所具有的惯性特性,而转动惯量则是一个更普遍的概念,用来描述物体在绕任意轴旋转时所具有的惯性。
转子惯量和转动惯量之间的关系可以通过以下公式来描述,转子惯量I关于某一轴的转动惯量I0等于转子惯量I关于通过物体质心的平行轴的转动惯量Ic,再加上物体质量m乘以距离d平方,即I0=Ic+md^2。
这个公式表明了转子惯量和转动惯量之间的关系,转子惯量关于某一轴的转动惯量等于转子惯量关于通过物体质心的平行轴的转动惯量再加上物体质量乘以距离平方。
这个公式可以帮助我们计算物体在绕任意轴旋转时的转动惯量,从而更好地理解物体的旋转运动特性。
此外,转子惯量和转动惯量的关系还可以通过物理实验和数学推导来加以证明。
通过实验测量不同形状和质量的物体在绕不同轴旋转时的转动惯量,可以发现它们之间确实存在着上述的关系。
同
时,利用数学方法可以推导出上述公式,进一步验证了转子惯量和
转动惯量之间的关系。
总之,转子惯量和转动惯量是描述物体旋转特性的重要物理量,它们之间通过特定的公式存在着密切的关系。
通过深入研究和理解
这一关系,可以帮助我们更好地理解物体的旋转运动规律,为相关
领域的应用和研究提供重要的理论基础。
转动惯量公式

nema标准中的计算是如下(转化公式):J=A×0.055613×(Pn^0.95)÷(n/1000)^2.4-0.004474×(Pn^1.5)÷(n/1000)^1.8A小于等于1800rpm时取24,A大于1800rpm时取27 Pn为功率(kw) n 为同步转速高压电动机在设计时,要求计算出转子的转动惯量。
下面对计算方法做一分析。
转动惯量是物体在转动时惯性的度量,它不仅与物体质量的大小有关,还与物体质量分体情况有关。
机械工程师手册给出了一些简单形状物体的转动惯量。
1、圆柱体沿轴线转动惯量:Kg•m2 (1)式中:M —圆柱体质量KgR —圆柱体外径半径 m2、空心圆柱体沿轴线转动惯量:Kg•m2 (2)式中: M —空心圆柱体质量KgR —空心圆柱体外半径 mr —空心圆柱体内半径m3、薄板沿对称线转动惯量:Kg•m2 (3)式中:M —薄板质量Kga —薄板垂直于轴线方向的宽度m物体的转动惯量除了用J表示外,在工程上有的用物体的重量G和物体的回转直径D的平方的乘积GD2来表示,也称为物体的飞轮力矩或惯量矩,单位N•m2或Kg f m2。
物体的飞轮力矩GD2和转动惯量J之间的关系,用下式表示:N•m2 (4)式中:g —重力加速度 g=9.81 m/s2将重力单位N化为习惯上的重力单位Kgf ,则(4)变为:Kg f m2 (5)由以上公式,可以对鼠笼型高压电机的转动惯量进行计算。
计算时,将高压电机转子分解为转子铁心(包括导条和端环)、幅铁、转轴三部分,分别算出各部分的Jn,各部分的转动惯量相加即得电机的转动惯量J。
如需要,按(5)式换算成飞轮力矩GD2。
一般产品样本中要求给定的是转动惯量J,兰州引进的电磁设计程序计算出的是飞轮力矩GD2。
计算程序如下:1、转子铁心的转动惯量,按空心圆柱公式(2)进行计算,考虑导条端环度大小的因素,以系数c进行修正。
转子转动惯量

转子的转动惯量(也被称为转动惯性或转动惯性矩)是描述物体对于转动的惯性特性的物理量。
它表示了物体围绕轴旋转时所表现的抵抗力。
转子的转动惯量取决于几个因素,包括转子的形状、质量分布以及围绕的轴线。
对于简单的刚体转子,转动惯量可以通过以下公式计算:
I = m * r^2
其中,I 是转动惯量,m 是转子的质量,r 是转子质量分布与旋转轴线之间的距离。
这个公式适用于旋转轴线通过转子的对称轴的情况。
对于其他情况下的复杂形状的转子,计算转动惯量需要使用积分等更复杂的数学方法。
请注意,转动惯量的单位通常是千克·米^2(kg·m^2)或克·厘米^2(g·cm^2),具体取决于所采用的单位制。
需要指出的是,转动惯量在实际应用中有着广泛的用途,包括机械工程、物理学、航空航天等领域。
在工程设计和运动学分析中,对于旋转系统的转动惯量的准确了解和计算非常重要。
