第10章 振动与波动(习题与答案)
振动与波动习题课修

A = 5 / cos α = 5 2 cm
2
πt 3π t= 0 t= 2 s (1) x = 5 2 × 10 cos( )( SI ) 4 4 3 π 2 (2) v = ω A sin = 5 2 × 10 sin( π ) 4 4 = 3 . 93 × 10 2 m / s
v A1
O X O
v A1
X O
A2
v A1
X
v A2
反相 同相
振动2比振动 超前 振动 比振动1超前 比振动
四、谐振动的合成 1。同方向、同频率的谐振动的合成: 。同方向、同频率的谐振动的合成:
A=
2 A12 + A2 + 2 A1 A2 cos( 2 1
A1 sin 1 + A2 sin 2 tg = A1 cos 1 + A2 cos 2
v0 tg = ω x0
两同频率的谐振动在任意时刻的相位差: 两同频率的谐振动在任意时刻的相位差:
= 2 1
振动2比振动1超前 > 0 LLLLL 落后 < 0 = = 2 kπ ( k = 0 ,1L ) 振动2和振动1同相 = ( 2 k + 1 )π ( k = 0 ,1L ) LLL反相
8. 一系统作简谐振动,周期为 ,以余弦函数 一系统作简谐振动,周期为T,
1 表达振动时,初相位为零。 表达振动时,初相位为零。在 0 ≤ t ≤ T范围 2 T/8或3T/8 时动能和势能相等 系统在t=_________时动能和势能相等。 时动能和势能相等。 内,系统在
解: x = Acosωt
x = 2cos(ωt + )
O t=0
5 Vm = ωA = 5 ω = 2 5 π x = 2cos( t )cm 2 2
《大学物理》 第二版 课后习题答案 第十章

习题精解10-1 在平面简谐波的波射线上,A,B,C,D 各点离波源的距离分别是3,,,424λλλλ。
设振源的振动方程为cos 2y A t πω⎛⎫=+ ⎪⎝⎭ ,振动周期为T.(1)这4点与振源的振动相位差各为多少?(2)这4点的初相位各为多少?(3)这4点开始运动的时刻比振源落后多少? 解 (1) 122,2,2xxπϕπϕππλλ∆∆∆==∆==3432,222x x πϕπϕππλλ∆∆∆==∆== (2)112233440,,2223,222πππϕϕϕϕππϕϕπϕϕπ=-∆==-∆=-=-∆=-=-∆=-(3) 1212343411,,,24223,,,242t T T t T T t T T t T Tϕϕππϕϕππ∆∆∆==∆==∆∆∆==∆==10-2 波源做谐振动,周期为0.01s ,振幅为21.010m -⨯,经平衡位置向y 轴正方向运动时,作为计时起点,设此振动以1400u m s -=∙的速度沿x 轴的正方向传播,试写出波动方程。
解 根据题意可知,波源振动的相位为32ϕπ= 2122200, 1.010,4000.01A m u m s T ππωπ--====⨯=∙ 波动方程231.010cos 2004002x y t m ππ-⎡⎤⎛⎫=⨯-+ ⎪⎢⎥⎝⎭⎣⎦10-3 一平面简谐波的波动方程为()0.05cos 410y x t m ππ=-,求(1)此波的频率、周期、波长、波速和振幅;(2)求x 轴上各质元振动的最大速度和最大加速度。
解 (1)比较系数法 将波动方程改写成0.05cos10 2.5x y t m π⎛⎫=-⎪⎝⎭与cos x y A t u ω⎛⎫=-⎪⎝⎭比较得1120.05;10;0.21015; 2.5;0.5A m T s v s u m s u T m Tπωππλ--=======∙=∙=(2)各质元的速度为()10.0510sin 410v x t m s πππ-=⨯-∙ 所以1max 0.0510 1.57()v m s π-=⨯=∙ 各质元的加速度为()220.05(10)cos 410a x t m s πππ-=-⨯-∙ 所以22max 0.05(10)49.3()a m s π-=⨯=∙10-4 设在某一时刻的横波波形曲线的一部分如图10.1所示。
10级大学物理复习题(第10章)

第10章 机械振动和波一、填空题易:1、质量为0.10kg 的物体,以振幅1cm 作简谐运动,其角频率为110s -,则物体的总能量为, 周期为 。
(4510J -⨯,0.628s )易:2、一平面简谐波的波动方程为y 0.01cos(20t 0.5x)ππ=-( SI 制),则它的振幅为 、角频率为 、周期为 、波速为 、波长为 。
(0.01m 、20π rad/s 、 0.1s 、 40m/s 、4m )易:3、一弹簧振子系统具有1.0J 的振动能量,0.10m 的振幅和1.0m/s 的最大速率,则弹簧的倔强系数为 ,振子的振动角频率为 。
(200N/m ,10rad/s )易:4、一横波的波动方程是y = 0.02cos2π(100t – 0.4X )( SI 制)则振幅是_________,波长是_ ,频率是 ,波的传播速度是 。
(0.02m ,2.5m ,100Hz ,250m.s -1)易:5、两个谐振动合成为一个简谐振动的条件是 。
(两个谐振动同方向、同频率)易:6、产生共振的条件是振动系统的固有频率与驱动力的频率 (填相同或不相同)。
(相同)易:7、干涉相长的条件是两列波的相位差为π的 (填奇数或偶数)倍。
(偶数)易:8、弹簧振子系统周期为T 。
现将弹簧截去一半,仍挂上原来的物体,作成一个新的弹簧振子,则其振动周期为 T 。
(T )易:9、作谐振动的小球,速度的最大值为,振幅为,则振动的周期为;加速度的最大值为。
(34π,2105.4-⨯)易:10、广播电台的发射频率为 。
则这种电磁波的波长为 。
(468.75m )易:11、已知平面简谐波的波动方程式为 则时,在X=0处相位为 ,在处相位为 。
(4.2s,4.199s)易:12、若弹簧振子作简谐振动的曲线如下图所示,则振幅;圆频率;初相。
(10m,1.2-s rad π,0)中:13、一简谐振动的运动方程为2x 0.03cos(10t )3ππ=+( SI 制),则频率ν为 、周期T 为 、振幅A 为 ,初相位ϕ为 。
第10章 波动(例题)

y(x,t) = 3×10−2 cos[4π(t − x / u) +π] −2 = 3×10 cos[4π(t − x / 20) +π]
-7-
第十章 波动
⑶C、D点的运动方程 点的运动方程
8m C
u
5m B A o 9m D
C点的运动方程 点的运动方程
x
y(xC ,t) = 3×10 cos4π (t − xC / u) = 3×10−2 cos4π(t − (−13)/20) −2 = 3×10 cos(4πt +13π / 5)
v v0
-17-
第十章 波动
v v0
解: 汽车接收声波 u + v车 ν汽收 = ν源 u 接收器接收反射波 u ν u ⋅ u + v车 ν = u + v车 ν ν器收 = 源 汽收 = u − v车 u − v车 u u − v车 源 解得 ν器收 −ν源 v车 = u = 110 −100 ×330 =15.7 m⋅ s-1 ν器收 +ν源 110 +100
-15-
第十章 波动
解: 观察者听到来自A的频率 ⑴观察者听到来自 的频率 u − v0 330 −30 ⋅ 500 = 454.5 Hz ν' = ν= u 330 观察者听到来自B的频率 的频率; ⑵观察者听到来自 的频率; u + v0 ν ′′ = ν = 330 + 30 ×500 = 461.5 Hz 330 + 60 u + vs 观察者听到的拍频. ⑶观察者听到的拍频 ∆ν =|ν ′ −ν ′′ |= 7 Hz
-19-
第十章 波动
解: 在观察时间飞机飞行的距离 AB = vst = h(cot + cotβ) α 飞机速度在AC、 方向的分量 飞机速度在 、BC方向的分量 vAC = vscosα vBC = vscosβ 飞机在A、 处观察者听到声音频率 飞机在 、C处观察者听到声音频率 u ν = u ν1 = ν0 0 u − vAC u − vscosα u ν2 = u ν0 = ν0 u + vBC u + vscosβ 解得 ν0 −ν2 ν1 −ν0 cosα = u = 0.275 cosβ = u = 0.413
第十章波动自测题

第十章波动自测题一、选择题1、关于“波长”的定义,下列说法正确的是< )<A)同一波线上振动位相相同的两质点间的距离<B)振动在一个周期内所传播的距离<C)同一波线上位相差为的两振动质点之间的距离<D)同一波线上两个波峰之间的距离2、下面说法正确的是< )<A)机械波是介质中的振动质点向远处传播形成的<B)只要有机械振动就一定会产生机械波<C)机械波的频率与波源的振动频率是一样的<D)机械波的速度与波源的振动速度是一样的3、对平面简谐波,下面几种说法中,错误的说法是:< )(A>波源的振动周期与波动的周期在数值上相同(B>波源的振动频率与波动的频率在数值上相同(C>波源振动的速度与波速相同(D>波源完成一次全振动,波向前传播一个波长4、下列说法正确的是< )<A)横波是沿水平方向振动的波,纵波是沿竖直方向振动的波;<B)机械波只能在弹性介质<媒质)中传播,而电磁波可以在真空中传播;<C)由于波速可表示为,则波源频率越高,波速越大;<D)波源振动的频率就是波的频率,波源振动的速度就是波的传播速度。
5、把一根长绳子拉成水平,用手握住其一端,维持拉力恒定,使绳端在垂直于绳子的方向上做简谐振动,则:< )b5E2RGbCAP<A)振动频率越高,波长越长<B)振动频率越低,波长越长<C)振动频率越高,波速越大<D)振动频率越低,波速越大6、当一列波由一种介质进入另一种介质中,它的波长、波速、频率三者的变化情况是< )<A)波长和频率会改变,波速不会变<B)波速和频率会改变,波长不会变<C)波速和波长会改变,频率不会变<D)波长、波速、频率都可能要改变7、横波以波速u沿x轴负方向传播,t时刻波形曲线如图,则该时刻< )<A)A点振动速度向上<B)B点静止不动<C)C点向下运动<D)D点振动速度向下8、以下说法错误的是< )(A> 波速与质点振动的速度是一回事,至少它们之间相互有联系(B> 波速只与介质有关,介质一定,波速一定,不随频率、波长而变,介质确定后,波速为常数(C> 质元的振动速度随时间作周期变化(D> 虽有关系式v = ν,但不能说频率增大,波速增大9、一横波沿绳子传播时的波动方程为y = 0.05 cos (10π t+4πx>(SI制>,则< )p1EanqFDPw<A)波长为0.5 m<B)波长为0.05 m<C)波速为25 m/s <D)波速为5 m/s10、一平面简谐波波动表达式为y=3cos(2πt-πx/2+π>,在x=4m位置处的质点在t=1s时刻振动速度为< )DXDiTa9E3d<A)6m/s <B)6πm/s<C)0m/s <D)-6m/s11、一简谐波的表达式为,式中的单位为m,的单位为s,则< )<A)波长 5m <B)波速为<C)周期为 <D)波沿χ轴正方向传播12、某波源作简谐振动,振动方程为m,已知波速为15m·s-1,则波的频率和波长分别为< )<A)25Hz,3.0×10-3m <B)25πHz,30m<C)25Hz,0.6m<D)25πHz,0.6m13、一平面简谐波表达式为y=-0.05sinπ(t-2x> (SI>,则该波的频率ν(Hz>,波速u(m/s>及波线上各点振动的振幅A(m>依次为< )RTCrpUDGiT(A> 1/2,1/2, -0.05(B> 1/2, 1 , -0.05(C> 2, 2, 0.05(D> 1/2, 1/2, 0.0514、一平面谐波沿x 轴正向传播,t=0时刻的波形如右上图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是:< )5PCzVD7HxA 15、一平面简谐波的波动方程为y = 0.1cos(3πt -πx+π> (SI>,t = 0时的波形曲线如图所示,则< )(A>O 点的振幅为-0.1m . (B> 波长为3m. (C> a 、b 两点间相位差为π/2. (D> 波速为9m/s.16、频率为100Hz ,传播速度为300m/s 的平面简谐波,波线上两点振动的相位差为π/3,则此两点相距< )xHAQX74J0X (A>2m(B> 2.19m(C> 0.5 m(D> 28.6 m17、如图所示为一平面简谐波在t=0时刻的波形图,该波的波速u=200m/s ,则P 处质点的振动曲线为下图中哪一图所画出的曲线?< )LDAYtRyKfE (A> (D> (C> (B>Zzz6ZB2Ltk 18、以下说法正确的是< )(A>在波传播的过程中,某质元的动能和势能相互转化,总能量保持不变(B>在波传播的过程中, 某质元任一时刻的动能与势能相等,且随时间作周期性的变化(C>在波传播的过程中, 某质元任一时刻的动能与势能相等,且不随时间发生变化(D>在波传播的过程中, 某质元任一时刻的动能与势能有可能相等,有可能不等,视时刻而定19、以下说法不正确的是< )(A> 从运动学角度看,振动是单个质点(在平衡位置的往复>运动,波是振动状态的传播,质点并不随波前进(B> 从动力学角度看振动是单个质点受到弹性回复力的作用而产生的,波是各质元受到邻近质元的作用而产生的dvzfvkwMI1(C> 从能量角度看,振动是单个质点的总能量不变,只是动能与势能的相互转化;波是能量的传递,各质元的总能量随时间作周期变化,而且动能与势能的变化同步rqyn14ZNXI (D> 从总体上看,振动即波动20.一平面简谐波在t =0时刻波形曲线如图所示,若波沿x 轴负方向传播,则下列对应质点振动曲线正确的是< )EmxvxOtOco(D>(C>(A>(B>二、填空题1、按照质点振动方向和波的传播方向的关系,机械波分为横波与两种基本形式。
第10章 波动习题解答

2
2
15 15 . 5
5 5 . 5
(2)距波源为16.0m和17.0m的两质点间相位差
16 ,17 (100 t 16 or : 2
2
) (100 t 17
2
)
x,
x 17 16 1 m ,
则( C )
(A)波长为100m; (C)周期为 解:y
1 3 s
(B)波速为10m/s; (D)波沿x轴正方向传播
x u )]
;
A cos[ ( t
6
T 2
y 0 . 05 cos[ 6 ( t
x 100
)]
1 3
s
u 100 m / s
uT 33 . 3 m
第十章
波动
习题解答
1
第十章 习题
10-1 图(a)表示t=0 时的简谐波的波形图,波沿x轴正
方向传播,图(b)为一质点的振动曲线. 则图(a)中所
表示的x=0处质点振动的初相位与图(b)所表示的振动
的初相位分别为(D )
y A cos(t ) v A sin( t )
(A)均为零
(D) 2 与
y 0
y
2
(B) 均为 2
u
x
y 0
(C) 均为
(E) 2 与
y
2
2
v 0 2
O
(a)
v 0 2
O
(b)
t
2
10-2 机械波的表达式为
基础物理学下册【韩可芳】第10章习题答案

第十章第十章第十章第十章 波动光学波动光学波动光学波动光学思考题思考题思考题思考题10-1 普通光源中原子发光有何特征?答答答:答:::因为普通光源是大量不同原子在不同时刻发的光,是自然光,因此不满足干涉条件,所以一 般普通光源观察不到干涉现象。
10-2 如何用实验检验一束光是线偏振光、部分偏振光还是自然光?答答答:答:::拿一块偏振片迎着这束光,转动偏振片,观察透射光。
(1)视场中光强有变化且有消光现象 的为线偏振光;(2)光强有变化但无消光现象的为部分偏振光;(3)光强无变化的为自然光。
10-3 自然光可以用两个独立的、相互垂直的、振幅相等的光振动表示。
那么线偏振光是否也可以用两个相互垂直的光振动表示?如果可以,则这两个相互垂直的光振动之间关系如 何?10-4 如何用实验测定不透明媒质的折射率?答答答:答:::光线入射到不透明的媒介上,改变入射角i ,并同时用偏振片测定反射光线的偏振化程度。
当反射光线为完全偏振光时,此时入射角i0 即为布儒斯特角,满足tan 可求得不透明介质的折射率n 。
10-5 如图(a)所示,一束自然光入射在方解石晶体的表面上,入射光线与光轴成一定角度;问将有几条光线从方解石透射 出来?如果把方解石切割成等厚的A 、B 两块,并平行地移 开很短一段距离,如图(b)所示,此时光线通过这两块方解石后有多少条光线射出来?如果把B 块沿沿沿沿光线转过一个角度, 此时将有几条光线从B 块射出来?为什么?i 0n ,测得 i0 即考思考思考思考题题题题10-5图图图图10-6 从普通光源获得两束相干光的一般方法是什么?在光的干涉中决定相遇点产生明纹或暗纹的因素是什么?答答答:答:::分波阵面法和分振幅法。
波源的相位差和波源到相遇点的光程差决定相遇点产生明纹或暗纹。
10-7 如图所示,设光线a 、b 从周相相同的A 、B 点传至P 点,试讨论:(1)在图中的三种情况下,光线a 、b 在相遇处P 是 否存在光程差?为什么?(2)若a 、b 为相干光,那么在相遇处的干涉情况怎 样?考题思考题思考题思考题 10-7 图图图图10-8 在杨氏双缝实验中,当作如下调节时,屏幕上的干涉条纹将如何变化?(要说明理由)(1)使两缝之间的距离逐渐减小;(2)保持双缝的间距不变,使双缝与屏幕的距离逐渐减小;(3)如图所示,把双缝中的一条狭缝遮住,并在两缝的垂直平分线上放置一块平面反射镜。
大学物理第10章 习题
r1
第十章 波动
16
物理学
第五版
第十章 习题
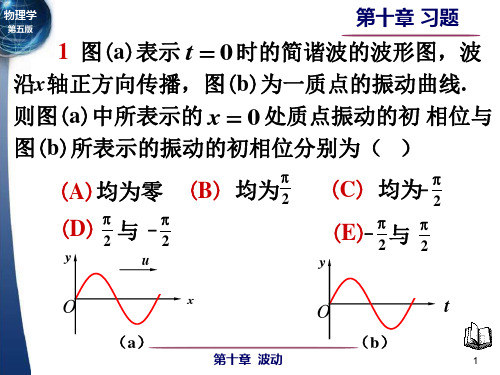
17 如图所示, 0 处有一运动方程为 x y A cos t 的平面波波源,产生的波沿x轴正、 负方向传播MN为波密介质的反射面,距波源 3λ / 4.求:(1)波源所发射的波沿波源O左右 传播的波动方程;(2)在MN处反射波的波动 方程;(3)在O~MN区域内形成的驻波方程, 以及波节和波腹的位置;(4)区域内合成波 M 的波动方程.
3 kg m ,求(1)该波的能流密度;(2)
1min内垂直通过4.0×10-4m2的总能量.
第十章 波动
13
物理学
第五版
第十章 习题
14 如图所示,两相干波源分别在P,Q 两点,它们发出频率为ν ,波长为 λ ,初 相相同的两列相干波,设PQ=3λ / 2 , R 为PQ连线上的一点.求:(1)自P、Q发 出的两列波在R处的相位差;(2)两波 在R处干涉时的合振幅.
3 一横波在沿绳子传播时的波动方程 为 y 0.20 cos 2.50t x) 式中y和x的单位 , ( 为 m , t的单位为s.(1) 求波的振幅、波速、 频率及波长;(2)求绳上的质点振动时的最 大速度;(3)分别画出t 1s 和 t 2s 时的波 形,并指出波峰和波谷.画出 x 1.0m 处质点的 振动曲线并讨论其与波形图的不同.
第十章 习题
5 已知一波动方程为 y 0.05 sin( 10t 2 x) 式中y的单位为 m ,t的单位为s. (1)求波长、频 率、波速和周期; (2)说明 x 0 时方程的意义, 并 作图表示.
第十章 波动
5
物理学
第五版
第十章 习题
6 有一平面简谐波在空间传播. 已知在波 线上某点B的运动规律为y A cos(t ) ,就 图(a)(b)(c)给出的三种坐标取法,分 别列出波动方程.并用这三个方程来描述与B相 距为b 的P点的运动规律.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第10章 振动与波动
一. 基本要求
1. 掌握简谐振动的基本特征,能建立弹簧振子、单摆作谐振动的微分方程。
2. 掌握振幅、周期、频率、相位等概念的物理意义。
3. 能根据初始条件写出一维谐振动的运动学方程,并能理解其物理意义。
4. 掌握描述谐振动的旋转矢量法,并用以分析和讨论有关的问题。
5. 理解同方向、同频率谐振动的合成规律以及合振幅最大和最小的条件。
6. 理解机械波产生的条件。
7. 掌握描述简谐波的各物理量的物理意义及其相互关系。
8. 了解波的能量传播特征及能流、能流密度等概念。
9. 理解惠更斯原理和波的叠加原理。
掌握波的相干条件。
能用相位差或波程差概念来分析和确定相干波叠加后振幅加强或减弱的条件。
10. 理解驻波形成的条件,了解驻波和行波的区别,了解半波损失。
二. 内容提要
1. 简谐振动的动力学特征 作谐振动的物体所受到的力为线性回复力,即
kx F -=
取系统的平衡位置为坐标原点,则简谐振动的动力学方程(即微分方程)为
x t
x 222d d ω-= 2. 简谐振动的运动学特征 作谐振动的物体的位置坐标x 与时间t 成余弦(或正弦)函数关系,即
)cos(ϕ+ω=t A x
由它可导出物体的振动速度 )sin(ϕ+ωω-=t A v
物体的振动加速度 )cos(ϕ+ωω-=t A a 2
3. 振幅A 作谐振动的物体的最大位置坐标的绝对值,振幅的大小由初始条件确定,即
2v ω+=2020x A
4. 周期与频率 作谐振动的物体完成一次全振动所需的时间T 称为周期,单位时间内完成的振动次数γ称为频率。
周期与频率互为倒数,即
ν=1T 或 T
1=ν 5. 角频率(也称圆频率)ω 作谐振动的物体在2π秒内完成振动的次数,它与周期、频率的关系为 ω
π=2T 或 πν=ω2
6. 相位和初相 谐振动方程中(ϕ+ωt )项称为相位,它决定着作谐振动的物体的状态。
t=0时的相位称为初相,它由谐振动的初始条件决定,即
00
x v ω-=ϕtan
应该注意,由此式算得的ϕ在0~2π范围内有两个可能取值,须根据t=0时刻的速度方向进行合理取舍。
7. 旋转矢量法 作逆时针匀速率转动的矢量,其长度等于谐振动的振幅A ,其角速度等于谐振动的角频率ω,且t=0时,它与x 轴的夹角为谐振动的初相ϕ,t=t 时刻它与x
轴的夹角为谐振动的相位ϕω+t 。
旋转矢量A ϖ的末端在x 轴上的投影点的运动代表着质
点的谐振动。
8. 简谐振动的能量 作谐振动的系统具有动能和势能,其
动能 )(sin ϕ+ωω==
t A m m E k 22222121v 势能 )(cos ϕ+ω==t kA kx E p 2222
121 机械能 22
1kA E E E p k =+= 9. 两个具有同方向、同频率的简谐振动的合成 其结果仍为一同频率的简谐振动,合振动的振幅
)cos(122122212ϕ-ϕ++=A A A A A
初相 22112
211ϕ+ϕϕ+ϕ=ϕcos cos sin sin tan A A A A
(1)当两个简谐振动的相差),,,( Λ210212±±=π=ϕ-ϕk k 时,合振动振幅最大,为21A A +,合振动的初相为1ϕ或2ϕ。
(2)当两个简谐振动的相差),,,( )(Λ2101212±±=π+=ϕ-ϕk k 时,合振动的振幅最小,为21A A -,合振动的初相与振幅大的相同。
10. 机械波产生的条件 机械波的产生必须同时具备两个条件:第一,要有作机械振动的物体——波源;第二,要有能够传播机械波的载体——弹性媒质。
11. 波长λ 在同一波线上振动状态完全相同的两相邻质点间的距离(一个完整波的长度),它是波的空间周期性的反映。
12. 周期与频率 波前进一个波长的距离所需的时间,它反映了波的时间周期性。
周
期的倒数称为频率,波源的振动频率也就是波的频率。
13. 波速u 单位时间里振动状态(或波形)在媒质中传播的距离,它与波源的振动速度是两个不同的概念。
波速u 、波长λ、周期T (频率ν)之间的关系为 uT =λ
14. 平面简谐波的波动方程 如果平面波沿x 轴正向传播,则其波动方程为
])(2 cos[ ])(2 cos[ ])([ cos 000ϕ+λ
-π=ϕ+λ-νπ=ϕ+-ω=x T t A x t A u x t A y 若波沿x 轴的负向传播,则其波动方程为
])(2 cos[ ])(2 cos[ ])([ cos 000ϕ+λ
+π=ϕ+λ+νπ=ϕ++ω=x T t A x t A u x t A y 其中0ϕ为坐标原点的初相。
15. 波的能量 波动中的动能和势能之和,其特点是同体积元中的动能和势能相等:
(1)在平衡位置处,动能最大,势能也最大;
(2)在最大位移处,动能最小(为零),势能也最小(为零);
(3)当媒质质元从最大位移处回到平衡位置的过程中:它从相邻的一段媒质质元获得能量,其能量逐渐增加。
(4) 当媒质质元从平衡位置运动到最大位移处的过程中:它把自己的能量传给相邻的一段质元,其能量逐渐减小。
16. 波的干涉 满足相干条件(同频率、同振动方向且相位差恒定)的两列波的叠加,其规律是:
(1)若两列波的相位差),,,( Λ210221212±±=π=λ
-π-ϕ-ϕ=ϕ∆k k r r 则合成振动的振幅有极大值:21A A A +=,为干涉加强(相长干涉)。
(2)若两列波的相位差),,,( )(Λ2101221
212±±=π+=λ-π-ϕ-ϕ=ϕ∆k k r r 合成振动的振幅有极小值:21A A A -=,为干涉减弱,当A 1=A 2时,相消干涉。
17. 驻波 无波形和能量传播的波称为驻波,它由两列同振幅的相干波在同一直线上沿相反方向传播时叠加而成,是波的干涉中的一个特例。
其振幅随x 作周期变化,因而为分段的独立振动,有恒定的波腹和波节出现。
