平曲线要素计算公式(给学生用的)
平曲线要素计算公式
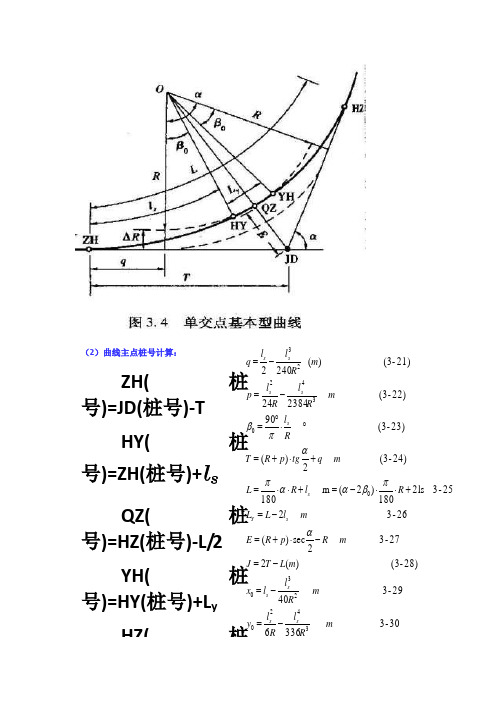
(2)曲线主点桩号计算:ZH(桩号)=JD(桩号)-T HY(桩号)=ZH(桩号)+ls QZ(桩号)=HZ(桩号)-L/2 YH(桩号)=HY(桩号)+L y HZ(桩30-3 336629-3 4028)-(3 )(227-3 2sec )(26-3 225-3 2ls 180)2(m 18024)-(3 2)(23)-(3 9022)-(3 23842421)-(3 )( 24023420230034223m Rl R l y m R l l x m L T J m R p R E m l L L R l R L m q tg p R T Rl m R l R l p m R l l q s s sss Y s s s s s s -=-=-=-⋅+=-=+⋅⋅-=+⋅⋅=+⋅+=︒⋅︒=-=-=απβααπαπβ第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:[例1]、某山岭区二级公路,变坡点桩号为K5+030.00,高程为427.68m,i1=+5%,i2=-4%,竖曲线半径R=2000m。
试计算竖曲线诸要素以及桩号为K5+000.00和K5+100.00处的设计高程。
解:1.计算竖曲线要素ω= |i2-i1|= |-0.04-0.05| =0.09,为凸型。
曲线长L=Rω=2000×0.09=180m切线长T=L/2=180/2=90m外距E=T2/2R=902/2×2000=2.03m2.计算设计高程竖曲线起点桩号=(K5+030.00)-90=K4+940.00竖曲线起点高程=427.68-90×0.05=423.18竖曲线终点桩号=(K5+030.00)+90=K5+120.00竖曲线终点高程=427.68-90×0.04=424.08桩号K5+000.00处:横距K5x 1=(K5+ 000.00)-(K4+940.00)=60m 竖距h 1=x 12/2R=602/2×2000=0.90m 切线高程=427.68-(90-60)×0.05=426.18m 423.18+60×0.05=426.18设计高程=426.18-0.90=425.28m 桩号K5+100.00处:横距x 2=(K5+120.00)-(K5+100.00)=20m 竖距h 2=x 22/2R=202/2×2000=0.1m切线高程=427.68-(90-20)×0.04=424.88m 设计高程=424.88-0.1=424.78m 横距x 2=(K5+100.00)-(K4+940.00)=160m 竖距h 2=x 22/2R=1602/2×2000=6.4m 切线高程=423.18+160×0.05=431.18m 设计高程=431.18-6.40=424.78m[例2]平原区某二级公路有一弯道,偏角α右=15°28′30″,半径R=600m ,缓和曲线长度Ls=70m , JD=K2+536.48。
平曲线要素计算公式

(2)曲线主点桩号计算:ZH(桩号)=JD(桩号)-T HY(桩号)=ZH(桩号)+ls QZ(桩号)=HZ(桩号)-L/2 YH(桩号)=HY(桩号)+L y HZ(桩30-3 336629-3 4028)-(3 )(227-3 2sec )(26-3 225-3 2ls 180)2(m 18024)-(3 2)(23)-(3 9022)-(3 23842421)-(3 )( 24023420230034223m Rl R l y m R l l x m L T J m R p R E m l L L R l R L m q tg p R T Rl m R l R l p m R l l q s s sss Y s s s s s s -=-=-=-⋅+=-=+⋅⋅-=+⋅⋅=+⋅+=︒⋅︒=-=-=απβααπαπβ第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:[例1]、某山岭区二级公路,变坡点桩号为K5+030.00,高程为427.68m,i1=+5%,i2=-4%,竖曲线半径R=2000m。
试计算竖曲线诸要素以及桩号为K5+000.00和K5+100.00处的设计高程。
解:1.计算竖曲线要素ω= |i2-i1|= |-0.04-0.05| =0.09,为凸型。
曲线长L=Rω=2000×0.09=180m切线长T=L/2=180/2=90m外距E=T2/2R=902/2×2000=2.03m2.计算设计高程竖曲线起点桩号=(K5+030.00)-90=K4+940.00竖曲线起点高程=427.68-90×0.05=423.18竖曲线终点桩号=(K5+030.00)+90=K5+120.00竖曲线终点高程=427.68-90×0.04=424.08桩号K5+000.00处:横距K5x 1=(K5+ 000.00)-(K4+940.00)=60m 竖距h 1=x 12/2R=602/2×2000=0.90m 切线高程=427.68-(90-60)×0.05=426.18m 423.18+60×0.05=426.18设计高程=426.18-0.90=425.28m 桩号K5+100.00处:横距x 2=(K5+120.00)-(K5+100.00)=20m 竖距h 2=x 22/2R=202/2×2000=0.1m切线高程=427.68-(90-20)×0.04=424.88m 设计高程=424.88-0.1=424.78m 横距x 2=(K5+100.00)-(K4+940.00)=160m 竖距h 2=x 22/2R=1602/2×2000=6.4m 切线高程=423.18+160×0.05=431.18m 设计高程=431.18-6.40=424.78m[例2]平原区某二级公路有一弯道,偏角α右=15°28′30″,半径R=600m ,缓和曲线长度Ls=70m , JD=K2+536.48。
平曲线计算

学习情景二Excel编写的计算过程
三、编写“支距法”放样的计算表格
根据上面介绍的专业知识,按如下步骤进行Excel计算的表格编写 1.编写计算表格 如图1一2一13所示 2.填写已知数据 编写结果如图1 -2一14所示 3.根据曲线计算方法,在表中计算过程中编写 具体计算结果如图1一2一15所示
(一)现代企业生产管理的地位 现代企业是一个有机的整体,现代企业生产管理就是一个
完 整 的 大 系 统 。 它 是 由 许 多 子系 统 有 序 构 成 的 , 生 产 管 理在现代企业管理系统中处于十分重要的地位,如图5 -1所示。
上一页 下一页 返回
任务一 生产管理认知
从图5-1可以看出生产管理和其他子系统的关系及生产 管理与经营决策的关系。
上一页 下一页 返回
学习情景一平曲线计算的专业知识
(2)圆曲线范围内
上一页 返回
学习情景二Excel编写的计算过程
一、编写平曲线要素的计算程序
根据上面介绍的专业知识,用如下流程进行Excel的计算。 1.编写计算表格 如图1一2一4所示 2.输入已知计算数据 如图1一2一5所示 3.计算 如图1一2一6所示 4.选定计算数据单元格 如图1一2一7所示
上一页 下一页 返回
任务一 生产管理认知
当前,激烈的市场竞争对企业的要求包括四个方面: 时间、 质 量 、 成 本 和 服 务 。 时 间 指满 足 顾 客 对 产 品 和 服 务 在 时 间方面的要求,即交货期要短而准; 质量指满足顾客对 产 品 和 服务 在 质 量 方 面 的 要 求 ; 成 本 指 满 足 顾 客 对 产 品 和 服 务 在 价 格 和 使 用 成 本 方 面 的 要 求 , 即 不 仅产 品 在 形 成过程中的成本要低,而且在使用过程中的成本也要低; 服 务 指 除 提 供 产 品 之 外 为满 足 顾 客 需 求 而 提 供 的 相 关 服 务,如产品的售前服务及售后服务等。
平曲线计算

表1一2一1已知工程数据
返回
图1一2一1带缓和曲线的曲线要索
返回
图1一2一2偏角法测设曲线
返回
图1
返回
图1 -2 -5输入已知数据
返回
图1一2一6结算结果显示
返回
图1一2一7选定单元格
返回
图1一2一8拉动结果
返回
图1一2一9计算显示
切线增长值
下一页 返回
学习情景一平曲线计算的专业知识
切线长 曲线长 或者 其中,圆曲线长 外距 切曲差
上一页 下一页 返回
学习情景一平曲线计算的专业知识
2.曲线主点里程计算 直缓点 缓圆点 曲中点 圆缓点 缓直点 交点
上一页 下一页 返回
学习情景一平曲线计算的专业知识
二、圆曲线带有缓和曲线的测设方法
下一页 返回
学习情景二Excel编写的计算过程
5.拉动单元格 将鼠标放在选定单元格的右下角,使其变成“+”号,然后向下
拉动,拉动过程中,单元格中会出现错误,可以不必理会。如图1一2 一8所示。 6.填写已知条件
填写已知条件JD桩号、半径R、缓和曲线长度LS ,曲线偏角PJ, 就可计算出相应的曲线要素和主点桩号,如图1 -2 -9所示
任务二平曲线计算
学习情景一平曲线计算的专业知识 学习情景二Excel编写的计算过程 实践教学情景Excel工程应用一
学习情景一平曲线计算的专业知识
一、曲线要素的计算
以单交点平曲线为例,如图1 -2一1所示,只设一个JD点的平 曲线成为单交点平曲线,主要计算要素已经给定,但是为方便进行平 曲线的计算,下面先进行复习。 1.曲线要素的计算 已知条件:JD桩号、半径R,偏角PJ、缓和曲线LS 求解:切线长T,曲线长L,外距E,切曲差D, ZH, HY, QZ, YH, HZ 计算公式如下: 内移值
公路基本型平曲线(回旋缓和曲线)要素及计算公式
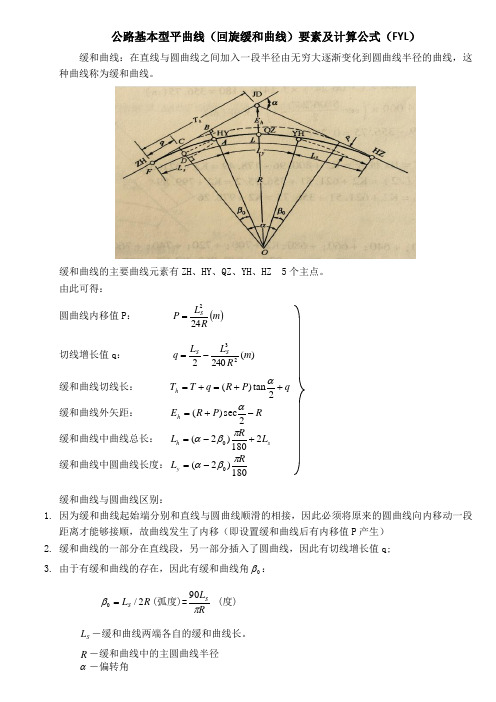
公路基本型平曲线(回旋缓和曲线)要素及计算公式(FYL )缓和曲线:在直线与圆曲线之间加入一段半径由无穷大逐渐变化到圆曲线半径的曲线,这种曲线称为缓和曲线。
缓和曲线的主要曲线元素有ZH 、HY 、QZ 、YH 、HZ 5个主点。
由此可得:圆曲线内移值P : ()m R L P S 242=切线增长值q : )(240223m R L L q S S -= 缓和曲线切线长: q P R q T T h ++=+=2tan)(α 缓和曲线外矢距: R P R E h -+=2sec )(α缓和曲线中曲线总长: s h L R L 2180)2(0+-=πβα 缓和曲线中圆曲线长度:180)2(0R L y πβα-=缓和曲线与圆曲线区别: 1. 因为缓和曲线起始端分别和直线与圆曲线顺滑的相接,因此必须将原来的圆曲线向内移动一段距离才能够接顺,故曲线发生了内移(即设置缓和曲线后有内移值P 产生)2. 缓和曲线的一部分在直线段,另一部分插入了圆曲线,因此有切线增长值q;3. 由于有缓和曲线的存在,因此有缓和曲线角0β:R L S 2/0=β(弧度)=RL S π90 (度) S L -缓和曲线两端各自的缓和曲线长。
R -缓和曲线中的主圆曲线半径α-偏转角缓和曲线主点桩号:ZH 桩号=JD 桩号-h THY 桩号=ZH 桩号+S LQZ 桩号=HY 桩号+2yLYH 桩号=QZ 桩号+2yLHZ 桩号=ZH 桩号+h L另外、QZ 桩号、YH 桩号、HZ 桩号还可以用以下方式推导:QZ 桩号=ZH 桩号+2hLYH 桩号=HZ 桩号-S LHZ 桩号=YH 桩号+S L切线支距法计算坐标:缓和曲线段内坐标计算如式: 22540SPp L R L L -=X sPRL L Y 63=进入净圆曲线段内坐标计算如式: ⎥⎦⎤•⎪⎪⎭⎫- ⎝⎛⎢⎣⎡+=R L L R q X s p π1802sin ⎭⎬⎫⎥⎦⎤•⎪⎪⎭⎫- ⎝⎛⎢⎣⎡-⎩⎨⎧+=R L L R P Y s p π1802cos 1 上述公式还可以简化为:αsin R q X +=()αcos 1-+=R P Y+-=R L L s p πα)180(0βR L S 2/0=β(弧度)=R L Sπ90 (度)。
平曲线计算公式

平曲线计算公式摘要:一、引言二、平曲线计算公式介绍1.圆曲线2.缓和曲线三、计算方法1.圆曲线计算方法2.缓和曲线计算方法四、实际应用1.在道路设计中的应用2.在铁路设计中的应用五、结论正文:一、引言平曲线计算公式是道路和铁路设计中非常重要的一个概念,它涉及到道路和铁路的曲率半径、超高缓和段长度等关键参数的计算。
本文将详细介绍平曲线计算公式及其在实际工程中的应用。
二、平曲线计算公式介绍平曲线分为圆曲线和缓和曲线两种,下面分别介绍这两种曲线的计算公式。
1.圆曲线圆曲线是最简单的平曲线形式,其计算公式如下:R = (V^2 / g) / (1 + (h / R)^2)其中,R 为曲率半径,V 为设计速度,g 为重力加速度,h 为超高缓和段长度。
2.缓和曲线缓和曲线是为了克服圆曲线在高速行驶时产生的离心力而设计的曲线形式。
缓和曲线的计算公式较为复杂,通常需要通过数值方法求解。
三、计算方法1.圆曲线计算方法根据圆曲线计算公式,可以求解出曲率半径R。
在实际应用中,需要根据设计速度V 和超高缓和段长度h 这两个已知条件,计算出合适的曲率半径R。
2.缓和曲线计算方法缓和曲线的计算方法通常采用数值方法,例如牛顿法、梯度下降法等。
在实际应用中,需要根据设计要求设定初始值,然后通过迭代计算,逐步逼近最优解。
四、实际应用1.在道路设计中的应用平曲线计算公式在道路设计中具有重要意义,它直接影响到道路的行驶安全性、舒适性和经济性。
正确使用平曲线计算公式,可以为道路设计提供科学依据,提高道路设计的质量。
2.在铁路设计中的应用与道路设计类似,平曲线计算公式在铁路设计中也具有重要意义。
在高速列车行驶过程中,平曲线的设置将直接影响到列车的运行安全、舒适性和能耗。
因此,在铁路设计中,需要根据列车设计速度和线路条件,合理设置平曲线,以满足列车运行要求。
五、结论平曲线计算公式是道路和铁路设计中的关键概念,掌握平曲线计算公式对于提高设计质量和保障工程安全具有重要意义。
平曲线竖曲线计算

平曲线、竖曲线计算一 平曲线计算1.1 导线点计算 设计线大致如下所示:根据地形图可以得出起点(A )、交点(B )、终点(C )的坐标,如下所示: A :(3850483.572,496529.666) B :(3850231.315,497311.415) C :(3850142.008,499016.194) 路线长度、方位角计算 (1)AB 段821.440AB D m ==497311.415496529.6667202'58"3850231.3153850483.572AB arctgβ-==-。
因为图在第二象限里,故180-7202'58"10753'02"AB θ==。
(2)BC 段1707.117BC D m ==499016.194497311.4158700'04"3850142.0083850231.315BC arctgβ-==-。
因为图在第二象限里,故1808700'04"9259'56"BC θ=-=。
(3)转角计算10753'02"9259'56"1453'06"α=-=。
(左)1.2平曲线参数计算已知1453'06"α=。
,1000R m =,120s L m =。
平曲线各参数计算如下:332212012059.993224022401000s s L L q m R =-=-=⨯242433'"'"'"'"1201200.6002423842410002384100012028.647928.6479326151000145306()(10000.600)59.993190.704223.142(2)2(145306232615)1000180180s s s o o s L L p mR R L R T R p tg q tg m L R L βαπαβ=-=-=⨯⨯==⨯==++=+⨯+==-+=-⨯⨯⨯。
平曲线计算公式

平曲线计算公式(原创版)目录1.引言2.平曲线计算公式的定义与分类3.平曲线计算公式的应用4.平曲线计算公式的优缺点5.结论正文1.引言平曲线是道路工程中常见的一种曲线形式,它是指在道路的纵断面上,道路中心线在水平方向上呈平滑变化的曲线。
平曲线的计算对于道路的设计与施工具有重要意义,而平曲线计算公式则是实现这一目标的关键工具。
本文将详细介绍平曲线计算公式的定义与分类、应用、优缺点等方面的内容。
2.平曲线计算公式的定义与分类平曲线计算公式是指在道路工程中,用来计算道路中心线在纵断面上呈平滑变化的曲线公式。
根据计算方法的不同,平曲线计算公式可以分为以下几类:(1)基于矢量的计算公式:这类公式主要利用矢量的运算来计算平曲线,如计算曲线的曲率、切线角等。
(2)基于参数的计算公式:这类公式主要通过参数方程来描述平曲线,如用弧长、半径等参数来表示曲线。
(3)基于几何图形的计算公式:这类公式主要通过几何图形的性质来计算平曲线,如通过椭圆、抛物线等几何图形来表示曲线。
3.平曲线计算公式的应用平曲线计算公式在道路工程中有广泛的应用,主要包括以下几个方面:(1)道路设计:通过计算平曲线,可以得到道路中心线在纵断面上的形状,从而满足道路的安全、舒适、经济等设计要求。
(2)道路施工:在道路施工过程中,需要根据平曲线计算公式来控制道路中心线的形状,以保证道路的施工质量。
(3)道路维护:在道路维护过程中,通过对平曲线的计算与分析,可以及时发现道路的不良状况,为道路的维护提供依据。
4.平曲线计算公式的优缺点平曲线计算公式具有以下优点:(1)计算简便:平曲线计算公式具有明确的计算步骤和简单的计算方法,便于工程技术人员掌握和使用。
(2)适用性强:平曲线计算公式适用于各种类型的道路,无论是直线、曲线还是复合曲线,都可以采用相应的公式进行计算。
然而,平曲线计算公式也存在一定的缺点:(1)计算精度受限:由于公式本身的局限性,平曲线计算公式的计算精度受到一定的限制,可能无法满足某些高精度计算的需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平曲线要素计算公式(给学生用的)
1 / 3
第三节 竖曲线
纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线采用
抛物线拟合。
一、竖曲线要素的计算公式
(2)曲线主点桩号计算:
ZH(桩号)=JD(桩号)-T
HY(桩号)=ZH(桩号)+l
s
QZ(桩号)=HZ(桩号)-L/2
YH(桩号)=HY(桩号)+Ly
HZ(桩号)=YH(桩号)+ls
JD(桩号)=QZ(桩号)+J/2
30-3 336629-3 4028)-(3 )(227-3 2sec)(26-3 225-3 2ls 180)2(m 18024)-(3 2)(23)-(3 9022)-(3 23842421)-(3 )( 240234202300034223mRlRlymRllxmLTJmRpREmlLLRlRLmqtgpRTRlmRlRlpmRllqsssssYssssss
平曲线要素计算公式(给学生用的)
2 / 3
相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1
ω为正时,是凹曲线;ω为负,是凸曲线。
2.竖曲线诸要素计算公式
竖曲线长度或竖曲线半径R: (前提:ω很小)
L=Rω
竖曲线切线长:T=L/2=Rω/2
竖曲线上任一点竖距h:
竖曲线外距:
[例1]、某山岭区二级公路,变坡点桩号为K5+030.00,标高为427.68m,变坡点桩号的地
面高程为450.65m,i1=+5%,i2=-4%,竖曲线半径R=2000m。试计算竖曲线诸要素以及桩
号为K5+000.00和K5+100.00处的设计高程,BPD的设计高程与施工高。
解:1.计算竖曲线要素
ω= |i2-i1|= |-0.04-0.05| =0.09,为凸型。
曲线长L=Rω=2000×0.09=180m切线长T=L/2=180/2=90m
外距E=T2/2R=902/2×2000=2.03m
2.计算设计高程
竖曲线起点桩号=(K5+030.00)-90=K4+940.00
竖曲线起点高程=427.68-90×0.05=423.18
竖曲线终点桩号=(K5+030.00)+90=K5+120.00
竖曲线终点高程=427.68-90×0.04=424.08
桩号K5+000.00处:
横距K5x1=(K5+ 000.00)-(K4+940.00)=60m
竖距h1=x12/2R=602/2×2000=0.90m
切线高程=427.68-(90-60)×0.05=426.18m
423.18+60×0.05=426.18
设计高程=426.18-0.90=425.28m
桩号K5+100.00处:
平曲线要素计算公式(给学生用的)
3 / 3
横距x2=(K5+120.00)-(K5+100.00)=20m
竖距h2=x22/2R=202/2×2000=0.1m
切线高程=427.68-(90-20)×0.04=424.88m
设计高程=424.88-0.1=424.78m
横距x2=(K5+100.00)-(K4+940.00)=160m
竖距h2=x22/2R=1602/2×2000=6.4m
切线高程=423.18+160×0.05=431.18m
设计高程=431.18-6.40=424.78m
BPD设计高程=427.68-E=425.65m
BPD施工高=设计高程-地面高程=425.65-450.65=-25m,应为挖方。
[例2]平原区某二级公路有一弯道,偏角α右=15°28′30″,半径R=600m,缓和曲线
长度Ls=70m, JD=K2+536.48。试计算曲线主点里程桩号。
1)曲线要素计算:
2)主点里程桩号计算:
以交点里程桩号为起算点:JD = K2+536.48
ZH = JD – T =K2+536.48 - 116.565 = K2+419.915
HY = ZH + Ls = K2+419.915 +70 = K2+489.915
QZ = ZH + L/2= K2+419.915+232.054/2 =K2+535.942
HZ = ZH + L = K2+419.915 +232.054 =K2+651.969
YH = HZ – Ls = K2+651.97 –70=K2+581.969
JD K2+536.48
-) T 116.565
ZH K2+419.915
+) Ls70
HY K2+489.915
+) L-2Ls 92.054
YH K2+581.969
+) Ls 70
HZ K2+651.969
-) L/2 232.054/2
QZ K2+535.942
+) J/2 1.077/2
JD K2+536.48
340.060024702422RLsp
996.346002407027024022323RLsLsq
565.116996.3422830.15)340.0250(2)(tgqtgpRT
054.232706002830.15180180LsRL
865.52502sec)340.0600(2sec)(RpRE
077.1054.232565.1162L2TJ
