超级全能生2018年3月理科
“超级全能生”2019高考全国卷26省9月联考甲卷-语文试题(含详细答案)

“超级全能生”2019高考全国卷26省9月联考甲卷语文注意事项:1.本试题共8页,满分150分,考试时间150分钟。
2.答题前,考生务必将自己的姓名、准考证号等填写在答题卡的相应位置。
3.全部答案在答题卡上完成,答在本试题上无效。
4.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
5.考试结束后,将本试题和答题卡一并交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1-3题。
近年来,关于汉语在各国持续升温的报道不断见诸国内外媒体。
语言是民族的重要特征之一,语言的影响力和传播力也日益成为民族国家综合实力的体现。
海外“汉语热”实际上反映的是中国合作共赢、大国担当和文化自信的国际魅力。
互利共赢是重要动力汉语难学,但挡不住学习的热情,海外汉语热出现的根本原因是中国综合国力和国际影响力的大幅度提升,经济上的互利共赢是推动海外汉语热的根本动力。
首先,海外中资企业对熟悉汉语的当地员工的需求越来越大,尤其是对从事国际贸易的企业来说,懂汉语的员工在录用和薪酬方面往往都具有较大优势。
择业方面的语言优势以引领和示范作用影响着海外青年的外语学习选择。
其次,中国游客海外旅游数量屡破新高,而且展现出强大的消费能力,“学说中国话”成为外国商铺每天必须面对的市场现实。
经济搭台,文化唱戏,一些从业人员开始有意识地了解中国文化,了解中国人的生活习惯、行为方式甚至文化传统。
同时,一些有远见的海外家庭看好中国的发展前景,着手培养下一代的汉语语言能力,认为掌握汉语能让孩子站在更好的起点。
由于学习汉语的主要难点是汉字识别和四声发音,需要耳濡目染,因此懂汉语的家政服务人员格外受欢迎,成为高级私教,收入明显高于普通家政服务人员。
为了保持不间断的汉语语言学习环境,这些家庭还在生活中大量使用智能语音服务或其他支持中外互译的手机软件。
专题12 利用导数解决函数的单调性-学会解题之高三数学万能解题模板【2022版】(原卷版)
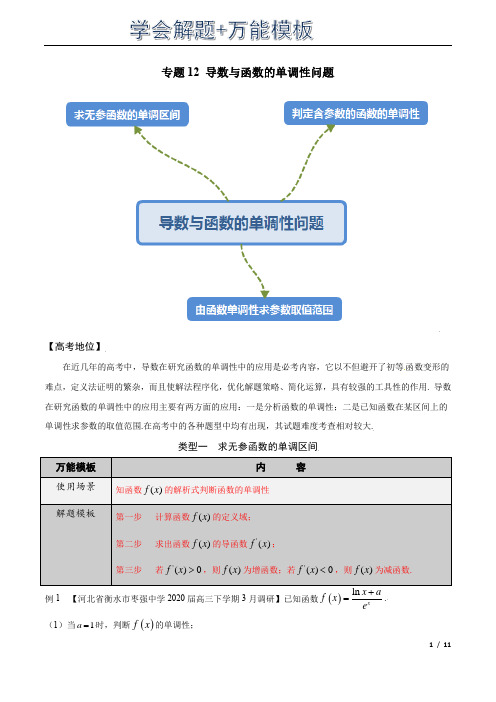
专题12 导数与函数的单调性问题【高考地位】在近几年的高考中,导数在研究函数的单调性中的应用是必考内容,它以不但避开了初等函数变形的难点,定义法证明的繁杂,而且使解法程序化,优化解题策略、简化运算,具有较强的工具性的作用. 导数在研究函数的单调性中的应用主要有两方面的应用:一是分析函数的单调性;二是已知函数在某区间上的单调性求参数的取值范围.在高考中的各种题型中均有出现,其试题难度考查相对较大.类型一 求无参函数的单调区间万能模板 内 容使用场景 知函数()f x 的解析式判断函数的单调性 解题模板第一步 计算函数()f x 的定义域; 第二步 求出函数()f x 的导函数'()f x ;第三步 若'()0f x >,则()f x 为增函数;若'()0f x <,则()f x 为减函数.例1 【河北省衡水市枣强中学2020届高三下学期3月调研】已知函数()ln xx af x e+=. (1)当1a =时,判断()f x 的单调性;【变式演练1】函数,的单调递增区间为__________.【来源】福建省三明第一中学2021届高三5月校模拟考数学试题【变式演练2】已知函数,则不等式的解集为___________.【来源】全国卷地区“超级全能生”2021届高三5月联考数学(文)试题(丙卷)【变式演练3】【黑龙江省哈尔滨六中2020届高三高考数学(文科)二模】已知函数()2sin f x x x =-+,若3(3)a f =,(2)b f =--,2(log 7)c f =,则,,a b c 的大小关系为( ) A .a b c <<B .b c a <<C .c a b <<D .a c b <<【变式演练4】【湖南省湘潭市2020届高三下学期第四次模拟考试】定义在R 上的连续函数()f x ,导函数为()f x '.若对任意不等于1-的实数x ,均有()()()10x f x f x '+->⎡⎤⎣⎦成立,且()()211x f x f x e -+=--,则下列命题中一定成立的是( )A .()()10f f ->B .()()21ef f -<-C .()()220e f f -<D .()()220e f f ->类型二 判定含参数的函数的单调性万能模板 内 容使用场景 函数()f x 的解析式中含有参数解题模板第一步 计算函数()f x 的定义域并求出函数()f x 的导函数'()f x ;第二步 讨论参数的取值范围,何时使得导函数'()f x 按照给定的区间大于0或小于0; 第三步 根据导函数的符号变换判断其单调区间.例2 【黑龙江省大庆市第四中学2020届高三下学期第四次检测】已知函数()()2ln 21f x x x ax a R =+-+∈.(1)讨论()f x 的单调性;【变式演练5】(主导函数是一次型函数)【福建省三明市2020届高三(6月份)高考数学(文科)模拟】已知函数()=1,f x nx ax a R -∈.(1)讨论函数f x ()的单调性;()2sin sin 2f x x x =⋅0,2x π⎡⎤∈⎢⎥⎣⎦()()2ln 1x xf x x e e -=+++()()2210f x f x --+≤【变式演练6】(主导函数为类一次型)【山东省威海荣成市2020届高三上学期期中考试】已知函数()x f x e ax -=+.(I )讨论()f x 的单调性;【变式演练7】(主导函数为二次型)【2020届山西省高三高考考前适应性测试(二)】已知函数()2ln af x x a x x=--,0a ≥. (1)讨论()f x 的单调性;【变式演练8】(主导函数是类二次型)【山西省太原五中2020届高三高考数学(理科)二模】已知函数2()(1)x f x k x e x =--,其中k ∈R.(1)当k 2≤时,求函数()f x 的单调区间;【变式演练9】已知函数,若在区间上单调递增,则的取值范围是( )A .B .C .D .【来源】江西省南昌市新建区第一中学2020-2021学年高三上学期期末考试数学(文)试题类型三 由函数单调性求参数取值范围万能模板 内 容使用场景 由函数单调性求参数取值范围解题模板第一步 计算函数()f x 的定义域并求出函数()f x 的导函数'()f x ; 第二步 根据题意转化为相应的恒成立问题; 第三步 得出结论.例3.【江苏省南通市2019-2020学年高三下学期期末】若()()21ln 242f x x b x =-++在()2,-+∞上是减函数,则实数b 的范围是( ) A .(],1-∞-B .(],0-∞C .(]1,0-D .[)1,-+∞【变式演练11】(转化为任意型恒成立)【四川省绵阳市2020高三高考数学(文科)三诊】函数2()(2)x f x e x ax b =-++在(1,1)-上单调递增,则2816a b ++的最小值为( )A .4B .16C .20D .18()22ln f x x x =-()f x ()2,1m m +m 1,14⎡⎫⎪⎢⎣⎭1,4⎡⎫+∞⎪⎢⎣⎭1,12⎡⎫⎪⎢⎣⎭[)0,1【变式演练12】(转化为变号零点)【山西省运城市2019-2020学年高三期末】已知函数2()ln 1f x x a x =-+在(1,2)内不是单调函数,则实数a 的取值范围是( ) A .[)2,8B .[]2,8C .(][),28,-∞+∞ D .()2,8【变式演练13】(直接给给定单调区间)【辽宁省六校协作体2019-2020学年高三下学期期中考试】已知函数()32113f x x mx nx =+++的单调递减区间是()3,1-,则m n +的值为( ) A .-4B .-2C .2D .4【变式演练14】(转化为存在型恒成立)【四川省仁寿第一中学北校区2019-2020学年高三月考】若f (x )321132x x =-++2ax 在(1,+∞)上存在单调递增区间,则a 的取值范围是( )A .(﹣∞,0]B .(﹣∞,0)C .[0,+∞)D .(0,+∞)【高考再现】1.(2021·全国高考真题(理))设2ln1.01a =,ln1.02b =, 1.041c =-.则( ) A .a b c <<B .b c a <<C .b a c <<D .c a b <<2.(2021·全国高考真题(理))已知且,函数.(1)当时,求的单调区间;(2)若曲线与直线有且仅有两个交点,求a 的取值范围. 3.已知函数. (1)讨论的单调性;(2)设,为两个不相等的正数,且,证明:. 【来源】2021年全国新高考Ⅰ卷数学试题 4.【2017山东文,10】若函数()e xf x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是A . ()2xf x -= B. ()2f x x = C. ()3xf x -= D. ()cos f x x =5.【2017江苏,11】已知函数31()2e ex x f x x x =-+-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,0a >1a ≠()(0)a x x f x x a=>2a =()f x ()y f x =1y =()()1ln f x x x =-()f x a b ln ln b a a b a b -=-112e a b<+<则实数a 的取值范围是 ▲ .6.【2020年高考全国Ⅰ卷文数20】已知函数()()e 2xf x a x =-+.(1)当1a =时,讨论()f x 的单调性; (2)若()f x 有两个零点,求a 的取值范围.7.【2020年高考全国Ⅰ卷理数21】已知函数()2e xf x ax x =+-.(1)当1a =时,讨论()f x 的单调性; (2)当0x ≥时,()3112f x x ≥+,求a 的取值范围. 8.【2020年高考全国Ⅱ卷文数21】已知函数()2ln 1f x x =+. (1)若()2f x x c ≤+,求c 的取值范围; (2)设0a >,讨论函数()()()f x f a g x x a-=-的单调性.9.(2018年新课标I 卷文)已知函数f (x )=ae x −lnx −1∈ (1)设x =2是f (x )的极值点.求a ,并求f (x )的单调区间; (2)证明:当a ≥1e 时,f (x )≥0∈10.【2018年全国普通高等学校招生统一考试理科数学(新课标I 卷)】已知函数f(x)=1x −x +alnx ∈ (1)讨论f(x)的单调性;(2)若f(x)存在两个极值点x 1,x 2,证明:f (x 1)−f (x 2)x 1−x 2<a −2.【反馈练习】1.【2020届广东省梅州市高三总复习质检(5月)】已知0x >,a x =,22xb x =-,()ln 1c x =+,则( )A .c b a <<B .b a c <<C .c a b <<D .b c a <<2.【2020届山东省威海市高三下学期质量检测】若函数()()()1cos 23sin cos 212f x x a x x a x =+++-在0,2π⎡⎤⎢⎥⎣⎦上单调递减,则实数a 的取值范围为( )A .11,5⎡⎤-⎢⎥⎣⎦B .1,15⎡⎤-⎢⎥⎣⎦C .[)1,1,5⎛⎤-∞-⋃+∞ ⎥⎝⎦D .(]1,1,5⎡⎫-∞-⋃+∞⎪⎢⎣⎭3.【河南省十所名校2019—2020学年高三毕业班阶段性测试】若函数()sin24sin f x x x m x =--在[0,2π]上单调递减,则实数m 的取值范围为( ) A .(2,2)-B .[2,2]-C .(1,1)-D .[1,1]-4.【黑龙江哈尔滨市第九中学2019-2020学年高三阶段验收】函数()3f x x ax =+,若对任意两个不等的实数()1212,x x x x >,都有()()121233f x f x x x ->-恒成立,则实数a 的取值范围是( ) A .()2,-+∞B .[)3,+∞C .(],2-∞-D .(),3-∞5.【湖北省武汉市新高考五校联合体2019-2020学年高三期中检测】若函数3211()232f x x x ax =-++ 在2,3⎡⎫+∞⎪⎢⎣⎭上存在单调增区间,则实数a 的取值范围是_______. 6.【四川省宜宾市2020届高三调研】若对(]0,1t ∀∈,函数2()(4)2ln g x x a x a x =-++在(,2)t 内总不是单调函数,则实数a 的取值范围是______7.【河南省南阳市第一中学校2019-2020学年高三月考】若函数()22ln f x x x =-在定义域内的一个子区间()1,1k k -+上不是单调函数,则实数k 的取值范围______.8.若函数在区间是增函数,则的取值范围是_________.【来源】陕西省宝鸡市眉县2021届高三下学期高考模拟文科数学试题 9.已知函数,若对任意两个不同的,,都有成立,则实数的取值范围是________________【来源】江西省景德镇市2021届高三上学期期末数学(理)试题10.【黑龙江省哈尔滨师范大学附属中学2020-2021学年高三上学期开学考试】(1)求函数()sin cos (02)f x x x x x π=+<<的单调递增区间;()cos 2sin f x x a x =+,62ππ⎛⎫⎪⎝⎭a ()()1ln 1xf x x x+=>1x 2x ()()1212ln ln f x f x k x x -≤-k(2)已知函数2()ln 43f x a x x x =-++在1,22⎡⎤⎢⎥⎣⎦上单调递增,求实数a 的范围.11.【黑龙江省哈尔滨三中2020届高三高考数学(文科)三模】函数()()21ln 1x f x x x -=-+. (1)求证:函数()f x 在()0,∞+上单调递增; (2)若m ,n 为两个不等的正数,求证ln ln 2m n m n m n->-+. 12.【湖北省黄冈中学2020届高三下学期适应性考试】已知函数()()ln 1ln f x ax x a x =-+,()f x 的导数为()f x '.(1)当1a >-时,讨论()f x '的单调性; (2)设0a >,方程()3f x x e =-有两个不同的零点()1212,x x x x <,求证121x e x e+>+. 13.【湖南省永州市宁远、道县、东安、江华、蓝山、新田2020届高三下学期六月联考】已知函数()()()ln 12f x a x x a =+-∈R .(1)讨论()f x 的单调性;(2)当0x ≥时,()1xf x e ≥-,求实数a 的取值范围.14.【2020届山西省高三高考考前适应性测试(二)】已知函数()xf x ae ex =-,()()ln 1xg x x b x e =--,其中,a b ∈R .(1)讨论()f x 在区间()0,∞+上的单调性; (2)当1a =时,()()0f x g x ≤,求b 的值.15.【河南省2020届高三(6月份)高考数学(文科)质检】已知函数2()22ln ()f x x ax x a R =-+∈.(1)讨论函数()f x 的单调性;(2)若()f x 存在两个极值点()1221,x x x x >,求证:()()()2121(2)f x f x a x x -<--. 16.【山东省2020年普通高等学校招生统一考试数学必刷卷】已知实数0a >,函数()22ln f x a x a x x=++,()0,10x ∈.(1)讨论函数()f x 的单调性;(2)若1x =是函数()f x 的极值点,曲线()y f x =在点()()11,P x f x ,()()22,Q x f x ()12xx <处的切线分别为12,l l ,且12,l l 在y 轴上的截距分别为12,b b .若12//l l ,求12b b -的取值范围.17.【福建省2020届高三(6月份)高考数学(理科)模拟】已知函数()()()2ln 222f x x a x x =++++,0a >.(1)讨论函数()f x 的单调性; (2)求证:函数()f x 有唯一的零点.18.【山东省潍坊市五县2020届高三高考热身训练考前押题】已知函数()f x 满足222(1)()2(0)2x f f x x f x e -'=+-,21()(1)24x g x f x a x a ⎛⎫=-+-+ ⎪⎝⎭,x ∈R . (1)求函数()f x 的解析式; (2)求函数()g x 的单调区间;(3)当2a ≥且1≥x 时,求证:1ln ln x e x e a x x--<+-.19.【陕西省商洛市商丹高新学校2020届高三下学期考前适应性训练】已知函数3()ln ()f x x a x a R =-∈.∈1)讨论函数()f x 的单调性∈∈2)若函数()y f x =在区间(1,]e 上存在两个不同零点∈求实数a 的取值范围.20.【2020年普通高等学校招生全国统一考试伯乐马模拟考试】已知函数()()22xxf x ax a e e =-++.(1)讨论函数()f x 的单调性; (2)若函数()()()2212x x g x f x ax x a e e =-++-存在3个零点,求实数a 的取值范围. 21.【金科大联考2020届高三5月质量检测】已知函数()()()()()22224ln 2144f x x ax x a x a a x a =--+++∈R .(∈)讨论函数()f x 的单调性;(∈)若0a ≤,证明:函数()f x 在区间)1,a e -⎡+∞⎣有且仅有一个零点.22.已知函数.(1)若,求函数的单调区间; (2)求证:对任意的,只有一个零点.【来源】全国Ⅱ卷2021届高三高考数学(理)仿真模拟试题 23.已知函数. (1)当时,判断的单调性;(2)若有两个极值点,求实数的取值范围.【来源】安徽省合肥六中2021届高三6月份高考数学(文)模拟试题 24.已知函数. (1)求的单调性;(2)设函数,讨论的零点个数. 【来源】重庆市高考康德卷2021届高三模拟调研卷数学试题(三) 25.已知函数, (1)讨论的单调性;(2)若,,,用表示,的最小值,记函数,,讨论函数的零点个数.【来源】山东省泰安肥城市2021届高三高考适应性训练数学试题(二) 26.已知() (1)讨论的单调性;(2)当时,若在上恒成立,证明:的最小值为. 【来源】贵州省瓮安中学高三2021届6月关门考试数学(理)试题27.已知函数.(1)讨论的单调性;()321()13f x x a x x =--+2a =-()f x a ∈R ()f x ()21ln 2f x x ax x ax =-+1a =()f x ()f x a ()()cos sin ,0,2f x x x x x π=-∈()f x ()()(01)g x f x ax a =-<<()g x ()ln()xf x x a x a=+-+a R ∈()f x 4a =()1cos (2sin )2g x x x mx x =++0m >}{min ,m n m n }{()min ()()h x f x g x =,[],x ππ∈-()h x ()ln f x x ax =+a R ∈()f x 1a =()()1f x k x b ≤++()0,∞+221k b k +--1e -+2()2ln ,()f x x ax x a R =+++∈()f x(2)若恒成立,求的最大值.【来源】广东省佛山市五校联盟2021届高三5月数学模拟考试试题 28.已知函数. (1)若,证明:在单调递增; (2)若恒成立,求实数的取值范围.【来源】黑龙江省哈尔滨市第三中学2021届高三五模数学(理)试题 29.已知函数. (1)若在上为增函数,求实数a 的取值范围;(2)设,若存在两条相互垂直的切线,求函数在区间上的最小值.【来源】四川省达州市2021 届高三二模数学(文)试题 30.已知函数. (1)如果函数在上单调递减,求的取值范围; (2)当时,讨论函数零点的个数.【来源】内蒙古赤峰市2021届高三模拟考试数学(文)试题 31.已知函数. (1)若在R 上是减函数,求m 的取值范围;(2)如果有一个极小值点和一个极大值点,求证 有三个零点. 【来源】安徽省淮南市2021届高三下学期一模理科数学试题32.已知函数.(1)若函数在上为增函数,求实数的取值范围; (2)当时,证明:函数有且仅有3个零点. 【来源】重庆市第二十九中学校2021届高三下学期开学测试数学试题()xf x e ≤a ()ln x f x xe ax a x =--0a ≤()f x ()0,∞+()0f x ≥a 21()cos 2f x x ax x =++()f x [0,)+∞21()()2g x f x x =-()g x sin ()1()x g x F x x -+=,2ππ⎡⎤⎢⎥⎣⎦1()ln(1)1f x a x x =-+-()()22g x f x x =-+(1,)+∞a 0a >()y f x =21()e 1()2x f x x mx m =+-+∈R ()f x ()f x 1x 2x ()f x ()e sin 1xf x ax x =-+-()f x ()0,∞+a 12a ≤<()()()2g x x f x =-11/ 11。
第一单元 生活智慧与时代精神

是一种客观存在(但不是客观实在,因为客观实在是相对于
意识而存在的),哲学要进行反思,既需要对实践活动进行
反思,也需要针对以往的某些思想、认识进行反思,这都是
坚持一切从实际出发,实事求是的体现,这并不是唯心主义
的表现,故这一表述不妥。
4.有人说哲学研究人生问题,有人说哲学研究认识问题,其实
哲学只研究思维与存在的关系。
6.作家周国平说:如果应试、谋职、赚钱是有用,那么,哲学的确
没有什么用。可如果你希望成为一个真正优秀的人,哲学恰恰是
最有用的。哲学是“无用之学”有大用,这是因为
()
①哲学是具体科学进步的基础 ②哲学是世界观和方法论的统一
③哲学既是高度的抽象又是丰富的具体
④哲学揭示了最一般的本质和最普遍的规律
A.①③ C.②③
2.(2020·浙江 7 月选考)人的世界观受自己生活世界的制约。( T )
理由:世界观是人们对于整个世界的总的看法和根本观点。作为
社会意识,世界观由社会存在决定,必然要受到人们自己生活世
界的制约。因而,题中说法正确。
3.哲学与具体科学的关系是整体与部分的关系。
( F)
理由:本题考查哲学与具体科学的关系。哲学与具体科学是共性
B.①④ D.②④
解析:哲学是“无用之学”有大用,指的是哲学能给具体科学以 高层次指导,根源在于哲学是世界观和方法论的统一,揭示了最 一般的本质和最普遍的规律,②④正确。具体科学是哲学进步的 基础,①错误。哲学是对万事万物共性和本质规律的高度抽象概 括,不是具体的,③错误。
答案:D
7.(2020·5 月稽阳联考)160 多年前,达尔文的生物进化论不仅是生物
唯 基本 唯心主义认为,意识是本原的,物质依赖于意
立体几何中的探索性问题求解策略(原卷版)

专题35 立体几何中的探索性问题求解策略【高考地位】立体几何中的探索性问题是高考几何的一个难点,尤常见于新高考的多选题中,其题目特点是灵活性较强,需要相对丰富的空间想象能力及计算能力,对所研究几何体进行深入的剖析与推理,其常见类型有两种:一、空间中位置关系的探索;二、空间角的探索.类型一空间中位置关系的探索方法一几何法-的所有棱长均为E,F分别是PC,AB的中点,M为棱PB上异于P,例1已知正四棱锥P ABCDB的一动点,现有以下结论:①线段EF的长度是△②EMF③存在点M使得PB⊥平面MEF;④EMF∠始终是钝角.其中不正确的结论共有()A.1个B.2个C.3个D.4个【来源】河北省沧州市2021届高三三模数学试题【变式演练1】(多选)在直角三角形ABC 中,∠B =2π,AC =2BC =4,D 为线段AC 的中点,如图,将∠ABD 沿BD 翻折,得到三棱锥P ﹣BCD (点P 为点A 翻折到的位置),在翻折过程中,下列说法正确的是( )A .∠PBD 的外接圆半径为2B .存在某一位置,使得PD ∠BDC .存在某一位置,使得PB ∠CDD .若PD ∠DC ,则此时三棱锥P ﹣BCD 的外接球的体积为323π 【来源】山东省百师联盟2021届高三二轮联考数学试题(二)方法二 向量法例2、3.已知长方体1111ABCD A B C D -中,12BB AB BC ==,点E 在线段1CC 上,()101CC λλ=≤≤平面α过线段1AA 的中点以及点1B 、E ,现有如下说法: (1)[]0,1λ∃∈,使得1BE B E ⊥;(2)若12,23λ⎡⎤∈⎢⎥⎣⎦,则平面α截长方体1111ABCD A B C D -所得截面为平行四边形;(3)若0λ=,2AB =,则平面α截长方体1111ABCD A B C D -所得截面的面积为以上说法正确的个数为( ) A .0B .1C .2D .3【来源】全国一卷2021届高中毕业班考前热身联合考试理科数学试题例3、(多选)在棱长固定的正方体1111ABCD A B C D -中,点E ,F 分别满足AE AB λ=,([0,1],[0,1])BF BC μλμ=∈∈,则( )A .当12μ=时,三棱锥11A B EF -的体积为定值 B .当12μ=时,存在λ使得1BD ⊥平面1B EF C .当12λ=时,点A ,B 到平面1B EF 的距离相等 D .当λμ=时,总有11A F C E ⊥【来源】江苏省苏州市2021-2022学年高三上学期期初调研数学试题【变式演练2】(多选)在棱长为1的正方体1111ABCD A B C D -中,点E 为线段1CD 上一动点(不包含端点),则下列说法正确的有( )A .1AB ⊥平面11A D EB .1DE A E +的最小值为1C .存在点E 使得1DE AD ⊥D .点D 到平面11A DE 【来源】全国新高考2021届高三数学方向卷试题(A )【变式演练3】如图所示,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AB AD ⊥,//AB CD ,24AB AD PA CD ====,G 为PD 的中点.(1)求证AG ⊥平面PCD ;(2)若点F 为PB 的中点,线段PC 上是否存在一点H ,使得平面GHF ⊥平面PCD ?若存在,请确定H 的位置;若不存在,请说明理由.【来源】湖北省恩施州2021-2022学年高三上学期第一次教学质量监测数学试题类型二 空间角的探索 方法一 几何法例3.如图,矩形ABCD 中,已知2,4,AB BC E ==为BC 的中点.将ABE △沿着AE 向上翻折至MAE 得到四棱锥M AECD -.平面AEM 与平面AECD 所成锐二面角为α,直线ME 与平面AECD 所成角为β,则下列说法错误的是( )A .若F 为AD 中点,则ABE △无论翻折到哪个位置都有平面AEM ⊥平面MBFB .若Q 为MD 中点,则ABE △无论翻折到哪个位置都有//CQ 平面AEM Csin αβ=Dcos αβ=【来源】湖北省武汉市华中师范大学第一附属中学2021届高三下学期5月高考押题卷文科数学试题 【变式演练4】(多选)在棱长为1的正方体1111ABCD A B C D -中,点P 满足1DP DD DA λμ=+,[0,1]λ∈,[0,1]μ∈,则以下说法正确的是( )A .当λμ=时,//BP 平面11CB D B .当12μ=时,存在唯一点P 使得DP 与直线1CB 的夹角为3π C .当1λμ+=时,CPD .当1λμ+=时,CP 与平面11BCC B 所成的角不可能为3π 【来源】湖北省恩施州2021-2022学年高三上学期第一次教学质量监测数学试题方法二 向量法例4.如图1,菱形ABCD 中120ABC ∠=︒,动点E ,F 在边AD ,AB 上(不含端点),且存在实数λ使EF BD λ→→=,沿EF 将AEF 向上折起得到PEF ,使得平面PEF ⊥平面BCDEF ,如图2所示.(1)若BF PD ⊥,设三棱锥P BCD -和四棱锥P BDEF -的体积分别为1V ,2V ,求12V V ;(2)试讨论,当点E 的位置变化时,二面角E PF B --是否为定值,若是,求出该二面角的余弦值,若不是,说明理由.【来源】重庆市南开中学2021届高三下学期第六次质量检测数学试题【变式演练5】O 中,平行四边形ABCD 是圆O 的内接四边形,AD ,点P 是半球面上的动点,且四棱锥P ABCD -的体积为83.(1)求动点P 的轨迹T 围成的面积;(2)是否存在点P 使得二面角P AD B --的大小为3π?请说明理由. 【来源】山西省临汾市2021届高三下学期二模数学(理)试题【高考再现】1.(2018年全国卷Ⅲ文数高考试题)如图,矩形ABCD 所在平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得MC ∥平面PBD ?说明理由.【反馈练习】1.(多选)已知梯形ABCD ,112AB AD BC ===,//AD BC ,AD AB ⊥,P 是线段BC 上的动点;将ABD △沿着BD 所在的直线翻折成四面体A BCD ',翻折的过程中下列选项中正确的是( )A .不论何时,BD 与A C '都不可能垂直B .存在某个位置,使得A D '⊥平面A BC ' C .直线A P '与平面BCD 所成角存在最大值 D .四面体A BCD '的外接球的表面积的最小值为4π【来源】广东省佛山市五校联盟2021届高三5月数学模拟考试试题2.(多选)已知某正方体的平面展开图如图所示,点E ,G 分别是棱BC ,BQ 的中点,F 是棱CR (不包含端点)上的动点,则下列说法正确的是( )A .四面体AEFP 的体积为定值B .存在点F 使得PC ⊥平面AEF C .存在点F 使得//PG 平面AEFD .当F 为棱CR 的中点时,平面AEF 截正方体所得上、下两个几何体的体积之比为17:7 【来源】2021新高考高考最后一卷数学第三模拟3.(多选)在棱长为1的正方体1111ABCD A B C D -中,已知E 为线段1B C 的中点,点F 和点P 分别满足111D F DC λ=,11D P D B μ=,其中,[0,1]λμ∈,则下列说法正确的是( ) A .当λ=12时,三棱锥P -EFD 的体积为定值 B .当µ=12时,四棱锥P -ABCD 的外接球的表面积是34πC .PE PF +D.存在唯一的实数对(,)λμ,使得EP∠平面PDF【来源】广东省2022届高三上学期新高考普通高中联合质量测评摸底数学试题4.如图,矩形BDEF所在平面与正方形ABCD所在平面互相垂直,2DB DE=,点P在线段EF上.给出下列命题:①直线PD⊥直线AC;②直线PD与平面ABCD所成角的正弦值的取值范围是⎤⎥⎣⎦;③存在点P,使得直线PD⊥平面ACF;④存在点P,使得直线//PD平面ACF.其中所有真命题的序号是______.【来源】四川省大数据精准联盟2021届高三第三次统一监测文科数学试题5.七面体玩具是一种常见的儿童玩具.在几何学中,七面体是指由七个面组成的多面体,常见的七面体有六角锥、五角柱、正三角锥柱、Szilassi多面体等.在拓扑学中,共有34种拓扑结构明显差异的凸七面体,它们可以看作是由一个长方体经过简单切割而得到的.在如图所示的七面体EABCFD中,EA⊥平面,//,//,,2, 4.ABCD EA FC AD BC AD AB AD AB BC FC EA⊥=====(1)在该七面体中,探究以下两个结论是否正确.若正确,给出证明;若不正确,请说明理由:①//EF平面ABCD;②AF⊥平面EBD;(2)求该七面体的体积.【来源】广东省珠海市第二中学2021届考前模拟数学试题6.如图,ABC 为正三角形,半圆O 以线段BC 为直径,D 是圆弧BC 上的动点(不包括B ,C 点)平面ABC ⊥平面BCD .(1)是否存在点D ,使得BD AC ⊥?若存在,求出点D 的位置,若不存在,请说明理由; (2)30CBD ∠︒=,求直线AC 与平面ABD 所成角的正弦值. 【来源】百强名校2021届高三5月模拟联考(A 卷)理科数学试题7.在滨海文化中心有天津滨海科技馆,其建筑有鲜明的后工业风格,如图所示,截取其中一部分抽象出长方体和圆台组合,如图所示,长方体1111ABCD A B C D -中,14,2AB AD AA ===,圆台下底圆心O 为AB 的中点,直径为2,圆与直线AB 交于,E F ,圆台上底的圆心1O 在11A B 上,直径为1.(1)求1A C 与平面1A ED 所成角的正弦值; (2)求二面角1E A D F --的余弦值;(3)圆台上底圆周上是否存在一点P 使得1FP AC ⊥,若存在,求点P 到直线11A B 的距离,若不存在则说明理由.【来源】天津市河东区2021届高三下学期一模数学试题8.如图,已知矩形ABCD 所在平面垂直于直角梯形ABPE 所在平面,且2AB BP ==,1AD AE ==,AE AB ⊥,且//.AE BP(1)设点M 为棱PD 中点,求证//EM 平面ABCD ;(2)线段PD 上是否存在一点N ,使得直线BN 与平面PCD ?若存在,试求出线段PN 的长度;若不存在,请说明理由.【来源】湖北省新高考联考协作体2021-2022学年高三上学期新起点考试数学试题9.如图,在三棱柱111ABC A B C -中,1AA ⊥平面111A B C ,12AB BC AC A A ====,E ,F 分别为11A C ,11B C 的中点.(∠)在四边形11ABB A 内是否存在点G ,使平面//GEF 平面1ABC ?若存在,求出该点的位置;若不存在,请说明理由;(∠)设D 是1CC 的中点,求DA 与平面1ABC 所成角θ的正弦值.【来源】“超级全能生”2021届高三3月份高考数学(理)联考试题(丙卷)10.在四棱锥S ABCD -中,底面ABCD 为菱形,60BAD ∠=︒,平面SAD ⊥平面ABCD ,SAD 是边长为2的正三角形,E ,F 分别为AD ,SB 的中点. (∠)证明://EF 平面SCD ;(∠)在棱SA 上是否存在一点P ,使得锐二面角P BC S --若存在,求出SP SA 的值;若不存在,请说明理由.【来源】2021届高三数学临考冲刺原创卷(三)。
第八课 唯物辩证法的发展观

考点 1 完成时,因为发展是永恒的
主题。
(T)
理由:人类社会是一个不断发展的过程,发展的实质是前进和
上升,发展是永恒的主题,因此中国的改革开放只有进行时没
有完成时。
2.新事物总是在旧事物的母体中孕育产生。
( T)
理由:新事物与旧事物有着密切联系,新事物总是在旧事物的
B.②③
C.③④
D.①④
解析:题意强调不能过分看重结果,这是因为没有量变的积累, 结果很难达到预期,这告诉我们要重视量的积累,因为量变是 质变的必要准备,故①④正确。不在乎结果与不在乎过程都是 不应该的,故②③不选。 答案:D
6.习近平主席发表新年贺词时,在列举了我国取得的主要成
就后,他指出,这说明,只要坚持,梦想总是可以实现的。
答案:C
5.事物的运动、变化与发展的区别在于
()
A.运动、变化是看得见的,发展是看不见的
B.运动、变化是倒退的,发展是前进的
C.运动、变化既可能是前进的,也可能是倒退的,而发展则是
前进、上升的变化
D.运动、变化是旧事物的变化,发展则是前进、上升的变化
解析:A 错误,运动、变化与发展不能用看得见和看不见来划分;
答案:A
4.共享单车的出现打破了以往公共自行车固定车位的束缚,使
用十分方便,广受市民欢迎。但是,随着投放量的不断增大,
乱停乱放等问题日益显现。这告诉我们
()
①事物发展的道路是曲折的 ②矛盾的普遍性包含特殊性
③矛盾双方既相互对立又相互统一 ④量变达到一定程度
必然引起质变
A.①②
B.②④
C.①③
D.③④
①事物发展的前途、 2017·11 月选考 T29·考查事物发展的道路
2018年高考理综真题(全国三卷)

2018年高考理综试题及答案(全国卷3)1.下列研究工作中由我国科学家完成的是A.以豌豆为材料发现性状遗传规律的实验B.用小球藻发现光合作用暗反应途径的实验C.证明DNA是遗传物质的肺炎双球菌转化实验D.首例具有生物活性的结晶牛胰岛素的人工合成2.下列关于细胞的结构和生命活动的叙述,错误的是A.成熟个体中的细胞增殖过程不需要消耗能量B.细胞的核膜、内质网膜和细胞膜中都含有磷元素C.两个相邻细胞的细胞膜接触可实现细胞间的信息传递D.哺乳动物造血干细胞分化为成熟红细胞的过程不可逆3.神经细胞处于静息状态时,细胞内外K+和Na+的分布特征是A.细胞外K+和Na+浓度均高于细胞内B.细胞外K+和Na+浓度均低于细胞内C.细胞外K+浓度高于细胞内,Na+相反D.细胞外K+浓度低于细胞内,Na+相反4.关于某二倍体哺乳动物细胞有丝分裂和减数分裂的叙述,错误的是A.有丝分裂后期与减数第二次分裂后期都发生染色单体分离B.有丝分裂中期与减数第一次分裂中期都发生同源染色体联会C.一次有丝分裂与一次减数分裂过程中染色体的复制次数相同D.有丝分裂中期和减数第二次分裂中期染色体都排列在赤道板上5.下列关于生物体中细胞呼吸的叙述,错误的是A.植物在黑暗中可进行有氧呼吸也可进行无氧呼吸B.食物链上传递的能量有一部分通过细胞呼吸散失C.有氧呼吸和无氧呼吸的产物分别是葡萄糖和乳酸D.植物光合作用和呼吸作用过程中都可以合成ATP6.某同学运用黑光灯诱捕的方法对农田中具有趋光性的昆虫进行调查,下列叙述错误的是A.趋光性昆虫是该农田生态系统的消费者B.黑光灯传递给趋光性昆虫的信息属于化学信息C.黑光灯诱捕的方法可用于调查某种趋光性昆虫的种群密度D.黑光灯诱捕的方法可用于探究该农田趋光性昆虫的物种数目7.化学与生活密切相关。
下列说法错误的是A.泡沫灭火器可用于一般的起火,也适用于电器起火B.疫苗一般应冷藏存放,以避免蛋白质变性C.家庭装修时用水性漆替代传统的油性漆,有利于健康及环境D.电热水器用镁棒防止内胆腐蚀,原理是牺牲阳极的阴极保护法8.下列叙述正确的是A.24g镁与27g铝中,含有相同的质子数B.同等质量的氧气和臭氧中,电子数相同C.1mol重水与1mol水中,中子数比为2∶1D.1mol乙烷和1mol乙烯中,化学键数相同9.苯乙烯是重要的化工原料。
2020届高三大数据精华浓缩训练卷(四)
2020届高三大数据精华浓缩训练卷(浙江版)专题04 大数据精华浓缩训练卷之浙江卷(4)选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【浙江省温州市2019-2020学年高三11月适应性测试一模】已知全集{1,2,3,4}U =,{1,3}A =,{,3}C 2U B =,则A B =I ( )A .{1}B .{3}C .{4}D .{1,3,4}【答案】A 【解析】因为{1,2,3,4}U =,{,3}C 2U B = 所以由补集定义与运算可得{1,4}B = 又因为{1,3}A =根据交集运算可得{1,3}14{}}{1,A B ==I I 故选:A2.【浙江省2019年高考模拟训练卷】已知双曲线2222:1x y C a a-=,则C 的离心率是( )A BC .2D 【答案】B 【解析】∵双曲线方程为2222:1x y C a a-=,∴双曲线为等轴双曲线,∴故选B.3.【浙江省温州市2019届高三2月高考适应性测试】以下不等式组表示的平面区域是三角形的是( )A.B.C.D.【答案】D【解析】A选项:表示的区域如图:不满足题意;B选项:表示的区域如图:不满足题意;C选项:表示的区域如图:不满足题意;D选项:表示的区域如图:满足题意;故选D.4.【浙江省温州九校2019届高三第一次联考】如图,某几何体三视图(单位:)为三个直角三角形,则该几何体的体积为()A.B.C.D.【答案】B【解析】根据几何体的三视图,得;该几何体是底面为直角三角形,高为1的三棱锥,∴该几何体的体积为故选:B .5.【2019年10月浙江省金丽衢十二校零模】己知a ,b 是实数,则“2a >且2b >”是“4a b +>且4ab >”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】A 【解析】因为“2a >且2b >”⇒ “4a b +>且4ab >” “4a b +>且4ab >”¿“2a >且2b >”所以“2a >且2b >”是“4a b +>且4ab >”的充分而不必要条件 故选A6.【2019年9月浙江省超级全能生高三第一次联考】在同一直角坐标系中,函数2y ax bx =+,x b y a-=(0a >且1a ≠)的图象可能是()A .B .C .D .【答案】D 【解析】对1a >和01a <<分类讨论,当1a >时,对应A,D:由A 选项中指数函数图象可知,002bb a>∴-<,A 选项中二次函数图象不符,D 选项符合;当01a <<时,对应B,C:由指数函数图象可知,00,02bb a a<∴->>,则B ,C 选项二次函数图象不符,均不正确,故选D . 7.【浙江省杭州市第二中学2018届高三6月热身考】若随机变量满足,,则下列说法正确的是 A . B . C . D .【答案】D【解析】 随机变量满足,,则:,据此可得:. 本题选择D 选项.8.【2019年浙江省名校新高考研究联盟(Z20联盟)高三上学期第一次联考】在矩形ABCD 中,4AB =,3AD =,E 为边AD 上的一点,1DE =,现将ABE ∆沿直线BE 折成A BE ∆',使得点A '在平面BCDE上的射影在四边形BCDE 内(不含边界),设二面角A BE C '--的大小为θ,直线A B ','A C 与平面BCDE 所成的角分别为,αβ,则( )A .βαθ<<B .βθα<<C .αθβ<<D .αβθ<<【答案】D 【解析】如图所示,在矩形ABCD 中,过A 作AF BE ⊥交于点O ,将ABE ∆沿直线BE 折成A BE ∆',则点A '在面BCDE 内的射影'O 在线段OF 上,设A '到平面BCDE 上的距离为h ,则''h AO =,由二面角、线面角的定义得:'tan h O O θ=,'tan h O B α=,'tan hO Cβ=, 显然'''',O O O B O O O C <<,所以tan θ最大,所以θ最大, 当'O 与O 重合时,max (tan )h OB α=,min (tan )h OCβ=,因为h OB <h OC,所以max (tan )α<min (tan )β,则tan tan αβ<,所以αβ<, 所以αβθ<<,故选D.9.【浙江省金华十校2018年4月高考模拟】已知平面内任意不共线三点,,,则的值为( )A .正数B .负数C .0D .以上说法都有可能 【答案】B 【解析】.即的值为负数.本题选择B 选项.10.【2020届浙江省绍兴市柯桥区高三上学期期末】已知数列{}n a 满足101a <<,()142n n n a ta t R a ++=∈+,若对于任意*n N ∈,都有103n n a a +<<<,则t 的取值范围是( ) A .(]1,3- B .[]0,3C .()3,8D .()8,+∞【答案】B 【解析】用排除法:当3t =时,1432n n n a a a ++=+,明显有0n a >,下面用数学归纳法证明3n a <, 当1n =时,1013a <<<,成立; 假设当n k =时,3k a <成立,则当1n k =+时,143554432232k k k k a a a a ++==-<-=+++,所以当1n k =+时,13k a +<成立, 综上:对任意*n N ∈,都有3n a <;另外()21(3)1434320222n n n n n n n n n n n n a a a a a a a a a a a a +-++++---=-==>+++, 所以1n n a a +<,所以当3t =时,103n n a a +<<<恒成立,排除CD ;当12t =-时,14212n n n a a a +=+-,若1n =,则1214122a a a -=+,因为101a <<,此时20a <是有可能的,故排除A , 故选:B.非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.【2020届浙江省绍兴市柯桥区高三上学期期末】已知复数11z i =-,122z z i ⋅=-,则复数2z =______. 【答案】32i + 【解析】 设2z a bi =+,则12(1)()()()2z z i a bi a b b a i i ⋅=-+=++-=-,21a b b a +=⎧∴⎨-=-⎩,解得3212a b ⎧=⎪⎪⎨⎪=⎪⎩,232z i∴=+, 故答案为:32i+.12.【浙江省金华十校2019届高三上学期期末联考】已知复数z 的共轭复数12iz i+=-,则复数z 的虚部是______,z =______.【答案】35- 5【解析】解:由()()()()1211322255i i i z i i i i +++===+--+, 可得1355z i =-, ∴复数z 的虚部是35-,z ==故答案为:35-;5. 13.【2019年浙江省名校新高考研究联盟(Z20联盟)高三上学期第一次联考】若7280128(2)(21)x x a a x a x a x +-=++++L ,则0a =______,2a =_____.【答案】–2 –154 【解析】令0x =得:02a =-,展开式中含2x 项为:(1)当(2)x +出x ,7(21)x -出含x 项,即1617(2)(1)T x C x =⋅⋅⋅-; (2)当(2)x +出2,7(21)x -出含2x 项,即225272(2)(1)T C x =⋅⋅⋅-; 所以2a =1277224(1)154C C ⋅+⋅⋅⋅-=-,故填:2-;154-.14.【浙江省杭州地区(含周边)重点中学2019-2020学年高三上学期期中】已知角α的终边经过点(P -,则tan α=_________,sin()cos()2ππαα+-=_________.【答案】 34- 【解析】由任意角的三角函数的定义可知tan α==sin()sin παα+=-,cos()cos ()cos()sin 222πππαααα⎡⎤-=--=-=⎢⎥⎣⎦所以223sin()cos()sin 24ππααα⎡⎤⎢⎥+-=-=-=-故答案为:34-15.【浙江省宁波市宁波十校2019-2020学年高三上学期11月月考】已知椭圆221106x y +=,倾斜角为60°的直线与椭圆分别交于A 、B 两点且AB =,点C 是椭圆上不同于A 、B一点,则△ABC 面积的最大值为_____.【解析】由题意,设直线AB 的方程为y m =+,点 A (x 1,y 1),B(x 2,y 2), 联立方程组221106y mx y ⎧=+⎪⎨+=⎪⎩,整理得18x 2+5m 2﹣30=0,所以x 1+x 29-=,x 1x 2253018m -=.因为AB ==, 代入整理得24m =,解得2m=±, 不妨取:m =2,可得直线AB 的方程为2y =+,设与直线AB 平行且与椭圆相切的直线方程为y =+t ,联立方程组221106y t x y ⎧=+⎪⎨+=⎪⎩,整理得18x 2tx +5t 2﹣30=0,由△=300t 2﹣72×(5t 2﹣30)=0,解得:t =±6. 取t =﹣6时,与直线AB 平行且与椭圆相切的直线与直线AB的距离4d ==,所以△ABC 面积的最大值12S d AB=142=⨯=,故答案为:9. 16.【浙江省杭州地区(含周边)重点中学2019-2020学年高三上学期期中】设1a >,曲线()xf x a =与曲线()log a g x x =有且仅有一个公共点,则实数a 的值是________. 【答案】1e e 【解析】因为指数函数()xf x a =与对数函数()log a g x x =互为反函数 所以()xf x a =与()log a g x x =关于直线y x =对称由于1a >时,曲线()xf x a =与曲线()log a g x x =有且仅有一个公共点则公共点在直线y x =上即函数()xf x a =,1a >与直线y x =只有一个交点即0x a x -=只有一个根 令()xh x a x =-,1a >()ln 1x h x a a '=-当()log ln a x a >-时,()0h x '> 当()log ln a x a <-时,()0h x '<所以函数()h x 在区间()(,log ln )a a -∞-上单调递减,在区间()()log ln ,a a -+∞上单调递增所以函数()h x 的最小值()()()log ln (log ln )=log ln 0a a a a h a aa --+=即()1ln ln 110ln(ln )1ln ln ln e a a a a e a a e+=⇒=-⇒=⇒= 故答案为:1e e17.【2019年9月浙江省超级全能生高三第一次联考】已知数列{}n a ,满足()21n n na k a a +=-.若1112a k ==,则1n n a a +⎧⎫⎨⎬⎩⎭的最小值是___________,若12a =,且存在常数0M >,使得任意n a M ≤,则k 的取值范围是______________.【答案】12[]11-,【解析】(1)令1y n n x a a +==,,2y x x =-,1n n a a +表示点()1n n a a +,与原点连线的斜率,因为112a =,所以1(0,]2n a ∈,由于()12a a ,为21,(0,]2x y x x ∈=-最高点,所以21a a 最小,等于12.(2)当0k =时,显然存在;当0k ≠时,由12a =,则2M≥ ,由2()y k x x =-图象可知,使得任意n a M ≤成立,则需2,4(),k M k M M M ⎧≤⎪⎨⎪-≤⎩即4,1,1k M k M ⎧≤⎪⎨≤⎪-⎩ 又14(2)1M M M >≥-,所以111k M ≤≤-,故k 的取值范围是11k -≤≤.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.【浙江省杭州市西湖区杭州学军中学2019-2020学年高三上学期期中】已知在ABC △中,1AB =,2AC =.(1)若BAC ∠的平分线与边BC 交于点D ,求()2AD AB AC ⋅-u u u r u u u r u u u r;(2)若点E 为BC 的中点,求2211AE BC+u u u r u u u r 的最小值. 【答案】(1)0;(2)910【解析】(1)因为AD 是角平分线,从而得到12BD AB CD AC ==u u u r u u u r u u u r u u u r 所以可得2133AD AB AC =+u u u r u u u r u u u r,所以()21233AD AB AC AB AC ⎛⎫⋅-=+ ⎪⎝⎭u u u r u u u r u u u r u u ur u u u r ()20AB AC ⋅-=u u u r u u u r ;(2)在ABE ∆和ACE ∆由用余弦定理可得222cos 2AE BE AB AEB AE BE +-∠=u u u r u u u r u u u r u u u r u u u r ,222cos 2AE CE ACAEC AE CE+-∠=u u u r u u u r u u u r u u u r u u u r, 而BE CE =u u u r u u u r,cos cos AEB AEC ∠=-∠,所以得到22222222AE BE AB AE CE ACAE BE AE CE+-+-=-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r整理得:224AE BC +u u u r u u u r ()22210AB AC =+=u u u r u u u r22221111110AE BC AE BC ⎛⎫ ⎪∴+=+ ⎪ ⎪⎝⎭u u u r u u u r u u u r u u u r ()224AE BC +u u ur u u u r2222414110BC AEAE BC ⎡⎤⎢⎥=+++⎢⎥⎢⎥⎣⎦u u u r u u u r u u u r u u u r1951010⎛+= ⎝≥ 当且仅当2BC AE =u u u r u u u r时,等号成立.19.【浙江省宁波市宁波十校2019-2020学年高三上学期11月月考】如图,四边形ABCD 为菱形,四边形ACFE 为平行四边形,设BD 与AC 相交于点G ,AB =BD =AE =2,∠EAD =∠EAB .(1)证明:平面ACFE ⊥平面ABCD ;(2)若直线AE 与BC 的夹角为60°,求直线EF 与平面BED 所成角的余弦值. 【答案】(1)证明见解析(2)13【解析】(1)证明:连接EG ,因为AB =BD =AE =2,∠EAD =∠EAB , 可得△EAD ≌EAB ,∴ED =EB .∵G 为BD 的中点,所以EG ⊥BD ,因为四边形ABCD 为菱形,∴AC ⊥BD , ∴BD ⊥平面ACEF ,因为BD ⊂平面ABCD ; ∴平面ACFE ⊥平面ABCD ;(2)因为EF ∥AG ,直线EF 与平面BED 所成角即为AG 与平面BED 所成角; 以G 为原点建立如图所示空间直角坐标系,如图所示, 设E (a ,0,b )则AE =u u u r(a 3,0,b ), 因为BC =u u u r3,﹣1,0),所以由条件可得:|AE u u u r |2=(a 32+b 2=4且AE u u u r •3BC =-u u ur +3=2×2×cos 60°=2;解得3263a b ⎧=⎪⎪⎨⎪=⎪⎩,所以BE =u u u r 3126),因为DB =u u u r (0,2,0);所以可取平面BED 的法向量n =r(22,0,﹣1),因为EF AC ==u u u r u u u r(﹣23,0,0),设直线EF 与平面BED 所成角为θ,则sinθ22n EF n EF⋅==⋅u u ur r u u u r r ,∵0<θ2π≤;∴sosθ2113sin θ=-=; 既直线EF 与平面BED 所成角的余弦值为13.20.【2019年浙江省十校联盟高三上学期10月联考】已知等差数列{}n a 的前n 项和为()*n S n ∈N,且164a a a +=,69S =.数列{}n b 满足12b =,()1*122,n n n b b n n ---=≥∈N .(Ⅰ)求数列{}n a 和{}n b 的通项公式;(Ⅱ)求数列{}n n a b 的前n 项和n T ,并求n T 的最小值.【答案】(Ⅰ)39n a n =-,2n n b =;(Ⅱ)1(312)224n n T n +=-⨯+,最小值2324T T ==-.【解析】(Ⅰ)由()()6163443339S a a a a a =+=+==,得43a =,30a =. 故{}n a 的公差3d =,()3339n a a n d n =+-=-. 即数列{}n a 的通项公式为39n a n =-.当2n ≥时,()()()1211221122222n n n n n n n n b b b b b b b b -----=-+-++-+=++++=L L ,而12b =,故2n n b =,即数列{}n b 的通项公式为2nn b =.(Ⅱ)()()2162323122392n n n T n n -=-⨯-⨯++-⨯+-⨯L ,()()231262323122392n n n T n n +=-⨯-⨯++-⨯+-⨯L ,上述两式相减,得()21123232392nn n T n +-=-+⨯+⋯+⨯--⨯()()()11112324392243122n n n n n +++=-+⨯---⨯=---⨯得()1312224n n T n +=-⨯+.设()13122n n c n +=-⨯,显然当4n ≥时,0n c ≥,24n T ≥,且单调递增.而136c =-,248c =-,348c =-,故n T 的最小值为2324T T ==-.21.【浙江省金华十校2019届第二学期高考模拟】已知抛物线C :22(0)y px p =>的焦点是(1,0)F ,直线1l :1y k x =,2l :2y k x =分别与抛物线C 相交于点A 和点B ,过A ,B 的直线与圆O :224x y +=相切.(1)求直线AB 的方程(含1k 、2k );(2)若线段OA 与圆O 交于点M ,线段OB 与圆O 交于点N ,求MON S ∆的取值范围. 【答案】(1)1212()40k k x k k y -++=;(2)452] 【解析】(1)焦点是(1,0)F ,可得12p=,即2p =,设11(,)A x y ,22(,)B x y , 抛物线方程为24y x =,联立1y k x =,可得21144(,)A k k ,同理可得22244(,)B k k , 若AB 斜率存在,可得12121212AB y y k kk x x k k -==-+,AB 的方程为122112144()k k y x k k k k -=-+,化为1212()40k k x k k y -++=, AB 的斜率不存在时,也满足上面的方程,则直线AB 的方程为1212()40k k x k k y -++=;(2)过A ,B 的直线与圆O :224x y +=相切,可得2d r ===,化简为221212()()4k k k k ++=,即有1220k k -≤<,cos ||||OA OB AOB OA OB ⋅∠==⋅u u u r u u u r u u uru u u r =,由221212()()4k k kk ++=,可得cos AOB ∠=,22121212()44sin 52k k k k MON k k --+∠=-,设1252(5,9]t k k =-∈,则222121212()444sin 452MONk k k k S MON k k ∆--+=∠=⋅-2(5)2(5)444t t t----+=⋅218494918()184t t t t t-+-==-+≤-=,当7t =取等号,即121[2,0)k k =-∈-,所以max ()2MON S ∆=, 又2491618(5)55MON S ∆>-+=,即MON S ∆>,即有MON S ∆的取值范围为2]. 22.【2020届浙江省湖州市高三上学期期末】已知函数()()2log ln a f x x x x =+-,1a >. (1)求证:()f x 在()1,+∞上单调递增;(2)若关于x 的方程()1f x t -=在区间()0,∞+上有三个零点,求实数t 的值;(3)若对任意的112,,x x a a -⎡⎤∈⎣⎦,()()121f x f x e -≤-恒成立(e 为自然对数的底数),求实数a 的取值范围.【答案】(1)证明见解析,(2)2t =,(3)(]1,e【解析】 (1)()()2ln 1'21ln x f x xx a =⋅+-,∵1x >,∴()'0f x >,故()f x 在()1,+∞上单调递增.(2)()()()()2222ln ln ln 'ln x x a a f x x a +-=,令()()()222ln ln ln g x x x a a =+-,()()22'ln 0g x a x=+>,()10g =, 故当()0,1x ∈,()'0g x <,()1,x ∈+∞,()'0g x >,即()f x 在()0,1x ∈上单调递减;在()1,x ∈+∞上单调递增.()11f =, 若()()11f x t f x t -=⇔=±在区间()0,∞+上有三个零点,则11t -=,2t =. (3)()f x 在1,1x a -⎡⎤∈⎣⎦上单调递减;在(]1,x a ∈上单调递增.故()()min 11f x f ==,()()max 1max ,f x f f a a ⎧⎫⎛⎫=⎨⎬⎪⎝⎭⎩⎭, 令()()112ln h a f f a a a a a ⎛⎫=-=+-⎪⎝⎭,∴()0h a <, 故()max 1ln f x a a =+-,∴ln 1ln 1a a e a a e -≤-⇒-≤-, 因为1a >,设()ln a a a ϕ=-则1'()10a aϕ=->,故()ln a a a ϕ=-为增函数, 又()ln 1e e e e ϕ=-=-. ∴(]1,a e ∈.。
第6讲 利用函数性质解决抽象函数不等式(解析版)
7.【2018年普通高校招生全国卷一】已知函数 ,任取两个不相等的正数 , ,总有
,对于任意的 ,总有 ,若 有两个不同的零点,则正实数 的取值范围为__________.
3.已知函数 的定义域为 , , 是偶函数,任意 满足 ,则不等式 的解集为()
A. B.
C. D.
【来源】(全国1卷)2021届高三5月卫冕联考数学(理)试题
【答案】D
【分析】
由 是偶函数,得函数图像关于直线 对称,结合单调性求解不等式即可得到结果.
【详解】
因为 是偶函数,所以 的图像关于直线 对称,
【详解】
令 , ,
则 ,
因为 , ,所以 ,所以 在 上为单调递减函数,
当 时,由 可知 ,不满足 ;
当 时, ,所以 可化为 ,即 ,
因为 在 上为单调递减函数,所以 ,
所以不等式 的解集为 .
故选:A
【变式演练3】定义在非零实数集上的函数 满足 ,且 是区间 上的递增函数.
(1)求 的值;
(2)求证: ;
【详解】
令 ,则 可得
所以 是 上的奇函数,
,
当 时, ,所以 ,
是 上单调递增,
所以 是 上单调递增,
因为 ,
由 可得 即 ,
由 是 上单调递增,可得 解得: ,
所以不等式 的解集为 ,
故选:A.
【点睛】
关键点点睛:本题解题的关键点是:构造函数 ,根据已知条件判断 的奇偶性和单调性,利用单调性解不等式.
【答案】A
2020高三生物学考选择题必考点快练 必考点9
必考点9 人与动物生命调节1.(2018·浙江4月选考,11)下列关于人体内环境的叙述,错误的是( )A.心肌细胞内的CO2浓度低于其生活的内环境B.血管中的药物需经组织液进入肌细胞C.血浆蛋白进入组织液会引起组织肿胀D.内环境的成分中有葡萄糖和无机盐2.(2018·浙江4月选考,6)下列关于人体内性激素的叙述,错误的是( )A.睾酮促进卵细胞的发生B.雌激素促进女性皮下脂肪的积累C.雌激素增强输卵管和子宫的活动D.雄激素促进男性附属生殖器官的生长3.(2018·浙江4月选考,20)下列关于人体膝反射的叙述,错误的是( )A.若脊髓受损,刺激传出神经元后伸肌也会收缩B.刺激传入神经元,抑制性中间神经元不会兴奋C.膝反射的反射弧中,传出神经元的胞体位于脊髓中D.若膝盖下方的皮肤破损,刺激肌梭后也能发生膝反射4.(2018·浙江4月选考,16)取某实验小鼠皮肤片,分别移植到同种小鼠甲和切除胸腺的同种小鼠乙身上。
一段时间后,观测到该皮肤片在小鼠乙身上的存活时间比小鼠甲的长。
由此推断,对该皮肤片发生排斥反应(一般指移植物作为“非己”成分被免疫系统识别、破坏和清除的免疫反应)的主要细胞是( )A.中性粒细胞B.T淋巴细胞C.B淋巴细胞D.巨噬细胞5.(2018·宁波市3月新高考模拟)正常人体细胞与外部环境之间的部分物质交换如图所示,其中①②③④分别表示不同液体,下列叙述正确的是( )A.人体内环境包括①②③④B.血浆中的氧气进入图示细胞的途径是③→①→②C.③中含激素、血红蛋白、乳酸、CO2等物质D.通过排泄系统排出的液体废物中只含有尿素和尿酸6.(2018·鄞州中学3月选考模拟)下列不属于简单反射的是( )A.瞬目反射B.咀嚼反射C.直立反射D.吞咽反射7.(2018·浙江3月超级全能生A卷)如图表示的神经元为假单极神经元,a结构位于感受器,c结构位于神经节(近脊髓),e结构位于反射中枢。
2018年全国高考理科数学(全国一卷)试题及参考答案(2021年整理)
(完整word)2018年全国高考理科数学(全国一卷)试题及参考答案(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整word)2018年全国高考理科数学(全国一卷)试题及参考答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整word)2018年全国高考理科数学(全国一卷)试题及参考答案(word版可编辑修改)的全部内容。
2018年全国普通高等学校招生全国统一考试(全国一卷)理科数学一、选择题:(本题有12小题,每小题5分,共60分。
) 1、设z=,则∣z ∣=()A 。
0B.C.1D.2、已知集合A={x|x 2-x —2>0},则A =()A 、{x |-1〈x 〈2}B 、{x |—1≤x ≤2}C 、{x |x<-1}∪{x |x>2}D 、{x|x ≤-1}∪{x |x ≥2}3、某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是()A. 新农村建设后,种植收入减少B. 新农村建设后,其他收入增加了一倍以上C. 新农村建设后,养殖收入增加了一倍D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4、记S n 为等差数列{a n }的前n 项和,若3S 3=S 2+S 4,a 1=2,则a 5=()建设前经济收入构成比例 建设后经济收入构成比例A、—12B、—10C、10D、125、设函数f(x)=x3+(a—1)x2+ax。
