机械振动基础经典例题
《机械振动基础》期末复习试题5套含答案.doc

中南大学考试试卷2005 - 2006学年上学期时间门o分钟《机械振动基础》课程32学时1.5学分考试形式:闭卷专业年级:机械03级总分100分,占总评成绩70 %注:此页不作答题纸,请将答案写在答题纸上一、填空题(本题15分,每空1分)1>不同情况进行分类,振动(系统)大致可分成,()和非线性振动;确定振动和();()和强迫振动;周期振动和();()和离散系统。
2、在离散系统屮,弹性元件储存(),惯性元件储存(),()元件耗散能量。
3、周期运动的最简单形式是(),它是时间的单一()或()函数。
4、叠加原理是分析()的振动性质的基础。
5、系统的固有频率是系统()的频率,它只与系统的()和()有关,与系统受到的激励无关。
二、简答题(本题40分,每小题10分)1、简述机械振动的定义和系统发生振动的原因。
(10分)2、简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
(10分)3、共振具体指的是振动系统在什么状态下振动?简述其能量集聚过程?(20分)4、多自由系统振动的振型指的是什么?(10分)三、计算题(本题30分)图1 2、图2所示为3自由度无阻尼振动系统。
(1)列写系统自由振动微分方程式(含质量矩阵、刚度矩阵)(10分);(2)设k t[=k t2=k t3=k t4=k9 /, =/2/5 = /3 = 7,求系统固有频率(10 分)。
13 Kt3四、证明题(本题15分)对振动系统的任一位移{兀},证明Rayleigh商R(x)=⑷严⑷满足材 < 尺⑴ < 忒。
{x}\M\{x}这里,[K]和[M]分别是系统的刚度矩阵和质量矩阵,®和①,分别是系统的最低和最高固有频率。
(提示:用展开定理{x} = y{M} + y2{u2}+……+ y n{u n})3 •简述无阻尼单自由度系统共振的能量集聚过程。
(10 分) 4.简述线性多自由度系统动力响应分析方法。
(10 分)中南大学考试试卷2006 - 2007学年 上 学期 时间120分钟机械振动 课程 32 学时 2 学分 考试形式:闭卷专业年级: 机械04级 总分100分,占总评成绩 70%注:此页不作答题纸,请将答案写在答题纸上一、填空(15分,每空1分)1. 叠加原理在(A )中成立;在一定的条件下,可以用线性关系近似(B ) o2. 在振动系统中,弹性元件储存(C ),惯性元件储存(D ) , (E )元件耗散 能量。
【单元练】高中物理选修1第二章【机械振动】经典练习题(2)

一、选择题1.如图甲所示,在一条张紧的绳子上挂几个摆。
当a 摆振动的时候,其余各摆在a 摆的驱动下也逐步振动起来,不计空气阻力,达到稳定时,b 摆的振动图像如图乙。
下列说法正确的是( )A .稳定时b 摆的振幅最大B .稳定时b 摆的周期最大C .由图乙可以估算出b 摆的摆长D .由图乙可以估算出c 摆的摆长D 解析:DA .a 与c 的摆长接近,它们的固有频率接近,在a 摆的驱动下,稳定时c 摆的振幅最大,所以A 错误;B .bc 摆是在a 摆的驱动下振动起来的,则b 的周期等于外力周期,稳定时abc 摆的周期都相同,所以B 错误; CD .根据单摆的周期公式2l T g=解得224T gl π= 由图像可得a 摆周期,则可以算出a 摆的摆长,估算出c 摆的摆长,所以C 错误;D 正确; 故选D 。
2.下列说法中 不正确 的是( )A .将单摆从地球赤道移到南(北)极,振动频率将变大B .将单摆从地面移至距地面高度为地球半径的高度时,则其振动周期将变到原来的2倍C .将单摆移至绕地球运转的人造卫星中,其振动频率将不变D .在摆角很小的情况下,将单摆的振幅增大或减小,单摆的振动周期保持不变C 解析:CA 、将单摆从地球赤道移到南(北)极,重力加速度增加,根据2LT gπ=,振动的周期变小,故振动频率将变大,故A 正确;B 、重力等于万有引力,故:2Mm mg Gr =,解得:2GMg r =,将单摆从地面移至距地面高度为地球半径的高度时,r 增加为2倍,故g 减小为14;根据2T π=2倍,故B 正确; C 、将单摆移至绕地球运转的人造卫星中,处于完全失重状态,不能工作,故C 错误;D 、根据2T =,振动的周期与振幅无关;在摆角很小的情况下,将单摆的振幅增大或减小,单摆的振动周期保持不变,故D 正确. 【点睛】本题关键是根据单摆的周期公2T =和重力加速度公式2GM g r =分析,注意周期与振幅无关.3.关于简谐运动,下列说法正确的是( )A .做简谐运动物体所受的回复力方向不变,始终指向平衡位置B .在恒力的作用下,物体可能做简谐运动C .做简谐运动物体速度越来越大时,加速度一定越来越小D .做简谐运动物体的加速度方向始终与速度方向相反C 解析:CA .回复力是使做简谐运动的物体返回平衡位置并总指向平衡位置的力,所以物体在远离和靠近平衡位置时的方向不同,A 错误;B .物体做简谐运动中回复力满足F x κ=-即回复力大小与位移大小成正比,方向与位移方向相反,所以在恒力的作用下,物体不可能做简谐运动,B 错误;C .做简谐运动物体速度越来越大,说明物体向着平衡位置运动,物体受回复力越来越小,加速度一定越来越小,C 正确;D .做简谐运动物体的加速度方向始终指向平衡位置,速度方向与物体运动方向相同,物体做简谐运动过程中,加速度方向和速度方向有时相同,有时相反,D 错误。
机械振动基础作业(有答案-全版)
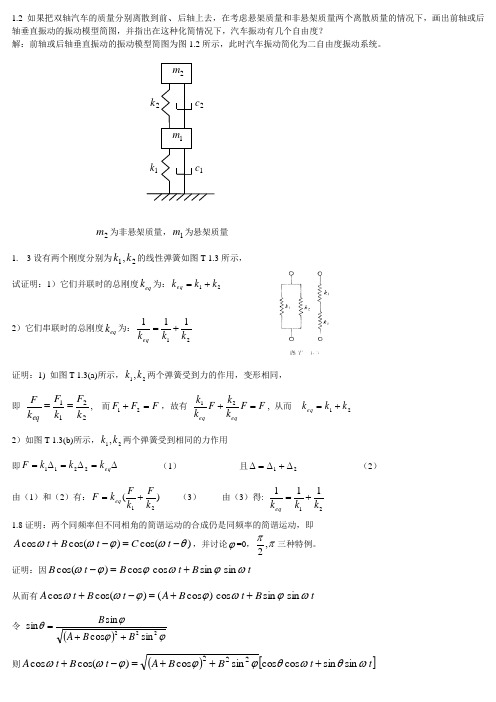
1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?解:前轴或后轴垂直振动的振动模型简图为图1.2所示,此时汽车振动简化为二自由度振动系统。
2m 为非悬架质量,1m 为悬架质量1. 3设有两个刚度分别为21,k k 的线性弹簧如图T-1.3所示, 试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 为:21111k k k eq +=证明:1) 如图T-1.3(a)所示,21,k k 两个弹簧受到力的作用,变形相同, 即2211k F k F k F eq ==, 而F F F =+21,故有 F F k kF k k eq eq =+21, 从而 21k k k eq +=2)如图T-1.3(b)所示,21,k k 两个弹簧受到相同的力作用 即∆=∆=∆=eq k k k F 2211 (1)且21∆+∆=∆ (2)由(1)和(2)有:)(21k Fk F k F eq += (3) 由(3)得:21111k k k eq += 1.8证明:两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动,即)cos()cos(cos θωϕωω-=-+t C t B t A ,并讨论ϕ=0,ππ,2三种特例。
证明:因t B t B t B ωϕωϕϕωsin sin cos cos )cos(+=-从而有t B t B A t B t A ωϕωϕϕωωsin sin cos )cos ()cos(cos ++=-+令 ()ϕϕϕθ222sin cos sin sin B B A B ++=则()[]t t B B A t B t A ωθωθϕϕϕωωsin sin cos cos sin cos )cos(cos 222+++=-+=())cos(sin cos 222θωϕϕ-++t B B A令C=()ϕϕ222sin cos B B A ++,则有 )cos()cos(cos θωϕωω-=-+t C t B t A当ϕ=0时,C=A+B ;当ϕ=2π时,22B A C +=,22BA arcsin +=B θ ;当ϕ=π时,B A -=C ,0=θ1.13汽车悬架减振器机械式常规性能试验台,其结构形式之一如图T-1.13所示。
机械振动习题及答案完整版.docx

1.1试举出振动设计'系统识别和环境预测的实例。
1.2如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?1.3设有两个刚度分别为心,心的线性弹簧如图T-1.3所示,试证明:1)它们并联时的总刚度k eq为:k eq = k x+ k22)它们串联时的总刚度匕满足:丿-畔+ 土keq & k2解:1)对系统施加力P,则两个弹簧的变形相同为X,但受力不同,分别为: P x = k x x<由力的平衡有:P = ^ + P,=(k1+k2)xp故等效刚度为:k eq^- = k1+k2x2)对系统施加力P,则两个弹簧的变形为:P%i=r 111,弹簧的总变形为:x = x}+x2= P(——I ---- )故等效刚度为:k =—Xk x k2k,2+ k、1 1=—l-------k、k21.4求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为心, 解:对系统施加扭矩T,则两轴的转角为:VTrx系统的总转角为:0 = G + g = Hy- + T-)褊k,i故等效刚度为:犒=二+二1.5两只减振器的粘性阻尼系数分别为q, C2,试计算总粘性阻尼系数"在两只减振器并联时,2)在两只减振器串联时。
解:1)对系统施加力P,则两个减振器的速度同为厂受力分别为:P{ - c x x<P2=C2X由力的平衡有:P=£ + E =(q+C2)Xp故等效刚度为:c eq=- = c]+c2X2)对系统施加力P,则两个减振器的速度为:p 1 1故等效刚度为:c eq=- = - + -1.6 一简谐运动,振幅为0. 5cm,周期为0.15s,求最大速度和加速度。
解:简谐运动的a>n= — = /5),振幅为5x10 3m ;= 5x10-cos(^_ 2/r即:—5x10'丽fsin(丽血/s)*610=(話讥。
第九章:机械振动典型例题

机械振动典型例题集锦第一节 简谐运动例题:一个质点做简谐振动,但他每次经过同一位置时,下列物理量一定相同的是:A .速度B .加速度C .动能D .动量出题目的:考查对简谐运动的基本特点的掌握情况解析:质点做简谐振动,他每次经过同一位置时,它的位移、加速度、速度大小相同,但方向不一定相同,所以它的动能相同而动量不相同。
所以B、C两选项正确。
评析:本题考查对简谐运动的基本特点的掌握情况,由于简谐运动是一个周期性的运动,所以它每经过同一位置时,有的物理量相同,有的物理量不同,因此,明确每个物理量的概念和简谐运动的特点才能做出正确判断。
例题: 已知弹簧振子的质量是2kg ,当它运动到平衡位置左侧2cm 时受到的回复力是4N ,求:当它运动到平衡位置右侧4cm 时,受到的回复力的大小和方向以及加速度的大小和方向.出题目的:本题考查对回复力及简谐运动公式的掌握.解:kx F -=,所以力1F 的大小11kx F =,由此可解得200=k N /m 则:8104200222=⨯⨯==-kx F N ,由于位移向右,回复力2F 方向向左.根据牛顿第二定律222m/s 428===m F a ,方向向左.例题:如图a 所示,将弹簧振子沿竖直方向悬挂起来,弹簧的劲度系数为k ,重物的质量为m .小球在平衡位置时,原先静止.在竖直方向将小球拉离平衡位置,松开后,小球就以平衡位置为中心上下振动.证明:小球做简谐运动.出题目的:考查简谐运动公式的运用.证明:设小球静止时,弹簧伸长为0x ,根据平衡条件mg kx =0 ①设向下为正方向,小球平衡位置为原点,小球振动过程中任一时刻,偏离平衡位置的位移为x (图b ),则在此时刻弹簧的伸长量为x x +0;小球受弹力)(0x x k f +=,方向向上.小球所受回复力为F[])(0x x k mg F +-+= ②将①代入②得kx F -=若0>x ,则0<F ,表示小球在平衡位置下方而合力方向向上;若0<x ,则0>F ,表示小球在平衡位置上方而合力方向向下.回复力满足kx F -=的条件,所以小球做简谐运动.例题: 如图所示,质量为m 的密度计,上部粗细均匀,横截面积为S ,漂浮在密度为ρ的液体中.现将密度计轻轻按下一段后放手,密度计上、下起伏.若不计液体的阻力,试证明密度计做的是简谐振动.出题目的:考查对简谐运动公式及特点的理解.解:简谐振动的重要特征是回复力大小与位移大小成正比,与位移方向相反.若密度计的振动也具有此特征,即可证明密度计做的是简谐振动.取向下为x 正方向,液面为平衡位置.密度计静止时,受重力mg 和浮力0F .mg F =0∴g V mg 0ρ= 0V ——密度计静止时浸没在液体中的体积.当密度计向下位移为x 时,所受浮力为:Sg x g V F ⋅+=ρρ0x gS mg Sg x g V mg F F ⋅-=+⋅⋅+-=+-=ρρρ)(0回当密度计向上位移为-x 时,所受浮力为:xSg g V F ρρ-='0)()(0x gS mg xSg g V mg F F -⋅-=+--=+'-='ρρρ回∴密度计所受回复力kx F -=回,其中gS k ρ=.密度计的振动是简谐振动。
高考复习——《机械振动》典型例题复习

九、机械振动1、机械振动 (1)平衡位置:物体振动时的中心位置,振动物体未开始振动时相对于参考系静止的位置,或沿振动方向所受合力等于零时所处的位置叫平衡位置。
(2)机械振动:物体在平衡位置附近所做的往复运动,叫做机械振动,通常简称为振动。
(3)振动特点:振动是一种往复运动,具有周期性和重复性 2、简谐运动(1)弹簧振子:一个轻质弹簧联接一个质点,弹簧的另一端固定,就构成了一个弹簧振子。
(2)振动形成的原因①回复力:振动物体受到的总能使振动物体回到平衡位置,且始终指向平衡位置的力,叫回复力。
振动物体的平衡位置也可说成是振动物体振动时受到的回复力为零的位置。
一、知识网络二、画龙点睛概念②形成原因:振子离开平衡位置后,回复力的作用使振了回到平衡位置,振子的惯性使振子离开平衡位置;系统的阻力足够小。
(4)简谐运动的力学特征①简谐运动:物体在跟偏离平衡位置的位移大小成正比,并且总指向平衡位置的回复力的作用下的振动,叫做简谐运动。
②动力学特征:回复力F与位移x之间的关系为F=-kx式中F为回复力,x为偏离平衡位置的位移,k是常数。
简谐运动的动力学特征是判断物体是否为简谐运动的依据。
③简谐运动的运动学特征a=-k m x加速度的大小与振动物体相对平衡位置的位移成正比,方向始终与位移方向相反,总指向平衡位置。
简谐运动加速度的大小和方向都在变化,是一种变加速运动。
简谐运动的运动学特征也可用来判断物体是否为简谐运动。
例题:试证明在竖直方向的弹簧振子做的也是简谐振运动。
证明:设O为振子的平衡位置,向下方向为正方向,此时弹簧形变量为x0,根据胡克定律得x0=mg/k当振子向下偏离平衡位置x时,回复力为F=mg-k(x+x0)则F=-kx所以此振动为简谐运动。
3、振幅、周期和频率⑴振幅①物理意义:振幅是描述振动强弱的物理量。
②定义:振动物体离开平衡位置的最大距离,叫做振动的振幅。
③单位:在国际单位制中,振幅的单位是米(m)。
机械振动基础

第4章 机械振动基础4-1 图示两个弹簧的刚性系数分别为k 1 = 5 kN/m ,k 2 = 3 kN/m 。
物块重量m = 4 kg 。
求物体自由振动的周期。
解:根据单自由度系统自由振动的固有频率公式 mk =n ω 解出周期 nπ2ω=T图(a )为两弹簧串联,其等效刚度 2121eq k k k k k +=所以 )(2121n k k m k k +=ω2121n)(π2π2k k k k m T +==ω代入数据得s 290.0300050003000)4(5000π2=⨯+=T图(b )为两弹簧串联(情况同a ) 所以 T = 0.290 s图(c )为两弹簧并联。
等效刚度 k eq = k 1 + k 2 所以 mk k 21n +=ω21nπ2π2k k mT +==ω代入数据得 T = 0.140 s图(d )为两弹簧并联(情况实质上同(c ))。
所以 T = 0.140 s4-3 如图所示,质量m = 200 kg 的重物在吊索上以等速度v = 5 m/s 下降。
当下降时,由于吊索嵌入滑轮的夹子内,吊索的上端突然被夹住,吊索的刚度系数k = 400 kN/m 。
如不计吊索的重量,求此后重物振动时吊索中的最大张力。
解:依题意,吊索夹住后,重物作单自由度自由振动,设振幅为A ,刚夹住时,吊索处于平衡位置,以平衡位置为零势能点,当重物达到最低点时其速度v = 0。
根据机械能守恒,系统在平衡位置的动能与最低点的势能相等。
即 T max = V max 其中 2max 2v m T = , 2max 21kA V =v km A =吊索中的最大张力 mk v mg kA mg F +=+=max 代入数据得 kN 7.461040020058.92003max =⋅⋅+⋅=F4-5 质量为m 的小车在斜面上自高度h 处滑下,而与缓冲器相碰,如图所示。
缓冲弹簧的刚性系数为k ,斜面倾角为θ。
机械振动试题(含答案)(1)

机械振动试题(含答案)(1)一、机械振动 选择题1.如图所示,在一根张紧的水平绳上,悬挂有 a 、b 、c 、d 、e 五个单摆,让a 摆略偏离平衡位置后无初速释放,在垂直纸面的平面内振动;接着其余各摆也开始振动,当振动稳定后,下列说法中正确的有( )A .各摆的振动周期与a 摆相同B .各摆的振动周期不同,c 摆的周期最长C .各摆均做自由振动D .各摆的振幅大小不同,c 摆的振幅最大2.如图所示,质量为m 的物块放置在质量为M 的木板上,木板与弹簧相连,它们一起在光滑水平面上做简谐振动,周期为T ,振动过程中m 、M 之间无相对运动,设弹簧的劲度系数为k 、物块和木板之间滑动摩擦因数为μ,A .若t 时刻和()t t +∆时刻物块受到的摩擦力大小相等,方向相反,则t ∆一定等于2T 的整数倍 B .若2T t ∆=,则在t 时刻和()t t +∆时刻弹簧的长度一定相同 C .研究木板的运动,弹簧弹力充当了木板做简谐运动的回复力 D .当整体离开平衡位置的位移为x 时,物块与木板间的摩擦力大小等于m kx m M+ 3.用图甲所示的装置可以测量物体做匀加速直线运动的加速度,用装有墨水的小漏斗和细线做成单摆,水平纸带中央的虚线在单摆平衡位置的正下方。
物体带动纸带一起向左运动时,让单摆小幅度前后摆动,于是在纸带上留下如图所示的径迹。
图乙为某次实验中获得的纸带的俯视图,径迹与中央虚线的交点分别为A 、B 、C 、D ,用刻度尺测出A 、B 间的距离为x 1;C 、D 间的距离为x 2。
已知单摆的摆长为L ,重力加速度为g ,则此次实验中测得的物体的加速度为( )A .212()x x g L π-B .212()2x x g L π-C .212()4x x g L π-D .212()8x x g Lπ- 4.如图所示,弹簧下面挂一质量为m 的物体,物体在竖直方向上做振幅为A 的简谐运动,当物体振动到最高点时,弹簧正好处于原长,弹簧在弹性限度内,则物体在振动过程中A .弹簧的弹性势能和物体动能总和不变B .物体在最低点时的加速度大小应为2gC .物体在最低点时所受弹簧的弹力大小应为mgD .弹簧的最大弹性势能等于2mgA5.如图所示是扬声器纸盆中心做简谐运动的振动图象,下列判断正确的是A .t =2×10-3s 时刻纸盆中心的速度最大B .t =3×10-3s 时刻纸盆中心的加速度最大C .在0〜l×10-3s 之间纸盆中心的速度方向与加速度方向相同D .纸盆中心做简谐运动的方程为x =1.5×10-4cos50πt (m )6.在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议,可行的是( ) A .适当加长摆线B .质量相同,体积不同的摆球,应选用体积较大的C .单摆偏离平衡位置的角度要适当大一些D .当单摆经过平衡位置时开始计时,经过一次全振动后停止计时,用此时间间隔作为单摆振动的周期7.图(甲)所示为以O 点为平衡位置、在A 、B 两点间做简谐运动的弹簧振子,图(乙)为这个弹簧振子的振动图象,由图可知下列说法中正确的是( )A.在t=0.2s时,弹簧振子可能运动到B位置B.在t=0.1s与t=0.3s两个时刻,弹簧振子的速度相同C.从t=0到t=0.2s的时间内,弹簧振子的动能持续地增加D.在t=0.2s与t=0.6s两个时刻,弹簧振子的加速度相同8.悬挂在竖直方向上的弹簧振子,周期T=2s,从最低点位置向上运动时刻开始计时,在一个周期内的振动图象如图所示,关于这个图象,下列哪些说法是正确的是()A.t=1.25s时,振子的加速度为正,速度也为正B.t=1.7s时,振子的加速度为负,速度也为负C.t=1.0s时,振子的速度为零,加速度为负的最大值D.t=1.5s时,振子的速度为零,加速度为负的最大值9.如图所示,一端固定于天花板上的一轻弹簧,下端悬挂了质量均为m的A、B两物体,平衡后剪断A、B间细线,此后A将做简谐运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m1 1.0 m2
因此得到空载时的阻尼比为:
满载和空载时的频率比: r1
r2
m 1 1.87 n1 k m2 0.93 n 2 k
满载时阻尼比 1 0.5
空载时阻尼比 2 1.0 满载时频率比 r1 1.87 空载时频率比 r2 0.93
1 2 2 1 ka mgl mgl 2 2 2 1 (ka 2 mgl ) 2 mgl 2
d T U 0 dt
2ml 2 2 (ka 2 mgl ) 0 2ml 2 2(ka 2 mgl ) 0
ka 2 mgl n ml 2
系统最大动能
Tmax
m
1 ) 2 1 mA2 2 c 2 m(c n 2 2
1 1 2 U1 k1 ( max a ) k2 ( max b) 2 最大弹性势能 2 2 1 1 2 U 2 mg (1 cos max )c mgc max mgcA2 最大重力势能 2 2
解: (1)系统的固有频率
共振时
1 X 2 F / k
1 n 2 10 0.20
有
c
F 25 62.66 2 X 1.27 10 10
c 62.66 0.51 2mn 2 1.95 10
(2)振动频率为 f = 4Hz , 频率比 r f 4 0.8
解法2: 广义坐标θ,零平衡位置2 动能 势能
1 2 1 2 2 T J ml 2 2
11 2 U 2 k a mgl cos 22
m k/2
k/2
l
a
零平衡位置2
1 2 2 ka mgl 1 2sin 2 2 2
n 1
4 F0
1 n sin nt n 1,3,5
n t1
x0e
1 2
d
x1 x(t1 ) x0e
n t1
x0e
1 2
由题设质量块最大位移为初始位移的 10%,可知
x1 e x0
1 2
10%
解得:
0.59
例: 小球质量 m , 刚杆质量不计 求:
a b l c k m
T
t
求系统响应
解:
F0 a0 F (t ) (an cos nt bn sin nt ) 2 n 1 0
bn sin nt
n 1
F (t )
F0
T /2
T
t
2 T =0 a0 T 0 F (t )dt 2 T an 0 F (t ) cos ntdt T 2 T bn T 0 F (t ) sin ntdt
3)传到地基上的力幅 :
FT TF F 0.149 1470 219 N
例:弹簧-质量系统受到周期为T 的方波激励, 系统固有频率为ωn
F (t )
T 0t F0 , 2 F (t ) F , T t T 0 2
F0
0 T /2
F0
f A
动力学方程
mx k ( x x f ) 0
mx kx (kbd / a ) sin t
X
振幅:
kbd / a 1 bd 1 k 1 r2 a 1 r2
例题:机器安装在弹性支承上 ,已测得固有频率 fn=12.5Hz ,阻尼比 =0.15 ,参与振动的质量是 880kg ,机器转速 n=2400r/min ,不平衡力的幅值 1470N ; 求:1)机器振幅 2)主动隔振系数 3)传到地基 上的力幅 2 n 1 解:1)频率比: r 60 2 f 3.2 n n
l =5 m
a
z
求: 拖车在满载和空载时的振幅比
解:汽车行驶的路程可表示为:
2 v x f a sin t 因此: l
z vt
m
x
0 k/2 l =5 m
k/2
c
路面的激励频率:
2 v 34.9 rad / s l
x
f
x
f
a
z
l
有 c 2 km
c、k 为常数,因此 与 m 成反比
例题:偏心质量系统,共振时 测得最大振幅为0.1m,由自由 衰减振动测得阻尼系数为
m 10% 0.05 ,假定 M
k 2
c e m
t
x
k 2
求:
(1)偏心距 e,
me 2 sin t
M
x
(2)若要使系统共振时振幅为
0.01m,系统的总质量需要增加多少?
k
c
解:(1)共振时最大振幅
n
fn 1/ 20
无阻尼时系统振幅
F 1 X k 1 r2
X F 1 k (1 r 2 ) 2 (2 r ) 2
有阻尼时系统振幅
无阻尼与有阻尼系统振幅比为
X 2 r 2 2 0.51 0.8 2 1 ( ) 1 ( ) 2.48 2 2 X 1 r 1 0.8
k mn 2 880 (2 12.5) 2 5.43 106 N 弹性支承的刚度:
F 1 X 0.0291(mm) 机器振动的振幅 : k 2 2 2 (1 r ) (2 r )
2)主动隔振系数 :
1 (2 r ) 2 TF 0.149 2 2 2 (1 r ) (2 r )
因此满载和空载时的振幅比:
X1 0.6 X2
例题2:已知梁截面惯性矩I, B A m 弹性模量E,梁质量不计, yA 支座A产生微小竖直振动 b a y A d sin t ,支座B不动 求:质量m的稳态振动振幅 解:在质量m作用下,由材料力学可求出静挠度δ n g / 固有频率: xf 是因 yA 的运动而产生的质量m处的运动 x (b / a ) y (bd / a ) sin t
由
Tmax U max
得
b k2
1 1 1 1 2 2 2 2 2 2 2 mA n c k1 A a k2 A b mgcA2 2 2 2 2
θ
整理得
k1
a c θ
k1a 2 k2b 2 mgc n mc 2
m
例:在图示系统中,弹簧长l,其质量ms ,质量块m, 求弹簧的等效质量及系统的固有频率。
n
平衡位置
P m k x0
0
求导
n 2 x0 t x(t ) e sin d t d
n
x c
设在时刻 nt21x0 t 质量越过平衡位置到达最大位移,这时
x(t1 )
速度为:
d
e
n1
sin d t1 0
t1
x1 x(t1 ) x0e
a0在一个周期内总面积为0 ;
=0
区间[0,T]内,F(t)关于T/2为反
对称,而cosnωt关于T/2对称。
F (t ) bn sin nt
n 1
F (t )
F0
0 T /2
2 bn F (t ) sin ntdt T 0
T
F0
T 4
T
t
区间
内,F(t)关于 对称, T sin nt 4 而 n 取偶数时, 关于 反对称; T 3T 区间 内,F(t) 关于 对称, 3T sin nt 4 而 n 取偶数时, 关于 反对称; 因此 bn=0, n=2,4,6 …
2 ,T
4
T 0, 2
当 n 取奇数时
8 2 T bn F (t ) sin ntdt T 0 T
T 4 0
4F0 F0 sin ntdt n
n 1,3,5
于是,周期性激励F(t)可写为:
F (t ) bn sin nt
a
l
势能
1 2 2 ka mgl 1 1 2sin 2 2 2
1 (ka 2 2 mgl 2 ) 2
1 (ka 2 mgl ) 2 2
Tmax U max
max
n max
ka 2 mgl n ml 2
例1:如图所示是一个倒置的摆, 摆球质量 m,刚杆质量忽略不计, 每个弹簧的刚度是k/2, 求:倒摆作微幅振动时的 固有频率 可以有几种解法?
m k/2 k/2 a l
解法1:
m k/2
零平衡位置1
k/2
广义坐标θ,零平衡位置1
动能
1 2 1 2 2 T J ml 2 2
11 2 U 2 k a mgl 1 cos 22
ca 2 m 1 2mlb k
2bl ccr 2 mk a
例题:一个质量为1.95kg的物体在粘性阻尼介质中 作强迫振动,激励力为 F 25sin(2 ft )N, (1)测得系统共振时的振幅为1.27cm,周期为0.20s, 求系统的阻尼比及阻尼系数;(2)如果 f = 4Hz,无 阻尼时振幅是有阻尼时振幅的多少倍
无阻尼固有频率:
kb 2 b k n 2 ml l m
c a
k b
m
ml
ca 2n 2 ml
2
ca 2 ca 2 m 2 2ml n 2mlb k
阻尼固有频率:
d n
1 1 4kmb 2l 2 c 2 a 4 2ml 2
