第二章 (4)卷积积分的性质
第二章 信号与系统的时域分析

二 卷积积分(The convolution integral) 若 (t ) h(t ) 则 (t ) h(t ) = h (t )
x t x h t
x(t ) x( ) (t )d y(t ) x( )h (t )d
则 y(t ) ak yk (t )
k
4
信号与系统的时域分析:
一般的信号都可以表示为延迟冲激的线性组合。
结合系统的叠加性和时不变性,就能够用LTI的单位
冲激响应来完全表征任何一个LTI系统的特性。这样
一种表示在离散情况下称为卷积和;在连续时间情
况下称为卷积积分。
5
分析方法:
对信号分解可在时域进行,也可在频域或变换域 进行,相应地产生了对LTI系统的时域分析法、频 域分析法和变换域分析法。
h( n n kk n h ) uu (n k )k
1
1
k
0
...
0
k
n
12
运算过程:
k k) ,再随参变量 为 h(
点值累加,得到
将一个信号 xk 不动,另一个信号反转后成为
下,将 xk 与 hn k 对应点相乘,再把乘积的各
n
移位.在每个 n 值的情况
x( [ n] y x x[ (n n] )* [ (n) h2 (n n)] x ) y( n n) (h h1 ) 1 n h2 h (n ) h( n) h2 x(t ) 11 y(t ) x(t ) [h1 (t ) h2 (t )] h1 (t ) h2 (t )
0
16
对一般信号 x(t ) ,可以分成很多 宽度的区段, 用一个阶梯信号 x (t ) 近似表示 x(t ) .当 0 时,
《信号与系统》第二章总结

它确定系统完全响应的系数:
d + r (0 ), r ' (0 ), r ' ' (0 ), r ' ' ' (0 ) L, n −1 r (0 ) dt
+ + + +
n −1
r (t ) = rh (t ) + rp (t ) = ∑ Ai eα it + rp (t )
i =1
n
冲激函数匹配法
阶跃响应
产生 阶跃响应g (t ):系统激励u (t ) 零状态响应 →
g (t )满足微分方程为 d n g (t ) d n −1 g (t ) dg (t ) C0 + C1 + L + Cn −1 + Cn g (t ) n n −1 dt dt dt d m u (t ) d m −1u (t ) du (t ) = E0 dt m + E1 dt m −1 + L + Em −1 dt + Emu (t ) (k ) g (0− ) = 0
(5)积分性: ∫
t
−∞
[ f1(τ ) ∗ f2 (τ )]dτ = f1(t) ∗ ∫−∞ f2 (τ )dτ
t
(适于多重积分)
= ∫ f1 (τ )dτ ∗ f2 (t )
−∞
t
(6)微积分性:设 f (t ) = f1 (t ) ∗ f 2 (t ) 则f
(i )
(t ) = f
( j) 1
(t ) ∗ f 2
(i − j )
(t )
(7)冲激性: f (t ) ∗ δ (t ) = f (t ) f (t ) ∗ δ (t − t0 ) = f (t − t0 )
卷积的数学性质

卷积的数学性质
卷积是一种数学操作,可以用来将两个函数的值连接在一起,以及在号处理和图像处理领域中实现息提取和特征提取的有效技术。
卷积可以被认为是离散滤波器和泛函分析的基础。
卷积运算可以被定义为两个函数f(x)和g(x)的积分运算,其中f(x)是输入函数,g(x)是卷积核。
卷积的计算过程
可以分为两步:第一步,把f(x)乘以g(x);第二步,对
乘积结果进行积分计算。
卷积操作具有许多有用的性质,尤其是在处理号和图像时。
其中最重要的性质之一是卷积的平移不变性,即卷积结果不受输入函数的位移影响。
卷积运算也具有反卷积性质,即可以通过反卷积操作将输出函数变为输入函数。
此外,卷积运算也具有旋转不变性,即卷积结果不受输入函数的旋转影响。
此外,卷积操作还有一些其他性质,例如可以用于检测图像中的特定形状,可以用于提取图像中的特定特征,可以用于探测图像中的边缘等。
卷积操作在现代号处理和图像处理中起着重要作用,例如在计算机视觉领域,可以用卷积操作提取视觉特征,以实现更好的识别和分类效果;在语音处理领域,可以用卷积操作提取语音特征,以实现更好的识别效果;在机器研究领域,可以用卷积操作提取特征,以实现更好的研究效果。
因此,卷积操作在处理号和图像时起着重要作用,具有许多有用的数学性质,可以有效地提取息和特征,并在多个领域实现有效的应用。
信号与系统王明泉版本~第二章习题解答
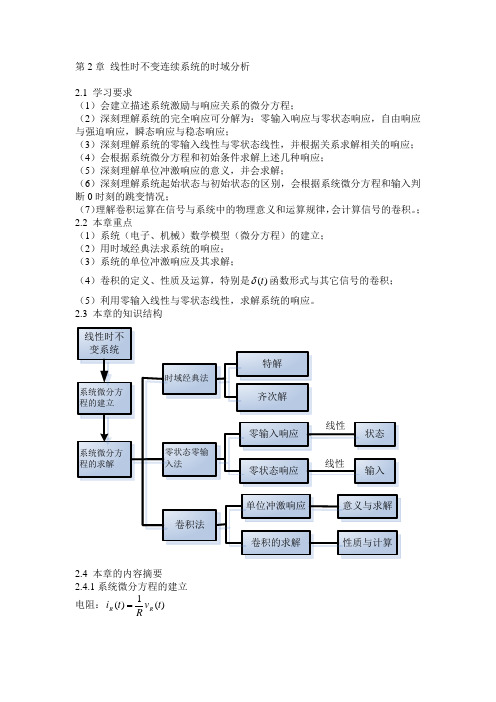
第2章 线性时不变连续系统的时域分析2.1 学习要求(1)会建立描述系统激励与响应关系的微分方程;(2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应,瞬态响应与稳态响应;(3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应; (4)会根据系统微分方程和初始条件求解上述几种响应; (5)深刻理解单位冲激响应的意义,并会求解;(6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断0时刻的跳变情况; (7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。
; 2.2 本章重点(1)系统(电子、机械)数学模型(微分方程)的建立; (2)用时域经典法求系统的响应; (3)系统的单位冲激响应及其求解;(4)卷积的定义、性质及运算,特别是()t δ函数形式与其它信号的卷积; (5)利用零输入线性与零状态线性,求解系统的响应。
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻:)(1)(t v Rt i R R =电感:dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容:dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。
齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时,如1λ有k 重根,则响应于1λ的重根部分将有k 项,形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根,即bi a +=2,1λ,则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根,即共有m 重ib a ±=2,1λ的复根,则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。
2.4 卷积积分的性质

(t ) f (t ) d t f (0)
证: f (t )* (t ) (t )* f (t ) ( ) f (t ) d f (t )
f t t t0 f t t0
两种运算的不同之处仅在于,卷积运算需将 f2 进行反折
为 f 2 ,而相关运算不需反折,仍为 f2 。其他的移位、相乘 和积分的运算方法相同。
通信与信息工程学院基础教学部
小结: 求卷积是本章的重点与难点。
• 求解卷积的方法可归纳为: • (1)利用定义式,直接进行积分。对于容易求积分的函数比 较有效。如指数函数,多项式函数等。 • (2)图解法。特别适用于求某时刻点上的卷积值。 • (3)利用性质。比较灵活。 三者常常结合起来使用。
( ) f (t ) f (t ) ( ) d f (t )
f t
n
t f
n
t
3. f t t f ( ) (t ) d f ( ) d 对函数积分
t t t t
通信与信息工程学院基础教d n f1 (t ) d n f 2 (t ) dn f (t ) * f 2 (t ) * f 2 (t ) f1 (t ) * 1. n 1 n dt dt d tn dn f1 t f 2 t 证: n f1 (t )* f 2 (t ) n t dt n f2 t t f t 1
t 0
(t ) (1 e t ) (t )
积分变换第4讲卷积定理与相关函数

解 :F(si n w 0 t
• u(t )) F(e iw0t
e iw0t 2i
• u(t))
1 {F(e iw0t • u(t )) F (e iw0t • u(t ))}
2i
1{1 2i iw
d(w)} |www0
1{1 2i iw
d(w)} |www0
例4 利用傅氏变换的性质, 求d(tt0),
ejw0t ,以及tu(t )的傅氏变换 解:因F (d (t)) 1,由位移性质得
F (d (t t0)) e jt0w F (d (t)) e jt0w 由 F (1) 2d (w),得
F (ejw0t ) 2d (w w0)
w0t
•
e t u(t ))
F
( eiw0t
eiw0t 2
•
e t u(t ))
1 {F (eiw0t • e tu(t)) F (eiw0t • u(t))}
2
1 2
{ iw
1
}
|w
w
w0
1 2
{ iw
1
}
|w
w
w0
1 2
{ i
w
1 w0
2n
t
Dt
n
则g(t)
f
(t
)
1
Dt
e
j
2n
t
Dt
n
G(w)
1
Dt
F (w nDw)
n
(Dw
2 Dt
)
33
信号与系统笔记

信号与系统第一章1。
1 连续时间与离散时间信号确知信号可以表示成一个或几个自变量的函数连续时间信号在[t1,t2]区间的能量定义为:连续时间信号在[t1,t2]区间的平均功率定义为:离散时间信号在[n1,n2]区间的能量定义为离散时间信号在[n1,n2]区间的平均功率为在无限区间上也可以定义信号的总能量:连续时间情况下:离散时间情况下:在无限区间内的平均功率可定义为: 21lim 2()TTT P dtTx t ∞-→∞=⎰能量信号——信号具有有限的总能量,即:功率信号—-信号有无限的总能量,但平均功率有限。
即:信号的总能量和平均功率都是无限的。
即:如果信号是周期信号,则或这种信号也称为功率信号,通常用它的平均功率来表征或或如果信号是非周期的,且能量有限则称为能量信号。
1.2 自变量的变换1.时移变换当时,信号向右平移时,信号向左平移当时,信号向右平移 时,信号向左平移,0E P ∞∞<∞=,E P ∞∞=∞=∞2。
反转变换信号以t=0为轴呈镜像对称。
与连续时间的情况相同。
3. 尺度变换时,是将在时间上压缩a倍,时,是将在时间上扩展1/a倍。
由于离散时间信号的自变量只能取整数值,因而尺度变换只对连续时间信号而言。
周期信号与非周期信号:周期信号:满足此关系的正实数(正整数)中最小的一个,称为信号的基波周期()。
可视为周期信号,但它的基波周期没有确定的定义。
可以视为周期信号,其基波周期。
奇信号与偶信号:对实信号而言:如果有和则称该信号是偶信号。
(镜像偶对称)如果有和则称该信号为奇信号。
(镜像奇对称)对复信号而言:如果有和则称该信号为共轭偶信号.如果有和则称为共轭奇信号。
任何信号都能分解成一个偶信号与一个奇信号之和。
对实信号有:其中其中对复信号有:其中:其中:1。
3 复指数信号与正弦信号一. 连续时间复指数信号与正弦信号其中C, a 为复数1. 实指数信号:C,a 为实数呈单调指数上升呈单调指数下降。
信号与系统 卷积积分的性质

信号与系统
d x t dt
h d
t
2
1
1 0
2
c
1
t
0
4
t
d
dxt t h d 15 dt 8
t
9 8
2
dxt t h d dt
3
1 0
2
2
6
1 0
2 3
6
t
f
e
信号与系统
t t t
[ 1 d ]u (t 1) [ 1 d ]u (t 2)
1 2
t
t
(t 1)u (t 1) (t 2)u (t 2)
(t 1)[u (t 1) u (t 2)] 3u (t 2) 0 t 1 3
0 t a 1 e d 1 e at 0 a
f t
1
1 d ]u(t ) 1 e at u t a
t 0
f d
t 0
t
e at
1 a
0
a
t
0
b
t
信号与系统
作业 13-4-16
t
y( )d f (t ) h( )d h(t ) f ( )d
t
y(t)的一重积分
y ( 1) (t ) f (t ) h( 1) (t ) f ( 1) (t ) h(t )
推广:
y ( m) (t ) f (t ) h( m) (t ) f ( m) (t ) h(t )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f 1 (t )
f 2 (t )
2
1
0
2
0 1
1
2 3
t
1
3
t
解法一: 解法一:图示法
f 1 (τ
t <1 ,
)
f (t ) = 0
2
0
1
2 3
τ
f 2 (t τ
t2
)
1
t 0
1
τ
解法一: 解法一:图示法
f 1 (τ
t <1 ,
)
t
f (t ) = 0
1< t < 2 ,
f (t ) = ∫ 2dτ = 2(t 1)
(2) e ε(t + 3) ε(t 5) 2t e ε (t + 3) ε (t 5) ∞ 2τ = ∫ e ε (τ + 3) ε (t τ 5)dτ ∞
2t
=∫t 53e2τ1 2(t 5) 6 e = e 2 6 1 2( t 2) = e 1 e 2
[
1 2τ dτ = e 2
' ∞ ∞
上式称为杜阿密尔积分. 上式称为杜阿密尔积分. 杜阿密尔积分 其物理含义为: 其物理含义为:LTI系统的零状态响应等于激励的 系统的零状态响应等于激励的
f ' (t )与系统的阶跃响应 g(t )的卷积积分. 的卷积积分. 导数
例2.4-4 求图示函数 f1(t ) 与 f2 (t ) 的卷积 f (t ) .
若f (t ) = f1(t ) f2(t ),则 f1(t t1 ) f2(t t2 ) = f1(t t2 ) f2 (t t1 ) = f (t t1 t2 )
推广4 推广
推广4 推广
若f (t ) = f1(t ) f2(t ),则 f1(t t1 ) f2(t t2 ) = f1(t t2 ) f2 (t t1 ) = f (t t1 t2
积分: 积分:
f
( 1)
(t ) = f
( 1) 1
(t ) f2 (t ) = f1(t ) f
( 1) 2
( 1) 2
(t )
推论: f 推论:(t ) = f (t ) f
(1) 1
(t ) = f (t )
( 1) 1
(t ) f (t )
(1) 2
f (t ) = f
(i )
( j) 1
f (t )
h (t ) 2
h (t ) 1
y f (t )
f (t )
h(t ) = h (t ) h2 (t ) 1
y f (t )
∵[ f (t ) h (t )] h2(t ) = f (t ) [h (t ) h2(t )] 1 1 [ f (t ) h2(t )] h (t ) = f (t ) [h2(t ) h (t )] 1 1 = f (t ) [h (t ) h2(t )] 1
(t ) f
(i j ) 2
LTI系统的零状态响应等于激励与系统冲激响应的卷积 系统的零状态响应等于激励与系统冲激响应的卷积 积分,利用上面的结论可得: 积分,利用上面的结论可得:
y f (t ) = f (t ) h(t ) = f (1) (t ) h(1) (t ) = f (1) (t ) g(t ) = ∫ f (τ )g(t τ )dτ
复习
1,卷积的图解法求解 2,卷积的解析法求解
第四节 卷积积分的性质 一,卷积的代数运算
交换律 f1(t ) f2 (t ) = f2 (t ) f1(t )
下面我们来看一道例题. 下面我们来看一道例题.
2 例 .4 1 设 1(t ) = eαtε (t ),f2 (t ) = ε (t ),分别求: : f f1(t ) f2 (t )和f2 (t ) f1(t ).
Def
f
( 1)
(t ) =
Def
∫
t
∞
f ( x)dx
其中: 其中: f
( 1)
( ∞) = 0
若
f (t ) = f1(t ) f2 (t ) = f2 (t ) f1(t )
f (t ) = f (t ) f2 (t ) = f1(t ) f (t )
(1) (1) 1 (1) 2
则其导数: 则其导数:
证明: 证明: f1(t t1 ) f2(t t2 ) =
令τ t1 = x则
∞
∫∞ f1(τ t1) f2(t τ t2 )dτ
∞
= f (t t1 t2 )
同理: 同理:
原式 = ∫ f1( x) f2 (t x t1 t2 )dx
∞
f1(t t2 ) f2(t t1) = f (t t1 t2 )
∞ ∞ ∞ ∞ t
f1(τ ) f2(t τ )dτ
= ∫ eατε (τ ) ε (t τ )dτ =∫ e
0 ατ
dτ =
1
f2(t ) f1(t ) = ∫
∞ ∞
α
(1 eαt )ε (t )
∞ ∞ t
f2(τ ) f1(t τ )dτ
α(t τ )
= ∫ ε (τ ) e =∫ e
结论:并联系统的冲激响应, 结论:并联系统的冲激响应,等于组成并联系 统的各个子系统冲激响应之和. 统的各个子系统冲激响应之和.
h2(t )
h (t ) + h2 (t ) 1
h(t ) =
y f (t )
结合律及其应用: 结合律及其应用:
[ f1(t ) f2 (t )] f3 (t ) = f1(t ) [ f2 (t ) f3 (t )] f (t ) y f (t ) h (t ) h (t ) 2 1
f 2 (t t 2 )
f (t t1 t 2 )
0
t1
t
0
t2
t
0
t1+ t2
t
f1 (t t 2 )
f 2 (t t1 )
f (t t1 t 2 )
0
t2
t
0 t1
t
0
t1+ t2
t
图 2.4-6
计算下列卷积积分: 例2.4-2 计算下列卷积积分:
(1) ε(t + 3) ε(t 5)
实际上利用
推广4 推广
若f (t ) = f1(t ) f2(t ),则 f1(t t1 ) f2(t t2 ) = f1(t t2 ) f2 (t t1 ) = f (t t1 t2 )
∵ε (t ) ε (t ) = tε (t )
∴ε (t + 3) ε (t 5) = (t 2)ε (t 2)
推广1 推广
f (t ) δ (t t1 ) = δ (t t1 ) f (t ) = f (t t1 ) 若 f (t ) = δ (t t1 ) 得:
推广2 推广 推广3 推广
δ ( t t1 ) δ ( t t 2 ) = δ ( t t1 t 2 )
f (t t1 )δ (t t2 ) = f (t t2 )δ (t t1 ) = f (t t1 t2 )
f (t ) = fo (t ) δT (t ) ∞ = fo (t ) ∑δ (t mT ) m=∞
-2T -T 0 T 2T
t
(a)
f 0 (t )
=
m=∞
∑[ f (t ) δ (t mT )]
o
∞
=
m=∞
∑ f (t mT )
o
∞
(b) f 0 (t ) δ T (t )
T 0 T
0 α(t τ )
ε (t τ )dτ
(1 eαt )ε (t )
dτ =
1
α
分配律的应用
f1(t ) [ f2 (t ) + f3 (t )] = f1(t ) f2 (t ) + f1(t ) f3 (t )
f (t )
h1(t )
+ +
∑
y f (t ) f (t )
∵ f (t ) h (t ) + f (t ) h2(t ) = f (t ) [h (t ) + h2(t )] 1 1
2t
=e e
6
6 2( t +3)
ε (t + 3) ε (t 5)
1 2( t 2) = e 1 e ε (t 2) 2
[
]
下页图( 画出了周期为 画出了周期为T的周期性单位冲激 例2.4-3 下页图(a)画出了周期为 的周期性单位冲激 函数序列,可称为梳状函数, 函数序列,可称为梳状函数,它可用符号 它可写为: 它可写为:
t
图 2.4-4函数与冲积函数的卷积 函数与冲积函数的卷积
f (t t1 )
δ (t t 2 )
f (t t1 t 2 )
0
t1
t
0
t2
t
0
t1+ t2
t
f (t t 2 )
δ (t t1 )
f (t t1 t 2 )
0
t2
t
0
t1
t
0
t1+ t2
t
图 2.4-5
f1 (t t1 )
结论:串联系统的冲激响应, 结论:串联系统的冲激响应,等于组成串联系统 的各个子系统的冲激响应的卷积. 的各个子系统的冲激响应的卷积.
二,函数与冲激函数的卷积
f (t ) δ (t ) = δ (t ) f (t ) = f (t )
f (t ) δ (t ) = δ (t ) f (t ) = ∫ δ (τ ) f (t τ )dτ = f (t )
