电力系统负荷预测报告材料

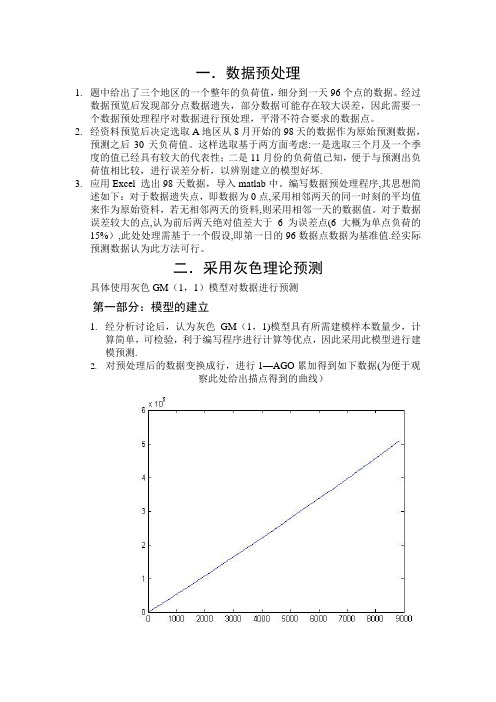
一．数据预处理1.题中给出了三个地区的一个整年的负荷值，细分到一天96个点的数据。

经过数据预览后发现部分点数据遗失，部分数据可能存在较大误差，因此需要一个数据预处理程序对数据进行预处理，平滑不符合要求的数据点。

2.经资料预览后决定选取A地区从8月开始的98天的数据作为原始预测数据，预测之后30天负荷值。

这样选取基于两方面考虑：一是选取三个月及一个季度的值已经具有较大的代表性；二是11月份的负荷值已知，便于与预测出负荷值相比较，进行误差分析，以辨别建立的模型好坏。

3.应用Excel 选出98天数据，导入matlab中。

编写数据预处理程序，其思想简述如下：对于数据遗失点，即数据为0点，采用相邻两天的同一时刻的平均值来作为原始资料，若无相邻两天的资料，则采用相邻一天的数据值。

对于数据误差较大的点，认为前后两天绝对值差大于6为误差点（6大概为单点负荷的15%），此处处理需基于一个假设，即第一日的96数据点数据为基准值。

经实际预测数据认为此方法可行。

二．采用灰色理论预测具体使用灰色GM（1，1）模型对数据进行预测第一部分：模型的建立1.经分析讨论后，认为灰色GM（1，1）模型具有所需建模样本数量少，计算简单，可检验，利于编写程序进行计算等优点，因此采用此模型进行建模预测。

2.对预处理后的数据变换成行，进行1-AGO累加得到如下数据（为便于观察此处给出描点得到的曲线）3.依据灰色预测步骤建立累加矩阵B 及常数相向量Y 。

4.利用最小二乘法求出灰系数。

5.对累加数据进行计算。

6.累减还原得到预测值。

7. 对数据进行后验差检验，得到后验差比值C 及小误差概率P 以验证建立模型是否可行。

第二部分：模型的改进1. 由于灰建模过程中的参数采用最小二乘法。

最小二乘估计是使残差平方和取得最小值时的最优解，可以保证解的无偏性，适合对数据进行一次性处理，且计算简单。

但是它求得的只是一个局部最优解，并非在任何情况下都能满足要求，最小二乘法有解的条件是B B T 矩阵非奇异（B B T 行列式数值大于零），显然B B T 是实对称阵。

在实际计算中会出现矩阵接近于奇异（行列式数值接近于零），即所谓“病态”情况。

由此导致参数估计结果不稳定，不可信，这必然导致灰预测公式的不稳定，不可信，从而使得预测结果不稳定，不可信。

实际计算中得到的灰参数为[-0.0000 52.8550 ];导致最终预测值偏大，不可采用，得到后验差比值C=0.9954，小误差概率P= 0.5028。

2. 考虑到以上情况，考虑对GM （1，1）模型进行改进。

首先对数据进行单位化，而后平滑数据，使数据之间的离散度减小。

但由于输入的数据量过大，最终得到的结果依旧不理想。

3. 再次查阅相关数据，提出新的改进方法，建立残差灰色预测模型。

将上文中得到的灰色预测值与原值的差求出，作为残差数列，对残差数列的子数列（本例中选择奇数项）重新建立GM （1，1）模型，求出残差预测数列对)1(')0(^+k e 作为)1()0(^+k x的修正模型可得)1()0(^+k x =（1-a e -）[)0(x (1)-a u ]ak e -+δ(k-i)(1-'a e -)[-)1()0(e ''a u ]''k a e - 其中δ(k-i)= i=n-n’4. 应用残差灰色预测模型后，数据的误差大为减小C= 0.5903 P= 0.7542 第三部分：模型进一步改进空间以及GM （1，1）弊端1. 残差灰色预测模型部分可加入神经网络对预测值进行修正，使得预测值更加逼近真实值2. GM （1，1）模型并不适用于大数据量的离散数据预测，在第三部分中提出的三种改进方法的作用下，才可达到勉强合格的标准。

1（k ≥i ） 0（k ＜i ）用灰色理论预测的数据所画出的负荷图(15min 一个点，共2880点)三．基于时间序列频域分析的蕴误差评价预报方法 1基于时间序列频域分析预报模型电力负荷是具有较强周期性的时间序列，因此可以对其使用时间序列频域分析方法进行分析，在指定建模时域-D 的负荷时间序列)(t P -可作如下傅里叶分解：)(t P -=)sin cos (110t w b t w a a i i i N i i ++∑-= (1) 式子中，N 为序列长度。

根据傅里叶分解的性质，分解后得到的信号是彼此正交的。

用这种方法，我们把负荷)(t P -分解成角频率为i w =i P Ni 2⨯，（i=1,2,3,…….,N-1）的分量。

通过适当的组合，并依据负荷变化周期性的特点，可将)(t P -重构如下：)()()()(0t R t W t D a t P +++=- (2)式中，)(t D 的周期为min)15(96=∆∆t t ,它是负荷中以24h 为周期变化的分量; )(0t D a +即为负荷的日周期分量;)(t W 的周期为 t ∆⨯967,是负荷的星期周期分量；)(t R 为在)(t P -中扣除)(),(,0t W t D a 之后的剩余分量，它反映了气象因素等慢变相关因素对负荷的影响以及负荷变化的随机性。

日周期分量)(0t D a +和星期周期分量)(t W 是按固定周期变化的负荷分量，因而在预报时可以直接外推。

因此，关键问题是如何对剩余分量)(t R 建立预报模型。

对剩余分量)(t R 建模应反映其主要变化规律。

综上所述可知预测便分为两个部分：①日周期分量)(0t D a +和周周期分量)(t W 的外推；②剩余分量)(t R 的预测。

2 对各负荷分量的预测2.1日周期分量)(0t D a +和周周期分量)(t W 的外推此问题本身也就转化为如何利用傅里叶分解，对(1)中的系数i a ，i b 进行求解；并根据角频率i w 的大小，按照不同的集合进行重组，依次算出)(0t D a +，)(t W 。

对此采用了频率分解算法对此问题进行处理。

2.1.1 分解结果的重构方法以电力负荷日96点采样为例：(1) )(t D 的周期为min)15(96=∆∆t t ,它是负荷中以24h 为周期变化的分量; )(0t D a +即为负荷的日周期分量。

日周期分量)(0t D a +包括的角频率的集合day Ω={}⎭⎬⎫⎩⎨⎧=⎪⎭⎫ ⎝⎛-I 0,96mod 20i i P i ωωωY 。

其中角频率0对应的是直流分量。

(2) )(t W 的周期为 t ∆⨯967,是负荷的周周期分量；包括的角频率集合为week Ω=⎭⎬⎫⎩⎨⎧≠⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-⨯I 0,96mod 0,967mod 22i i i i P P i ωωω且。

(3)扣除)(0t D a +，)(t W 之后，剩余分量为)(t R 。

2.1.2离散傅里叶变换的应用计算的目标是获得傅里叶分解后的系数i a ，i b 。

根据傅里叶分解和傅里叶变换的关系，我们可以得到傅里叶展开的系数和傅里叶变换得到的频谱间的关系。

以下是离散傅里叶变换(DFT)和离散傅里叶逆变换(IDFT)之间的变换核：nk j N n i N i p e n x X )2()()(10--=∑=ω (3)nk j N k i N ip eX N n x )2()(1)(10∑-==ω (4)根据傅里叶正交变换关系，傅里叶分解后的系数i a ，i b 和傅里叶变换后的频谱 ()i X ω之间有如下关系：()i X ω=N(i a -j i b ) (5)因此，对原有的负荷序列进行离散傅里叶变换后，可以由频谱值求得系数i a ，i b 。

求得系数后，从欧拉公式入手，利用傅里叶逆变换，求得分解后的序列)(0t D a +， )(t W 。

这里以求解日周期分量)(0t D a +为例：(1) 对原始序列)(t P -进行离散傅里叶变换(FFT)，得到()i X ω，i w =i P Ni 2⨯，（i=1,2,3,…….,N-1）。

(2) 对所有day i Ω∉ω，令()i X ω=0，得到新的频谱序列()i X ω'。

即：()i X ω'=(3) 对()i X ω'进行傅里叶逆变换后取其实部便可得)(0t D a +以上推导求解过程，同样适用于求解周周期分量)(t W2.2剩余分量)(t R 的预测事实上，)(t R 的主要变化规律是以其低频分量为代表的。

且其高频分量在实际预报中也会因多步预报的困难而难以对改善预报结果有实质性贡献。

故可通过下面滤波模型来考虑)(t R 的建模。

将)(t R 序列中每h 个点取均值。

则可进行分解。

()i X ω，day i Ω∈ω 0，其他值)()()(t H t L t R h h += （6）∑++==hk kh i h h i R t L )1(1/)()(h k t kh )1(1+≤≤+ （7）式中k h ,为整数。

)(t L h 是一阶梯状曲线，反映)(t R 的主要变化趋势，)(t H h 是分离出的高频分量，显然，h 的大小决定了)(t L h 逼近)(t R 的程度。

当h =1时有)()(t R t L h =，0)(=t H h 。

适当选取h ，可以有效的滤除)(t R 中的高频分量，并尽可能减少日负荷预报时的外推步数。

用二阶自回归模型)(t R m 表示-D 的)(48t L ：)()()(48i a i R i L i m += （8）)2()1()(21-+-=i R i R i R m m m φφ，N i 2,,4,3Λ= （9）其中i a 为误差项，)(i R m 为AR2模型，而21φφ，为模型参数。

于是式（2）可表示为：)()()()(0t R t W t D a t P m +++=-+-∈+D t t H t a i )()( 48对于式(9)中的21φφ，的求解如下：()2121111ρρρφ--=；2121221ρρρφ--= 而自相关系数()()()211∑∑=-=+∧---=N t t kN t k t t k R RRR R R ρ； 3 对预测结果的评价由所给方法得建模误差：)()()()(48t H t a t U t i I +==--ε-∈+=D t t t H I ),()(εε (10) 故有建模误差的标准差：))(()())(())((t t t t H H I I εσεεσεσ≥+=- （11）由分析可见，建模误差的大小既与)(t P -的规律性强弱有关，又与所采用的建模方法有关。

当负荷历史数据既定时，小的相对建模误差对应与好的建模方法；当建模方法既定时，小的相对建模误差对应于具有更强规律性的负荷历史数据。

具体应用时，引入预报误差方均根值的下限low γ和预报误差均方根的上限up γ两个量来评价在指定预报方法时负荷的规律性。