有理数综合测试题
七年级上册数学第一单元有理数测试题

七年级上册数学第一单元有理数测试题七年级第一单元有理数综合练一、选择题1、大于–3.5,小于2.5的整数共有()个。
A.6.B.5.C.4.D.32、如果一个数的相反数比它本身大,那么这个数为()A、正数B、负数C、整数D、不等于零的有理数3、在有理数中,绝对值等于它本身的数有()A。
1个B。
2个C。
3个D.无穷多个4、已知点A和点B在同一数轴上,点A表示数-2,又已知点B和点A相距5个单位长度,则点B表示的数是(。
)A.3.B.-7.C.3或-7.D.3或75、若两个有理数的和是正数,那么一定有结论()A。
两个加数都是正数;B。
两个加数有一个是正数;C。
一个加数正数,另一个加数为零D。
两个加数不能同为负数6、甲、乙、丙三地的海拔高度分别为20米,-15米和-10米,那么最高的地方比最低的地方高()A.10米B.15米C.35米D.5米7、对于近似数0.1830,下列说法正确的是()A.有两个有效数字,精确到千位B.有三个有效数字,精确到千分位C.有四个有效数字,精确到万分位D.有五个有效数字,精确到万分8、下列说法中正确的是()A.-a一定是负数B.a一定是负数C.-a一定不是负数D.-a2一定是负数9、每天供给地球光和热的太阳与我们的距离非常遥远,它距地球的距离约为xxxxxxxx千米,将xxxxxxxx0千米用科学记数法表示为()A.0.15×109千米B.1.5×108千米C.15×107千米D.1.5×107千米10、已知有理数x的近似值是5.4,则x的取值范围是()A。
5.35<x<5.44.B.5.35<x≤5.44.C.5.35≤x<5.45.D.5.35≤x≤5.45二、填空题1、如果数轴上的点A对应的数为-1.5,那么与A点相距3个单位长度的点所对应的有理数为-4.5.2、倒数是它本身的数是1;相反数是它本身的数是0;绝对值是它本身的数是0.3、-m+1的相反数是m-1,m+1的相反数是-(m+1)。
人教版数学七年级上册第一章有理数综合测试(含答案)

人教版数学七年级上学期 第一章有理数测试一、选择题(每小题3分,共30分)1.若a+b <0,ab <0,则( ) A. a >0,b >0 B. a <0,b <0C. a ,b 两数一正一负,且正数的绝对值大于负数的绝对值D. a ,b 两数一正一负,且负数的绝对值大于正数的绝对值 2.a,b,c 在数轴上的位置如图所示,则( )A. abc<0B. ab-ac>0C. (a-b)c>0D. (a-c)b>03.据重庆商报2016年5月23日报道,第十九届中国(重庆)国际驼子曁全球采购会(简称渝洽会)集中签约86个项目,投资总额1636亿元人民币,将数1636用科学记数法表示是( ) A. 0.1636×B. 1.636×C. 16.36×D. 163.6×104.-23+(-2×3)的结果是( ) A. 0B. -12C. -14D. -25.的相反数是( ) AB. 2C.12D. 12-6. 某地一天的最高气温是12℃,最低气温是2℃,则该地这天的温差是( ) A. ﹣10℃B. 10℃C. 14℃D. ﹣14℃7.下列说法正确的是( ) A. 零是正数不是负数 B. 零既不是正数也不是负数 C. 零既是正数也是负数D. 不是正数的数一定是负数,不是负数的数一定是正数 8.既是分数又是正数的是( ) A. 2+B. 143- C.D. 2.39.观察下图,寻找规律,在“?”处填上的数字是( ).A. 128B. 136C. 162D. 188二、填空题10. 若x=4,则|x﹣5|=_________.11.设a是最小正整数,b是最大的负整数,c是绝对值最小的有理数,则a + b + c等于____________.12.一组按规律排列数:2,0,4,0,6,0,…,其中第7个数是,第n个数是(n为正整数).13.数轴上到原点的距离等于4的数是.14.绝对值不大于2的所有整数为__________.15.-3倒数是,-3的绝对值是.三、解答题(共66分)16.用计算器计算并填空:152=________;252=________;352=________;452=________.(1)你发现了什么?(2)不用计算器你能直接算出852,952吗?17.手工拉面是我国的传统面食.制作时,拉面师傅取一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条截成了许多细细的面条,如下图所示.请问这样第几次捏合后可拉出128根面条18. 某股民在上周星期五买进某种股票1000股,每股10元,星期六,星期天股市不交易,下表是本周每日该股票的涨跌情况(单位:元)星期一二三四五(1)本周星期五收盘时,每股是多少元?(2)已知买进股票时需付买入成交额1.5%的手续费,卖出股票时需付卖出成交额1.5%的手续费和卖出成交额1%的交易费,如果在本周五收盘时将全部股票一次性地卖出,那么该股民的收益情况如何?19.阅读下列材料,解答问题.饮水问题是关系到学生身心健康的重要生活环节,东坡中学共有教学班24个,平均每班有学生50人,经估算,学生一年在校时间约为240天(除去各种节假日),春、夏、秋、冬季各60天.原来,学生饮水一般都是购纯净水(其他碳酸饮料或果汁价格更高),纯净水零售价为1.5元/瓶,每个学生春、秋、冬季平均每天买1瓶纯净水,夏季平均每天要买2瓶纯净水,学校为了减轻学生消费负担,要求每个班自行购买1台冷热饮水机,经调查,购买一台功率为500 W的冷热饮水机约为150元,纯净水每桶6元,每班春、秋两季,平均每1.5天购买4桶,夏季平均每天购买5桶,冬季平均每天购买1桶,饮水机每天开10小时,当地民用电价为0.50元/度.问题:(1)在未购买饮水机之前,全年平均每个学生要花费多少钱来购买纯净水饮用?(2)在购买饮水机解决学生饮水问题后,每班当年共要花费多少元?(3)这项便利学生的措施实施后,东坡中学当年全体学生共节约多少钱?20.在求1+2+22+23+24+25+26值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.(1)求1+3+32+33+34+35+36的值;(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.答案与解析一、选择题(每小题3分,共30分)1.若a+b<0,ab<0,则( )A a>0,b>0B. a<0,b<0C. a,b两数一正一负,且正数的绝对值大于负数的绝对值D. a,b两数一正一负,且负数的绝对值大于正数的绝对值【答案】D【解析】【详解】解:∵ab<0,∴a、b必定是异号,∵a+b<0,∴a,b两数一正一负,且负数的绝对值大于正数的绝对值.故选D.2.a,b,c在数轴上的位置如图所示,则( )A. abc<0B. ab-ac>0C. (a-b)c>0D. (a-c)b>0【答案】C【解析】【分析】由图可知a<c<0<b,据此可判断【详解】解:由图可知a<c<0<b,则abc>0,A错误;ab-ac=a(b-c)<0,B错误;(a-b)c>0,C正确;(a-c)b<0,D 错误;故选择C.【点睛】本题考查了数轴的概念,熟记数轴上右边的数大于左边的数是关键.3.据重庆商报2016年5月23日报道,第十九届中国(重庆)国际驼子曁全球采购会(简称渝洽会)集中签约86个项目,投资总额1636亿元人民币,将数1636用科学记数法表示是( )A. 0.1636×B. 1.636×C. 16.36×D. 163.6×10【答案】B【解析】试题分析:科学计数法是指a×,且,n为原数的整数位数减一.考点:科学计数法4.-23+(-2×3)的结果是( )A. 0B. -12C. -14D. -2 【答案】C【解析】【分析】按照有理数的运算法则计算即可.【详解】解:原式=-8-6=-14,故选择C.【点睛】本题考查了有理数的混合运算.5.的相反数是( )A. B. 2 C. 12D.12【答案】B【解析】【分析】根据相反数的性质可得结果.【详解】因为-2+2=0,所以﹣2相反数是2,故选B.【点睛】本题考查求相反数,熟记相反数的性质是解题的关键 .6. 某地一天的最高气温是12℃,最低气温是2℃,则该地这天的温差是( )A. ﹣10℃B. 10℃C. 14℃D. ﹣14℃【答案】B【解析】【详解】12-2=10℃.故选B.7.下列说法正确的是( )A. 零是正数不是负数B. 零既不是正数也不是负数C. 零既是正数也是负数D. 不是正数的数一定是负数,不是负数的数一定是正数【答案】B【解析】本题考查的是正、负数的意义根据正、负数的定义即可解答,零既不是正数也不是负数,故A、C错误,B正确,而不是正数的数是0和负数,不是负数的数是0和正数,故D错误,故选B.8.既是分数又是正数的是()A. 2+B.143- C. D. 2.3【答案】D【解析】本题考查的是有理数的分类大于0的数是正数.小数是分数的一种形式,所以既是分数、又是正数的数是,故选D.9.观察下图,寻找规律,在“?”处填上的数字是( ).A. 128B. 136C. 162D. 188【答案】C【解析】分析:由图中看出,从2开始,每相邻3个数的和等于第4个数,那么所求的数是26+48+88=162.详解:26+48+88=162.故选C.点睛:解决本题的关键的根据所给的数得到四个数之间的规律(从2开始,每相邻3个数的和等于第4个数).二、填空题10. 若x=4,则|x﹣5|=_________.【答案】1.【解析】试题分析:∵x=4,∴x ﹣5=﹣1<0,故|x ﹣5|=|﹣1|=1. 考点:绝对值.11.设a 是最小的正整数,b 是最大的负整数,c 是绝对值最小的有理数,则a + b + c 等于____________. 【答案】0 【解析】 【分析】根据a 是最小的正整数,b 是最大的负整数,c 是绝对值最小的有理数,得出a ,b ,c 的值,代入即可得出结论. 【详解】依题意得:a =1,b =﹣1,c =0,∴a +b +c =1+(﹣1)+0=0. 故答案为0.【点睛】本题考查了正整数、负整数的概念和绝对值的性质.熟练掌握有关概念是解答本题的关键. 12.一组按规律排列的数:2,0,4,0,6,0,…,其中第7个数是 ,第n 个数是 (n 为正整数).【答案】8,11(1)(1)2n n ++-+【解析】试题分析:观察数据可得:偶数项为0;奇数项为(n+1);故其中第7个数是(7+1)=8;第n 个数是11(1)(1)2n n ++-+. 考点:规律型:数字的变化类13.数轴上到原点的距离等于4的数是 . 【答案】±4. 【解析】试题分析:数轴上到原点的距离等于4的数有两个,是±4. 考点:1.相反数;2.绝对值.14.绝对值不大于2的所有整数为__________. 【答案】0,±1,±2 【解析】试题分析:绝对值等于2的整数是2,-2;在数轴上位于2和-2之间的整数有1,0,-1三个,它们都符合要求,所以绝对值不大于2的所有的整数是-2,-1,0,1,2. 考点:绝对值.15.-3的倒数是 ,-3的绝对值是 .【答案】-13,3.【解析】试题分析:根据乘积为1的两个数互为倒数,可得一个数的倒数;根据负数的绝对值是它的相反数,可得答案.试题解析:-3的倒数是-13,-3的绝对值是3.考点:1.倒数;2.绝对值.三、解答题(共66分)16.用计算器计算并填空:152=________;252=________;352=________;452=________.(1)你发现了什么?(2)不用计算器你能直接算出852,952吗?【答案】225 625 1 225 2 025(1)发现后两位均为25,前面的数等于原数中十位数乘比它大1的数.(2) 7 225, 9 025.【解析】试题分析:(1)通过用计算器进行计算可以发现:后两位均为25,前面的数等于原数中十位数乘比它大1的数.(2)根据(1)发现的规律可求出结果.试题解析:152=225;252=625;352=1225;452=2025(1)通过用计算器进行计算可以发现:后两位均为25,前面的数等于原数中十位数乘比它大1的数.(2)852=7225,952=9025.17.手工拉面是我国的传统面食.制作时,拉面师傅取一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条截成了许多细细的面条,如下图所示.请问这样第几次捏合后可拉出128根面条?【答案】第七次捏合后可拉出128根面条.【解析】【分析】第一次捏合后得到2根面条,第二次捏合后得到4根,第三次捏合后得到8根,据此寻找规律即可.【详解】第一次……2根面条;第二次……22根面条;第三次……23根面条;…第x次……2x根面条.于是由2x=128=27,得x=7.答:第七次捏合后可拉出128根面条.【点睛】本题考查了规律的探索.18.某股民在上周星期五买进某种股票1000股,每股10元,星期六,星期天股市不交易,下表是本周每日该股票的涨跌情况(单位:元)(1)本周星期五收盘时,每股是多少元?(2)已知买进股票时需付买入成交额1.5%的手续费,卖出股票时需付卖出成交额1.5%的手续费和卖出成交额1%的交易费,如果在本周五收盘时将全部股票一次性地卖出,那么该股民的收益情况如何?【答案】(1)9.9元;(2)亏了497.5元.【解析】试题分析:(1)用上周买入股票每股的金额加上本周股票五天的涨跌额,即可得本周星期五收盘时每股股票的金额;(2)用本周五卖出股票金额减去上周买入股票金额,减去买入成交额的手续费,减去卖出成交额的手续费,再减去卖出成交额的交易费可得收益情况.试题解析:解:(1)10+0.3+0.1﹣0.2﹣0.5+0.2=9.9(元).答:本周星期五收盘时,每股是9.9元,(2)1000×9.9﹣1000×10﹣1000×10×1.5%﹣1000×9.9×1.5%﹣1000×9.9×1%=9900﹣150﹣148.5﹣99﹣10000=﹣497.5(元).答:该股民的收益情况是亏了497.5元.考点:正负数的意义;有理数的混合运算.19.阅读下列材料,解答问题.饮水问题是关系到学生身心健康的重要生活环节,东坡中学共有教学班24个,平均每班有学生50人,经估算,学生一年在校时间约为240天(除去各种节假日),春、夏、秋、冬季各60天.原来,学生饮水一般都是购纯净水(其他碳酸饮料或果汁价格更高),纯净水零售价为1.5元/瓶,每个学生春、秋、冬季平均每天买1瓶纯净水,夏季平均每天要买2瓶纯净水,学校为了减轻学生消费负担,要求每个班自行购买1台冷热饮水机,经调查,购买一台功率为500 W的冷热饮水机约为150元,纯净水每桶6元,每班春、秋两季,平均每1.5天购买4桶,夏季平均每天购买5桶,冬季平均每天购买1桶,饮水机每天开10小时,当地民用电价为0.50元/度.问题:(1)在未购买饮水机之前,全年平均每个学生要花费多少钱来购买纯净水饮用?(2)在购买饮水机解决学生饮水问题后,每班当年共要花费多少元?(3)这项便利学生的措施实施后,东坡中学当年全体学生共节约多少钱?【答案】(1)450元;(2)4830元;(3)424080元.【解析】【分析】(1)通过每个学生每天的用水量计算出每个季节的用水量,从而计算出全年用水量;(2)购买饮水机解决学生饮水问题后,每班学生全年的花费为“水费+电费+饮水机费用”;(3)原水费-现在水费=能节约的水费.【详解】(1)因为每个学生春、秋、冬季每天购买1瓶矿泉水,夏季每天购买2瓶,所以一个学生在春、秋、冬季共要购买180瓶矿泉水,夏季要购买120瓶矿泉水,所以一年中一个学生共要购买300瓶矿泉水,所以一个学生全年共花费1.5×300=450(元).(2)购买饮水机后,一年每个班所需纯净水的桶数为:春秋两季,每1.5天4桶,则120天共要4×2 1203⎛⎫⨯⎪⎝⎭=320(桶).夏季每天5桶,共要60×5=300(桶),冬季每天1桶,共60桶,所以全年共要纯净水(320+300+60)=680(桶), 故购买矿泉水费用为680×6=4 080(元),使用电费为240×10×5001000×0.5=600(元),故每班学生全年共花费为4 080+600+150=4 830(元).(3)因为一个学生节省450-=353.4(元),所以全体学生共节省353.4×24×50=424 080(元).【点睛】本题一道实际问题,考查了通过阅读来分析题目条件,进而答题.20.在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.(1)求1+3+32+33+34+35+36的值;(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.【答案】(1)1093.5(2)2014a1 a1--【解析】【分析】(1)将1+3+32+33+34+35+36乘3,减去1+3+32+33+34+35+36,把它们的结果除以3﹣1=2即可求解;(2)将1+a+a2+a3+…+a2013乘a,减去1+a+a2+a3+…+a2013,把它们的结果除以a﹣1即可求解.【详解】解:(1)1+3+32+33+34+35+36=[(1+3+32+33+34+35+36)×3﹣(1+3+32+33+34+35+36)]÷(3﹣1)=[(3+32+33+34+35+36+37)﹣(1+3+32+33+34+35+36)]÷2=(37﹣1)÷2=2187÷2=1093.5;(2)1+a+a2+a3+…+a2013(a≠0且a≠1)═[(1+a+a2+a3+…+a2013)×a﹣(1+a+a2+a3+…+a2013)]÷(a﹣1)=[(a+a2+a3+…+a2013+a2014)﹣(1+a+a2+a3+…+a2013)]÷(a﹣1)=(a2014﹣1)÷(a﹣1)=2014a1a1--.【点睛】本题考查数字类的规律探索,有理数的混合运算,分式的运算,正确理解题意正确计算是本题的解题关键.。
“有理数”综合测试题

位 . 有
个有效 数字 . . , 小 最
6若 <4 且 为 负 整 数 . 所 有 满 足 条 件 的 的 值 是 . , 则
的 积 是 .
7 任 数 一 2, 6, 2 中 任 取 3个 相 乘 , 中 最 大 的 积 是 . 3, 0, 一 其
8察 据按 规 在 线 填 适 的 :丢弓~ … , . 数 , 律 横 上 上 当 数1 ,, 观 照 , 一 素,
1 . 能 得 f 5: 你 n小 明 所 在 位 置 卡 对 于 山 脚 的 高 度 吗 试 说 明 坪 t . 日 i t 女 子 排 球 队 共 有 1 名 队 员 , 高 分 别 为 1 3 (I. 7 1 .7 .I 0 身 7 1I 1 4(l 1 O(I. 『 7 1 f
1 6(/, 8 -1 J 5 C3, 7 m , 7 l , 7 t 1 I . 这 l 名 队 员 的 7 3 1 1 0( , 7 1 1 7c 1 9 Cl l 4 cn, 72 CI I H [ 1 l 1 O
1 . 据 测 定 , 度 每 增 加 1 m . 温 大 约 降 低 6C 小 明 在 某 座 【 上 8根 高 k 气 o. l J 发 川信 息称 他现 在 所 处位 置 的气 温 是
1. 9『 利读 下 列 材 料 . 后 解 答 问 题 . 然
一9 . 而 此 时 山 脚 下 的 气 温 为 ℃
叠
计 算 这 组 数 的 平 均 数 , ×( 2 1 5 1 5 0 2 4 _ ) 0 因 为 前 面 得 ~——+++ + + 3 = _ 每 个 数 都 减 去 了 1 5 把 这 里 的 得 数 0 再 加 上 1 5, 就 得 出 这 个 排 球 队 7 . 7
有理数单元测试题及答案

有理数单元测试题及答案一、选择题(每题2分,共10分)1. 下列哪个数是有理数?A. πB. √2C. 1/3D. 0.33333(无限循环)答案:C2. 如果a和b都是有理数,且a > b,那么下列哪个选项是正确的?A. a + b > 0B. a - b > 0C. a × b > 0D. a ÷ b > 0答案:B3. 两个负有理数相加的结果是什么?A. 正数B. 负数C. 零D. 无法确定答案:B4. 下列哪个数是无理数?A. 0.5B. √3C. 1/7D. 3.1415答案:B5. 有理数a和b的绝对值相等,且a < b,那么a和b的和是多少?A. aB. bC. 0D. -2a答案:D二、填空题(每题2分,共10分)6. 如果一个有理数的绝对值是5,那么这个数可以是______或______。
答案:5,-57. 两个有理数相除,如果商是正数,那么这两个数的符号必须______。
答案:相同8. 如果一个有理数的平方是9,那么这个数可以是______或______。
答案:3,-39. 有理数的加法运算满足交换律,即a + b = ______ + a。
答案:b10. 有理数的乘法运算满足结合律,即(a × b) × c = a ×(______ × c)。
答案:b三、计算题(每题5分,共15分)11. 计算下列表达式的值:(-3) × 2 + 4 × (-2) - 6。
答案:原式 = -6 - 8 - 6 = -2012. 计算下列表达式的值:(-4)² - 3 × 2 - 5。
答案:原式 = 16 - 6 - 5 = 513. 计算下列表达式的值:(-2)³ + 3 × (-1/3) - 1。
答案:原式 = -8 - 1 - 1 = -10四、解答题(每题10分,共20分)14. 某商店在一天内卖出了10件商品,每件商品的售价为x元,成本为y元。
《有理数》综合测试题(A)

一 . _ . . 一
4 如果 n是正 整数 , . 那么 (1 ‘ 一 ) _— — ~ .
亿 元左 右 , 将 2 0 请 8 0亿元 用科 学记 数法 表示 为
向左移 动三个 单位 长度 , 此时 A 点表 示的 数是
元.
.
5 为 了加快 3 . G网络建 设 , 电信 运营 企业 将根 据 各 自发展 规划 , 明两 年预 计 完成 3 今 G投 资 2 0 80
C A
一
A. a>b >c
C. > a> b C
l
O
1
第 2 0题 图
三 、 答题 【 计 6 解 共 O分 )
2 . 4分 ) 边 的一 段堤 岸 高 出海 平 面 l 1( 海 2米 , 附近 的一 建 筑 物高 出 海平 面 5 0米 , 里一 艘 潜水 海
艇 在 海平 面 下 3 0米 处 , 以海边 堤岸 高 度 为基 准 , 现 将其 记 为 0米 , 么 附近 建筑 物及 潜水 艇 那 的高 度各 应 如何 .
B. =0 b
C. a:0或 b:0
D. a:0和 b=0
1 。 列每 组 数 中 , 等 的是 ( 6下 相
A. 一 ) 一 一( 3 和 3 C 一( 3) l 3f . 一 和 一
) .
B. 一 +( 3)币 口一( 3) ~ D. ~ ) 一i 一( 3 和 一3{
) .
1 . 一个 数 的绝对 值 除 以这个 数 所得 的 商是 一 。 7若 1 则这 个数 一定 是 (
A 一 .l B 1或 一 . 1 C 负 数 .
D. 数 正
— — 一 —
1 . 图 , 轴 上 一 动 点 A 向 左 移 动 2个 单 位 长 度 到 达 点 , 向 右 移 8如 数 再
《有理数》考试题附答案
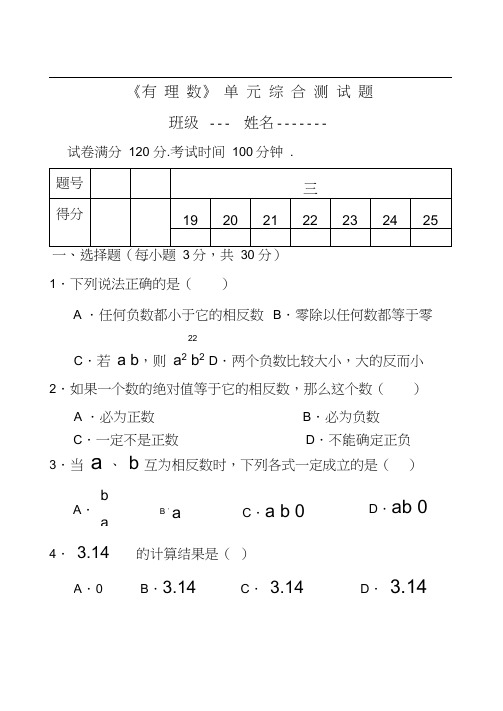
《有 理 数》 单 元 综 合 测 试 题班级 --- 姓名 -------试卷满分 120 分.考试时间 100分钟 .一、选择题(每小题 3分,共 30 分)1.下列说法正确的是()A .任何负数都小于它的相反数B .零除以任何数都等于零22C .若 a b ,则 a 2 b 2D .两个负数比较大小,大的反而小 2.如果一个数的绝对值等于它的相反数,那么这个数()A .必为正数B .必为负数 3.当a 、b 互为相反数时,下列各式一定成立的是()4. 3.14 的计算结果是( )C .一定不是正数D .不能确定正负b A .aB .aC .a b 0D .ab 0A .0B .3.14C . 3.14D . 3.145.a 为有理数,则下列各式成立的是(A.a2 0 B.1 a2 0C.( a) 0 D.a2 1 06.如果一个数的平方与这个数的绝对值相等,那么这个数是 () A.0 B.1 C.-1 D.0,1或-1 7.若 3.0860 是四舍五入得到的近似数,则下列说法中正确的是( )A.它精确到0.00001B.它精确到万分位C.它精确到0.001D.它精确到千分位8.已知a0,1 b 0,则a ,ab ,ab2按从小到大的顺序排列为( )A.a ab ab2B.ab2a ab C.a b a b2a D .a ab2ab 9. 下列各组运算中,其值最小的是( )A.( 3 2)2B.( 3) ( 2)C.( 3)2 ( 2)2D.( 3)2 ( 2)10. 几个同学在日历纵列上圈出了三个数,算出它们的和,其中错误的一个是()A .28 B.33 C.45 D.57二、填空题(每小题3分,共24 分)11.绝对值小于 5 的整数共有______________________________ 个。
12.当a b 0时,1__________ 1(填“>”“ =”或“<”)。
《有理数》综合测试题

《有理数》综合测试题
一、选择题
1、有理数“a/b”,含义是()
A、a代表数值,b代表分母
B、a代表分子,b代表数值
C、a代表分子,b代表分母
D、a代表数值,b代表分子
答案:C、a代表分子,b代表分母
2、将相似的有理数的分数表示形式进行统一叫做()
A、最小分子约分
B、同分母化
C、最大公约数化
D、最大分母约分
答案:B、同分母化
3、在实数范围内,在实数范围内,可以整除的两个有理数被称为()
A、相等有理数
B、同类有理数
C、最大公约数
D、相反有理数
答案:A、相等有理数
4、既不是正数也不是负数的是()
A、0
B、-5
C、5
D、-0
答案:A、0
5、给定min(-9/8,3/-6),则min(-9/8,3/-6)=()
A、-0.25
B、-1.25
C、-1.75
D、-2.25
答案: B、-1.25
二、填空题
1、(2/1)和____具有相同的数值。
A、(2/2)
2、有理数a/b和-a/-b是____,-a/b是____。
A、相等的;相反的
3、有理数-7/4,该数的倒数是____。
A、-4/7
4、对于两个有理数a/b、c/d,如果a/b>c/d,则a/b的数值
____c/d的数值。
A、大于
5、有理数a/b的倒数为b/a,其中a、b互质时,设有理数a/b的数值为x,则有____。
A、b/a的数值为1/x
三、计算题
1、计算(3/4)×(5/6)的值,并表示为最简分数。
答案:5/8。
人教初一数学有理数单元检测题10套

人教初一数学有理数单元检测题10套单元检测有理数单元检测001有理数及其运算(综合)(测试5)一、境空题(每空2分,共28分)1、13的倒数是____;123的相反数是____.2、比–3小9的数是____;最小的正整数是____.3、计算:3212____;95_____.4、在数轴上,点A所表示的数为2,那么到点A的距离等于3个单位长度的点所表示的数是5、两个有理数的和为5,其中一个加数是–7,那么另一个加数是____.6、某旅游景点11月5日的最低气温为2,最高气温为8℃,那么该景点这天的温差是____.C7、计算:(1)100(1)101______.8、平方得214的数是____;立方得–64的数是____.9、用计算器计算:95_________.10、观察下面一列数的规律并填空:0,3,8,15,24,_______.二、选择题(每小题3分,共24分)11、–5的绝对值是()A、5B、–5C、15D、1512、在–2,+3.5,0,23,–0.7,11中.负分数有()A、l个B、2个C、3个D、4个13、下列算式中,积为负数的是()A、0(5)B、4(0.5)(10)C、(1.5)(2)D、(2)(1)(253)14、下列各组数中,相等的是()A、–1与(–4)+(–3)B、3与–(–3)C、324与916D、(4)2与–1615、小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是()A、90分B、75分C、91分D、81分16、l米长的小棒,第1次截止一半,第2次截去剩下的一半,如此下去,第6次后剩下的小棒长为()A、112B、132C、1164D、12817、不超过(32)3的最大整数是()A、–4B–3C、3D、418、一家商店一月份把某种商品按进货价提高60%出售,到三月份再声称以8折(80%)大拍卖,那么该商品三月份的价格比进货价()A、高12.8%B、低12.8%C、高40%D、高28%单元检测三、解答题(共48分)19、(4分)把下面的直线补充成一条数轴,然后在数轴上标出下列各数:–3,+l,21,-l.5,6.2要使这杯酒精冻结,需要几分钟?(精确到0.1分钟)25、(4分)某商店营业员每月的基本工资为300元,奖金制度是:每月完成规定指标10000元营业额的,发奖金300元;若营业额超过规定指标,另奖超额部分营业额的5%,该商店的一名营业员九月份完成营业额13200元,20、(4分)七年级一班某次数学测验的平均成绩为80分,数学老师以平均成绩为基准,记作0,把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10,–15,0,+20,–2.问这五位同学的实际成绩分别是多少分?21、(8分)比较下列各对数的大小.(1)43525与4(2)45与45(3)52与2(4)23与(23)222、(8分)计算.(1)38715(2)12(1146)(3)236(3)2(4)(4)1(11163)623、(12分)计算.(l)43(2)215(2)1.530.750.53343.40.75(3)(10.5)132(4)2(4)(5)3(35)32(22)(114)24、(4分)已知水结成冰的温度是0C,酒精冻结的温度是–117℃。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有理数综合测试题Revised on November 25, 2020
有理数综合测试题姓名
一、选择题(本题共有10个小题,每小题都有A、B、C、D四个选项,请你把你认为适当的选项前的代号填入题后的括号中,每题3分,共30分)
1、下列说法正确的是()
A 整数就是正整数和负整数
B 负整数的相反数就是非负整数
C 有理数中不是负数就是正数
D 零是自然数,但不是正整数
2、下列各对数中,数值相等的是()
A -27与(-2)7
B -32与(-3)2
C -3×23与-32×2
D ―(―3)2与―(―2)3
1,-,-,-2,-212各数中,最大的数是()
3、在-5,-
10
1 C - D -5
A -12
B -
10
4、若其中至少有一个正数的5个有理数的积是负数,那么这五个因数中,正数的个数是()
A 1
B 2或4
C 5
D 1和3
5、绝对值大于或等于1,而小于4的所有的正整数的和是()
A 8
B 7
C 6
D 5
6、计算:(-2)100+(-2)101的是()
A 2100
B -1
C -2
D -2100
7、比-大,而比1小的整数的个数是()
A 6
B 7
C 8
D 9
8、如果一个数的平方与这个数的差等于0,那么这个数只能是()
A 0
B -1
C 1
D 0或1
9、我国最长的河流长江全长约为6300千米,用科学记数法表示为()
A 63×102千米
B ×102千米
C ×104千米
D ×103千米
10、已知=,若x2=,则x的值等于()
A B ± C ± D ±86
二、填空题(本题共有8个小题,每小题3分,共27分)
11、一幢大楼地面上有12层,还有地下室2层,如果把地面上的第一层作为
基准,记为0,规定向上为正,那么习惯上将2楼记为;地下第一层记作;数-2的实际意义为,数+9的实际意义为。
12、互为相反数的两数(非零)的和是,商是;互为倒数的两数的
积是。
13、某数的绝对值是5,那么这个数是。
134756≈(保留四个有效数字)
2)3=。
14、( )2=16,(-
3
1的点表示的有理数是。
15、数轴上和原点的距离等于3
2
16、计算:-×178
+14×72-(14×73-179×= 。
17、使用计算器进行计算时,按键程序为
,则结果为 。
18、+的相反数与-的绝对值的和是 。
19、已知每辆汽车要装4个轮胎,则51只轮胎至多能装配 辆汽车。
三、解答题(本题共有7个小题,满分63分)
20、计算:(本题共有7个小题,每小题4分,共28分)
(1)8+(―4
1)―5―(― (2)―82+72÷36 (3)721×143÷(-9+19) (4)25×43―(―25)×21+25×(-4
1) (5)(-81)÷241+9
4÷(-16) (6)(-1)3-(1-21)÷3×[2―(―3)2] (7)3232)2(361)3()2(---⨯
---
21、一天小明和冬冬利用温差来测量山峰的高度。
冬冬在山脚测得的温度是4℃,小明此时在山顶测得的温度是2℃,已知该地区高度每升高100米,气温下降℃,问这个山峰有多高(5%)
22、有一种“二十四点”的游戏,其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24。
例如对1,2,3,4,可作如下运算:(1+2+3)×4=24(上述运算与4×(1+2+3)视为相同方法的运算)
现有四个有理数3,4,-6,10,运用上述规则写出三种不同方法的运算式,可以使用括号,使其结果等于24。
运算式如下:(1) ,
(2) ,(3) 。
另有四个有理数3,-5,7,-13,可通过运算式(4) 使其结果等于24。
(8%)
23、下表列出了国外几个城市与北京的时差(带正号的数表示同一时刻比北京的时间早的时数)。
现在的北京时间是上午8∶00 (1)求现在纽约时间是多少 (2)斌斌现在想给远在巴黎的姑妈打电话,你认为合适吗5%
24、画一条数轴,并在数轴上表示:和它的相反数,-2
1和它的倒数,绝对值等于3的数,最大的负整数和它的平方,并把这些数由小到大用“<”号连接起来。
(6%)
25、甲、乙、丙三位同学合乘一辆出租车同往一个方向,事先约定三人分摊车
资。
甲在全程的31处下车,乙在全程的3
2处下车,丙坐完全程下车,车费共54
元。
问甲、乙、丙三位同学各付多少车费比较合理请你设计一个方案。
(6%)
26、某数学俱乐部有一种“秘密”的记帐方式。
当他们收入300元时,记为-240;当他们用去300元时,记为+360。
猜一猜,当他们用去100元时,可能记为多少当他们收入100元时,可能记为多少说说你的理由。
(5%)
四、提高题(本题有2个小题,每小题10分,共20分)
1、右面是一个正方体纸盒的展开图,请把-10,7,10,-2,-7,2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两数互为相反数。
2、若a、b、c均为整数,且∣a-b∣3+∣c-a∣2=1,求∣a-c∣+∣c-b ∣+∣b-a∣的值。
