大连理工大学数字电路与系统第2章 逻辑代数答案(部分)
大工《数字电路与系统》课程考试模拟试卷A答案

机密★启用前大连理工大学网络教育学院2014年8月份《数字电路与系统》课程考试模拟试卷答案考试形式:闭卷试卷类型:A一、单项选择题(本大题共6小题,每小题3分,共18分)1.B 2.C 3.C 4.B 5.A 6.C二、填空题(本大题共10空,每空2分,共20分)1.(1) 213(2) 12.04(3) 40D(4) 10101001.11002.题号原码反码补码十进制数(1) 10111 01000(2) 1,011100 1,011101(3) 0,10101.01 +21.25三、化简题(本大题共3小题,每小题6分,共18分)=++1.答:F XYZ XY XY ZXY XY=+(3分)=(3分)Y2.答:填卡诺图,圈1,得到最简与或表达式。
CD AB00101101101111001110011100011110(3分)Y B AD A CD ∴=++ (3分)3.证明:0A ⊕00A A =+ (3分) A = (3分)四、简答题(本大题共3小题,第1、2小题各7分,第3小题10分,共24分)1.答:QQ OO ttSR O Ott(错1处扣1分,图都正确7分满分)2.答: ln()DD T T DD T T V V V T RC V V V -++--=- (3分)3812 2.7 6.3201010ln()s 12 6.3 2.7--=⨯⨯⨯⨯- (2分)0.267ms 267μs == (2分)3.答:(1)3ref f 322821016V 210V FSR R R ⨯⨯⨯===⨯ (2分) (2)当123011X X X =时,333166V 28o V FSR=-=-⨯=- (2分) 当123110X X X =时,3661612V 28o V FSR =-=-⨯=- (2分)(3),min 311162V 28o V FSR=-=-⨯= (2分)(4)3,max 32171614V 28o V FSR -=-=-⨯=- (2分)五、计算题(本大题1小题,共20分)1.答:(1)分析。
大连理工大学线性代数第二章书后习题答案2

习题2-11. 32A =6.2. 用行列式的定义计算下面的行列式.(1)35;(2)256;(3)8;(4)29.--思考题 2-21.若对方阵A 进行一次对调变换得到B ,则=-A B ;若对方阵A 进行一次倍乘变换(假设第i 行或第i 列乘以数k )得到B ,则k =B A ;若对方阵A 进行一次倍加变换得到B ,则.=A B2.0.=A3.(1)不正确。
例如,设1112111221222122,,a a b b a a b b ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦A B 则 1111121211121211121221212222212222212222a b a b a a b b a b a b a b a a b b a b +++++==+++++A B 111211121112111211121112212221222122212221222122a a ab b a b b a b b a a a a b b a b b a b b a =+++=+++A B(2)不正确。
设A 的阶数为n ,则(1)n-=-A A(3)不正确。
例如,设1200⎡⎤=⎢⎥⎣⎦A ,则0,=A 但.≠A O 4. ,,1,(),()1i j i i j k k k =-==E E E5. 性质2-2讲的是方阵A 的第i 行(列)的数与第i 行(列)对应的代数余子式的乘积之和等于A 的行列式;性质2-7讲的是方阵A 的第i 行(列)的数与另一行(列)对应的代数余子式的乘积之和等于0.习题2-21. 2111231123123det()3,,39,,9,,18.c c a a a a a a a a a a a -=+-=-+=-=-A2. 131223123233122312312323,2,3,,3,,3,,6c c c c c c -+--++=-===a a a a a a a a a a a a a a a a3.321123211321212311223,,,,,,,,,,,,,,,n m +=+=-+=-a a a b b a a a b a a a b a a a b a a b a4.证:(1)将第2列和第3列都加到第1列,得00.0a b b c c ab c c a b c c a a b c a a b c aa bb ca b b c --------=--=----- (2)111111111111111122222222222222223333333333333333a b b c c a a b c c a b b c c a a b b c c a a b c c a b b c c a a b b c c a a b c c a b b c c a ++++++++++=++++++++++++1111111111111111122222222222222222333333333333333332a b c c b c c a a b c b c a a b c a b c c b c c a a b c b c a a b c a b c c b c c a a b c b c a a b c ++=+++=+=++ (3)设A 的阶数为n ,则n 为奇数.由A 是反称矩阵,得T =-A A .两边取行列式,得 ,(1),,T n =-=-=-A A A A A A 故0.=A5. 先按行提公因式,在按列提公因式,得2111121211221212222221122n n n nn n n n nn n a b a b b a b b a b b a b a b b a b b a b b a b11112212112222121122n n n nnn n nn na b a b a b a b a b a b b b b a b a b a b =1112121222222222121212n n nn n n nna a a a a ab b bb b bc a a a ==6.(1)解:先按行提公因式,在按列提公因式,得1111114111ab ac aebd cd de abcdef abcdef bfcfef---=-=--(2)103100204310043141992003951200510012520301300600130013=--=--=提高题2-21.,,,,,,+=++++=+-++A B ξηαββγαγξηαγβγαγ ,,,,,,22,,,=+-++=+-+=+ξηαγβγαγξηαγβγγξηαβγ 2(,,,,,,)2()6=+=+=ξαβγηαβγA B2.1231231231232323,24,36,3,25=++++++=++++B a a a a a a a a a a a a a a a a 1232331223123,3,,,,,2=+++-=-+=-=-a a a a a a a a a a a a a 3.根据性质2-7,得 414243444142434411110A A A A A A A A +++=⋅+⋅+⋅+⋅=4.(1)132343(1)(1)52(1)301(1)415D +++=-⋅-+⋅-++⋅-=-. (2) 1424449(1)(1)52(1)01(1)40,2a a +++-⋅-+⋅-++⋅-==-.5.(1)对第2行和第4行分别应用性质2-2和性质2-7,得212223242521222324254()3()4,2()()0A A A A A A A A A A ++++=⎧⎨++++=⎩ 解得2122232A A A ++=-.(2)对第2行和第4行分别应用性质2-7,得 313233343531323334354()3()0,2()()0A A A A A A A A A A ++++=⎧⎨++++=⎩ 解得313233A A A ++=0.思考题 2-31.212r r -表示第二行先乘以2,再用第二行减去第一行,212232311212r r -=.2.对行列式进行对调变换和倍乘变换时,需要在得出的行列式的前面添加负号和系数,对行列式进行初等变换时,关心的是最后的数值;对矩阵进行初等变换时不需要添加负号和系数,对矩阵进行初等变换时,关心的是用何种变换进行化简,最后化成何种形式。
电路与电子技术基础第2章习题参考答案
100k I 100k 500/101k + 16Ω U (c)
500 0.98 × 103 I e 101
I
10600/101k
-
+
Ie
+
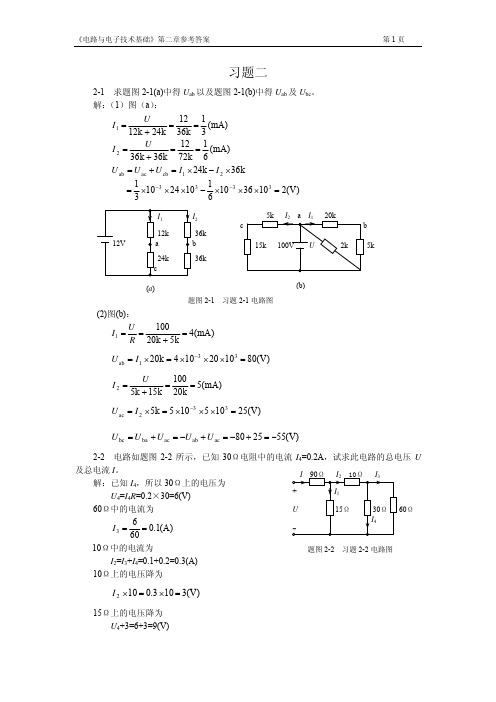
(1)求 Ri,即求 U 和 I 的关系,运用电源等效互换逐步化简(a)。 500k 电阻与 5k 电阻并联
500 × 5 500 = k 500 + 5 101 把 0.98Ie 受控电流源化为受控电压源 500 500 U s = 0.98 I e × × 10 3 Rs = × 10 3 Ω 101 101 500 合并 100k 与 k 串联电阻得 101 500 10600 得图(c) 100 + = × 10 3 101 101 16Ω上的压降为 U Ie = − U = − I e × 16 16 两支路并联,另一支路上的压降为 500 // 5 =
(f)
解:运用等效电阻的概念,电路逐步化简为图(f)单一回路。 图(f)中:
1 Ua = U 2 1 1 图(e)中: Ub = Ua = U 2 4 1 1 图(c)中: Uc = Ub = U 2 8 1 1 图(a)中: Ud = Uc = U 2 16 2-8 求题图 2-8 电路中的 U。
《电路与电子技术基础》第二章参考答案
第5页
U s1 = 50 × 6 = 300(V) U s 2 = 25 × 6 = 150(V) U s 2 = 25 × 6 = 150(V)
电路的总电流
Rs1 = 6(Ω) Rs1 = 6(Ω) Rs2 = 6(Ω)
I=
则
150 + 150 75 = (A) 12 + 24 9
数字电路课后习题答案第二章

2.8
(a)
(b)
2.9
(a)
(b)
2.10 (a)
(b)
(c)
2.11 decimal signed-magnitude two’s-magnitude one’s-complement 2.12 (a)
11010100 (b) 101110011 (c) 01011101 (d) 00100110 + 10101011 + 11010110 + 00100001 + 01011010 ------------------------------------------------------------------------------------------------------------------------01111111 10001111 01111101 10000000 yes no no yes
2.6
(a) (c) (e) (g) (i)
125 10 = 1111101 2 209 10 = 11010001 2 132 10 = 1000100 2 727 10 = 10402 5 1435 10 = 2633 8 1100010 110101 + 11001 ------------------------1001110 110000 110101 - 11001 -----------------------011100 1372 + 4631 ------------------6223 1372 + 4631 ------------------59A3 (b)
2.7
(a)
111111110 (d) 11000000 1011000 (c) 11011101 101110 1110010 + 1100011 + 100101 + 1101101 ------------------------------------------------------------------------------------101000000 1010011 11011111 0011010 000010 (c) 11000100 (d) 1110010 11011101 101110 - 1101101 - 1100011 - 100101 ------------------------------------------------------------------------------------0000101 01111010 001001 47135 + 5125 ------------------54262 4F1A5 + B8D5 ---------------------5AA7A + 18 00010010 00010010 00010010 (c) 175214 (d) 110321 + 152405 + 56573 ---------------------------------------------347621 167114 F35B + 27E6 -------------------11B41 + 115 01110011 01110011 01110011 (d) 1B90F + C44E --------------------27D5D +79 01001111 01001111 01001111 –49 10110001 11001111 11001110 –3 10000011 11111101 11111100 –100 11100100 10011100 10011011
数字电路与数字电子技术 课后答案第二章

1.有一分立元件门电路如图P2.1 ( a )所示,歌输入端控制信号如图p2.1 ( b )所示.。请对应图( b )画出输出电压 的波形。
( a )
图P2.1
解:
2.对应图P2.2所示的电路及输入信号波形画出 、 、 、 的波形。
图P2.2 ( a )
解:
F1, F2, F3, F4为图P2.2A
(b) TTL非门的输出端不能并联,应换为集电极开路门。
(c)输入端所接电阻 ,相当于”0”,使 =1,必须使 ,如取
(d)输入端所接电阻 相当于”1”,使 ,必须使 ,如取 ,相当于”0”,这时
7.电路如图P2.7 ( a ) ~ ( f )所示,已知输入信号A,B波形如图P2.7 ( g )所示,试画出各个电路输入电压波形。
(b)
可用于TTL门电路,原因同上.
13.试说明下列各种门电路中有哪些输出端可以并联使用:
(1)具有推拉式输出端的TTL门电路;
(2) TTL电路的OC门;
(3) TTL电路的三态门;
(4)普通的CMOS门;
(5)漏极开路的CMOS门;
(6) CMOS电路的三态门.
解:
(1)具有推拉式输出端的TTL门电路输出端不能并联,否则在一个门截止,一个门导通的情况下会形成低阻通路,损坏器件。
(b)
这种扩展输入端的方法不适用于TTL电路因为当扩展端C、D、E均为低电平时,三个二极管均截止,或非门的一个对应输入端通过100K 电阻接地,此时 ,将输入信号A,B封锁,电路工作不正常。
12.试分析图P2.12(a),(b)电路的逻辑功能,写出y的逻辑表达式,图中门电路均为CMOS门电路,本电路能否用于TTL门电路,并说明原因。
大连理工大学22春“电力系统自动化技术”《数字电路与系统》期末考试高频考点版(带答案)试卷号1

大连理工大学22春“电力系统自动化技术”《数字电路与系统》期末考试高频考点版(带答案)一.综合考核(共50题)1.时序图不可以用来描述时序逻辑电路。
()A.错误B.正确参考答案:A2.D/A转换后的模拟输出电压一定是原码的数值部分转换得到的。
()A.错误B.正确参考答案:B3.存储器的主要技术指标有()。
A.字长B.CPUC.存取容量D.存取周期参考答案:CD4.组合逻辑电路的构成具有哪些特点?()A.电路的输出与输入之间不存在反馈电路B.电路中不含记忆单元C.电路中不含延迟单元D.电路中的信号是单向传输的参考答案:ABCD下列哪个不是计数器的功能?()A.计数B.分频C.存储D.顺序控制参考答案:C6.时序逻辑电路要想完全描述功能,必须要有下列哪些方程?()A.特性方程B.激励方程C.状态方程D.输出方程参考答案:BCD7.TTL与非门和TTL非门相比较,下列说法正确的是()。
A.结构不同B.结构相同C.输入端个数不同D.输入端个数相同参考答案:BC8.组合逻辑电路设计是组合逻辑电路分析的逆过程。
()A.正确B.错误参考答案:A9.R-2R倒梯形电阻网络DAC电路的模拟电压输出与R-2R梯形电阻网络DAC电路的模拟电压输出相比,()。
A.前者大B.二者相同D.二者大小不定参考答案:B10.下列哪些可以用来构成多谐振荡器?()A.555定时器B.TTL与非门C.石英晶体D.施密特触发器参考答案:ABCD11.电脉冲是指一定时间内出现的电压或电流的变化。
()A.错误B.正确参考答案:A12.寄存器74194不可用于计数器。
()A.正确B.错误参考答案:B13.PAL是采用双极型工艺制作,熔丝编程方式的可编程逻辑器件。
()A.正确B.错误参考答案:A14.TTL与非门构成的多谐振荡器和对称式多谐振荡器不是同一种振荡器。
()B.错误参考答案:B15.同步计数器有外部输入变量。
()A.正确B.错误参考答案:B16.下列关于多变量异或运算说法中,正确的是()。
数字电路与系统_大连理工大学中国大学mooc课后章节答案期末考试题库2023年

数字电路与系统_大连理工大学中国大学mooc课后章节答案期末考试题库2023年1.ASM图是数字系统控制过程的算法流程图,表示了所有操作的准确时间序列,精确到一个时钟周期。
参考答案:正确2.把256×2的RAM,扩展成256×4的RAM,需要2片256×2的RAM。
参考答案:正确3.设计三种图案彩灯控制系统的控制器。
三种图案彩灯依次循环亮,其中苹果形图案灯亮16 s,香蕉形图案灯亮12 s,葡萄形图案灯亮9 s。
用逻辑变量A、B、G分别表示苹果灯、香蕉灯、葡萄灯。
用逻辑变量X、Y、Z分别表示计时信号16s、12s、9s。
下列ASM图正确表示了该灯光控制系统。
【图片】参考答案:错误4.计数器不是时序逻辑电路。
参考答案:错误5.已知有DAC电路,如下图所示。
其中【图片】,【图片】=5伏,当输入二进制数为110时,输出电压是多少?【图片】参考答案:-3.75 伏6.观察下列电路,Vref=10伏,如果输入二进制数为1000000000时,输出电压多少?【图片】参考答案:0 伏7.一般来说,时序逻辑电路由组合电路和触发器两部分组成。
参考答案:正确8.74161是一款模15的计数器。
参考答案:错误9.74163是异步清零、同步置数的计数器。
参考答案:错误10.如果用卡诺图化简逻辑函数,拟得到最简或与式,应该在卡诺图上圈0。
参考答案:正确11.具有直接输入端的触发器,其直接输入端有最高优先权,可以直接决定触发器的状态。
参考答案:正确12.在用卡诺图求逻辑函数的最简与或式的时候,如果有一个圈中的1都被别的圈包含了,那么可以断定:这个圈是多余的。
参考答案:正确13.用74290实现模40的计数器,至少需要2片74290。
参考答案:正确14.把石英晶体加入多谐振荡器电路中,其目的是让频率更稳定。
参考答案:正确15.观察下图,该多路数据选择器完成的逻辑函数是【图片】【图片】参考答案:正确16.已知一个数字系统,有5个独立状态。
数字电子技术基础课后习题答案第2章习题答案

思考题:题2.1.1 答:肖特基二极管(SBD)、分流。
题2.1.2 答:基区、滞后。
题2.1.3 答:(A)、(B) 。
题2.1.4 答:对。
题2.2.1 答:A、B。
题2.2.2 答:C、D。
题2.2.3 答:4ns。
题2.2.4 答:(A)、(C)、。
题2.2.5 答:降低、降低。
题2.2.6 答:0、1和三态题2.2.7 答:若一个输出高电平,另一个输出低电平时,会在T4和T5间产生一个大电流,烧毁管子。
OC门“线与”在输出接一电阻和一5-30V电源电压。
题2.2.8 答:能、分时。
题2.2.9 答:1. 为了缩短传输延迟时间,电路中使用肖特基管和有源泄放电路,另外,还将输入级的多发射极管改用SBD代替,由于SBD没有电荷存储效应,因此有利于提高电路的工作速度。
电路中还接入了D3和D4两个SBD,当电路的输出端由高电平变为低电平时,D4经T2的集电极和T5的基极提供了一条通路,一是为了加快负载电容的放电速度,二是为了加速T5的导通过程。
另外,D3经T2的集电极为T4的基极提供了一条放电通路,加快了T4的截止过程。
2. 为降低功耗,提高了电路中各电阻的阻值,将电阻R5原来接地的一端改接到输出端,以减小T3导通时电阻R5上的功耗。
题2.3.1 答:A。
题2.3.2 答:A。
题2.3.3 答:A。
题2.3.4 答:导通。
题2.3.5 答:B、C。
思考题:题2.4.1 答:(A)分流。
题2.4.2 答:(B) 内部电阻和容性负载。
题2.4.3 答:(B) 3.3V;(C)5V;(D) 30V。
题2.4.4 答:CMOS反相器和CMOS传输门。
题2.4.5 答:加入缓冲器保证输出电压不抬高或者降低,正逻辑变负逻辑或者相反,与非变成或非,或者或非变为与非。
题2.4.6 答:(C)低、高。
题2.4.7答:(A) OD门;(B) OC门;(C)三态门。
16题2.4.8 答:(A)驱动大负载;(B)电平移位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
再对偶 F9 =( A + C)( A + D)( A + B) =A + BCD
(10) ABC + A C(B + D)CD 解: F10 = ABC + A + C + BD + C + D = A + B + C + D
X= ABD + ABCD + BCD + ( A + B)C ( B + D)
解: = ABD + ABCD + BCD + BC + ACD
= ( B + D)(B+C )
3.12 化简下列各式成最简与或式。
(1) G = AB + BC + AC 解: G =AB + BC =( A + B)(B + C)= AB+BC
解:(a) Y = AB ⋅ BC ⋅C = AB + BC + C = AB + C
(b) F1= AB + A ⊕ B ⋅C= AB + ( AB + AB)C= AB + ABC + ABC= AB + AC + BC
F2 = A ⊕ B ⊕ C
3.21 利用函数的随意状态化简函数,并求出最简与或式。 (1) G = Y + X Z, d = YZ + XY
解: F3 (A, B,C, D) = BD + BD + BC 或 F3 (A, B,C, D) = BD + BD + CD
或
(6) F6 (A, B,C, D) = m∑ (0,1, 4,6,8,9,10,12,13,14,15)
解: F6 (A, B,C, D) = AB + BC + BD + AD
3.19 试用最少与非门实现下列逻辑函数。 (1) Y = A C + AB C + ABC
解: Y1 = AC + ABC + ABC = AC + BC = AC ⋅ BC
或 Y1 =( A + AB + AB)C =( A + B)C =AB ⋅ C (3) Y = AB + AC + ABC
解: Z=3 A C D + BD + CD
(5) Z5 = Σm (0,2,7,8,13,15) +Σd (1,5,6,9,10,11,12)
解: Z5 = BD + BD = B D
3.23 用 VEM 化简逻辑函数。 (2) X = A B C D + A BC D + AB CD + AB C D + ABC D + ABCD ,将变量 D 作为
(3) X = (B + C + D)(A + C + D)(A + C + D)(A + B + D) 解: X ' = BCD + AC D + AC D + ABD = BCD + C D + ABD
X = (B + C + D)(C + D)( A + B + D)
( ) (7) X = ABD + ABCD + BCD + AB + C ( B + D)
6
解: G1 = 1
= (3) G( A, B,C, D) ∑ m(0, 1, 5, 7, 8, 11, 14) + ∑ d (3, 9, 15)
解: G3 = B C + AD + ABC + CD 或 G3 = B C+AD+ABC+BD
(5) G( A, B,C, D) = A + C + D + ABCD + ABCD ,=d AB + AC 解: G5 =AD + ACD + ABD
(3) ( A + B)( B + D)(C + D)( A + C + D)( B + C + D)
解:取对偶式
F
' 3
=
AB
+
BD
+
CD
+ABiblioteka D+BCD
= AB + BD + CD + AD + BCD
= AB + BD + CD + AD + BC
F 3 = ( B + D)( A + D)C 再对偶 = ( AD + BD)C
或 G5 =AD + ACD + BCD
5
3.22 化简下列具有约束条件为 d =AB + AC 的逻辑函数。 (1) Z1 = A C + AB , d =AB + AC
解:= Z1 A C + B (3) Z 3 = A C D + ABCD + A BD + AB CD , d =AB + AC
( ) (20) AC (CD + AB) + BC B + AD + CE
解: F=20 BC ( B + AD)(C + E=) ABCDE
3.11 化简下列各式为最简或与式。 (1) X = (A + B)(B + C)(A + C)(A + C)(B + C)
解: X ′ = AB + BC + AC + AC + BC = AB + AC + BC X =( A + B)( A + C)(B + C)
3
解: F3 = BD + AD + A B D + ABC 或 = BD + AD + A B D + AC D =( A + B + D)(B + C + D)( A + D)
(7) F7 = ABC + AB + AB + BC + AD
( ) 解: F7 = AB + AC + AD =A B+C+D
(3) G = ( A ⊕ B)C + (B ⊕ C)D
2
G = ( A B + C )( B C + D)
= ( AB + AB + C)(BC + BC + D) 解: = ABC + ABD + ABC + ABD + BC + C D
= ABC + ABD + ABD + BC + C D = ABC + ABD + BC + C D
解:Y3 = AB + (A + B)C = (A + B)(A⋅ B + C) = A B + A C + B C = A B ⋅ A C ⋅ B C
3.20 写出题图 3.20 中各逻辑图的逻辑函数式,并化简为最简与或式。
4
A
B
1
&
A B
& ≥1 1
F1
C
&
Y
=1
C
1
&
=1
F2
(a)
(b)
题图 3.20
( ) ( ) (5) G =BC + ABCE + B AD + AD + B AD + AD
解: G = BC + AD + AD
3.15 用卡诺图化简下列函数,并求出最简与或表达式。
(1) F1(A, B,C) = m∑ (2, 3, 6, 7)
解: F1( A, B,C) = B
(3) F3 (A, B,C, D) = m∑ (1, 3, 4, 6, 7, 9, 11, 12, 14, 15)
引入卡诺图的变量。 解:= X 2 B D + AB
3.24 用 VEM 化简下列逻辑函数,将变量 C、D 作为引入卡诺图的变量。 (2)Y = ABCD + ABCD + ABC D + ABC D + ABCD + ABC D + A B CD + ABCD
解:= Y2 A B CD + AC + BCD + AB
(11) X + Y ⋅ X + Y 解: F11 = X Y ⋅ XY = 0
1
(18) ( A + BC )( A + DE)
解: F18 = ABC + ADE = AB + AC + AD + AE
(19) ABCD + ABD + ACD 解: F19 = ABD + ACD + ACD = AD
第二章 逻辑代数 作业答案
3.8 用公式法化简下列逻辑函数。
(1) AB + BC + BC + AB
解:
方法一: F1 = AB + BC + BC + AB + AC = BC + AB + AC
