(完整版)八年级数学几何经典题【含答案】
初二几何考试题及答案

初二几何考试题及答案一、选择题(每题3分,共15分)1. 在一个直角三角形中,一个锐角是30°,另一个锐角的度数是多少?A. 60°B. 45°C. 30°D. 90°答案:A2. 一个等腰三角形的底边长为6厘米,腰长为8厘米,那么这个三角形的周长是多少?A. 22厘米B. 26厘米C. 30厘米D. 34厘米答案:B3. 下列哪个图形是轴对称图形?A. 平行四边形B. 等腰梯形C. 任意三角形D. 不规则五边形答案:B4. 一个圆的半径为5厘米,那么这个圆的面积是多少?A. 78.5平方厘米B. 25π平方厘米C. 50π平方厘米D. 100π平方厘米答案:C5. 一个等边三角形的边长为10厘米,那么这个三角形的高是多少?A. 5厘米B. 10厘米C. 15厘米D. 20厘米答案:C二、填空题(每题3分,共15分)6. 一个等腰三角形的两个底角相等,如果一个底角为40°,那么顶角的度数是________。
答案:100°7. 一个圆的周长为31.4厘米,那么这个圆的半径是________厘米。
答案:58. 在一个平行四边形中,如果一组对边的长度分别为8厘米和6厘米,那么这个平行四边形的周长是________厘米。
答案:289. 一个直角三角形的两条直角边长分别为3厘米和4厘米,那么这个三角形的斜边长是________厘米。
答案:510. 一个扇形的圆心角为60°,半径为4厘米,那么这个扇形的面积是________平方厘米。
答案:6.28三、解答题(每题10分,共20分)11. 已知一个等腰三角形的底边长为10厘米,腰长为12厘米,求这个三角形的面积。
解答:首先,我们需要找到等腰三角形的高。
由于等腰三角形的两个底角相等,我们可以将底边平分,得到两个直角三角形。
每个直角三角形的底边为5厘米(10厘米的一半),斜边为12厘米。
初中数学几何证明经典试题(含答案)【范本模板】
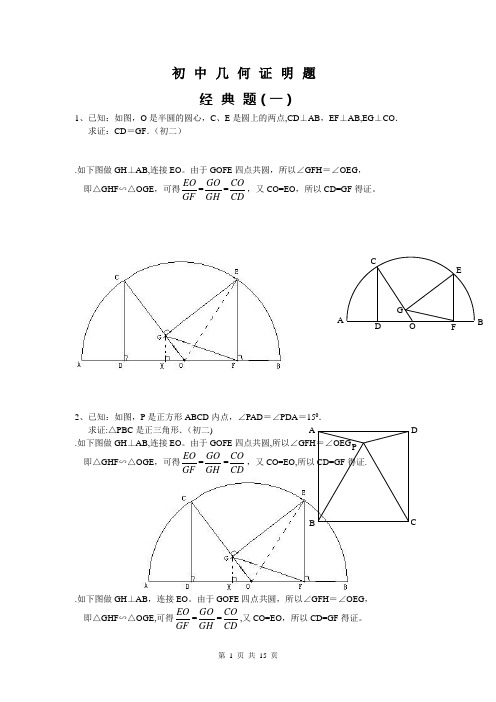
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证..如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典 1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
完整版)八年级数学上册几何经典

完整版)八年级数学上册几何经典1.在△ABC中,AB=AC,∠A=40°,BP=CE,BD=CP,则∠DPF=()。
改写:已知△ABC中,AB=AC,∠A=40°,BP=CE,BD=CP,求∠DPF的度数。
2.如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为()。
改写:如图所示,正五边形ABCDE中,直线l∥BE过顶点A,求∠1的度数。
3.如图,在3×3的正方形网格中,∠1+∠2+∠3+∠4+∠5=()。
改写:如图所示,3×3的正方形网格中,求∠1+∠2+∠3+∠4+∠5的度数和。
4.在一个n边形中,除了一个内角外,其余(n-1)个内角的和为2750°,则这个内角的度数为()。
改写:在一个n边形中,除了一个内角外,其余(n-1)个内角的和为2750°,求这个内角的度数。
5.如图,在△ABC中,AB=AC,D点在AB上,DE⊥___于E,EF⊥BC于F。
若∠BDE=140°,则∠DEF等于()。
改写:如图所示,在△ABC中,AB=AC,D点在AB上,DE⊥___于E,EF⊥BC于F。
已知∠BDE=140°,求∠DEF的度数。
6.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为()。
改写:如图所示,AD是△ABC的角平分线,DF⊥AB,垂足为F,___ADG和△AED的面积分别为50和39,求△EDF的面积。
7.如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是()。
改写:如图所示,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1.将___沿直线AD翻折,使点C落在AB边上的点E处。
初二数学几何题50道,要带答案带过程

初二数学几何题50道,要带答案带过程选择题:1. 若两角互为补角,则它们的差是()。
A.0°B.45°C.60°D.90°2. 在图中,如点S、T分别在边AB的延长线上,且∠ASP=60°,∠BAT=20°,则∠AST为()。
A.40°B.50°C.80°D.110°3. 已知正方形ABCD的边长为5cm,点E、F分别在边AD、AB上,且AE=BF,则三角形CEF的面积为()。
A.(5/8) cm²B.(9/8) cm²C.(13/8) cm²D.(15/8) cm²4. 如果一个圆心角的度数为30°,则它所对的弧度数是()。
A.π/6B.π/3C.π/4D.π/2填空题:1.如图,已知BC平分∠ABD,设∠BAC=a°,∠BCA=b°,则∠CBD=\_\_\_\_°。
2.如图,点A、B、C在同一条直线上,则对于ΔABC来说,以下说法正确的是:①AB=AC;②\angleBAC是钝角;③\angleABC+\angleACB =180^\circ,所以\angleABC=\_\_\_\_°,\angleACB=\_\_\_\_°。
3. 已知直角三角形ABC,其中\angleC=90°,BC=3,AC=4,则AB=\_\_\_\_。
4.如图,长方形ABCD中,点E、F分别为BC、CD上的点,若∠BAE=∠EFD,AB=10cm,则DF=\_\_\_\_cm。
解答题:1.如图,在\triangleABC中,垂足分别为D、E、F。
若AC=6,BD=8,DE=5,EF=9,则BC=()。
2.如图,已知\angleBAC=60°,AD平分\angleBAC,且BD=AD,点E为AD的延长线上的点,且\angleBEC=140°,则\angleACD=\_\_\_\_\_\_°。
几何初二试题及答案

几何初二试题及答案一、选择题1. 已知一个三角形的两边长分别为3和4,第三边的长x满足的不等式是:A. 1 < x < 7B. 4 < x < 7C. 1 < x < 4D. 3 < x < 7答案:D2. 一个圆的半径为5cm,那么这个圆的周长是多少?A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案:D3. 已知一个矩形的长为6cm,宽为4cm,那么这个矩形的面积是多少?A. 20cm²B. 24cm²C. 18cm²D. 16cm²答案:B二、填空题1. 平行四边形的对角线互相______。
答案:平分2. 如果一个角的度数是30°,那么它的余角是______。
答案:60°3. 一个直角三角形的两条直角边分别为3和4,那么它的斜边长是______。
答案:5三、简答题1. 描述如何使用勾股定理来计算直角三角形的斜边长。
答案:首先确定直角三角形的两条直角边的长度,设为a和b。
根据勾股定理,斜边c的长度可以通过公式c = √(a² + b²) 来计算。
2. 解释什么是相似三角形,并给出一个例子。
答案:相似三角形是指两个三角形的对应角相等,对应边的比例相等的三角形。
例如,如果三角形ABC与三角形DEF的角A等于角D,角B等于角E,角C等于角F,并且边AB与边DE、边BC与边EF、边AC与边DF的长度比例相等,那么这两个三角形就是相似的。
四、解答题1. 已知一个等腰三角形的底边长为10cm,两腰的长度为13cm,求这个三角形的面积。
答案:首先,我们可以将等腰三角形分成两个直角三角形,通过底边的中点。
这样,每个直角三角形的底边长度为5cm,斜边为13cm。
根据勾股定理,我们可以计算出高h:h = √(13² - 5²) = √(169 - 25) = √144 = 12cm。
初中数学几何证明经典试题(含答案)
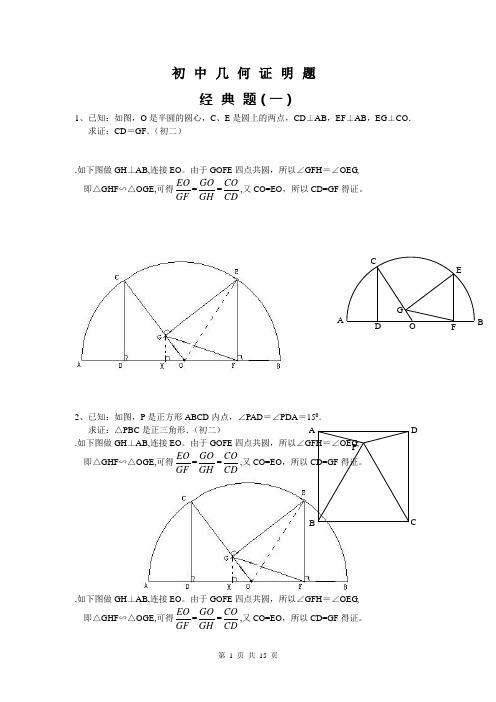
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初二几何试题及答案

初二几何试题及答案1. 已知三角形ABC中,AB=AC,D是BC边上的中点。
求证:AD垂直于BC。
答案:因为AB=AC,所以三角形ABC是等腰三角形。
根据等腰三角形的性质,底边的中线、高线和角平分线重合。
因此,AD既是BC边上的中线,也是高线,所以AD垂直于BC。
2. 一个矩形的长是宽的两倍,且对角线长为10cm。
求矩形的长和宽。
答案:设矩形的宽为x cm,则长为2x cm。
根据勾股定理,对角线的长度满足方程x^2 + (2x)^2 = 10^2。
解得x^2 + 4x^2 = 100,即5x^2 = 100,所以x^2 = 20,x = √20。
因此,矩形的宽为√20 cm,长为2√20 cm。
3. 一个圆的直径是10cm,求这个圆的面积。
答案:圆的面积公式为A = πr^2,其中r是圆的半径。
因为直径是10cm,所以半径r = 10/2 = 5cm。
代入公式得A = π * 5^2 = 25π cm^2。
4. 一个梯形的上底是8cm,下底是12cm,高是5cm。
求梯形的面积。
答案:梯形的面积公式为A = (a + b) * h / 2,其中a和b分别是上底和下底的长度,h是高。
代入数据得A = (8 + 12) * 5 / 2 = 20 * 5 / 2 = 50 cm^2。
5. 已知一个直角三角形的两条直角边分别是6cm和8cm,求斜边的长度。
答案:根据勾股定理,斜边的长度c满足方程c^2 = a^2 + b^2,其中a和b分别是两条直角边的长度。
代入数据得c^2 = 6^2 + 8^2 = 36+ 64 = 100,所以c = √100 = 10cm。
6. 一个正六边形的边长是4cm,求它的面积。
答案:正六边形可以被分成6个等边三角形,每个等边三角形的边长都是4cm。
等边三角形的面积公式为A = (√3 / 4) * a^2,其中a是边长。
因此,正六边形的面积为6 * (√3 / 4) * 4^2 = 6 * √3 * 4 = 24√3 cm^2。
八年级上册数学几何精典习题含答案

练习11.如图,等腰直角三角形BDC的顶点D在等边三角形ABC的内部,∠BDC=90°,连接AD,过点D作一条直线将△ABD分割成两个等腰三角形,则分割出的这两个等腰三角形的顶角度数分别是_________。
2.如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为()A.32B.64 C.128 D.2563.等腰三角形一腰上的高与另一腰的夹角为48°,则该等腰三角形的底角的度数为_______4.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有_______。
5.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.1.在平面直角坐标系中,点A在第一象限,点P在X 轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有_______个。
2.已知△ABC中,AB=6,AC=8,BC=11,任作一条直线将△ABC分成两个三角形,若其中有一个三角形是等腰三角形,则这样的直线最多有______条。
3.如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是_______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
八年级数学几何经典题【含答案】
1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长
线交MN 于E 、F .
求证:∠DEN =∠F .
2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,
点P 是EF 的中点.
求证:点P 到边AB 的距离等于AB 的一半.
3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .
求证:CE =CF .
.
4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .
求证:AE =AF .
B
5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .
求证:PA =PF .
6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .
7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EF
D F
E
P C
B A
F
P
D
E C
B
A
,
九年级数学【答案】
1.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=
2
EG
FH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
从而可得PQ=
2
AI BI
=
2
AB
,从而得证。
3.顺时针旋转△ADE ,到△ABG ,连接CG . 由于∠ABG=∠ADE=900+450=1350 从而可得B ,G ,D 在一条直线上,可得△AGB ≌△CGB 。
推出AE=AG=AC=GC ,可得△AGC 为等边三角形。
∠AGB=300,既得∠EAC=300,从而可得∠A EC=750。
又∠EFC=∠DFA=450+300=750. 可证:CE=CF 。
4.连接BD 作CH ⊥DE ,可得四边形CGDH 是正方形。
由AC=CE=2GC=2CH ,
可得∠CEH=300,所以∠CAE=∠CEA=∠AED=150,
又∠FAE=900+450+150=1500,
从而可知道∠F=150,从而得出AE=AF 。
5证明:(1)在AB 上取一点M ,使AM EC =,连接ME . BM BE ∴=.45BME ∴∠=°,135AME ∴∠=°. CF 是外角平分线,45DCF ∴∠=°,135ECF ∴∠=°. AME ECF ∴∠=∠. (2)
证明:在BA 的延长线上取一点N .使AN CE =,连接NE .
BN BE ∴=. 45N PCE ∴∠=∠=°. 四边形ABCD 是正方形, AD BE ∴∥. DAE BEA ∴∠=∠. NAE CEF ∴∠=∠.
ANE ECF ∴△≌△(ASA )
. AE EF ∴=.
6.过D 作AQ ⊥AE ,AG ⊥CF ,由ADE S
=
2
ABCD
S
=DFC
S
,可得:
2AE PQ =2
AE PQ
,由AE=FC 。
可得DQ=DG ,可得∠DPA =∠DPC (角平分线逆定理)。
A
D F C G
E B M A
D
G
E B
图3
A
D F
C G
E B N
7证明:过D作DG//AB交EA的延长线于G,可得∠DAG=30°∵∠BAD=30°+60°=90°
∴∠ADG=90°
∵∠DAG=30°=∠CAB,AD=AC
∴Rt△AGD≌Rt△ABC
∴AG=AB,∴AG=AE
∵DG//AB
∴EF//FD
8证明:作DA、CE的延长线交于H
∵ABCD是正方形,E是AB的中点
∴AE=BE,∠AEH=∠BEC
∠BEC=∠EAH=90°
∴△AEH ≌△BEC (ASA ) ∴AH=BC ,AD=AH 又∵F 是BC 的中点 ∴Rt △DFC ≌Rt △CEB ∴∠DFC=∠CEB
∴∠GCF +∠GFC=∠ECB +∠CEB=90° ∴∠CGF=90° ∴∠DGH=∠CGF=90° ∴△DGH 是Rt △ ∵AD=AH ∴AG=DH 2
1
=AD
9证明:如图,连接EC,取EC 的中点G,AE 的中点H ,连接DG,HG 则:GH=DG 所以:角1=∠2, 而∠1=∠4,∠2=∠3=∠5 所以;∠4=∠5 所以:AF=EF.。
