同底数幂的乘法测试题
初一数学有理数的加减乘除以及乘方试题答案及解析

初一数学有理数的加减乘除以及乘方试题答案及解析1.科学发现:植物的花瓣、萼片、果实的数目以及其他方面的特征,都非常吻合于一个奇特的数列——著名的裴波那契数列:1,1,2,3,5,8,13,21,34,55,……仔细观察以上数列,则它的第11个数应该是 .【答案】89.【解析】观察发现:从第三个数开始,后边的一个数总是前边两个数的和,则第11个数是34+55=89.试题解析:第11个数是34+55=89.【考点】规律型:数字的变化类.2.将正整数依次按下表规律排成4列,根据表中的排列规律,数2014应在( )A.第672行第1列B.第672行第4列C.第671行第1列D.第671行第4列【答案】B.【解析】每行有3列,奇数开始的从左边开始排列,偶数开始的从右边开始排列.每行的最后都是3的倍数.2014÷3=671……1,所以数2014应在第672行第4列.故选B.【考点】规律型:数字的变化类.3.已知在0摄氏度及一个标准大气压下1cm3空气的质量是0.001293克,数0.001293用科学计数法表示为__________ .【答案】.【解析】用科学记数法表示绝对值小于的数,只要将小数定向右移到第一个不为零的数后,若共移动位,则最后乘以即可,如本题中向右移了位,变为,在后乘以,最后.【考点】科学记数法.4.计算:= 。
【答案】.【解析】【考点】同底数幂的乘法.5.在一次水灾中,大约有个人无家可归,假如一顶帐篷占地100米,可以放置40个床位(一人一床位),为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约要占多少地方?若某广场面积为5000米2。
要安置这些人,大约需要多少个这样的广场?(所有结果用科学计数法表示)【答案】(1);(2);(3).【解析】根据帐篷的数量=总人数÷每一个帐篷所容纳的人数;所占面积=帐篷数×一顶帐篷所占的面积,计算即可.试题解析:根据题意得2.5×107÷40=625000=顶帐篷,625000×100=6.25×107米2,6.25×107÷5000=个.考点: 整式的除法.6.明近期几次数学测试成绩如下:第一次85分,第二次比第一次高8分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是()A.90分B.75分C.91分D.81分【答案】C【解析】小明第四次测验的成绩是故选C.7.下列各组的两个数中,运算后的结果相等的是()A.和B.和C.和D.和【答案】B【解析】A.,,故本选项错误;B.,,故本选项正确;C.,,故本选项错误;D.,,故本选项错误.故选B.8.若规定“!”是一种数学运算符号,且则的值为()A.B.99!C.9 900D.2!【答案】C【解析】根据题意可得:100!=100×99×98×97×...×1,98!=98×97× (1)∴=100×99="9" 900,故选C.9.若规定,则的值为 .【答案】【解析】.10.李强靠勤工俭学的收入维持上大学费用,表中是李强某一周的收支情况表,记收入为正,支出为负(单位:元):星期一二三四五六日(2)照这个情况估计,李强一个月(按30天计算)能有多少节余?(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?【答案】(1)到这个周末,李强有14元节余.(2)照这个情况估计,李强一个月(按30天计算)能有60元节余.(3)按以上的支出水平,李强一个月(按30天计算)至少有360元收入才能维持正常开支.【解析】分析:(1)七天的收入总和减去支出总和即可;(2)首先计算出平均一天的节余,然后乘30即可;(3)计算出这7天支出的平均数,即可作为一个月中每天的支出,乘30即可求得.解:(1)由题意可得:(元).(2)由题意得:14÷7×30=60(元).(3)根据题意得:10+14+13+8+10+14+15=84,84÷7×30=360(元).答:(1)到这个周末,李强有14元节余.(2)照这个情况估计,李强一个月(按30天计算)能有60元节余.(3)按以上的支出水平,李强一个月(按30天计算)至少有360元收入才能维持正常开支.11.有理数0.0050400的有效数字的个数是().A.3个B.4个C.5个D.6个【答案】C【解析】有效数字是从左边第一个不是0的数字起,后面所有的数字都是有效数字.解:有理数0.0050400的有效数字有5、0、4、0、0这5个,故选C.【考点】近似数和有效数字点评:本题是基础应用题,只需学生熟练掌握有效数字的定义,即可完成.12.计算:;【答案】-5【解析】先根据有理数的乘方法则计算,再根据有理数的乘法法则计算,最后算加减即可.解:原式.【考点】有理数的混合运算点评:计算题是中考必考题,一般难度不大,学生要特别慎重,尽量不在计算上失分.13.观察下列各式:31=3,32=9,33=27,34=81, 35=243,36=729…你能从中发现底数为3的幂的个位数有什么规律吗?根据你发现的规律回答:3的个位数字是。
七年级数学下册第八章《幂的运算》单元测试卷-苏科版(含答案)

七年级数学下册第八章《幂的运算》单元测试卷-苏科版(含答案)一.选择题(共7小题,满分21分)1.若a•2•23=26,则a等于()A.4B.8C.16D.322.已知a≠0,下列运算中正确的是()A.a2•a3=a6B.a5﹣a3=a2C.(﹣a3)2=a5D.a•a3=a43.若10m=5,10n=3,求102m﹣3n的值()A.B.C.675D.4.若(2x﹣1)0有意义,则x的取值范围是()A.x=﹣2B.x≠0C.x≠D.x=5.若(x﹣3)0﹣2(2x﹣4)﹣1有意义,则x取值范围是()A.x≠3B.x≠2C.x≠3且x≠﹣2D.x≠3且x≠2 6.“绿水青山就是金山银山”.某地积极响应党中央号召,大力推进农村厕所革命,已经累计投资1.102×108元资金.数据1.102×108用科学记数法可表示为()A.1102亿B.1.102亿C.110.2亿D.11.02亿7.嫦娥五号返回器携带月球样品安全着陆,标志着中国航天业向前又迈出了一大步.嫦娥五号返回器在接近大气层时,飞行1m大约需要0.0000893s.数据0.0000893s用科学记数法表示为()A.8.93×10﹣5B.893×10﹣4C.8.93×10﹣4D.8.93×10﹣7二.填空题(共7小题,满分21分)8.将2x﹣3y(x+y)﹣1表示成只含有正整数指数幂的形式为.9.新型冠状病毒直径约为100nm,计m(用科学记数法表示).10.若有意义,则x的取值范围是.11.若a2n=2(n为正整数),则(4a3n)2÷4a4n的值为.12.目前全国疫情防控形势依旧严峻,我们应该坚持“勤洗手,戴口罩,常通风”.一双没有洗过的手,带有各种细菌约7.5×105个,则科学记数法数据7.5×105的原数为.13.已知x2n=5,则(3x3n)2﹣4(x2)2n的值为.14.已知m x=2,m y=4,则m x+y=.三.解答题(共6小题,满分58分)15.计算:(1)2+(﹣2)×3+(﹣7)0;(2)×12.16.在数学中,我们经常会运用逆向思考的方法来解决一些问题,例如:“若a m=4,a m+n =20,求a n的值.”这道题我们可以这样思考:逆向运用同底数幂的乘法公式,即a m+n =a m•a n,所以20=4•a n,所以a n=5.(1)若a m=2,a2m+n=24,请你也利用逆向思考的方法求出a n的值.(2)下面是小贤用逆向思考的方法完成的一道作业题,请你参考小贤的方法解答下面的问题:小贤的作业计算:89×(﹣0.125)9.解:89×(﹣0.125)9=(﹣8×0.125)9=(﹣1)9=﹣1.①小贤的求解方法逆用了哪一条幂的运算性质,直接写出该逆向运用的公式:.②计算:52023×(﹣0.2)2022.17.(1)若3×27m÷9m=316,求m的值;(2)已知a x=﹣2,a y=3,求a3x﹣2y的值;(3)若n为正整数,且x2n=4,求(3x2n)2﹣4(x2)2n的值.18.我们知道,同底数幂的乘法法则为a m•a n=a m+n(其中a≠0,m、n为正整数),类似地,我们规定关于任意正整数m、n的一种新运算:f(m)•f(n)=f(m+n)(其中m、n为正整数).例如,若f(3)=2,则f(6)=f(3+3)=f(3)•f(3)=2×2=4.f(9)=f(3+3+3)=f(3)•f(3)•f(3)=2×2×2=8.(1)若f(2)=5,①填空:f(6)=;②当f(2n)=25,求n的值;(2)若f(a)=3,化简:f(a)•f(2a)•f(3a)•…•f(10a).19.如表是某河流今年某一周内的水位变化情况,上周末(星期六)的水位已经达到警戒水位33米.(正号表示水位比前一天上升,负号表示水位比前一天下降).(单位:米)星期日一二三四五六水位变化+0.2+0.8﹣0.4+0.2+0.3﹣0.5﹣0.2(1)本周哪一天河流的水位最高?哪一天河流的水位最低?分别是多少?(2)与上周末相比,本周末河流的水位是上升了还是下降了?本周末的水位是多少?(3)若水位每下降1厘米,就有2.5×102吨水蒸发到大气中,请计算这个星期共有多少吨水蒸发到大气中?20.已知10﹣2α=3,,求106α+2β的值.参考答案一.选择题(共7小题,满分21分)1.解:∵a•2•23=26,∴a=26÷24=22=4.故选:A.2.解:A、原式=a5,故不符合题意;B、a5与a3不是同类项,故不能合并,故不符合题意;C、原式=﹣a6,故不符合题意;D、原式=a4,故符合题意.故选:D.3.解:∵10m=5,10n=3,∴102m﹣3n=102m÷103n=.故选:D.4.解:(2x﹣1)0有意义,则2x﹣1≠0,解得:x≠.故选:C.5.解:若(x﹣3)0﹣2(2x﹣4)﹣1有意义,则x﹣3≠0且2x﹣4≠0,解得:x≠3且x≠2.故选:D.6.解:1.102×108=1.102亿.故选:B.7.解:0.0000893=8.93×10﹣5,故选:A.二.填空题(共7小题,满分21分)8.解:原式=•=.故答案为:.9.解:新型冠状病毒的直径约为100nm=100×10﹣9m=1×10﹣7m,故答案为1×10﹣7.10.解:∵有意义,∴0.∴x+2≠0,x﹣2≠0,∴x≠±2.故答案为:x≠±2.11.解:当a2n=2时,(4a3n)2÷4a4n=16(a2n)3÷4(a2n)2=16×23÷(4×22)=16×8÷(4×4)=16×8÷16=8.故答案为:8.12.解:7.5×105=750000,故答案为:750000.13.解:∵x2n=5,∴(3x3n)2﹣4(x2)2n=9x6n﹣4x4n=9(x2n)3﹣4(x2n)2=9×53﹣4×52=1125﹣100=1025.故答案为:1025.14.解:∵m x=2,m y=4,∴m x+y=m x•m y=8,故答案为:8.三.解答题(共6小题,满分58分)15.解:(1)原式=2﹣6+1=﹣3;(2)原式=×12+=5+8﹣1616.解:(1)∵a m=2,∴a2m+n=24,∴a2m×a n=24,(a m)2×a n=24,22×a n=24,∴4a n=24,∴a n=6;(2)①逆用积的乘方,其公式为:a n•b n=(ab)n,故答案为:a n•b n=(ab)n;②52023×(﹣0.2)2022=5×52022×(﹣0.2)2022=5×(﹣0.2×5)2022=5×(﹣1)2022=5×1=5.17.解:(1)∵3×27m÷9m=316,∴3×33m÷32m=316,∴33m+1﹣2m=316,∴3m﹣2m+1=16,解得m=15;(2)∵a x=﹣2,a y=3,∴a3x=﹣8,a2y=9,∴a3x﹣2y=a3x÷a2y=(﹣8)÷9=﹣;(3)∵x2n=4,∴(3x2n)2﹣4(x2)2n=(3x2n)2﹣4(x2n)2=(3×4)2﹣4×42=122﹣4×16=144﹣64=80.18.解:(1)①∵f(2)=5,∴f(6)=f(2+2+2)=f(2)•f(2)•f(2)=125;故答案为:125;②∵25=5×5=f(2)•f(2)=f(2+2),f(2n)=25,∴f(2n)=f(2+2),∴2n=4,∴n=2;(2)∵f(2a)=f(a+a)=f(a)•f(a)=3×3=31+1=32,f(3a)=f(a+a+a)=f(a)•f(a)•f(a)=3×3×3=31+1+1=33,…,f(10a)=310,∴f(a)•f(2a)•f(3a)•…•f(10a)=3×32×33×…×310=31+2+3+…+10=355.19.解:(1)周日:33+0.2=33.2(米),周一:33.2+0.8=34(米),周二:34﹣0.4=33.6(米),周三:33.6+0.2=33.8(米),周四:33.8+0.3=34.1(米),周五:34.1﹣0.5=33.6(米),周六:33.6﹣0.2=33.4(米).答:周四水位最高,最高水位是34.1米,周日水位最低,最低水位是33.2米;(2)33.4﹣33=0.4>0,答:与上周末相比,本周末河流的水位上升了,水位是33.4米;(3)100×(0.4+0.5+0.2)×2.5×102吨=2.75×104(吨),答:这个星期共有2.75×104吨水蒸发到大气中.20.解:∵10﹣2α==3,10﹣β==﹣,∴102α=,10β=﹣5,∴106α+2β=(102α)3•(10β)2,=()3×(﹣5)2,=×25,=.。
八年级数学同底数幂的乘法测试题

13.1.1 同底数幂的乘法教学目标:1.熟练运用同底数幂的乘法运算法则。
◆随堂检测1、判断1)x5·x5=2x5 ( )2)x13+x13=x26 ( )3)m·m3=m3 ( )4)x3(-x)4=-x7 ( )2、填空:1)54m m =2)n n y y y --∙∙533=3)()()32a a --=4)()()22x x --=3、计算:1)103×1042)(-2)2·(-2) 3·(-2)3)a·a 3·a 54)(a+b)(a+b)m (a+b)n5) a 4n a n+3a6)-a 2·a 37) (-a )2·a 3(8) ()()5222x y y x -∙-1.若 3m =5, 3n =7, 求3m+n+1的值分析:本题的切入点是同底数幂的乘法性质的逆用:a m+n =a m ·a n (m,n 为正整数)。
运用此法则,可以把一个幂分解成两个(或两个以上)同底数幂的积。
其中,拆分所得的(两个或两个以上)同底数幂的底数与原来幂的底数相同,指数之和等于原来幂的指数。
解:∵3m =5, 3n =7,∴3m+n+1=3m ·3n ·3=5×7×3=1051)()()()[]m n py x x y y x 32--∙-∙-= 2)已知2x+2=m,用含m 的代数式表示2x = _____(1)下列计算中 ①b 5+b 5=2b 5 ②b 5·b 5=b 10③y 3·y 4=y 12④m·m 3=m 4 ⑤m 3·m 4=2m 7其中正确的个数有( )A 1个B 2个C 3个D 4个(2)x 3m+2不等于( )A x 3m ·x 2B x m ·x2m+2 C x 3m +2 D x m+2·x 2m3、解答题:(1)5,35==+++b a c b a x x ,求c x 的值. (2)若,14x x x x n m =∙∙求m+n.(3)若61a aa n m n =∙++,且m-2n=1,求n m 的值. (4)计算:4353x x x x x ∙∙+∙.1.(2009年重庆市江津区)下列计算错误的是( ) A .2m+3n=5mnB .426a a a =÷C.632)(x x =D.32a a a =⋅ 2.下列计算中,结果正确的是( )A .236a a a =· B .()()26a a a =·3 C .()326a a = D .623a a a ÷=参考答案:随堂检测1、判断:本题考查同底数幂的乘法法则及合并同类项(1)×(2)×(3)×(4)×2、填空: (1)m 9 (2)y 5 (3)本题要注意符号错误 -a 5(4)注意符号 -x 43、计算:(1)107 (2)26 (3)a 9 ( 4)(a+b)m+n+1 (5)a5n+4 (6) -a 5 (7) a 5 (8)(2y-x)7 拓展提高1、填空;(1)()()()[]m n p y x x y y x 32--∙-∙-=-(x-y )p ·(x-y )2n ·(x-y )3m =-(x-y)p+2n+3m (2)2x+2=2x ·22=m,∴2x=4m2、选择:(1)A 本题考查同底数幂的乘法性质的运用(2)C 由同底数幂的乘法性质可知A、B、D运算结果均为x3m+2,故选 C 3、解答题(1) ∵x a+b+c=x a+b·x c=35,x a+b=5,∴cx=7(2) 由,14x x x x n m=∙∙得x1+m+n=x14,∴1+m+n=14,∴m+n=13 (3)∵a n+1·a m+n=a6∴n+1+m+n=6,即m+2n=5 ,又∵m-2n=1,∴m=3,n=1,∴m n =3(4) 4353x x x x x ∙∙+∙=x 8+x 8=2x8体验中考 1、幂的运算【答案】A2、解析:本题考查整式的有关运算,235a a a = ,选项A 是错的,()()226a a a =·3,选项B 是错的,()326a a =,选项C 是正确的,故选C。
幂的运算(3大知识点7类题型)(知识梳理与题型分类讲解)(人教版)(教师版)25学年八年级数学上册

专题14.1幂的运算(3大知识点7类题型)(知识梳理与题型分类讲解)第一部分【知识点归纳与题型目录】【知识点1】同底数幂的乘法法则+⋅=m n m n a a a (其中,m n 都是正整数).即同底数幂相乘,底数不变,指数相加.【要点提示】(1)同底数幂是指底数相同的幂,底数可以是任意的实数,也可以是单项式、多项式.(2)三个或三个以上同底数幂相乘时,也具有这一性质,即mnpm n pa a a a++⋅⋅=(,,m n p 都是正整数).(3)逆用公式:把一个幂分解成两个或多个同底数幂的积,其中它们的底数与原来的底数相同,它们的指数之和等于原来的幂的指数。
即m nm n aa a +=⋅(,m n 都是正整数).【知识点2】幂的乘方法则()=m n mn a a (其中,m n 都是正整数).即幂的乘方,底数不变,指数相乘.【要点提示】(1)公式的推广:(())=m n pmnpa a (0≠a ,,,m n p 均为正整数)(2)逆用公式:()()nmmnm n a aa ==,根据题目的需要常常逆用幂的乘方运算能将某些幂变形,从而解决问题.【知识点3】积的乘方法则()=⋅n n nab a b (其中n 是正整数).即积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.【要点提示】(1)公式的推广:()=⋅⋅nnnnabc a b c(n 为正整数).(2)逆用公式:()n n na b ab =逆用公式适当的变形可简化运算过程,尤其是遇到底数互为倒数时,计算更简便.如:1010101122 1.22⎛⎫⎛⎫⨯=⨯= ⎪ ⎪⎝⎭⎝⎭【知识点4】注意事项(1)底数可以是任意实数,也可以是单项式、多项式.(2)同底数幂的乘法时,只有当底数相同时,指数才可以相加.指数为1,计算时不要遗漏.(3)幂的乘方运算时,指数相乘,而同底数幂的乘法中是指数相加.(4)积的乘方运算时须注意,积的乘方要将每一个因式(特别是系数)都要分别乘方.(5)灵活地双向应用运算性质,使运算更加方便、简洁.(6)带有负号的幂的运算,要养成先化简符号的习惯.【题型目录】【题型1】同底数幂的乘法运算及逆运算...........................................2;【题型2】幂的乘方运算及逆运算.................................................4;【题型3】积的乘方运算及逆运算.................................................7;【题型4】幂的混合运算.........................................................9;【题型5】幂的运算的应用.......................................................11;【题型6】直通中考.............................................................13;【题型7】拓展与延伸...........................................................14.第二部分【题型展示与方法点拨】【题型1】同底数幂的乘法运算及逆运算【例1】(23-24七年级上·河南周口·期中)在学习第一章有理数时,类比小学两个正数的运算法则学习了有理数的加减法、有理数的乘除法,在第二章整式的加减时,类比第一章有理数的学习过程学习了整式的加减,那么整式的乘法是否可以类比有理数的乘法进行学习呢?我们从特殊情况入手对两个同底数幂相乘进行探究.(1)探究根据乘方的意义填空,观察计算结果,你能发现什么规律①53( )222⨯=,②42( )a a a ⋅=,③( )555m n ⨯=,(2)规律( )m n a a a ⋅=(,m n 都是正整数).即__________________________.(文字表达)(3)应用①计算31m m a a +⋅;②把(2)x y +看成一个整体,计算23(2)(2)x y x y +⋅+.【答案】(1)①8;②6;③;m n +(2);m n +同底数幂相乘,底数不变,指数相加(3)①41m a +;②5(2)x y +【分析】本题考查了同底数幂的乘法公式的推导和应用.掌握同底数幂的乘法公式的计算公式是关键;(1)(2)(3)根据同底数幂相乘,底数不变,指数相加解答即可;解:(1)①853(35)2222+⨯==,②642(4+2)a a a a ⋅==,③555m n m n +⨯=,故答案为:8;6;;m n +(2)m n m n a a a +⋅=,即同底数幂相乘,底数不变,指数相加;故答案为:;m n +同底数幂相乘,底数不变,指数相加;(3)①1314m m m a a a ++⋅=;②253.(2)(2)(2)x y x y x y +=+⋅+【变式1】(23-24七年级下·全国·单元测试)计算3()()x y y x -⋅-=()A .4()x y -B .4()x y --C .4)y x -(D .4()x y +【答案】B【分析】本题考查了同底数幂的乘法法则,把()x y -看作一个整体,利用同底数幂的乘法法则即可求解.解题的关键是熟练的掌握同底数幂的乘法法则.解:334()()()()()x y y x x y x y x y -⋅-=--⋅-=--,故选:B .【变式2】(23-24七年级下·全国·单元测试)已知1222162x x ⋅⋅=,则x =.【答案】4【分析】本题主要考查了同底数幂的乘法运算,根据同底数幂相乘,底数不变指数相加,将1222162x x ⋅⋅=变形为:241222x +=,从而得出2412x +=,再求出x 的值即可.解:42421622222x x x x x +⋅=⋅⋅⋅=,∵1222162x x ⋅⋅=,∴241222x +=,∴2412x +=,解得:4x =.故答案为:4.【例2】(2024七年级下·全国·专题练习)(1)已知23x =,求32x +的值;(2)若21464a +=,求a 的值.【答案】(1)24;(2)1a =【分析】本题考查的是同底数幂的乘法运算的逆运算,熟记运算法则是解本题的关键;(1)由33222x x +=⨯,再代入数据计算即可;(2)由21344a +=,再建立方程求解即可.解:(1)∵23x =,∴332238242x x +=⨯=⨯=;(2)∵21464a +=,∴21344a +=,∴213a +=,解得1a =.【变式1】(23-24七年级下·江苏淮安·期中)已知23x =,26y =,则2x y +的值是()A .12B .18C .36D .54【答案】B【分析】本题考查了同底数幂的乘法的逆用,根据同底数幂的乘法法则进行变形即可求解,解题的关键是熟练掌握同底数幂的乘法法则.解:由8232261x y x y +=⨯=⨯=,故选:B .【变式2】(2024七年级上·上海·专题练习)已知4222112x x +-⋅=,则x 的值为.【答案】3【分析】本题主要考查同底数幂的乘法运算以及提取公因式法分解因式,熟练并正确掌握相关运算法则是解题的关键.解:∵4222112x x +-⋅=,∴()13221112x +⨯-=,故142162x +==,解得:3x =故答案为:3.【题型2】幂的乘方运算及逆运算【例3】(21-22七年级上·上海·期末)计算:()()()3254652x x x x x x ⎡⎤⋅-⋅+-⋅+-⎣⎦.【答案】12x 【分析】先计算幂的乘方和同底数幂的乘法,再合并同类项即可.解:()()()3254652x x x x x x ⎡⎤⋅-⋅+-⋅+-⎣⎦121212x x x =-++12x =.【点拨】本题考查了整式的运算法则,解题的关键是熟记幂的乘方,同底数幂的乘法,合并同类项的知识.【变式1】(2022·江苏镇江·中考真题)下列运算中,结果正确的是()A .224325a a a +=B .3332a a a -=C .235a a a ⋅=D .()325a a =【答案】C【分析】根据合并同类项法则,同底数幂的乘法法则,幂的乘方法则逐项计算即可判断选择.解:222325a a a +=,故A 计算错误,不符合题意;3332a a a -=-,故B 计算错误,不符合题意;235a a a ⋅=,故C 计算正确,符合题意;()326a a =,故D 计算错误,不符合题意.故选C .【点拨】本题考查合并同类项,同底数幂的乘法,幂的乘方.熟练掌握各运算法则是解题关键.【变式2】.若25 3 0x y +-=,则432⋅=x y .【答案】8【分析】根据已知条件可得2+5=3x y ,根据幂的乘方运算以及同底数幂的乘法进行计算即可求解.解:∵25 3 0x y +-=∴2+5=3x y ,∴432⋅=x y 2525322228x y x y +⨯===,故答案为:8.【点拨】本题考查了幂的乘方运算以及同底数幂的乘法,熟练掌握幂的运算法则是解题的关键.【例4】(2023八年级上·全国·专题练习)(1)若23m n a a ==,,求32m n a +的值;(2)若2639273x x ⨯⨯=,求x 的值.【答案】(1)72;(2)5【分析】(1)利用幂的乘方和同底数幂的乘法法则进行变形,再利用整体代入计算即可;(2)把2639273x x ⨯⨯=变形为1232633x x ++=,得到关于x 的方程,解方程即可得到答案;熟练掌握幂的乘方、同底数幂的乘法法则,并利用整体思想是解题的关键.解:(1)∵23m n a a ==,,∴32m na +32m na a =⋅()()32m na a =⋅3223=⨯89=⨯72=;(2)2639273x x ⨯⨯=,23263333x x=⨯⨯()(),23263333x x ⨯=⨯,1232633x x ++=,12326x x ++=,5x =.【变式1】已知553a =,444b =,335c =,则a 、b 、c 的大小关系为()A .c a b <<B .c b a<<C .a b c<<D .a c b<<【答案】A【分析】把a 、b 、c 三个数变成指数相同的幂,通过底数可得出a 、b 、c 的大小关系.解:∵a =(35)11=24311,b =(44)11=25611,c =(53)11=12511,又∵125243256<<,∴c a b <<.故选:A .【点拨】本题考查了幂的乘方的逆运算,解答本题关键是掌握幂的乘方法则,把各数的指数变成相同.【变式2】(23-24八年级上·重庆九龙坡·阶段练习)已知433,33a b ==,则239a b ⨯=.【答案】16【分析】直接根据同底数幂的乘法以及幂的乘方运算法则进行计算即可得到答案.解:∵433,33a b==,∴()()()()222222243933333163a b a ba b ⎛⎫⨯=⨯=⨯=⨯= ⎪⎝⎭故答案为:16.【点拨】本题主要考查了同底数幂的乘法以及幂的乘方,熟练掌握运算法则是解答本题的关键.【题型3】积的乘方运算及逆运算25.【例5】(22-23八年级上·黑龙江哈尔滨·阶段练习)(1)()34222x x x ⋅-;(2)()()23332232x y x y +-【答案】(1)6x ;(2)66x y 【分析】(1)根据同底数幂乘法法则及幂的乘方计算法则计算,再合并同类项即可;(2)根据积的乘方计算法则去括号,再合并同类项即可.解:(1)()34222x x x ⋅-662x x =-6x =;(2)()()23332232x y x y +-666698x y x y =-66x y =.【点拨】此题考查了整式的计算,正确掌握同底数幂乘法法则及幂的乘方计算法则、积的乘方计算法则、合并同类项法则是解题的关键.【变式1】(2022·广东深圳·中考真题)下列运算正确的是()A .268a a a ⋅=B .()3326a a -=C .()22a b a b+=+D .235a b ab+=【答案】A【分析】分别根据同底数幂的乘法法则,积的乘方运算法则,单项式乘多项式及合并同类项的法则逐一判断即可.解:A 、268a a a ⋅=,计算正确,故此选项符合题意;B 、33(2)8a a -=-,原计算错误,故此选项不符合题意;C 、2()22a b a b +=+,原计算错误,故此选项不符合题意;D 、23a b +,不是同类项不能合并,原计算错误,故此选项不符合题意.故选:A .【点拨】本题考查了同底数幂的乘法,合并同类项以及幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.【变式2】(20-21七年级下·江苏扬州·期末)已知am =10,bm =2,则(ab )m =.【答案】20【分析】根据积的乘方计算法则解答.解:∵am =10,bm =2,∴(ab )m =10220m m a b ⋅=⨯=,故答案为:20.【点拨】此题考查积的乘方计算法则:积的乘方等于积中每个因式分别乘方,再把结果相乘,熟记法则是解题的关键.【例6】(2023九年级·全国·专题练习)用简便方法计算:(1)88552510.25(4)57⎛⎫⎛⎫-⨯⨯⨯- ⎪ ⎪⎝⎭⎝⎭;(2)()201720180.1258⨯-.【答案】(1)1-;(2)8-.【分析】(1)原式逆用积的乘方运算法则进行计算即可;(2)先将20188-变形为201788-⨯,再逆用积的乘方运算法则进行计算即可.解:(1)88552510.25(4)57⎛⎫⎛⎫-⨯⨯⨯- ⎪ ⎪⎝⎭⎝⎭8585715()()()(4)547=-⨯⨯⨯-8855751(4)574⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=-⨯⨯⨯-⎢⎥⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦58751(4)574⎛⎫⎡⎤=-⨯⨯⨯- ⎪⎢⎥⎝⎭⎣⎦1(1)=⨯-1=-;(2)()201720180.1258⨯-()201720171888⎛⎫=⨯-⨯ ⎪⎝⎭()201720171888⎛⎫=⨯-⨯ ⎪⎝⎭20171888⎛⎫=-⨯⨯ ⎪⎝⎭18=-⨯8=-.【点拨】本题主要考查了积的乘方的逆运算,熟练掌握运算法则是解答本题的关键.【变式1】(22-23七年级下·河北沧州·期中)若n 为正整数.且24n a =,则()()223224nn a a -的值为()A .4B .16C .64D .192【答案】D【分析】根据积的乘方以及逆运算对式子进行化简求解即可.解:()()2232642444nnn na a a a -=-()()322232444444nna a =-=⨯-⨯()32444448192=⨯-=⨯=,故选D .【点拨】此题考查了幂的有关运算,解题的关键是熟练掌握幂的有关运算法则.同底数幂相乘(除),底数不变,指数相加(减);幂的乘方,底数不变,指数相乘;积的乘方,把每个因式分别乘方.【变式2】已知2232336x x x ++-⋅=,则x =.【答案】8.【分析】根据积的乘方和幂的乘方的逆运算,把等式变形,根据指数相同求解即可.解:2232336x x x ++-⋅=,根据积的乘方和幂的乘方,等式可变形为:223(23)(6)x x +-⨯=,即22666x x +-=,226x x +=-,解得,8x =故答案为:8.【点拨】本题考查了幂的运算的逆运算,解题关键是把等式恰当变形,依据底数相同,指数也相同列方程.【题型4】幂的混合运算【例7】(21-22八年级上·全国·课后作业)计算:(1)()()()2243224249()(2)--+-a a b a b ;(2)()()()22112()3------n n n nx x x x x .【答案】(1)8425a b ;(2)31n x -.【分析】(1)先计算幂的乘方,再计算同底数幂,最后合并同类项即可;(3)先计算幂的乘方,再计算同底数幂,最后合并同类项即可.解:(1)()()()2243224249()(2)--+-a a b a b ,=62484916a a b a b ⋅⋅+,=8484916a b a b +,=8425a b ;(2)()()()22112()3------n n n nx x x x x ,=()()21212()3n n n n xx x x x -----,=()2112123n n n n x x -+++--+,=313123n n x x ---+,=31n x -.【点拨】本题考查整式的幂指数运算,掌握幂的乘方,同底数幂的乘法,合并同类项是解题关键.【变式1】(20-21七年级下·甘肃兰州·阶段练习)下列各式计算正确的是()A .-3xy ·(-2xy )2=12x 3y 3B .4x 2·(-2x 3)2=16x 12C .(-a 2)·a 3=a 6D .2a 2b ·(-ab )2=2a 4b 3【答案】D【分析】根据幂的运算法则逐一计算,可得结果.解:A 、()2333212xy xy x y -⋅--=,故选项错误;B 、()22384216x x x ⋅-=,故选项错误;C 、()236a a a -⋅=-,故选项错误;D 、()224322a b ab a b ⋅-=,故选项正确;故选D .【点拨】本题考查了幂的混合运算,熟练掌握运算法则是解题的关键.【变式2】已知2,3x x a t ==,则24x =.(用含,a t 的代数式表示)【答案】3a t解:∵2x =a ,3x =t ,∴24x =(23×3)x =23x ×3x =(2x )3×3x =a 3t .故答案为a 3t .【题型5】幂的运算的应用【例8】(23-24八年级上·山西长治·阶段练习)我们知道,一般的数学公式、法则、定义可以正向运用,也可以逆向运用.对于“同底数幂的乘法”“幂的乘方”“积的乘方”这几个法则的逆向运用表现为m n m n a a a += ,()()n m mn m n a a a ==,()mm m a b ab =;(m ,n 为正整数).请运用这个思路和幂的运算法则解决下列问题:(1)已知552a =,443b =,334c =,请把a ,b ,c 用“<”连接起来:;(2)若2a x =,3b x =,求32a b x +的值;(3)计算:2001001011284⎛⎫⨯⨯ ⎪⎝⎭.【答案】(1)a c b <<;(2)72;(3)8.【分析】(1)根据逆用幂的乘方,化成指数相同的幂,再比较大小;(2)根据逆用同底数幂的乘法和逆用幂的乘方即可求解;(3)根据逆用同底数幂的乘法和逆用幂的乘方,化成指数相同的幂,再计算即可求解;本题主要考查了同底数幂的乘法、幂的乘方法则,掌握法则的逆用是解题的关键.(1)解:∵()11555112232a ===,()11444113381b ===,()11333114464c ===.又∵326481<<,∴a c b <<,故答案为:a c b <<;(2)解:32a bx +32a b x x =⋅,()()32a b x x =⋅,∵2a x =,3b x =,∴原式3223=⋅,89=⨯,72=;(3)解:2001001011284⎛⎫⨯⨯ ⎪⎝⎭()200210110031222⎡⎤⎛⎫=⨯⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,4001003031222⎛⎫=⨯⨯ ⎪⎝⎭,400403122⎛⎫=⨯ ⎪⎝⎭,40040031222⎛⎫=⨯⨯ ⎪⎝⎭,40031222⎛⎫=⨯⨯ ⎪⎝⎭,402312=⨯,8=.【变式1】(21-22八年级上·河南三门峡·期末)下列运算中,错误的个数是()(1)224a a a +=;(2)236a a a ⋅=;(3)2n n n a a a ⋅=;(4)()448a a a --⋅=A .1个B .2个C .3个D .4个【答案】D 【分析】利用同底数幂的乘法运算法则,合并同类项的法则对各式进行运算,即可得出结果.解:(1)22242a a a a ≠+=,故(1)错误;(2)2356a a a a ⋅≠=,故(2)错误;(3)22n n n n a a a a ⋅≠=,故(3)错误;(4)()4488a a a a ---⋅≠=,故(4)错误,综上所述,错误的个数为4个,故选:D .【点拨】本题主要考查同底数幂的乘法运算法则、合并同类项运算等知识,解题的关键是对相应的运算法【变式2】(20-21九年级下·湖南永州·期中)将边长为1的正方形纸片按如图所示方法进行对折,记第1次对折后得到的图形面积为S 1,第2次对折后得到的图形面积为S 2,…,第n 次对折后得到的图形面积为S n ,请根据图2化简,12320202021S S S S S +++++= .【答案】202111()2-【分析】先具体计算出S 1,S 2,S 3,S 4的值,得出面积规律,表示S 2021,再设12320202021S S S S S S =+++++ ①,两边都乘以12,得到42320212022111111((()()+()222222S =++++ ②,利用①−②,求解S ,从而可得答案.解:∵42320211234202111111111,(,(),(),(242821622S S S S S ======== 设S =42320211234202111111()()((22222S S S S S +++++=+++++ ①12320202021111111222222S S S S S S ∴=+++++ 4232021202211111(()()()+()22222=++++ ②①-②得,2022111()222S ∴=-202111()2S ∴=-故答案为:202111()2-.【点拨】本题考查的是图形的面积规律的探究,有理数的乘方运算的灵活应用,同底数幂的乘法与除法的应用,方程思想的应用,正方形的性质,掌握以上知识是解题的关键.第三部分【中考链接与拓展延伸】【题型6】直通中考【例9】(2024·河北·中考真题)若a ,b 是正整数,且满足8282222222a b a a a b b b ++⋅⋅⋅+=⨯⨯⋅⋅⋅⨯ 个相加个相乘,则a 与b 的关系正确的是()A .38a b +=B .38a b =C .83a b +=D .38a b=+【分析】本题考查了同底数幂的乘法,幂的乘方的运算的应用,熟练掌握知识点是解题的关键.由题意得:()8822a b ⨯=,利用同底数幂的乘法,幂的乘方化简即可.解:由题意得:()8822a b ⨯=,∴38222a b ⨯=,∴38a b +=,故选:A .【例10】(2024·山东烟台·中考真题)下列运算结果为6a 的是()A .23a a ⋅B .122a a ÷C .33a a +D .()32a 【答案】D【分析】本题考查了同底数幂的乘法,同底数幂的除法,合并同类项,幂的乘方,解题的关键是熟练掌握以上运算法则;根据同底数幂的乘法同底数幂的除法,合并同类项,幂的乘方,运算法则计算即可解:A .23235a a a a +⋅==,故选项不符合题意;B .12212210a a a a -÷==,故选项不符合题意;C .3332a a a +=,故选项不符合题意;D .()32236a a a ⨯==,故选项符合题意;故选:D .【题型7】拓展延伸【例11】(2024·河北·中考真题)“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示13223⨯,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,正确的是()A .“20”左边的数是16B .“20”右边的“□”表示5C .运算结果小于6000D .运算结果可以表示为41001025a +【答案】D 【分析】本题考查了整式的加法运算,整式的乘法运算,理解题意,正确的逻辑推理时解决本题的关键.设一个三位数与一个两位数分别为10010x y z ++和10m n +,则20,5,2,mz nz ny nx a ====,即4=m n ,可确定1,2n y ==时,则4,5,m z x a ===,由题意可判断A 、B 选项,根据题意可得运算结果可以表示为:()1000411002541001025a a a +++=+,故可判断C 、D 选项.解:设一个三位数与一个两位数分别为10010x y z ++和10m n+如图:则由题意得:20,5,2,mz nz ny nx a ====,∴4mz nz=,即4=m n ,∴当2,1n y ==时, 2.5z =不是正整数,不符合题意,故舍;当1,2n y ==时,则4,5,m z x a ===,如图:,∴A 、“20”左边的数是248⨯=,故本选项不符合题意;B 、“20”右边的“□”表示4,故本选项不符合题意;∴a 上面的数应为4a ,如图:∴运算结果可以表示为:()1000411002541001025a a a +++=+,∴D 选项符合题意,当2a =时,计算的结果大于6000,故C 选项不符合题意,故选:D .【例12】(19-20七年级下·江苏南京·期中)观察等式(2a ﹣1)a +2=1,其中a 的取值可能是()A .﹣2B .1或﹣2C .0或1D .1或﹣2或0【答案】D 【分析】存在3种情况:一种是指数为0,底数不为0;第二种是底数为1,指数为任意值;第三种是底数为-1,指数为偶数,分别求解可得.解:情况一:指数为0,底数不为0即:a +2=0,2a -1≠0解得:a =-2情况二:底数为1,指数为任意值即:2a -1=1解得:a =1情况三:底数为-1,指数为偶数即:2a -1=-1,解得a =0代入a +2=2,为偶数,成立故答案为:D【点拨】本题考查0指数和底数为±1的指数的特点,本题底数为-1的情况容易遗漏,需要关注.。
2024年福建莆田中考数学试题及答案(1)
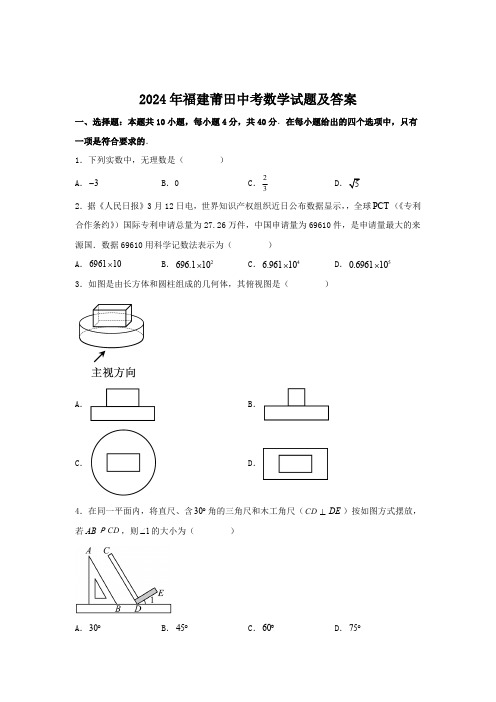
2024年福建莆田中考数学试题及答案一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.1.下列实数中,无理数是( )A .3-B .0C .23D 2.据《人民日报》3月12日电,世界知识产权组织近日公布数据显示,,全球PCT (《专利合作条约》)国际专利申请总量为27.26万件,中国申请量为69610件,是申请量最大的来源国.数据69610用科学记数法表示为( )A .696110´B .2696.110´C .46.96110´D .50.696110´3.如图是由长方体和圆柱组成的几何体,其俯视图是( )A .B .C .D .4.在同一平面内,将直尺、含30°角的三角尺和木工角尺(CD ^DE )按如图方式摆放,若AB P CD ,则1Ð的大小为( )A .30°B .45°C .60°D .75°5.下列运算正确的是( )A .339a a a ×=B .422a a a ¸=C .()235a a =D .2222a a -=6.哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想,我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.在质数2,3,5中,随机选取两个不同的数,其和是偶数的概率是( )A .14B .13C .12D .237.如图,已知点,A B 在O e 上,72AOB Ð=°,直线MN 与O e 相切,切点为C ,且C 为»AB 的中点,则ACM Ð等于( )A .18°B .30°C .36°D .72°8.今年我国国民经济开局良好,市场销售稳定增长,社会消费增长较快,第一季度社会消费品零售总额120327亿元,比去年第一季度增长4.7%,求去年第一季度社会消费品零售总额.若将去年第一季度社会消费品零售总额设为x 亿元,则符合题意的方程是( )A .()1 4.7%120327x +=B .()1 4.7%120327x -=C .1203271 4.7%x=+D .1203271 4.7%x=-9.小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案.如图,其中OAB V 与ODC V 都是等腰三角形,且它们关于直线l 对称,点E ,F 分别是底边AB ,CD 的中点,OE OF ^.下列推断错误的是( )A .OB OD ^B .BOC AOBÐ=ÐC .OE OF =D .180BOC AOD Ð+Ð=°10.已知二次函数()220y x ax a a =-+¹的图象经过1,2a A y æöç÷èø,()23,B a y 两点,则下列判断正确的是( )A .可以找到一个实数a ,使得1y a >B .无论实数a 取什么值,都有1y a >C .可以找到一个实数a ,使得20y <D .无论实数a 取什么值,都有20y <二、填空题:本题共6小题,每小题4分,共24分.11.因式分解:x 2+x = .12.不等式321x -<的解集是 .13.学校为了解学生的安全防范意识,随机抽取了12名学生进行相关知识测试,将测试成绩整理得到如图所示的条形统计图,则这12名学生测试成绩的中位数是 .(单位:分)14.如图,正方形ABCD 的面积为4,点E ,F ,G ,H 分别为边AB ,BC ,CD ,AD 的中点,则四边形EFGH 的面积为 .15.如图,在平面直角坐标系xOy 中,反比例函数ky x=的图象与O e 交于,A B 两点,且点,A B 都在第一象限.若()1,2A ,则点B 的坐标为 .16.无动力帆船是借助风力前行的.下图是帆船借助风力航行的平面示意图,已知帆船航行方向与风向所在直线的夹角PDA Ð为70°,帆与航行方向的夹角PDQ Ð为30°,风对帆的作用力F 为400N .根据物理知识,F 可以分解为两个力1F 与2F ,其中与帆平行的力1F 不起作用,与帆垂直的力2F 仪可以分解为两个力1f 与21,f f 与航行方向垂直,被舵的阻力抵消;2f 与航行方向一致,是真正推动帆船前行的动力.在物理学上常用线段的长度表示力的大小,据此,建立数学模型:400F AD ==,则2f CD == .(单位:N )(参考数据:sin400.64,cos400.77°=°=)三、解答题:本题共9小题,共86分。
第8章 幂的运算(能力提升)-2020-2021学年七年级数学下册单元测试(苏科版)(解析版)

2020-2021学年七年级数学下册《单元测试定心卷》(苏科版)第8章 幂的运算(能力提升卷卷)班级___________ 姓名___________ 学号____________ 分数____________考试范围:全章; 考试时间:120分钟; 总分:120分一、选择题(本大题共6小题,每小题2分,共12分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.(2021·广西玉林市·八年级期末)计算:a •a 2的结果是( )A .3aB .a 3C .2a 2D .2a 3【答案】B【分析】原式利用同底数幂的乘法法则计算即可得到结果.【详解】解:原式=a 3,故选:B .【点睛】此题考查了同底数幂的乘法,熟练掌握运算法则是解本题的关键.2.(2021·靖江外国语学校九年级月考)计算23(2)a b -的结果是( )A .636a b -B .28a b -C .632a b -D .638a b - 【答案】D【分析】根据积的乘方法则进行计算即可;【详解】 ()326328a b a b -=- , 故选:D .【点睛】本题考查了对积的乘方法则的应用,注意:积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘. 3.(2021·安徽九年级专题练习)下列运算结果为a 6的是( )A .a 2+a 3B .a 2•a 3C .(-a 2)3D .a 8÷a 2【答案】D【分析】根据合并同类项、同底数幂的乘除法以及积的乘方和幂的乘方进行计算即可.【详解】解:A 、a 3+a 2不能合并,故A 不符合题意;B 、a 2•a 3=a 5,故B 不符合题意;C 、(﹣a 2•)3=﹣a 6,故C 不符合题意;D 、a 8÷a 2=a 6,故D 符合题意;故选D .【点睛】本题考查了同底数幂的乘除法、合并同类项以及积的乘方和幂的乘方,解题关键是熟练掌握运算法则并能准确进行计算.4.(2021·山东枣庄市·九年级一模)下列运算正确的是( )A .236a a a =B .632a a a ÷=C .352()a a =D .2224()a b a b =【答案】D【分析】根据幂的运算法则逐项计算,然后判断正误即可.【详解】解:A . 235a a a =,原选项错误,不符合题意;B . 633a a a ÷=,原选项错误,不符合题意;C . 236()a a =,原选项错误,不符合题意;D . 2224()a b a b =,原选项正确,符合题意;故选:D .【点睛】本题考查了幂的运算,解题关键是熟知幂的运算法则,准确依据法则计算.5.(2021·山东省青岛实验初级中学九年级其他模拟)纳米技术,是研究结构尺寸在1至100纳米范围内材料的性质和应用.有一种纳米材料其理论厚度是0.00000000069m ,这个数用科学记数法表示正确的是( )A .100.6910-⨯B .90.6910-⨯C .96.910-⨯D .106.910-⨯【答案】D【分析】 科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】解:0.00000000069=6.9×10-10.故选:D .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.6.(2021·全国七年级专题练习)已知=2m x ,=3n x ,2m n x +=( )A .12B .108C .18D .36 【答案】A【分析】根据幂的乘方以及积的乘方的逆运算即可求出答案.【详解】∵=2m x ,=3n x ,∵()2222234312m n m n mn x x x x x +=⋅=⋅=⨯=⨯= 故选:A【点睛】本题考查学生的计算能力,解题的关键是熟练运用幂的乘方以及积的乘方的逆运算m n m n a a a +=⋅,()()n m mn n m a a a ==.二、填空题(本大题共10小题,每小题2分,共20分)7.(2021·全国九年级专题练习)53a a ÷=________.【答案】2.a【分析】利用同底数幂的除法法则:底数不变,指数相减,从而可得答案.【详解】解:53532,a a aa -÷== 故答案为:2.a【点睛】本题考查的是同底数幂的除法运算,掌握同底数幂的除法运算的运算法则是解题的关键.8.(2021·上海九年级专题练习)计算:62()a a -=________.【答案】8a【分析】先确定积的符号,再按照同底数幂的乘法法则运算即可得到答案.【详解】解:()62628a a a a a -=-•=-. 故答案为:8a .【点睛】本题考查的是同底数幂的乘法,掌握同底数幂的乘法法则是解题的关键.9.(2021·山西吕梁市·八年级期末)计算:202120201(2)()2-⋅-=_________. 【答案】-2【分析】先化成同底数幂,再根据同底数幂的乘法法则,即可求解.【详解】原式=202120201(2)()2-⋅- =20212020(2)(2)--⋅-=20212020(2)--=2-,故答案是:-2.【点睛】本题主要考查同底数幂的乘法,熟练掌握同底数幂的乘法法则,是解题的关键.10.(2021·全国七年级专题练习)如果a 3m +n =27,a m =3,则a n =_____.【答案】1【分析】根据幂的乘方和同底数幂的乘法运算法则,即可求解.【详解】∵a 3m +n =27,∵a 3m ·a n =27,∵(a m )3·a n =27,∵a m =3,∵33· a n =27,∵a n =1.故答案是:1.【点睛】本题主要考查幂的乘方和同底数幂的乘法法则,熟练掌握上述运算法则的逆运用,是解题的关键. 11.(2021·全国八年级)已知231682m ⨯=,则m =________.【答案】17【分析】先把23168⨯化为172,再根据指数相等求出m 的值.【详解】2342338917168(2)(2)2222m ⨯=⨯=⨯==.故17m =.故答案为:17【点睛】本题主要考查了幂的乘方与同底数幂的乘法,解题个关键是把23168⨯化为172.12.(2021·广东韶关市·八年级期末)已知340m n +-=,则28m n ⋅的值为_________.【答案】16【分析】用n 表示出m ,得43m n =-,将m 代入到28m n ⋅即可求解.【详解】解:∵340m n +-=,∵43m n =-,34334222216282m n n n m n -===∴⋅=.故答案为:16【点睛】本题考查了求代数式的值,同底数幂的乘法,正理解同底幂的乘法法则是解题的关键.13.(2021·河南商丘市·八年级期末)在学习了负整数指数幂的知识后,小明和小军两同学做了一个数学游戏,小明出了题目:将()()24252*2m n m n --⋅-的结果化为只含有正整数指数幂的形式,其结果为2416n m,则“*”处的数是多少?聪明的你替小军填上“*”处的数是___________.【答案】3-【分析】先用负整数指数幂将()()24252*2m n m n --⋅-化简为()22452*12m n m n ⎛⎫⋅ ⎪⎝⎭-,再结合积的乘方、幂的乘方解题即可.【详解】解:()()24252*2m nm n --⋅- ()22452*1=2m n m n ⎛⎫⋅ ⎪⎝⎭- 4*410481=2m n m n⋅ 444*+101=2m n由题意得,44*14+01=2m n 2416n m 4*+102=1n n ∴(4*+120)=n n -(4*+10)=2∴-4*12=-*3∴=-故答案为:3-.【点睛】本题考查负整数指数幂、幂的乘方、积的乘方等知识,是重要考点,难度较易,掌握相关知识是解题关键.14.(2021·内蒙古呼和浩特市·八年级期末)下列计算:①3100.0001-=;②()00.00011=;③()()352x x x --÷-=-;④22133a a -=;⑤()()321m m m m a a a -÷=-.其中运算正确的有______.(填序号即可) 【答案】②⑤.【分析】根据负整数指数幂、零指数幂、同底数幂的除法法则进行计算,逐个判断即可.【详解】 解:3110=0.0011000-=;故①计算错误; ()00.00011=;②计算正确; ()()22352()1x x x x x --=-÷=-=-;故③计算错误; 2233a a-=;故④计算错误 ()()333221(1)=(1)mm m m m m m m a a a a a a -÷=-⨯÷=--,故⑤计算正确 故答案为:②⑤.【点睛】本题考查同底数幂的除法,积的乘方以及零指数幂,负整数指数幂的计算,掌握运算法则正确计算是解题关键.15.(2021·上海九年级专题练习)观察等式:232222+=-;23422222++=-;2345222222+++=-…,若设502a =,则用含a 的式子表示5051529910022222+++++的结果是________.【答案】22a a -【分析】由等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2,得出规律:2+22+23+…+2n =2n +1-2,那么250+251+252+…+299+2100=(2+22+23+…+2100)-(2+22+23+…+249),将规律代入计算即可.【详解】∵2+22=23-2;2+22+23=24-2;2+22+23+24=25-2;…∵2+22+23+…+2n =2n +1-2,∵250+251+252+…+299+2100=(2+22+23+...+2100)-(2+22+23+ (249)=(2101-2)-(250-2)=2101-250,∵250=a ,∵2101=(250)2•2=22a ,∵原式=22a a -.故答案为:22a a -.【点睛】本题考查规律型问题:数字变化,列代数式,积的乘方等知识,解题的关键是通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.解决本题的难点在于得出规律:2+22+23+…+2n =2n +1-2. 16.(2021·四川成都市·八年级期中)我们规定一个新数“i ”,使其满足i 1=i ,i 2=﹣1,并且进一步规定:一切有理数可以与新数进行四则运算,且原有的运算律和运算法则仍然成立,于是有i 1=i ,i 2=﹣1,i 3=i 2•i =﹣i ,i 4=i 2•i 2=﹣1×(﹣1)=1.那么i 6=____,i 1+i 2+i 3+…+i 2022+i 2023=____.【答案】-1 -1【分析】各式利用题中的新定义计算即可求出值.【详解】解:i 6=i 5•i =-1,由题意得,i 1=i ,i 2=﹣1,i 3=i 2•i =﹣i ,i 4=i 2•i 2=﹣1×(﹣1)=1,i 5=i 4•i =i ,i 6=i 5•i =-1,故可发现4次一循环,一个循环内的和为0,2023÷4=505 (3)i 1+i 2+i 3+…+i 2022+i 2023=505×0+(i -1-i )=-1.故答案为:-1,-1.【点睛】本题考查了同底数幂的乘法运算,解答本题的关键是计算出前面几个数的值,发现规律,求出一个循环内的和再计算,有一定难度.三、解答题(本大题共11小题,17,18每小题7分,19,20,21,22,23,24,25每小题8分,26,27每小题9分,共88分.解答应写出文字说明、证明过程或演算步骤)17.(2020·四川省成都市玉林中学七年级月考)计算题.(1)()2432a a ⋅. (2)()()()2322252x xy x y ⋅-÷-. 【答案】(1)114a ;(2)10-.【分析】(1)先计算积得乘方,再按单项式的乘法法则运算即可;(2)先计算积得乘方,再按单项式的乘除法则运算即可.【详解】(1)原式834a a =⋅114a =.(2)原式()()3242854x xyx y =⋅-÷()()4242404x y x y =-÷10=-. 【点睛】本题考查了整式的混合运算,熟练掌握运算法则是解答本题的关键.18.(2019·扬州市邗江区实验学校七年级月考)计算:(1)﹣b 2×(﹣b )2×(﹣b 3); (2)(x ﹣y )3×(y ﹣2)2×(y ﹣2)5【答案】(1)b 7;(2)(x ﹣y )3(y ﹣2)7.【分析】(1)直接利用同底数幂的乘法运算法则进而计算得出答案;(2)直接利用同底数幂的乘法运算法则进而计算得出答案.【详解】解:(1)﹣b 2×(﹣b )2×(﹣b 3)=b 2×b 2×b 3=b 7;(2)(x ﹣y )3×(y ﹣2)2×(y ﹣2)5=(x ﹣y )3(y ﹣2)7.【点睛】本题考查幂的相关计算,有时候需要有整体思想,把底数可以为多项式的.19.(2020·全国八年级课时练习)已知31cm 的氢气的质量用科学记数法表示约为5910g -⨯,一块橡皮的质量为45g .(1)用小数表示31cm 的氢气质量;(2)这块橡皮的质量是31cm 的氢气质量的多少倍?【答案】(1)5910g 0.00009g -⨯=;(2)5510⨯倍【分析】(1)绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10−n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定;(2)利用有理数除法运算法则求出答案即可.【详解】(1)5910g 0.00009g -⨯=.(2)5450.00009500000510÷==⨯.故这块橡皮的质量是31cm 的氢气质量的5510⨯倍.【点睛】本题考查用科学记数法表示较小的数以及有理数除法等知识,一般形式为a ×10−n ,其中1≤|a |<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.20.(2021·西安市浐灞欧亚中学七年级期末)(1)计算:()()32224422a a a a a --⋅+-÷; (2)先化简,再求值:()()2222132522x y xyx y xy --+,其中1,2x y =-=. 【答案】(1)62a ;(2)22742x y xy -,23 【分析】(1)根据同底数幂的乘除法、幂的乘方及积的乘方、单项式除以单项式可直接进行求解;(2)先去括号,然后进行整式的加减运算,最后代值求解即可.【详解】解:(1)原式=86666622424a a a a a a a --+÷=-+=;(2)原式=2222225637422x x y y x x x y xy y y ---=-; 把1,2x y =-=代入得:原式=()()22712412716232⨯-⨯-⨯-⨯=+=. 【点睛】本题主要考查同底数幂的乘除法、幂的乘方、积的乘方、单项式除以单项式及整式的化简求值,熟练掌握同底数幂的乘除法、幂的乘方、积的乘方、单项式除以单项式及整式的化简求值是解题的关键. 21.(2020·江西南昌市·八年级期中)规定22a b a b *=⨯,求:(1)求13*(2)若2(21)32x *-=,求x 的值.【答案】(1)16;(2)2x =【分析】(1)直接利用已知22a b a b *=⨯,将原式按定义式变形得出答案;(2)直接利用已知将原式变形得出等式,再利用同底数幂相等指数相等列方程求出答案即可.【详解】解:(1)13*=1322⨯=16;(2)∵()22132x *-=,∵2215222x -⨯=∵21522x +=∵215x +=∵2x =.【点睛】本题主要考查了新定义运算以及同底数幂的乘法运算,正确的将原式按照定义式变形是解题的关键.利用同底数幂的乘法法则时应注意:底数必须相同;指数是1时,不要误以为没有指数.22.(2020·江苏泰州市·七年级期中)我们约定1010a b a b ⊕=⨯,如: 23523101010⊕=⨯=.(1)试求123⊕和48⊕的值;(2)想一想,()a b c ⊕⊕是否与()a b c ⊕⊕相等,并说明理由.【答案】(1)1512310⊕=;124810⊕=;(2)()a b c ⊕⊕=()a b c ⊕⊕;理由见解析.【解析】【分析】(1)根据1010a b a b ⊕=⨯,,可得答案;(2)根据1010a b a b ⊕=⨯,,可得同底数幂的乘法,根据同底数幂的乘法,可得答案.【详解】(1)根据题中的新定义得:123⊕=1012⨯103=1015;481248101010⊕=⨯=(2)相等,理由如下:∵()10101010a b c a b c a b c ++⊕⊕=⨯⨯=()∵()10101010a b c a b ca b c ++⊕⊕=⨯⨯=() ∵()a b c ⊕⊕=()a b c ⊕⊕【点睛】此题考查了同底数幂的乘法.此题比较简单,注意同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.23.(2019·莆田第十五中学七年级月考)我们已经学习过“乘方”运算,下面给同学们介绍一种新的运算,即对数运算.定义:如果b a =N (a >0,a ≠1,N >0),则b 叫做以a 为底N 的对数,记作log N a =b ,例如:因为35=125,所以1255log =3;因为211=121,所以12111log =2 (1)填空:66log = ,16log = ;(2)如果(2)2log m -=3,求m 的值.【答案】(1)1,0;(2)m =10.【分析】(1)把对数运算转化为幂运算求解即可;(2)把对数运算转化为幂的运算求解即可.【详解】解:(1)∵1066,61==,∵66log =1,16log =0,故答案为:1,0;(2)∵(2)2log m -=3,∵32=m ﹣2,解得:m =10.【点睛】本题考查了新运算问题,解答时,熟练将对数运算转化为对应的幂的运算是解题的关键.24.(2021·沭阳县修远中学七年级月考)(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )(2)请用字母表示第n 个等式,并验证你的发现.(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.【答案】(1)0,1,2;(2)证明见解析;(3)201821-【详解】试题分析:(1)根据0次幂的意义和乘方的意义进行计算即可;(2)观察各等式得到2的相邻两个非负整数幂的差等于其中较小的2的非负整数幂,即2n -2n -1=2n -1(n 为正整数);(3)由于21-20=20,22-21=21,23-22=22,…22018-22017=22017,然后把等式左边与左边相加,右边与右边相加即可求解.试题解析:(1)21-20=1=20;22-21=2=21;23-22=4=22,故答案为0,1,2;(2)观察可得:2n -2n -1=2n -1(n 为正整数),证明如下:2n -2n -1=2×2n -1-2n -1=2n -1×(2-1)=2n -1;(3)∵21-20=20,22-21=21,23-22=22,…22018-22017=22017,∵22018-20=20+21+22+23+…+22016+22017,∵20+21+22+23+…+22016+22017的值为22018-1.25.(2020·兴化市陈堡初级中学七年级月考)我们知道,根据乘方的意义:2a a a =⋅,3a a a a =⋅⋅. (1)计算:23a a ⋅=________,34a a ⋅=________;(2)通过以上计算你能否发现规律,得到n m a a ⋅的结果;(3)计算:23410a a a a a ⋅⋅⋅⋅⋅⋅⋅⋅.【答案】(1)5a ,7a ;(2)m nm n a a a +⋅=;(3)55a【分析】(1)根据有理数乘方的意义解答;(2)根据(1)的计算结果可得出运算规律:同底数幂相乘,底数a 不变,把指数把m 、n 相加即可; (3)根据(2)的规律进行计算即可得解.【详解】解:(1)235a a a a a a a a ⋅=⋅⋅⋅⋅=, 347a a a a a a a a a a ⋅=⋅⋅⋅⋅⋅⋅=,故答案是:5a ,7a ;(2)n m a a ⋅可以看做m n +个a 相乘,∵m n m n a a a +⋅=;(3)2341012341055a a a a a a a ++++⋅⋅⋅+⋅⋅⋅⋅⋅⋅⋅⋅==.【点睛】本题考查了有理数的乘方以及数式规律问题,明确有理数乘方的意义,得出规律是解题的关键.26.(2020·浙江杭州市·七年级期末)阅读下列各式:222333444(),(),()a b a b a b a b a b a b ⋅=⋅=⋅=回答下列三个问题:①验证:100122⎛⎫⨯= ⎪⎝⎭_________,100100122⎛⎫⨯= ⎪⎝⎭___________;②通过上述验证,归纳得出:()n a b ⋅=_________;()n a b c ⋅⋅=________;③请应用上述性质计算:201920182017(0.125)24-⨯⨯【答案】①1,1;②n n a b ,n n n a b c ;③-132. 【分析】①把问题分别转化为1001和100100100122⨯处理即可; ②将猜到规律推广到n 次方和三个因数情形即可;③把2019(-0.125)和20182分别变形为20172(-0.125)(-0.125)⨯和20172⨯2就可逆用上述规律计算即可.【详解】 ①∵1001001212⎛⎫⨯= ⎪⎝⎭=1, ∵100122⎛⎫⨯= ⎪⎝⎭1; ∵100100122⎛⎫⨯= ⎪⎝⎭1001001001212⨯=, ∵100100122⎛⎫⨯= ⎪⎝⎭1,故依次填1,1; ②∵100122⎛⎫⨯= ⎪⎝⎭1,100100122⎛⎫⨯= ⎪⎝⎭1, ∵100122⎛⎫⨯= ⎪⎝⎭100100122⎛⎫⨯ ⎪⎝⎭, 由此可得:()n a b ⋅=n n a b ;()n a b c ⋅⋅=n n n a b c ;故依次填n n a b ,n n n a b c ;③ ∵2019(-0.125)=20172(-0.125)(-0.125)⨯,201822017=2⨯2,∵201920182017(0.125)24-⨯⨯=20172(-0.125)(-0.125)⨯20172⨯⨯2×20174=20172(-0.12524)(-0.125)2⨯⨯⨯⨯ =1-32. 【点睛】本题考查了规律的验证,猜想和应用,熟练逆用同底数幂的乘法公式和发现的规律是解题的关键. 27.(2021·全国七年级专题练习)阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J .Napier ,1550年-1617年),纳皮尔发明对数是在指数概念建立之前,直到18世纪瑞士数学家欧拉(Euler ,1707年-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若(0,1)xa N a a =≠>,则x 叫做以a 为底N 的对数,记作log a x N =.比如指数式4216=可以转化为24log 16=,对数式52log 25=可以转化为2525=.我们根据对数的定义可得到对数的一个性质:a log(?)log M N M =+log (0,a 1,0,N 0)a N a M ≠>>>.理由如下:设a log M m =,a log N n =,所以m M a =,n N a =,所以m n m n MN a a a +==,由对数的定义得a log ()m n M N +=+,又因为a log log a m n M N +=+,所以log ()log log a a a MN M N =+.解决以下问题:(1)将指数35125=转化为对数式: .(2)仿照上面的材料,试证明:log log -log (0,1,0,0)a a a M M N a a M N N=≠>>> (3)拓展运用:计算333log 2log 18-log 4+= .【答案】(1)53log 125=;(2)见解析;(3)2【分析】(1)根据题意可以把指数式53=125写成对数式;(2)先设log a M =x ,log a N =y ,根据对数的定义可表示为指数式为:M =a x ,N =a y ,计算M N 的结果,同理由所给材料的证明过程可得结论;(3)根据公式:log a (M •N )=log a M +log a N 和log log -log aa a M M N N=的逆用,将所求式子表示为:log 3(2×18÷4),计算可得结论.【详解】(1)∵一般地,若a x =N (a >0,a ≠1),那么x 叫做以a 为底N 的对数,记作:记作:x =log a N . ∵3=log 5125,故答案为:3=log 5125;(2)证明:设log a M x =,log a N y =∵x M a =,y N a =, ∵xx y y M a a N a-==, 由对数的定义得log a M x y N=- 又∵log log a a x y M N -=-, ∵log log log (0,1,0,0)a a a M M N a a M N N=->≠>> (3)333log 2log 18-log 4+= log 3(2×18÷4)= log 39=2.故答案为:2.【点睛】本题考查整式的混合运算、对数与指数之间的关系与相互转化的关系,解题的关键是明确新定义,明白指数与对数之间的关系与相互转化关系.。
人教版八年级上册数学第十四章 (14. 1~14.2)检测题

八年级上册数学第十四章(14. 1~14.2)测试卷知识点一:同底数幂的乘法1.下列各题中的两个幂是同底数幂的是()A.-x²与(-x)³B.(-x)²与x²C.-x²与x³D.(a-b)⁵与(b-a)⁵2.下列各式中,运算正确的是()A. a³+a⁴=a⁷B.b³·b⁴=b⁷C.c³·c⁴=c¹²D.d³·d⁴= 2d⁷3.若x a·a²= a⁵,则x的值为()A.1 B.2 C.3 D.44.下列四个算式:①a³·a³= 2a³;②x³+ x³ =x⁶;③y³·y·y²=y⁶;④z²+ z²+ z²= 3z²,其中正确的个数是()A.1个B.2个C.3个D.4个5. 10³×10⁴=_____.6.(m-n)²(m-n)(m-n)⁵=_____.7.(-x)⁶·x⁷·x⁸=_____.8.已知a=-2,求(-a)²(-a) ³a⁴的值.知识点二:幂的乘方9.下列运算正确的是()A.(-2²)³=2⁶B.(-x⁴)⁵=x20C.(-x²ᵐ⁺¹)²=x⁴ᵐ⁺² D.[(x+y)²]⁷=(x+y)⁹10.(-aⁿ)²·aⁿ⁺¹等于()A.a²ⁿ⁺³B.a³ⁿ⁺¹C.-a³ⁿ⁺¹ D.-aⁿ⁺³11.下列各式中不正确的是()A.(m⁵)⁵=m²⁵B.(a⁴)ᵐ= (a²ᵐ)² C.x²ⁿ=(-xⁿ)²D.y²ⁿ=(-y²)ⁿ12.下列四个算式:①(a⁴)⁴=a⁴⁺⁴= a⁸;②[(b²)²]²- = b⁸;③[(-x)³]²=x⁶;④(-y)³=y⁶中,其中正确的算式有()A.0个B.1个C.2个D.3个13.填空题.(1)(5⁴)²=_____(2)=_____(3)(-a³)⁴=_____(4)(y²)³.y=_____(5)(a⁴)²+(a²)⁴=_____(6)(a²)².(a³)²=_____(7)c.(c⁵)².(-c)=_____(8)[(-m⁴)⁵.(-m²)⁷]²=_____(9)[(a-b)³]ᵐ.[(b-a)ᵐ]²=_____(10)(x²)ⁿ.(xⁿ¯¹)³=_____(11)当n为偶数时,[(-a²)ⁿ+(-aⁿ)²]²=_____(12)已知9⁵×27²=x3,则x=_____14.比较2100与3⁷⁵的大小.知识点三:积的乘方15.(-2x²y³)⁴的结果为()A.-2x⁸y¹²B.-2x²y¹²C.16x⁶y⁷D.16x⁸y¹²16.如果(2aᵐbᵐ⁺ⁿ)³=8a⁹b¹⁵成立,则m,n的值为()A.m=3, n-2B.m=3, n=9C.m=6, n=2D.m=2, n=517.(2×10²)³写成科学记数法的形式为()A.6×10⁵B. 0.6×10⁷C.8×10⁵D.8×10⁶18.填空题.(1)(ab)³=_____(2)(-x²y)⁵=_____(3)=_____(4) (0.1xy³)³=_____(5)(aⁿbᵐ)²=_____(6)(xⁿ⁺¹yⁿ¯¹)²=_____(7)(-3ab²)ᵐ=_____(8) (2²b⁵)²=_____(9)[(-2xy)³]²=_____(10) =_____知识点四:整式的乘方19.下列四个算式中,正确的是()A.3m(5a+2b)=3ma+6mb B.-2xy(3x²y-2xy²)=4x²y³- 6x³y²C.(x-3y)(-6x)=6x²- 18xy D.x⁶y²÷x²y =x³y20.如果计算(2-nx-3x²+ mx³)(-4x²)的结果中不含x⁵项,那么m应等于()A.0 B.1 C.-1 D.4121.已知(x-1)(x²+mx+n) =x³-6x²+11x-6,求m,n的值.22.对于任意自然数n,代数式n(n+7)-(n-3)(n-2)的值能被6整除吗?知识要点五:平方差公式23.下列多项式中,可以用平方差公式计算的是()A.(2a - 3b)(- 2a+3b) B.(- 3a+4b)(- 4b - 3a)C.(a-b)(b-a) D.(a-b -c)(-a+b+c)24.下列计算结果正确的是()A.(x+2)(x-2)=x²-2 B.(x+2)(3x-2)=3x²-4C .(ab-c)(ab+c)=a ²b ²-c ²D .(-x-y) (x+y) =x ²-y ² 25.已知(a+b-3)²+la- b+5l=0,求a ²-b ²的值.26.有两个正方体,棱长分别为acm ,bcm ,如果a-b=3,a+b=11,求它们的表面积的差.知识要点六:完全平方公式27.下列式子中是完全平方式的是( )A.a ²+ ab+ b ²B.a ²+2a+2C.a ²-2b+b ²D.a ²-2a+1 28.若(x-y)²=x ²+xy+y ²+N 则N 为( ) A. xy B .-xy C .3xy D .-3xy 29.填空题.(1)(8-y)²= 64+_____+y ²,(- x+y)²=_______2xy+y ²; (2)若kx ²+ 8x+1是一个完全平方式,则k=_____;(3)若x ²+kx+91=(x-31)²,则k=_____;(4)(a-3)²-a ²=_____;(5) (xy-1)²- (xy+1)²=_____.30.若x ²-2x+y ²+6y+10 =0,求x ,y 的值.31.证明:不论x ,y 取何值,代数式x ²+ y ²+ 4x-6y+13的值都不小于0.参考答案1.C2.B3.C4.B5. 10⁷6.(m-n )⁸ 7.x ²¹8.(-a )².(-a )³.a ⁴=(-a )².(-a )³.(-a )⁴=(-a )⁹= [-(-2)]⁹=2⁹. 9.C 10.B 11.D 12.C 13.(1)5⁸ (2)15)71((3) a ¹² (4) y ⁷ (5) 2a ⁸ (6) a ¹ᵒ(7) -c ¹² (8) m ⁶⁸ (9) (a-b)⁵ᵐ (10) X ⁵ⁿ¯³ (11) 4a ⁴ ⁿ (12) 16 14. 2¹ᴼᴼ=4252⨯=( 2⁴)²⁵=16²⁵, 3⁷⁵=3253⨯= (3³)²⁵=27²⁵,∵27²⁵> 16²⁵, ∴2¹ᴼᴼ< 3⁷⁵. 15.D 16.A 17.D18. (1) a³b³ (2) -x ¹ᴼy ⁵ (3) 278p ⁶q ⁹ (4) 0.001x³y ⁹(5) a ²ⁿb ²ᵐ (6) x ²ⁿ⁺²y ²ⁿ¯² (7) (-3)ᵐa ᵐb ²ᵐ (8) 16b ¹ᴼ (9) 64x ⁶y ⁶ (10)169-m ⁴n ⁶p ²19.B 20.A 21. m= -5.n=6 22. n(n+7)-(n-3)(n-2) =12n-6=6(2n-1) ∵6(2n -1)是6的倍数,∴能被6整除. 23.B 24.C 25.- 1526.表面积之差6(a ²-b ²) =6(a+b)(a-b)=6×11×3=198 (cm ²). 27.D 28.D29. (1) (-16y),x ² (2)16 (3)32-(4)-6a+9 (5) -4xy30.x ²- 2-x+y ²+6y+10=0,即(x ²-2x +1)+(y ²+6y+9)=0,即(x-1)²+(y+3)²=0,解得x=1,y=-3.31.x ²+y ²+ 4x-6y+13=x ²+4x +4+y ²-6y+9=(x+2)²+(y-3)², ∵(x+2)²≥0,(y-3)²≥0,∴(x+2)²+(y-3)²≥0.∴无论x,y 取何值,x ²+y ²+ 4x-6y+ 13的值都不小于0.。
七年级数学学探诊(有答案)

第十五章整式测试1 同底数幂的乘法学习要求会用同底数幂的乘法性质进行计算.课堂学习检测一、填空题1.同底数的幂相乘,______不变,______相加.2.直接写出结果:(1)104×105=______;m3·m6=______;a8·a=______;(2)102×107×10=______;y3·y4·y=______;(3)(-b)3·(-b)=______;(-a)3·(-a)5·(-a)=______.3.若a3·a m=a8,则m=______;若33x+1=81,则x=______.二、选择题4.b3·b3的值是( ).(A)b9(B)2b3(C)b6(D)2b6 5.(-c)3·(-c)5的值是( ).(A)-c8(B)(-c)15(C)c15(D)c8三、判断题6.a3·a3=2a3.( ) 7.y3+y3=y6.( )8.m4·m3=m12.( ) 9.(-c)3·(-c)4=-c7.( )四、计算题10.23×23×2.11.x n·x n+1·x n-1.12.(-m)·(-m)2·(-m)3.13.(a-b)·(a-b)3·(a-b)2.14.a2·a3+a·a4+a5.15.a·a4-3a2·a·a2.综合、运用、诊断一、填空题16.直接写出结果:(1)m·m n·m2=______;(2)b m+2·b2·b=______;(3)-x3·x·x7=______;(4)(-x3)·(-x)4=______;(5)-m2·(-m)3=______;(6)-(-c)3·(-c)=______;(7)23·2(______)=256;(8)(-a)2·(______)=-a5.17.若2m=6,2n=5,则2m+n=______.二、计算题18.1000×10a+2×10a-1.19.x4·(-x)3+(-x)6·(-x).20.25×54-125×53.21.(-2)2009+(-2)2010.拓展、探究、思考22.回答下列问题:(1)(-a)n与-a n相等吗?(2)(a-b)n与(b-a)n相等吗?(3)根据以上结论计算①(m-2n)4·(2n-m)2;②(m-n)4·(n-m)3.测试2 幂的乘方学习要求会用幂的乘方性质进行计算.课堂学习检测一、填空题1.幂的乘方,______不变,指数______.2.直接写出结果:(1)(102)3=_______;(2)(a4)3=_______;(3)(3n)3=_______;(4)[(-2)2]3=______;(5)[(-n)3]3=______;(6)(-32)5=______.3.用“=”或“≠”把下列两个式子连接起来:(1)m3·m3______m9;(2)(a4)4______a4·a4;(3)(a2)5______(a5)2;(4)a2·a2______(a2)2;(5)(-a2)3______(-a3)2;(6)[(-b)2]3______[(-b)3]2.二、选择题4.下列计算正确的是( ).(A)(x2)3=x5 (B)(x3)5=x15(C)x4·x5=x20(D)-(-x3)2=x65.(-a5)2+(-a2)5的结果是( ).(A)0 (B)-2a7(C)2a10(D)-2a10三、计算题6.(x2)3·x4.7.2(x n-1)2·x n.8.(x3)4-3(x6)2.9.m·(-m3)2·(-m2)3.10.[(-2)3]4·(-2)2.11.[(x-y)2·(x-y)n-1]2.12.[(a-b)3]2-[(b-a)2]3.综合、运用、诊断一、填空题13.直接写出结果:(1)3(x2)4=_______;(2)[(a+b)3]4=_______;(3)(x2m)4n=_______;(4)x4·(x2)5=_______;(5)(c2)m+1·c m+4=_______.14.化简(-x-y)2m(-x-y)3=_______.(m为正整数)15.若(a3)x·a=a19,则x=_______.16.已知a3n=5,那么a6n=______.二、选择题17.下列算式计算正确的是( ).(A)(a3)3=a3+3=a6(B)(-x2)n=x2n(C)(-y2)3=(-y)6=y6(D)[(c3)3]3=c3×3×3=c27三、计算题18.9(a3)2·(-a)2·(-b2)2+(-2)4·(a2)4·b4.四、解答题19.(1)若16x=216,求x的值;(2)若(9a)2=38,求a的值.拓展、探究、思考20.(1)若10α=2,10β=3,求102α+3β 的值;(2)若2x+5y-3=0,求4x·32y的值.21.比较大小:3555,4444,5333.测试3 积的乘方学习要求会用积的乘方性质进行计算.课堂学习检测一、填空题1.积的乘方,等于把积的每个因式______,再把所得的幂______. 2.直接写出答案:(1)(3×10)2=_______; (2)(mn )6=_______;(3)(b 4c )9=_______; (4)(-2x )2=_______; (5)32)51(b a -=_______;(6)[(-2xy 3)2]2=_______. 二、选择题3.下列计算正确的是( ). (A)(xy )3=xy 3 (B)(-5xy 2)2=-5x 2y 4 (C)(-3x 2)2=-9x 4(D)(-2xy 2)3=-8x 3y 6 4.若(2a m b n )3=8a 9b 15成立,则( ). (A)m =6,n =12 (B)m =3,n =12 (C)m =3,n =5(D)m =6,n =55.下列计算中,错误的个数是( ).①(3x 3)2=6x 6 ②(-5a 5b 5)2=-25a 10b 10 ③3338)32(x x -=- ④(3x 2y 3)4=81x 6y 7 ⑤x 2·x 3=x 5 (A)2个 (B)3个(C)4个(D)5个三、计算题6..)4()21(2332a a ⋅ 7.-(-2xy 2)3(-y 3)5.8.(x 2y 3)3+(-2x 3y 2)2·y 5. 9.(-2a )6-(-2a 3)2-[(-2a )2]3.四、解答题 10.当41=a ,b =4时,求代数式32233)21()(ab b a -+-的值. 综合、运用、诊断一、填空题11.化简:(1)33331)31(b a ab +-=_______;(2)(3a 2)3+(a 2)2·a 2=_______.12.直接写出结果:(1)(______)n =3n a 2n b 3n ; (2)x 10y 11=(______)5·y ; (3)若2n =a ,3n =b ,则6n =______. 二、选择题13.下列等式正确的个数是( ).①(-2x 2y 3)3=-6x 6y 9 ②(-a 2m )3=a 6m ③(3a 6)3=3a 9④(5×105)×(7×107)=35×1035 ⑤(-0.5)100×2101=(-0.5×2)100×2 (A)1个 (B)2个 (C)3个 (D)4个 三、计算题14.[-(a 2b )3·a ]3. 15.(4x 2y )3·(0.125xy 3)2. 16.52009×(-0.2)2010. 17..)21(6)31(675-⨯⨯- 四、解答题 18.若4)31()9(832=⋅x,求x 3的值.拓展、探究、思考19.比较216×310与210×314的大小. 20.若3x +1·2x -3x ·2x +1=22·32,求x .测试4 整式的乘法(一)学习要求会进行单项式的乘法计算.课堂学习检测一、填空题1.单项式相乘,把它们的__________分别相乘,对于只在一个单项式里含有的字母,则__________. 2.直接写出结果:(1)3ab 2·2a 2b 2=_______; (2)xyz y x 165.5232=_______; (3)5y ·(-4xy 2)=_______; (4)(-3a 2b )·(-5a 4)=_______;(5))92()2()23(2322c b a b a -⋅⋅-=_______;(6)(-a 2)·(4a 4)2=_______. 3.用科学记数法表示:(3×105)×(5×102)=_______. 4.已知a =2010,b 是a 的倒数,则(a n b 2)·ab n -2=_______. 二、选择题5.下列算式中正确的是( ). (A)3a 3·2a 2=6a 6 (B)2x 3·4x 5=8x 8 (C)3x ·3x 4=9x 4(D)5y 7·5y 7=10y 146.21-m 2n ·(-mn 2x )的结果是( ). (A)x n m 2421 (B)3321n m(C)x n m 3321 (D)x n m 3321-7.若(8×106)×(5×102)×(2×10)=M ×10a ,则M 、a 的值为( ).(A)M =8,a =10 (B)M =8,a =8 (C)M =2,a =9(D)M =5,a =10三、计算题8.).21()103(2333c ab bc a ⋅ 9.(4x m +1z 3)·(-2x 2yz 2).10.).32()43(5433c ab b a ab -⋅-⋅11.[4(a -b )m -1]·[-3(a -b )2m ].综合、运用、诊断 一、填空题 12.直接写出结果:(1)(-4a n -1b )·(-3a )=_______; (2))43()32()3(22xy y x x -⋅-⋅-=______;(3)(-2a 4)3·(3ab 3)3=______; (4))1031()103(322⨯⨯⨯=______;(5)(-x 2y m )2·(xy )3=______;(6)(-a 3-a 3-a 3)2=______.13.已知x 3a =3,则x 6a +x 4a ·x 5a =______. 二、选择题14.如果单项式-3x 2a -b y 2与31x 3a+by 5a+8b是同类项,那么这两个单项式的积是( ).(A)-x 10y 4(B)-x 6y 4(C)-x 25y 4(D)-x 5y 215.下列各题中,计算正确的是( ).(A)(-m 3)2(-n 2)3=m 6n 6 (B)(-m 2n )3(-mn 2)3=-m 9n 9 (C)(-m 2n )2(-mn 2)3=-m 9n 8 (D)[(-m 3)2(-n 2)3]3=-m 18n 18三、计算题16.-(-2x 3y 2)2·(-23x 2y 3)2. 17.(-2x m y n )·(-x 2y n )2·(-3xy 2)3. 18.(2a 3b 2)2+(-3ab 3)·(5a 5b ). 19.(-5x 3)·(-2x 2)·41x 4-2x 4·(-41x 5).0.-43(-2x 2y )2·(-31xy )-(-xy )3·(-x 2).21.-2[(-x )2y ]2(-3x m y n ).拓展、探究、思考22.若x =2m +1,y =3+4m ;(1)请用含x 的代数式表示y ; (2)如果x =4,求此时y 的值.测试5 整式的乘法(二)学习要求会进行单项式与多项式的乘法计算.课堂学习检测一、填空题1.单项式与多项式相乘,就是用单项式去乘_______,再把所得的积_______. 2.直接写出结果:(1)5(m +n -5)=_______; (2)-2a (a -b 2+c 3)=_______; (3)(-2a +3b )·(-4ab )=_______;(4))21()864(2x x x-⋅-+-=_______. 二、选择题3.整式a m (a m -a 2+7)的结果是( ).(A)a 2m -a 2m +7a m(B)2m a -a 2m +7a m (C)a 2m -a 2+m +7a m(D)2m a-a m +2+7a m4.化简a (b -c )-b (c -a )+c (a -b )的结果是( ). (A)2ab +2bc +2ac (B)2ab -2bc (C)2ab(D)-2bc5.方程2x (x -1)-x (2x -5)=12的解为( ). (A)x =2 (B)x =1 (C)x =-3 (D)x =4 三、计算题6.2a 2-a (2a -5b )-b (5a -b ). 7.2(a 2b 2-ab +1)+3ab (1-ab ).8.(-2a 2b )2(ab 2-a 2b +a 2). 9.-(-x )2·(-2x 2y )3+2x 2(x 6y 3-1).四、解答题10.已知m =-1,n =2时,代数式)43253(4)12(562---+-+--n m m n m m m的值是多少?11.若n 为自然数,试说明整式n (2n +1)-2n (n -1)的值一定是3的倍数.综合、运用、诊断-、填空题12.直接写出结果:(1)-ab (-a 2b 2+ab -1)=_________;(2))6()63121(2ab ab b a ab -⋅--=_________; (3)(2ab 2-3a 2b )·(3ab )2=_________; (4)(-2y )3(4x 2y -2xy 2)=_________. 二、选择题13.要使x (x +a )+3x -2b =x 2+5x +4成立,则a ,b 的值分别是( ).(A)a =-2,b =-2 (B)a =2,b =2 (C)a =2,b =-2 (D)a =-2,b =214.如果x 2与-2y 2的和为m ,1+y 2与-2x 2的差为n ,那么2m -4n 化简后为( )(A)-6x 2-8y 2-4 (B)10x 2-8y 2-4 (C)-6x 2-8y 2+4 (D)10x 2-8y 2+4 15.如图,用代数式表示阴影部分面积为( ).(A)ab (B)ac +bc(C)ac +(b -c )c (D)(a -c )(b -c )三、计算题16.4a -3[a -3(4-2a )+8].17.).3()]21(2)3([322b a b b a b ab -⋅--- 18.)].21(36[32y x xy xy xy --19..6)6121(2)2143(2121xy y x xy y x n n ⋅--⋅-++四、解答题20.解方程2x (x -2)-6x (x -1)=4x (1-x )+16.21.解不等式2x 2(x -2)+4(x 2-x )≥x (2x 2+5)-3.22.已知ax (5x -3x 2y +by )=10x 2-6x 3y +2xy ,求a ,b 的值.拓展、探究、思考23.通过对代数式进行适当变化求出代数式的值(1)若x +5y =6,求x 2+5xy +30y ;(2)若m 2+m -1=0,求m 3+2m 2+2009;(3)若2x +y =0,求4x 3+2xy (x +y )+y 3.测试6 整式的乘法(三)学习要求会进行多项式的乘法计算.课堂学习检测一、填空题1.多项式与多项式相乘,先用_______乘以_______,再把所得的积______. 2.直接写出结果:(1)(a +b )(m +n )=_______;(2)(a +2b )(x +y )=_______; (3)(m +n )(3y -a )=_______;(4)(y -3)(y +4)=_______. 二、选择题3.下面计算正确的是( ). (A)(2a +b )(2a -b )=2a 2-b 2 (B)(-a -b )(a +b )=a 2-b 2 (C)(a -3b )(3a -b )=3a 2-10ab +3b 2 (D)(a -b )(a 2-ab +b 2)=a 3-b 3 4.已知(2x +1)(x -3)=2x 2-mx -3,那么m 的值为( ). (A)-2 (B)2 (C)-5 (D)5 三、计算题 5.(2x +3y )(x -y ).6.).214)(221(-+x x7.(a +3b 2)(a 2-3b ). 8.(5x 3-4y 2)(5x 3+4y 2).9.(x 2+xy +y 2)(x -y ). 10.(x -1)(x +1)(2x +1).四、解答题11.若a =-2,则代数式(3a +1)(2a -3)-(4a -5)(a -4)的值是多少?12.已知(x -1)(2-kx )的结果中不含有x 的一次项,求k 的值.综合、运用、诊断一、选择题13.设M =(x -3)(x -7),N =(x -2)(x -8),则M 与N 的关系为( ).(A)M <N (B)M >N (C)M =N (D)不能确定 14.方程(x +4)(x -5)=x 2-20的解为( ).(A)x =0 (B)x =-4 (C)x =5 (D)x =40 二、计算题15.).12)(5(21+--a a16.-3(2x +3y )(7y -x ).17.)33)(2(3+-bb a .18.(3a +2)(a -4)-3(a -2)(a -1).三、解答题19.先化简,再求值:4x (y -x )+(2x +y )(2x -y ),其中x =21,y =-2.20.解不等式(x -3)(x +4)+22>(x +1)(x +2).21.在(x 2+ax +b )(2x 2-3x -1)的积中,x 3项的系数是-5,x 2项的系数是-6,求a 、b .22.已知(x 2+px +8)(x 2-3x +q )的展开式中不含x 2和x 3项,求p 、q 的值.拓展、探究、思考23.回答下列问题:(1)计算:①(x +2)(x +3)=________;②(x +3)(x +7)=______;③(a +7)(a -10)=_______;④(x -5)(x -6)=______.(2)由(1)的结果,直接写出下列计算的结果:①(x +1)(x +3)=______; ②(x -2)(x -3)=______;③(x +2)(x -5)=______; ④)31)(21(+-m m =______. (3)总结公式:(x +a )(x +b )=____________.(4)已知a ,b ,m 均为整数,且(x +a )(x +b )=x 2+mx +36,求m 的所有可能值.24.计算:(x -1)(x +1)=_________;(x -1)(x 2+x +1)=__________; (x -1)(x 3+x 2+x +1)=__________; (x -1)(x 4+x 3+x 2+x +1)=__________; ……猜想:(x -1)(x n +x n -1+x n -2+…+x 2+x +1)=_________.测试7 平方差公式学习要求会运用平方差公式进行计算.课堂学习检测一、填空题1.直接写出结果:(1)(x +2)(x -2)=_______; (2)(2x +5y )(2x -5y )=______; (3)(x -ab )(x +ab )=_______; (4)(12+b 2)(b 2-12)=______. 2.先观察、再计算:(1)(x +y )(x -y )=______; (2)(y +x )(x -y )=______; (3)(y -x )(y +x )=______; (4)(x +y )(-y +x )=______; (5)(x -y )(-x -y )=______; (6)(-x -y )(-x +y )=______. 二、选择题3.下列各多项式相乘,可以用平方差公式的有( ). ①(-2ab +5x )(5x +2ab ) ②(ax -y )(-ax -y ) ③(-ab -c )(ab -c ) ④(m +n )(-m -n ) (A)4个 (B)3个 (C)2个 (D)1个 4.若x +y =6,x -y =5,则x 2-y 2等于( ). (A)11 (B)15 (C)30 (D)60 5.下列计算正确的是( ). (A)(5-m )(5+m )=m 2-25 (B)(1-3m )(1+3m )=1-3m 2 (C)(-4-3n )(-4+3n )=-9n 2+16 (D)(2ab -n )(2ab +n )=4ab 2-n 2 三、计算题 6.).23)(23(22ba b a -+ 7.(x n -2)(x n +2).8.).3243)(4332(m n n m +-+ 9.⋅+-323.232xy y x10.).24)(24(y x y x --- 11.(-m 2n +2)(-m 2n -2).四、解答题12.应用公式计算:(1)103×97;(2)1.02×0.98;(3)⋅⨯769711013.当x =1,y =2时,求(2x -y )(2x +y )-(x +2y )(2y -x )的值.综合、运用、诊断一、填空题 14.)23)(23(aa ++-=_______. 15.(-3x -5y )(-3x +5y )=______.16.在括号中填上适当的整式:(1)(x +5)(______)=x 2-25; (2)(m -n )(______)=n 2-m 2; (3)(-1-3x )(______)=1-9x 2; (4)(a +2b )(______)=4b 2-a 2. 二、选择题17.下列各式中能使用平方差公式的是( ).(A)(x 2-y 2)(y 2+x 2)(B))5121)(5121(3232n m n m +--(C)(-2x -3y )(2x +3y ) (D)(4x -3y )(-3y +4x ) 18.下面计算(-7+a +b )(-7-a -b )正确的是( ).(A)原式=(-7+a +b )[-7-(a +b )]=-72-(a +b )2 (B)原式=(-7+a +b )[-7-(a +b )]=72+(a +b )2 (C)原式=[-(7-a -b )][-(7+a +b )]=72-(a +b )2 (D)原式=[-(7+a )+b ][-(7+a )-b ]=(7+a )2-b 2 19.(a +3)(a 2+9)(a -3)的计算结果是( ).(A)a 4+81 (B)-a 4-81 (C)a 4-81 (D)81-a 4 三、计算题20.).321)(213(2222a b b a +---21.(x +1)(x 2+1)(x -1)(x 4+1).22.(m -2n )(2n +m )-(-3m -4n )(4n -3m ).拓展、探究、思考23.巧算:(1);21)211)(211)(211)(211(15842+++++(2)(3+1)(32+1)(34+1)(38+1)…(n23+1).24.已知:x ,y 为正整数,且4x 2-9y 2=31,你能求出x ,y 的值吗?试一试.测试8 完全平方公式学习要求会运用完全平方公式进行计算,巩固乘法公式的使用.课堂学习检测一、填空题1.直接写出结果:(1)(x +5)2=_______;(2)(3m +2n )2=_______; (3)(x -3y )2=_______;(4)2)32(b a -=_______; (5)(-x +y )2=______;(6)(-x -y )2=______. 2.若9x 2+4y 2=(3x +2y )2+M ,则M =______. 二、选择题3.下列多项式不是完全平方式的是( ). (A)x 2-4x -4(B)m m ++241(C)9a 2+6ab +b 2(D)4t 2+12t +94.下列等式能够成立的是( ). (A)(a -b )2=(-a -b )2 (B)(x -y )2=x 2-y 2(C)(m -n )2=(n -m )2(D)(x -y )(x +y )=(-x -y )(x -y ) 5.下列等式不能恒成立的是( ). (A)(3x -y )2=9x 2-6xy +y 2 (B)(a +b -c )2=(c -a -b )2 (C)22241)21(n mn m n m +-=- (D)(x -y )(x +y )(x 2-y 2)=x 4-y 4三、计算题 6..)3243(2y x + 7.(3mn -5ab )2.8.(5a 2-b 4)2. 9.(-3x 2+5y )2.10.(-4x 3-7y 2)2. 11.(y -3)2-2(y +2)(y -2).四、解答题12.用适当方法计算:(1)2)2140(; (2)2992.13.若a +b =17,ab =60,求(a -b )2和a 2+b 2的值.综合、运用、诊断一、填空题14.(1)x 2-10x +______=( -5)2:(2)x 2+______+16=(______-4)2; (3)x 2-x +______=(x -______)2; (4)4x 2+______+9=(______+3)2.15.多项式x 2-8x +k 是一个完全平方式,则k =______. 16.若x 2+2ax +16是一个完全平方式,则a =______. 二、选择题17.下列式子不能成立的有( )个.①(x -y )2=(y -x )2 ②(a -2b )2=a 2-4b 2 ③(a -b )3=(b -a )(a -b )2 ④(x +y )(x -y )=(-x -y )(-x +y ) ⑤1-(1+x )2=-x 2-2x (A)1 (B)2 (C)3 (D)4 18.计算2)22(b a -的结果与下面计算结果一样的是( ). (A)2)(21b a - (B)ab b a -+2)(21(C)ab b a +-2)(41 (D)ab b a -+2)(41三、计算题19.(2a +1)2(2a -1)2. 20.(x -2y )2+2(x +2y )(x -2y )+(x +2y )2.21.(a +b +2c )(a +b -2c ). 22.(x +2y -z )(x -2y +z ).23.(a +b +c )2. 24..)312(2+-y x四、解答题25.一长方形场地内要修建一个正方形花坛,预计花坛边长比场地的长少8米、宽少6米,且场地面积比花坛面积大104平方米,求长方形的长和宽.26.回答下列问题:(1)填空:-+=+222)1(1x x x x ______=+-2)1(x x ______.(2)若51=+a a ,则221aa +的值是多少?(3)若a 2-3a +1=0,则221aa +的值是多少?拓展、探究、思考27.若x 2-2x +10+y 2+6y =0,求(2x -y )2的值.28.若a 4+b 4+a 2b 2=5,ab =2,求a 2+b 2的值.29.若△ABC 三边a ,b ,c 满足a 2+b 2+c 2=ab +bc +ca ,试问△ABC 的三边有何关系?测试9 同底数幂的除法学习要求会用同底数幂的除法性质进行计算.课堂学习检测一、填空题1.同底数幂相除,底数______,指数______.2.任何不等于0的数的0次幂都等于______,即a 0=______(a ≠0). 3.直接写出结果: (1)x 5÷x 2=______; (2)y 9÷y 8=______; (3)a 12÷a 12=_______; (4)(-c )4÷(-c )=_______;(5)(xy )8÷(xy )3=_______; (6)(-x )13÷x 12=_______; (7))2()21(4yy ÷=_______; (8)(-ax )5÷(ax )3=_______;(9)(a -b )3÷(a -b )=_______; (10)(π-3.14)0=_______.二、选择题4.下列计算不正确的是( ).(A)x 3m ÷x 3m -1=x (B)x 12÷x 6=x 2 (C)x 10÷(-x )2÷x 3=x 5 (D)x 3m ÷(x 3)m =1 5.如果将a 8写成下列各式,那么正确的有( ).①a 4+a 4 ②(a 2)4 ③a 16÷a 2 ④(a 4)2 ⑤(a 4)4 ⑥a 4·a 4 ⑦a 20÷a 12 ⑧2a 8-a 8 (A)7个 (B)6个 (C)5个 (D)4个 三、判断题(a ≠0) 6.a 6÷a 2=a 3.( ) 7.(-a )2÷a 2=-1.( ) 8.a 3÷1=a 2.( ) 9.54÷54=0.( ) 10.(-a )3÷(-a )2=-a .( ) 11.(a -3)0=1(a ≠3).( )四、计算题 12.(a 6)2÷a 5. 13.(x 2)3÷(x 3)2.14.(ab 2)4÷(ab 2)2. 15.[(a 2)3]4÷a 5.16.x 4m ÷x m ·x 2m . 17.(x 3·x 2·x 2)÷x 6.综合、运用、诊断一、填空题18.直接写出结果:(1)(-a 5)÷(-a )3=_______; (2)-a 4÷(-a )2=_______;(3)x 10÷x 4÷x 2=_______; (4)10n ÷10n -2=_______;(5)(a 3)m ÷a m =_______; (6)(y -x )2n ÷(x -y )n -1=_______. 19.若2(x -2)0有意义,则x ______________. 二、选择题20.下列计算中正确的是( ).(A)x a +2÷x a +1=x 2 (B)(xy )6÷(xy )3=x 2y 2(C)x 12÷(x 5÷x 2)=x 9 (D)(x 4n ÷x 2n )·x 3n =x 3n +221.若(y 2)m ·(x n +1)÷x ·y =xy 3,则m ,n 的值是( ).(A)m =n =1 (B)m =n =2 (C)m =1,n =2 (D)m =2,n =1 三、计算题22.[(x 3)2·(-x 4)3]÷(-x 6)3. 23.(x m ·x 2n )2÷(-x m +n ).24.(m -2n )4÷(2n -m )2. 25.(m -n )4÷(n -m )3.四、解答题26.(1)已知10m =3,10n =2,求102m -n 的值. (2)已知32m =6,9n =8,求36m -4n 的值.27.学校图书馆藏书约3.6×104册,学校现有师生约1.8×103人,每个教师或学生假期平均最多可以借阅多少册图书?拓展、探究、思考28.若2x =3,2y =6,2z =12,求x ,y ,z 之间的数量关系.29.若(a -1)a =1,求a 的值.30.已知999999=P ,909911=Q ,那么P ,Q 的大小关系怎样?为什么?测试10 整式的除法(一)学习要求会进行单项式除以单项式的计算.课堂学习检测一、判断题1.x 3n ÷x n =x 3.( ) 2.10x 4÷7x =0.7x 3.( ) 3..2121)(2x xy y x -=÷- ( ) 4.8a 8÷4a 4=2a 4.( ) 5.26÷42×162=512.( )6.(3ab 2)3÷3ab 3=9a 3b 3.( )二、选择题7.28a 4b 2÷7a 3b 的结果是( ). (A)4ab 2 (B)4a 4b(C)4a 2b 2 (D)4ab8.25a 3b 2÷5(ab )2的结果是( ). (A)a (B)5a (C)5a 2b (D)5a 2三、计算题9.-8x 4÷3x 2. 10.(-12a 5b 2c )÷(-3a 2b ).11..2383342ab b a ÷12..5.0)21(2242y x y x ÷-13.10a 3÷(-5a )2. 14.(4x 2y 3)2÷(-2xy 2)2.四、解答题15.先化简,再求值:[5a 4·a 2-(3a 6)2÷(a 2)3]÷(-2a 2)2,其中a =-5.综合、运用、诊断一、选择题 16.)21(43224yz x z y x -÷-的结果是( ). (A)8xyz (B)-8xyz (C)2xyz(D)8xy 2z 217.下列计算中错误的是( ).(A)4a 5b 3c 2÷(-2a 2bc )2=ab(B)(-24a 2b 3)÷(-3a 2b )·2a =16ab 2 (C)214)21(4222-=÷-⋅y x y y x (D)3658410221)()(a a a a a a=÷÷÷÷ 二、计算题18.(1.2×107)÷(5×104).19.(2a )3·b 4÷12a 3b 2.20.7m 2·(4m 3p 4)÷7m 5p . 21.(-2a 2)3[-(-a )4]2÷a 8.22.].)(21[)(122+++÷+n n y x y x23.⋅⨯⨯mmm m 42372三、解答题24.若22372288b b a b a nm=÷,求m ,n 的值.拓展、探究、思考25.已知x 2=x +1,求代数式x 5-5x +2的值.测试11 整式的除法(二)学习要求会进行多项式除以单项式的计算.课堂学习检测一、填空题1.直接写出结果:(1)(4x 2-8x +6)÷2=___________;(2)(28b 3-14b 2+21b )÷7b =___________; (3)(9a 3+6a 2-12a +3)÷(-3)=___________; (4)(6x 4y 3-8x 3y 2+9x 2y )÷(-2xy )=___________.2.已知A 是关于x 的四次多项式,且A ÷x =B ,那么B 是关于x 的_______次多项式. 二、选择题3.下列计算正确的是( ).(A)(-3x n +1y n z )÷(-3x n +1y n z )=0 (B)(15x 2y -10xy 2)÷(-5xy )=3x -2y (C)x xy xy y x 216)63(2=÷- (D)231123931)3(x x x x xn n n +=÷+-++ 4.已知7x 5y 3与一个多项式之积是28x 7y 3+98x 6y 5-21x 5y 5,则这个多项式是( ). (A)4x 2-3y 2 (B)4x 2y -3xy 2 (C)4x 2-3y 2+14xy 2 (D)4x 2-3y 2+7xy 3 三、计算题5..53)1095643(354336ax ax x a x a ÷-+-6.[2m (7n 3m 3)2+28m 7n 3-21m 5n 3]÷(-7m 5n 3).7.[(m +n -p )(m +p +n )-(m +n )2]÷(-p ).四、解答题8.先化简,再求值:[(3a +2b )(3a -2b )-(a +2b )(5a -2b )]÷4a ,其中a =2,b =-3.综合、运用、诊断一、填空题9.直接写出结果:(1)[(-a 2)3-a 2(-a 2)]÷(-a )2=____________;(2)(-81x n +5+15x n +1-3x n -1)÷(-3x n -1)=_____________; (3)(____________)·(-4x 2y 3)=8x 5y 4-2x 4y 5-12x 2y 7. 10.若M (a -b )3=(a 2-b 2)3,那么整式M =____________. 二、计算题11.[(m +n )(m -n )-(m -n )2+2n (m -n )]÷4n .12..9]31)3(2)3[(8723223242y x y y x x x y x ÷⋅-⋅-三、解答题 13.当21=a ,b =-1时,求(a 2b -2ab 2-b 3)÷b -(a +b )(a -b )的值.拓展、探究、思考14.已知多项式A =1343x -258,B =x 2+5x -1,C =2x 3-10x 2+51x -259,D =2x 5-x 3+6x 2-3x +1,你能用等号和运算符号把它们连接起来吗?参考答案第十五章 整式测试11.底数,指数. 2.(1)109;m 9;a 9.(2)1010;y 8.(3)b 4;-a 9.3.5;1. 4.C . 5.D . 6.×. 7.×. 8.×. 9.√. 10.128.11.x 3n . 12.m 6. 13.(a -b )6. 14.3a 5. 15.-2a 5.16.(1)m n +3. (2)b m +5.(3)-x 11.(4)-x 7.(5)m 5.(6)-c 4.(7)5.(8)-a 3.17.30. 18.102a +4. 19.-2x 7. 20.0. 21.22009.22.(1)(-a )n =⎪⎩⎪⎨⎧-)()(为正奇数为正偶数n n n a a . (2)⎪⎩⎪⎨⎧---=-)()()()()(为正奇数为正偶数n b a b a a b n n n (3)①(m -2n )6.②-(m -n )7.测试21.底数,相乘. 2.(1)106;(2)a 12;(3)33n ;(4)64;(5)-n 9;(6)-310.3.(1)≠;(2)≠;(3)=;(4)=;(5)≠;(6)=.4.B . 5.A . 6.x 10. 7.2x 3n -2. 8.-2x 12. 9.-m 13. 10.214.11.(x -y )2n +2. 12.0. 13.(1)3x 8;(2)(a +b )12;(3)x 8mn ;(4)x 14;(5)c 3m +6.14.-(x +y )2m +3 15.6. 16.25. 17.D .18.25a 8b 4. 19.(1)x =4;(2)a =2. 20.(1)108;(2)8. 21.5333<3555<4444.测试31.分别乘方;相乘.2.(1)9×102;(2)m 6n 6;(3)b 36c 9;(4)4x 2;(5)361251b a -;(6)16x 4y 12. 3.D . 4.C . 5.C . 6.2a 12.7.-8x 3y 21. 8.5x 6y 9. 9.-4a 6. 10.56.11.(1)33278b a ;(2)28a 6. 12.(1)3a 2b 3;(2)x 2y 2;(3)ab . 13.A . 14.-a 21b 9. 15.x 8y 9. 16.0.2. 17.-18. 18.±6. 19.216×310<210×314. 20.2.测试41.系数、相同字母的幂,连同它的指数作为积的一个因式.2.(1)6a 3b 4;(2)z y x 4381;(3)-20xy 3;(4)15a 6b ;(5)c b a 4532;(6)-16a 10. 3.1.5×108. 4.2010. 5.B . 6.C . 7.A . 8.544203c b a . 9.-8x m +3yz 5. 10.c b a 8525. 11.-12(a -b )3m -1. 12.(1)12a n b ;(2)3423y x -;(3)-216a 15b 9;(4)3×107;(5)x 7y 2m +3;(6)9a 6. 13.36. 14.A . 15.D . 16.-9x 10y 10.17.54x m +7y 3n +6. 18.-11a 6b 4. 19.3x 9. 20.0. 21.6x m +4y n +2.22.(1)y =(x -1)2+3;(2)12.测试51.多项式的每一项,相加.2.(1)5m +5n -25;(2)-2a 2+2ab 2-2ac 3;(3)8a 2b -12ab 2;(4)2x 3-3x 2+4x .3.C . 4.B . 5.D . 6.b 2.7.-a 2b 2+ab +2. 8.4a 5b 4-4a 6b 3+4a 6b 2. 9.10x 8y 3-2x 2. 10.27.11.3n 是3的倍数.12.(1)a 3b 3-a 2b 2+ab ;(2)33a 2b 2+2a 3b 2;(3)18a 3b 4-27a 4b 3;(4)-32x 2y 4+16xy 5.13.C . 14.A . 15.C .16.-17a +12. 17.-3a 3b 4. 18..2992322y x y x +19..232y x n +- 20.x =-8. 21.31≤x . 22.a =2;b =1. 23.(1)36;(2)2010;(3)0. 测试61.一个多项式的每一项,另一个多项式的每一项,相加.2.(1)am +an +bm +bn ;(2)ax +ay +2bx +2by ;(3)3my -ma +3ny -na ;(4)y 2+y -12.3.C . 4.D . 5.2x 2+xy -3y 2. 6..143122-+x x 7.a 3-3ab +3a 2b 2-9b 3. 8.25x 6-16y 4. 9.x 3-y 3. 10.2x 3+x 2-2x -1. 11.-43. 12.k =-2. 13.B . 14.A . 15.⋅---252112a a 16.-33xy +6x 2-63y 2. 17.ab 2+7ab -18a . 18.-a -14. 19.-8.20.x <4. 21.a =-1;b =-4. 22.p =3;q =1.23.(1)①x 2+5x +6;②x 2+10x +21;③a 2-3a -70;④x 2-11x +30.(2)①x 2+4x +3;②x 2-5x +6;③x 2-3x -10;④⋅--61612m m (3)x 2+(a +b )x +ab .(4)±37;±20;±15;±13;±12.24.x 2-1;x 3-1;x 4-1;x 5-1;x n +1-1.测试71.(1)x 2-4;(2)4x 2-25y 2;(3)x 2-a 2b 2;(4)b 4-144.2.(1)x 2-y 2;(2)x 2-y 2;(3)y 2-x 2;(4)x 2-y 2;(5)y 2-x 2;(6)x 2-y 2.3.B . 4.C . 5.C . 6.⋅-4924b a 7.x 2n -4. 8..1699422n m -9..233222y x -10.⋅-16422x y 11.m 4n 2-4. 12.(1)9991;(2)0.9996;(3)⋅494899 13.-15. 14..942-a 15.9x 2-25y 2. 16.(1)x -5.(2)-m -n .(3)3x -1.(4)2b -a .17.A . 18.C . 19.C . 20..94144a b - 21.x 8-1. 22.-8m 2+12n 2. 23.(1)2.(2)⋅-⨯+2132112n 24.x =8;y =5. 测试81.(1)x 2+10x +25;(2)9m 2+12mn +4n 2;(3)x 2-6xy +9y 2;(4)⋅+-934422b ab a (5)x 2-2xy +y 2;(6)x 2+2xy +y 2. 2.-12xy . 3.A . 4.C . 5.D .6.169x 2+xy +94y 2. 7.9m 2n 2-30mnab +25a 2b 2. 8.25a 4-10a 2b 4+b 8. 9.9x 4-30x 2y +25y 2. 10.16x 6+56x 3y 2+49y 4. 11.-y 2-6y +17. 12.(1)411640;(2)89401. 13.49;169. 14.(1)25;x ;(2)-8x ;x ;(3)21;41 (4)12x ;2x . 15.16. 16.±4. 17.B . 18.D . 19.16a 4-8a 2+1. 20.4x 2. 21.a 2+2ab +b 2-4c 2.22.x 2-4y 2-z 2+4yz . 23.a 2+b 2+c 2+2ab +2bc +2ac .24.⋅+-++-9134324422y x y xy x 25.长12米,宽10米. 26.(1)2;2;(2)23;(3)7. 27.25. 28.3. 29.相等.测试91.不变,相减. 2.1,1.3.(1)x 3;(2)y ;(3)1;(4)-c 3;(5)x 5y 5;(6)-x ;(7)83y ;(8)-a 2x 2;(9)a 2-2ab +b 2;(10)1. 4.B . 5.C . 6.×. 7.×. 8.×. 9.×. 10.√. 11.√.12.a 7. 13.1. 14.a 2b 4. 15.a 19. 16.x 5m . 17.x .18.(1)a 2;(2)-a 2;(3)x 4;(4)100;(5)a 2m ;(6)(x -y )n +1. 19.x ≠2.20.C . 21.D . 22.1. 23.-x m +3n . 24.m 2-4mn +4n 2. 25.-m +n .26.(1)29;(2)827. 27.20册. 28.2y =x +z . 29.a =0或a =2. 30.P =Q .测试10 1.×. 2.×. 3.×. 4.√. 5.×. 6.×. 7.D . 8.B . 9.238x -. 10.4a 3bc . 11..41ab 12.-y 2. 13.a 52. 14.4x 2y 2. 15.-25. 16.A . 17.D . 18.240. 19.232b . 20.4p 3. 21.-8a 6. 22.2(x +y )n +1. 23.1. 24.m =4;n =3. 25.5.测试11 1.(1)2x 2-4x +3;(2)4b 2-2b +3;(3)-3a 3-2a 2+4a -1;(4).2943223x y x y x -+- 2.三. 3.D . 4.C . 5..23245225x x a a -+- 6.-14m 2n 3-4m 2+3. 7.p . 8.8. 9.(1)-a 4+a 2;(2)27x 6-5x 2+1;(3).32124223y y x y x ++-10.(a+b)3.11.m-n.12.-1.13.1.14.B·C+A=D.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
知识改变命运
一、选择题:
1.下列运算正确的是 ( )
A. 326a a a ⋅=
B.5552b b b ⋅=
C. 844x x x =+
D. 56y y y ⋅=
2.计算222a a a a -⋅+⋅的结果为 ( )
A. 3a
B. 62a -
C. 33a
D. 6a -
3.如果36x a a a ⋅=,则x 等于 ( )
A. 2
B. 3
C. 4
D. 1
4.已知n 是大于1的自然数,则11)()(++-⋅-n n c c 可化简为 ( )
A. )1(2)(--n c
B. nc 2-
C. n c 2-
D. 22+n c
二、填空题:
5.(1)(-a )3⋅(-a )7= ; (2)x m+1x m-1= ;
(3)(-103)4×102= ; (4)2x x ⋅⋅ =x 8 ;
(5) ⋅x m-1=x m+2(m 是大于1的整数)
6. 若324+=x x ,则x= .
7.(x+y )2(x+y )5= .
8. 已知y x b a ==2,2(a 、b 为正整数),则b a +2= .
三、计算题:
9. 100100)2(2-⨯- 10.213a a -⋅
11.2433927⨯⨯⨯ 12.25(-)()x y y x ⋅-
知识改变命运
13.35(2)(2)(2)b b b -⋅-⋅- 14.32)(t t t ---
15.()()()m m n s t s t t s +-⋅-⋅- (m 、n 是正整数)
16.已知17322224=⨯⨯x x ,求x 的值.
17.已知,152,52,32===z y x 试说明x+y=z.
知识改变命运
沁园春·雪 <毛泽东>
北国风光,千里冰封,万里雪飘。
望长城内外,惟余莽莽; 大河上下,顿失滔滔。
山舞银蛇,原驰蜡象,
欲与天公试比高。
须晴日,看红装素裹,分外妖娆。
江山如此多娇,引无数英雄竞折腰。
惜秦皇汉武,略输文采;
唐宗宋祖,稍逊风骚。
一代天骄,成吉思汗,
只识弯弓射大雕。
俱往矣,数风流人物,还看今朝。
知识改变命运。
