实验三伯努利方程应用
伯努利方程实验实验报告

伯努利方程实验实验报告伯努利方程实验实验报告引言:伯努利方程是流体力学中重要的基本方程之一,描述了流体在不同位置的速度、静压力和动压力之间的关系。
本实验旨在通过实验验证伯努利方程,并探究其在不同条件下的适用性。
实验目的:1. 验证伯努利方程在理想条件下的适用性;2. 探究伯努利方程在流体流动中的应用。
实验器材:1. 曲线管;2. 水泵;3. 流量计;4. 压力计。
实验步骤:1. 将曲线管固定在实验台上,并调整其位置,使其水平放置;2. 将水泵接入曲线管的一端,并将另一端与流量计连接;3. 打开水泵,调整水泵的流量,记录流量计的读数;4. 使用压力计分别测量曲线管的两端压力,并记录下来;5. 重复步骤3和步骤4,改变水泵的流量和曲线管的位置,以获取更多的数据。
实验结果:通过实验测量得到的数据,我们可以计算出曲线管中流体的速度、静压力和动压力,并利用伯努利方程验证实验结果的准确性。
讨论:1. 在实验中,我们可以观察到当流体速度增大时,静压力下降,动压力增大,这符合伯努利方程的预期结果;2. 实验中我们还可以改变曲线管的形状和水泵的流量,观察伯努利方程在不同条件下的适用性;3. 由于实验过程中存在一些实际条件的限制,如流体黏性、管壁摩擦等,可能会对实验结果产生一定的影响。
结论:通过实验验证,我们得出结论:伯努利方程在理想条件下是成立的。
在流体流动中,速度增大时,静压力下降,动压力增大。
然而,在实际情况下,由于黏性和摩擦等因素的存在,伯努利方程可能会有一定的误差。
实验的局限性:1. 实验中忽略了流体的黏性和摩擦等因素,这可能会对实验结果产生一定的影响;2. 实验中使用的是理想曲线管,而实际情况中的管道通常并非完全光滑,这也可能会对实验结果产生一定的误差。
改进方向:为了提高实验的准确性,可以考虑以下改进方向:1. 在实验中引入流体黏性和摩擦等因素,以更贴近实际情况;2. 使用实际工业中常见的管道材料和形状,以更准确地模拟实际流动情况。
流体力学 伯努力方程
测流速原理该点在水面下的深度为d故该处的压强pgdb点在管口之前流速v根据伯努利方程所以在实际应用时上式须修正为其中c为比多管的修正系数由实验来确定
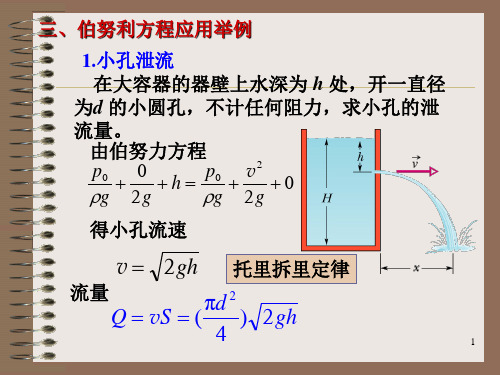
三、伯努利方程应用举例 1.小孔泄流 在大容器的器壁上水深为 h 处,开一直径 为d 的小圆孔,不计任何阻力,求小孔的泄 流量。 由伯努力方程 p0 p0 v 2 0 h 0 g 2 g g 2 g
h1
B
C A
pC p0 gh1
h2
其中p0为大气压
11
(2)当虹吸管下端开启时, h1 下端和A处的压强仍为:
p下 端 p0 , pA p0
B
C A
h2
而vB vc v下端 , v A 0 . 所以 pB p0 g( h2 h1 ) , pC p0 gh2
(2)取1-2-4的一个流线,由伯努利方程
P1 1 2 1 1 v1 P2 v 2 P4 v2 2 4 2 2 2 P4 P0
1 2 2 P1 P0 v 4 v1 P0 100, P1 -P0 100Pa 2 1 2 2 P2 P0 v 4 v 2 P0 , 2 P3 =P0 P2 P0 0 P3 P0 0
Qv v1S1 v2 S2
2( 汞 )g hS1 S 2
2 2
( S1 S 2 )
2 2
6
H
1 1 2 2 p1 v1 p2 v2 2 2
v1S1 v2 S2
v1 主管 细管 v2
p p1 p2 gh
•
Q v1S1 S1S2
例题2 在如图所示的虹吸管装置中,已 知 h1 和 h2 ,试问:(1)当截面均匀的虹吸管 下端被塞住时,A、B和C处的压强各为多大? (2)当虹吸管下端开启时,A、B和C处的压 强又各为多大? 这时水流出虹吸管的速率为 多大?
伯努利方程的应用例题

3
实ห้องสมุดไป่ตู้应用
伯努利方程能够用于许多实际领域,例如航空、航天、化学、水力学等。实际应 用的例子下面会详细介绍。
伯努利方程的应用
应用例题一
水流速度和压强的关系 在水力学领域中,经常需要测量流体的流速和压强。伯努利方程可以精确地计算流体流速和压强之间 的关系,帮助我们更好地了解流体力学特性。
应用例题二
管道中的流量计算 在工程领域中,经常需要估算管道内的水流量。利用伯努利方程,可以精确地计算不同位置、不同时 间段内的水流量,帮助我们更好地设计和调整管道系统。
感谢大家的收听
1
了解更多
如果你对伯努利方程的应用例题还有疑
交流互动
2
问或者想了解更多相关内容的话,可以 通过一些科学教育网站和专业书籍深入
如果大家对伯努利方程的实际应用有其
学习。
他的研究发现或者想法的话,可以通过
邮箱或者社交媒体等方式与我分享。
应用例题三
飞机表面压强的变化 在航空领域中,伯努利方程可以用于研究飞机表面压强的变化。这些压强变化既会影响到飞机的安全 性,也会影响到其性能和飞行效率。
总结和应用建议
科学实验
通过伯努利方程,我们可以更加 深入地了解流体力学的特性,例 如流体的压强、流速等。可以利 用流量计、压力计等科学实验装 置,进一步探究伯努利方程的实 际应用。
伯努利方程的应用例题
伯努利方程是描述流体在不同环境下运动和力量变化的重要公式。这个方程 的具体形式和实际应用都非常广泛,下面给大家展示几个实际应用的例子。
什么是伯努利方程?
1
原理
伯努利方程能够准确地描述流体内部的压强、动能和势能之间的关系。
2
基本形式
伯努利方程的应用

,伯努利方程及其应用伯努利,1738,瑞士。
动能与压强势能相互转换。
沿流线的伯努利方程将牛顿第二定律应用于控制体内的流体元,沿流线切线方向整理后因为将流体元的加速度转换成欧拉形式的加速度,沿流线的质点导数为则导出得:沿流线积分对于不可压定常流动,则可简化为(3皮托(简称皮托管,为纪念法国人皮托1.5 mm mm)在距前端适B点),在孔后足够长距离处两管弯090成柄状.测速时管轴线沿来流方向放置.设正前方的流速保持为v,静压强为p,流体密度为ρ。
粗细两管中的压强被引入U形测压计中,U形管中液体密度ρ。
试求用U形管液位差h∆m表示流速v的关系式。
解:设流动符合不可压缩无粘性流体定常流动条件。
从皮托管正前方A点到端点O再到侧壁孔B点的AOB线是一条流线,A点的速度和压强分别为v 和p ,沿流线AO段按(B4.3.4)式列伯努利方程A gz v+22+ρρ022p gz pv++=得0p 因v v B =k 解:= ⎝⎛22g 沿流线法向方向的速度压强关系式由牛顿第二定律:得考虑到几何关系,有 整理,得忽略重力,得若密度为常数,则有 RvnA A A n p p A p n A g 2( cos δρδρδδδθδδρ-==∂∂+-+此式为沿流线法向方向的伯努利方程,应用条件为(1)无粘性流体,(2)不可压流体(3)定常流(4)沿流线法向。
如果流线位直线时,曲率半径为无限大,则 此式与静压力公式相同。
沿总流的伯努利方程hg z z g h g m∆-=--∆=)1( )( m34ρρρ应用连续性方程伯努利方程的意义不可压缩粘性流体内流管道入口流动示意图,设管直径为d,管口外均流速度为U 。
从开始,流体在壁面上被滞止,形成边界层。
边界层外仍保持为均流,称为核心流。
由壁面不滑移条件引起壁面附近的流速降低,为满足质量守恒定律,核心流流速增大,速度廓线由平坦逐渐变为凸出。
随着边界层厚度不断增长,核心流不断加速,直至处四周的边界层相遇,核心流消失,整个管腔被边界层流动充满,此后速度廓线不再变化。
伯努利方程实验实验报告

伯努利方程实验实验报告实验名称:伯努利方程实验实验目的:1.验证伯努利方程的有效性;2.学习使用伯努利方程进行流体力学分析;3.掌握测量流体压力和流速的实验技巧。
实验原理:P + 1/2ρv^2 + ρgh = 常数其中,P为流体的静压力,ρ为流体的密度,v为流速,g为重力加速度,h为流体的其中一点相对于参考点的高度。
伯努利方程表明了流体流动过程中的能量守恒。
实验器材:1.伯努利装置(包括水槽、水泵、流量调节阀、压力计等材料)2.压力计3.流速计实验步骤:1.构建伯努利装置,包括水泵接通电源,调节流量阀使水槽中的水量保持稳定。
2.选取三个高度不同的位置,在各个位置上分别测量对应的静压力、流速和高度。
3.使用压力计分别测量各个位置的静压力,并记录下来。
4.使用流速计分别测量各个位置的流速,并记录下来。
5.使用尺子测量各个位置处相对于参考点的高度,并记录下来。
实验数据记录:位置1:静压力:P1=20Pa流速:v1=1m/s相对高度:h1=0m位置2:静压力:P2=30Pa流速:v2=1.5m/s相对高度:h2=1m位置3:静压力:P3=40Pa流速:v3=2m/s相对高度:h3=2m实验结果计算:根据伯努利方程,我们可以得到以下等式:P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2 = P3 +1/2ρv3^2 + ρgh3代入实验数据:20+1/2×ρ×1^2+ρ×0×9.8=30+1/2×ρ×1.5^2+ρ×1×9.8=40+1 /2×ρ×2^2+ρ×2×9.8化简等式,解方程组,求解出流体密度ρ。
实验讨论:通过实验测量的数据进行计算,我们可以得到流体密度的数值。
对于实验结果的误差分析和原因探究,可以从测量仪器的精度、实验操作的误差以及系统误差等方面进行分析。
实验三 伯努利方程应用

验 次
入 标
间
头Z(m)
压头hs(m) 压头hst(m) 压头hd(m) hw(m)
数
准 容
1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 hwo-1 hwo-2 hwo-3 hwo-4
量
筒
的
体
积
1
2
3
4
实 验 各点的流 次 动速度 数 Umax
实验整理数据表格(Ⅳ)
雷诺数 Remax
u 2ghd 。此流体流速为圆形管道截面中心的最大速度
umax 。
由 W umax 与 Re max关系。可查表得平均速度值W,最后计算 出流体得流量。
(四)实验项目
1、观察位置水头,压力水头,速度水头和能量损失得沿途变化 规律。
2、由皮托管测得流体流速,算出流量后和实际流量比较看是否 一致(计算出误差),以此来验证皮托管道的测速原理。
W2 2g
——局部阻力损失,
二局阻力损失。
2、测速管也称动压管或皮托一静压管,是将总压测孔和 静压测孔做在一根管子上的复合管。本实验中把皮托管插 在圆形管道截面的中心处,当测速管的小孔正对流体流动 孔方垂向直时于,流测体得流流动体方流向动时的,总测压得头流h体s 流Pr动总 ;的当静测压速头管hs的小Pr静 。流体流动的动压头hd hs hst 。流体流动点的速度
P1 , P2 ——压力势能所产生的流体柱的高度(m) rr
W12 , W22 ——动能所产生的流体柱的高度(m)
2g 2g
hw hL hm ——单位重量流体的沿程损失和局部能量损
失(m)
hL
L d
W2 2g
——沿程阻力损失,
大学物理伯努利方程及其应用

1 2 1 2 P v1 gh1 P2 v2 gh2 1 2 2 1 2 或 P v gh C 2
上式即为伯努利方程的数学表达式。
二、伯努利方程的意义
(1)伯努利方程的实质是功能原理在流体力学中的应用
表示单位体积流体流过细流管 S1 S 2 外压力所做的功; P 1 P 2
A1 F1v1t P 1S1v1t P 1V A2 F2v2 t P2 S2v2 t P2 V
由功能原理 :
Δt
S1
S2
P h2p 即
h1
1 2 2 (P P ) V ( v v 1 2 2 1 ) V g ( h2 h1 ) V 2
(3)注意统一单位,为国际单位。适用于理想流体的定常流动。 (4)P、h、v 均为可测量,他们是对同一流管而言的。
(5)它是流体力学中的基本关系式,反映各截面处,P、h、v 之间的关系。
三、伯努利方程的应用
小孔流速 如图所示,且SB<<SA,以 A、B 两点为参考点, 由伯努利方程:
SA
SB
SB S A v A S B v B 可知, v A v B 0 SA 选取hB处为参考点,其 hB=0, hA=h 得
得 v2 = 4v1 = 4 m•s-1
又由 得
1 2 1 2 p1 v1 p 2 v2 2 2 1 2 p1 p2 v2 v12 2 1 1.0 103 4 2 12 7.5 103 Pa 2
例 水从图示的水平管道1中流入,并通过支管2和3流入管4。 如管1中的流量为900cm3•s-1. 管1、2、3的截面积均为15cm2, 管4的截面积为10cm2,假设水在管内作稳恒流动, 求 (1)管2、3、4的流量; (2)管2、3、4的流速;
伯努利(Bernoulli)方程的应用

2020/7/24
19
3.6 伯努利(Bernoulli)方程的应用
三、伯努利方程应用时特别注意的几个问题
(3) 选好基准面,基准面原则上可以选在任何位置,但选择 得当,可使解题大大简化,通常选在管轴线的水平面或自由 液面,要注意的是,基准面必须选为水平面。
(4) 求解流量时,一般要结合一维流动的连续性方程求解。伯 努利方程的p1和p2应为同一度量单位,同为绝对压强或者同 为相对压强,p1和p2的问题与静力学中的处理完全相同。
qV实
Cd qV
Cd
4
d
2 2
2g(液 )h液 [1 ( A2 / A1 )2 ]
Cd为流量系数,通过实验测定。
2020/7/24
16
除文丘里流量计外,工程上常用的还有孔板流量 计和喷嘴流量计,它们都属于节流式流量计。
孔板流量计
2020/7/24
17
涡 轮 流 量 变 送 器 喷嘴流量计
(5) 有效截面上的参数,如速度、位置高度和压强应为同一 点的,绝对不许在式中取有效截面上A点的压强,又取同一 有效截面上另一点B的速度。
2020/7/24
20
【例3-7】 有一贮水装置如图3-22所示,贮水池足够大,当 阀门关闭时,压强计读数为2.8个大气压强。而当将阀门 全开,水从管中流出时,压强计读数是0.6个大气压强, 试求当水管直径d=12cm时,通过出口的体积流量(不计流 动损失)。
二、文特里(Venturi)流量计
以文特里管的水平轴线所在水平面作为基准面。
列截面1-1,2-2的伯努利方程
0 p1 V12 0 p2 V22
g 2g
g 2g
V2
2( p1 p2 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.001)
(五)实验步骤
1、熟悉实验设备,了解测速管的安装位置及使用方法, 记录水不流动时测压管读数及各点的位压头,测量水温及 大气压强。
2、启动水泵向稳压水箱充水,使稳压水箱始终保持溢流。
验 次
入 标
间
头Z(m)
压头hs(m) 压头hst(m) 压头hd(m) hw(m)
数
准 容
1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 hwo-1 hwo-2 hwo-3 hwo-4
量
筒
的
体
积
1
2
3
4
实 验 各点的流 次 动速度 数 Umax
实验整理数据表格(Ⅳ)
雷诺数 Remax
u 2ghd 。此流体流速为圆形管道截面中心的最大速度
umax 。
由 W umax 与 Re max关系。可查表得平均速度值W,最后计算 出流体得流量。
(四)实验项目
1、观察位置水头,压力水头,速度水头和能量损失得沿途变化 规律。
2、由皮托管测得流体流速,算出流量后和实际流量比较看是否 一致(计算出误差),以此来验证皮托管道的测速原理。
(一)实验目的
1、当流体在管内作定常流动时,观察位置水头Z、压力水
头 P 、速度小头W2/2g和能量损失的沿途变化规律,从 r
而加深对伯努利方程的理解。 2、通过实验了解并验证皮托管的测速原理。 3、验证沿程阻力损失和局部阻力损失的计算公式。
(二)实验设备
实验设备如图3—1所示,水用水泵压至稳压水箱。 稳压水箱内的水靠溢流俩维持稳定的液面,以保证管内的 流动是定常的。实验管道由管径不同的管子联接而成。管 道上开有4个测压孔,分别用测压管测量流体流动的总压 头和静压头,同时可以观察沿管各处的能量变化。
P1 , P2 ——压力势能所产生的流体柱的高度(m) rr
W12 , W22 ——动能所产生的流体柱的高度(m)
2g 2g
hw hL hm ——单位重量流体的沿程损失和局部能量损
失(m)
hL
L d
W2 2g
——沿程阻力损失,
f Re• 为沿程阻力系数
D
hm
W2 2g
——局部阻力损失,
3、打开阀门。分别让测压管的测头小孔正对和垂直流动 方向,记录各测压管的读数。
4、在阀门处,利用秒表和量筒量取实际流量。
5、重复以上实验2~3次。
(六)数据整理
实验记录表格: 水 温t= ; 大气压强P= ;运动粘度v= ; 管径d1= ;管 径d2= ; 管径d3= ;管 径d4= ; 实验记录表格及整理表格(见下页)来自0上水
水
管
0
箱
1测
压 管
2
3
标
尺
溢流管
水泵
水
箱
4
阀 门
回水管 角 铁 架
图3-1 伯努利方程应用实验简图
(三)实验原理
1、不可压缩的粘性流体沿管道做定常流动时,流体流动 遵循伯努利能量方程。
Z1
P1 r
W12 2g
Z2
P2 r
W22 2g
h
(m流动柱)
Z1、Z2——距基准面的位置高度(m)
各有效截 面平均速
度W
计算流量
计算能量损失
1 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 h`wo-1 h`wo-2 h`wo-3
h`wo-4
2
3
4
二局阻力损失。
2、测速管也称动压管或皮托一静压管,是将总压测孔和 静压测孔做在一根管子上的复合管。本实验中把皮托管插 在圆形管道截面的中心处,当测速管的小孔正对流体流动 孔方垂向直时于,流测体得流流动体方流向动时的,总测压得头流h体s 流Pr总动;的当静测压速头管hs的小Pr静 。流体流动的动压头hd hs hst 。流体流动点的速度
(七)思考题
1、为什么稳压水箱中要保持水始终溢流? 2、测压管测量的压强是绝对压强还是相对压强? 3、实验时发现管道中有气泡,你将怎么办?气泡是否对实 验有影响? 4、流体静止时,各测压管中的水面高度是否与稳压水箱高 度在同一平面上,为什么?
实验记录表格(Ⅲ)
实 流 时 各点位压 流动时总 流动时静 流动时动 稳定水箱至各点的能量损失
