正弦三角函数的图像与性质
正弦函数的性质与图像

x
sin x
1 s in x
0 0
π 2
π
0
3π 2
2 π
1 2
1
0
1
1
0
1
描点作图
y
2 1
-
y 1 sin x , x [ 0, 2 π ]
π 2
o
1-
π
3π 2
2π
x
y sin x , x [ 0, 2 π ]
用“五点法”画出下列函数在区间[0,2π]的图。 (1)y=2+sin x; (2)y=sin x-1; (3)y=3sin x.
y
1
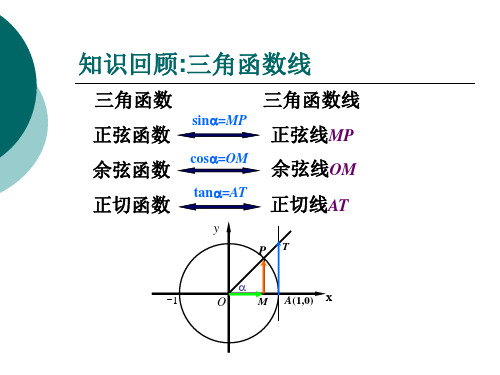
p (c o s x , s in x )
o
M
1
x
正弦线 MP
三角函数 问题
几何问题
正弦函数的图象
利用正弦线作出 y sin x , x 0, π 的图象. 2
y
作法: (1) 等分; (2) 作正弦线;
/
1P1
p1
(3) 平移; (4) 连线.
π 3
π 2
6
-
-
o1
M
-1 A
π 2
,1 );
与 x 轴的交点: ( 0 , 0 ), ( π , 0 ), ( 2 π , 0 ); 图象的最低点:
( 3π 2 , 1) .
五点 作图法
五 点 作 图 法
列表:列出对图象形状起关键作用的五点坐标.
描点:定出五个关键点.
连线:用光滑的曲线顺次连结五个点.
例 用“五点法”画出下列函数在区间[0,2π]的简图。 (1)y=-sin x; (2)y=1+sin x.
三角函数的图象与性质 (共44张PPT)

(
)
3 3 A.-2,2 3 3 3 3 C. - , 2 2
解析: 当 故
π π 1 π π 5π x∈0,2 时, 2x- ∈- 6, 6 , sin2x-6 ∈-2,1, 6
上是减函数 - π , 0 C.在[0,π]上是增函数,在
)
π π π π D.在2,π和-π,-2上是增函数,在-2,2 上是减函数
3.(2015· 皖南八校模拟)函数 f(x)=cos 2x+2sin x 的最大值与最小值 的和是 A.-2 3 C.- 2
4.求函数 y=cos x+sin
2
π x|x|≤4 的最大值与最小值.
π 2 2 解:令 t=sin x,∵|x|≤ ,∴t∈- , . 4 2 2
∴y=-t
2
1 2 5 +t+1=-t-2 + , 4
1- 2 1 5 2 ∴当 t= 时,ymax= ,当 t=- 时,ymin= . 2 4 2 2 ∴函数 y=cos x+sin
sin 2x>0, 解析:由 2 9-x ≥0,
π kπ<x<kπ+ ,k∈Z, 2 得 -3≤x≤3.
π π ∴-3≤x<- 或 0<x< . 2 2 ∴函数 y=lg(sin 2x)+ 9-x
2
π π 的定义域为-3,2 ∪0,2 .
2
π 1- 5 x通法]
1.三角函数定义域的求法 求三角函数定义域实际上是构造简单的三角不等式(组),常借 助三角函数线或三角函数图象来求解.
2.三角函数值域的不同求法 (1)利用 sin x 和 cos x 的值域直接求;
正弦和余弦的图像和性质
y sin x, x [0, 2 ]的图象 作法: (1) 等分
(2) 作正弦线
问题:如何作出比较精确的正弦函数图象? (3) 平移
途径:利用单位圆中正弦线来解决。
(4) 连线
y
B
1
用光滑曲线将这些正弦线 的终点连结起来!
A
O1
O 2 5 7 4 3 5 11 22
2
(
,1)
(
2 ,1)
(
2
,1)
(
2
,1)
( 2( ,21),1) ( 2 ,1)
,0) 3
(
2
( ,0) 2
(
((((((,,0,00),)0,),(003)2))(32,(-312,(1)32),1(33,)(212(3(323)2,21-,1,-),-1)-11)))
2 ,0) x
2 ,0)
解: x
3
0
2
2
2
sinx
0
1
0
-1
0
1+sinx
1
2
1
0
1
y
2
y=1+sinx,x[0, 2]
1
o
2
-1
2
3
2
x
2
典型例题:
例1(2) 画出函数y= -cosx,x[0, 2]的简图:
x
0
2
3
2
2
cosx
1
0
-1 0
1
-cosx
-1
0
1
0
-1
y
1
y=-cosx,x[0, 2]
正弦函数和余弦函数的图像与性质.ppt

, 0), (2 ,1)
2
2
并注意-4 曲线的“凹凸”变化.
课堂练习
1.作函数 y sin x 与 y sin x 1在 [0, 2 ]
上的大致图像. 2.指出1.中各图像与正弦函数图像的位置关系.
3.作函数 y cos x, x [ , ]的大致图像.
4.利用3.解不等式:cos x sin x, x [ , ]
-2
五个关键点:(0, 0), ( ,1), ( , 0), (3 , 1), (2 , 0)
2
2
利用五个关-4键点作简图的方法称为“五点法”
10
三、余弦函数的图像
根据诱导公式
cos
8
x
sin(
x) 可知余弦函数
y
cos
6
x的图像可由
y
2 sin
x
的图像向左平移
2
4
个单位得到.
1
2
2
-10
3-5
0
2
1
-2
余弦函数的值域是[1,1] -4
当且仅当 x 2k , k Z 时, -6
余弦函数取得最大值1;-8
5
2
35
x10
2
yP
OM x
当且仅当 x 2k , k-10 Z 时,
余弦函数取得最小值-1-1.2例1.求下列函数的源自大值与最小值,及取到最值6
课堂练习答案
12
1. y sin x, x [0, 2 ] y4
10
x
0
2
3 2
2
2 8
5
-10
正弦型函数的图像性质

相位是正弦波在时间轴上的偏移量,决定了波形开始的时间点。当 $varphi > 0$ 时,图像向右位移;当 $varphi < 0$ 时,图像向左位移。相位的变化不会 改变波形周期和振幅,但会影响波形在时间轴上的位置。
03 正弦型函数的奇偶性
奇函数性质
奇函数性质
正弦型函数是奇函数,因为对于任意x,都有f(-x) = -f(x)。这意 味着正弦型函数的图像关于原点对称。
对称轴
正弦函数图像关于y轴对称
正弦函数$y = sin x$的图像关于y轴对称,即当$x$取正值和负值时,$y$的值相 同。
余弦函数图像关于x轴对称
余弦函数$y = cos x$的图像关于x轴对称,即当$y$取正值和负值时,$x$的值相 同。
对称中心
要点一
正弦函数图像关于点$(kpi, 0)$对 称
通过调整A、ω、φ的值,可以获 得不同振幅、周期和相位偏移的 正弦型函数。
单位圆与三角函数关系
单位圆是指在平面直角坐标系中, 以原点为圆心、半径为1的圆。
三角函数与单位圆密切相关,单 位圆上的点可以用三角函数来表
示。
在单位圆上,正弦和余弦函数的 值等于点的纵坐标和横坐标的比 值,正切函数的值等于点的纵坐
图像特点
偶函数的图像关于y轴对称,即当 x=0时,y达到最大或最小值。在 x>0和x<0的区间内,函数值相等。
应用实例
偶函数性质在电磁学中有广泛应用, 例如磁场分布等。
既非奇又非偶函数性质
既非奇又非偶函数
性质
正弦型函数既不是奇函数也不是 偶函数。虽然它的图像关于原点 和y轴都有对称性,但它不符合奇 偶函数的严格定义。
振幅与图像高度
常见三角函数图像及性质

常见三角函数图像及性质三角函数在数学中具有重要的作用,主要有正弦函数、余弦函数和正切函数。
这些三角函数的图像及性质对理解三角函数在不同角度下的变化规律至关重要。
1. 正弦函数(Sine Function)正弦函数可以表示为 $y = \\sin(x)$,其中x表示自变量(角度),x表示函数值。
正弦函数的图像是一条波浪形状的曲线,在 $[-\\pi, \\pi]$ 区间内,正弦函数的图像在原点(0,0)处达到最大值1和最小值−1,且图像在x轴上对称。
正弦函数的主要性质包括:•周期性:正弦函数的周期是 $2\\pi$,即 $f(x+2\\pi) = f(x)$。
•奇函数:正弦函数是奇函数,即x(−x)=−x(x)。
•范围:正弦函数的值域为[−1,1]。
•正负性:在第一和第二象限,正弦函数为正;在第三和第四象限,正弦函数为负。
2. 余弦函数(Cosine Function)余弦函数可以表示为 $y = \\cos(x)$,余弦函数的图像是一条类似正弦函数的波浪形状曲线,不过余弦函数的图像在x轴上下移了 $\\frac{\\pi}{2}$。
余弦函数的性质包括:•周期性:余弦函数的周期也是 $2\\pi$,即$f(x+2\\pi) = f(x)$。
•偶函数:余弦函数是偶函数,即x(−x)=x(x)。
•范围:余弦函数的值域为[−1,1]。
•正负性:在第一和第四象限,余弦函数为正;在第二和第三象限,余弦函数为负。
3. 正切函数(Tangent Function)正切函数可以表示为 $y = \\tan(x)$,正切函数的图像是一条周期性的曲线,其在某些角度处会出现无穷大的值。
正切函数的图像在 $x=k\\pi + \\frac{\\pi}{2}$ 时,即 $x =\\frac{\\pi}{2}, \\frac{3\\pi}{2}, \\frac{5\\pi}{2}$ 等,会出现垂直渐近线。
正切函数的性质包括:•周期性:正切函数的周期是 $\\pi$,即 $f(x+\\pi) = f(x)$。
正弦函数的图像和性质

1定义编辑数学术语正弦函数是三角函数的一种.定义与定理定义:对于任意一个实数x都对应着唯一的角(弧度制中等于这个实数),而这个角又对应着唯一确定的正弦值sin x,这样,对于任意一个实数x都有唯一确定的值sin x与它对应,按照这个对应法则所建立的函数,表示为f(x)=sin x,叫做正弦函数。
正弦函数的定理:在一个三角形中,各边和它所对角的正弦的比相等,即a/sin A=b/sin B=c/sin C在直角三角形ABC中,∠C=90°,y为一条直角边,r为斜边,x为另一条直角边(在坐标系中,以此为底),则sin A=y/r,r=√(x^2+y^2)2性质编辑图像图像是波形图像(由单位圆投影到坐标系得出),叫做正弦曲线(sine curve)正弦函数x∈&定义域实数集R值域[-1,1] (正弦函数有界性的体现)最值和零点①最大值:当x=2kπ+(π/2),k∈Z时,y(max)=1②最小值:当x=2kπ+(3π/2),k∈Z时,y(min)=-1零值点:(kπ,0) ,k∈Z对称性既是轴对称图形,又是中心对称图形。
1)对称轴:关于直线x=(π/2)+kπ,k∈Z对称2)中心对称:关于点(kπ,0),k∈Z对称周期性最小正周期:y=sinx T=2π奇偶性奇函数(其图象关于原点对称)单调性在[-π/2+2kπ,π/2+2kπ],k∈Z上是单调递增.在[π/2+2kπ,3π/2+2kπ],k∈Z上是单调递减.3正弦型函数及其性质编辑正弦型函数解析式:y=Asin(ωx+φ)+h各常数值对函数图像的影响:φ(初相位):决定波形与X轴位置关系或横向移动距离(左加右减)ω:决定周期(最小正周期T=2π/|ω|)A:决定峰值(即纵向拉伸压缩的倍数)h:表示波形在Y轴的位置关系或纵向移动距离(上加下减)作图方法运用“五点法”作图“五点作图法”即当ωx+φ分别取0,π/2,π,3π/2,2π时y的值.单位圆定义图像中给出了用弧度度量的某个公共角。
正弦函数、余弦函数的图像和性质

图象的最高点 图象的最高点 与x轴的交点 轴的交点
x
1-
( 0 ,1 ) (2π ,1)
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
π ( π ,0 ) (32 ,0) 2π 2 图象的最低点 (π ,−1) 图象的最低点
-
应用“ 例1.应用“五点法”作图。 应用 五点法”作图。
π
π
例2.分别利用函数的图像和三角函数 先两种方法,求下列不等式的解集:
1 (1) sin x ≥ ; 2 1 5π (2) cos x ≤ (0 < x ≤ ); 2 2
例3.判断y = cos x + 1, x ∈ [0,2π ]与下列 直线交点的个数: 3 ( )y = 2; (2) y = ; (3) y = 0. 1 2
图
y
1-
数、 图
数
图象的最高点 ( ,1) 图象的最高点 2 与x轴的交点 轴的交点
( 0 , 0 ) (π , 0 ) (2π ,0)
x
π
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
2π
图象的最低点 (32 ,−1 图象的最低点 π )
简图作法 (1) 列表 列出对图象形状起关键作用的五点坐标) 列表( (2) 描点 定出五个关键点) 描点( y (3) 连线 用光滑的曲线顺次连结五个点) 连线(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《正弦三角函数的图像和性质》说课稿
尊敬的各位评委老师好!
今天我说课的题目是《正弦函数的图像和性质》,选自高职数学基础模块上册第五章第六单元第一节第二课时。
下面我将从教材分析、教法设计、学法指导、教学过程、板书设计、教学反思等方面对本节课作以简要说明。
一、说教材
1、本节课在教材中的地位及作用
学生在过去已经学习了六种函数,之前还学过三角函数概念、诱导公式等。
在这个时候学习《正弦函数的图像和性质》,一是能让学生更好把握函数的思想,明确研究函数的出发点,二是为以后学习余弦函数、正切函数图像及性质奠定了基础。
因此,本节的内容地位十分重要,它对函数知识的学习将起到了承上启下的作用。
2、学情分析及对策
我所授课的班级学生实际状况是:基础知识相对薄弱,表达概括能力较差,理论联系实际不灵活。
因此我在教学中应运直观的图形,由易到难、由浅入深的教法,有助于学生对知识的理解和掌握。
通过一课时的讲授,指导学生观察,分析、归纳、总结、掌握正弦函数的性质。
3、教学目标
根据中等职业学校数学教学大纲要求,本节课教学内容的结构特征,依据学生学习的心理规律和职业学校学生的实际水平,制定本节课的
教学目标如下:
▲知识目标:
(1)能利用“五点法”作出正弦函数的图像。
(2)理解掌握正弦函数的图像和性质
▲能力目标:
(1)根据正弦函数的性质对正弦函数的图像作出简单的变形应运。
(2)培养学生的观察、分析、归纳和表达能力。
▲情感态度与价值观:在教学过程中让学生体验数学既是抽象的,又是具体的,同时让学生感受数学美,加强学生的美学教育。
4.教学重点、难点
为了使学生能更好学习正弦函数的图像和性质,为以后学习余弦函数、正切函数提供方法保障,因此确定以下重难点。
教学重点:1.能利用“五点法”作出正弦函数的图像
2.理解掌握正弦函数的图像和性质
教学难点:正弦函数图像的简单变形应运
5、教学方法:引导发现法,数形结合法。
二、说教学方法
“教学有法,教无定法,贵在得法。
”根据本节课教学特点,为了更好地突出重点,突破难点,按照学生的认知规律,我将采用的主要教法是:
1、引导发现法:通过一个周期内的正弦函数图像引导得出整个定义域内函数图像的形状和走势,通过观察图形得出出函数性质。
2、数形结合法:数形结合法解决问题直观明了,能把抽象问题简单化,具体化,把正弦函数的性质利用图形表示出来研究时更容易理解和掌握。
三、说学习方法
良好的方法能使学生更好的发挥天赋,而拙劣的方法则可能妨碍才能的发挥。
我认为教师对学生进行学法指导的立足点是从“学会”达到“会学”进而到“乐学”。
本节课我采用的学习方法如下:
1、观察法:学生观察正弦函数图像,让学生去感知图像的最高点与最低点、上升与下降,图像左右延伸,正弦函数的值何时重复出现等。
2、分析归纳法:观察正弦函数的图像,分析图像的变化趋势,归纳出整个定义域内的正弦函数的性质
3、练习法:把本节课所学的正弦函数的性质,针对性的进行练习,以便学生更好的掌握本节课的内容。
四、说教学过程设计:
为了体现出让每个学生都“课有所得”的教学理念,整个教学过程我将从以下几个方面来进行说明:
1、导入新课:
老师直接导入新课,以旧带新,点名课题,自然进入,这样符合学生的思维,也能激发学生的学习兴趣。
2、作函数图像:让学生阅读课本,主要是培养学生使用教材的能力,根据图像总结函数的性质,数形结合解决问题,直观明了,把抽象的问题简单化,具体化,更有助于学生理解和解决问题。
3、例题示范:主要给学生起到示范作用,让学生做题有个模本,养成良好的逻辑思维能力。
4、针对练习:训练学生的模仿能力,动手能力,巩固和加强所学知识,学生对自己所学知识掌握程度有个明确的认知。
5、小结:让学生自己小结,不仅仅是总结知识重要,更重要的是总结数学思想方法。
反馈给老师知道学生掌握知识的程度,反馈给学生知道自己好友那些知识没有掌握。
这样可帮助学生自行构建知识体系,理清知识脉络,养成良好的学习习惯。
6、布置作业:P128——2,3(1)题。
作业是学生信息的反馈,能在作业中发现和弥补教学中的不足。
,
五、说板书设计
板书就是一本微型教案,本节板书为内容板书,目的是直观清晰的理清知识脉络,主要内容是正弦函数的图像和性质
六、说教学反思:
函数问题对于学生来说比较抽象,所以我把这一节内容分成三节来上,这是第二节。
整个教学过程,体现了教师是教材的主导者和创造者,学生是学习的主体。
感觉一节课下来还有很多不如意的地方。
课堂的把控与组织,知识层次的梳理,对学生的引导等,有许多需要改进的地方。
谢谢!
2018年6月5日。
