等腰梯形性质
等腰梯形的特点性质.

等腰梯形的特点性质.
等腰梯形的性质:等腰梯形同一底上的两个内角相等。
两腰相等,两底平行,对角线相等。
等腰梯形中位线的长度是上下底边长度和的一半。
性质有哪些:
1、全等梯形同一底上的两个内角成正比。
2、两腰相等,两底平行,对角线相等。
3、由托勒密定理可以得全等梯形abcd,存有abxcd+bcxad=acxbd
4、等腰梯形对角线的平方等于腰的平方与上、下底积的乘积和。
bd=ac=ab+adxbc=cd+adxbc
5、全等梯形中位线的长度就是上下底边长度和的.一半。
6、等腰梯形是轴对称图形,只有一条对称轴,过上下两底中点的直线即为对称轴。
7、全等梯形的面积公式:s=(上底+下底)×低÷2。
8、特殊面积计算:当对角线垂直时:s=acxbd/2。
八年级等腰梯形的性质PPT课件

2020年10月2日
1
课堂练习 练习三:
求证:等腰梯形的两条对角线相等.
已知:梯形ABCD中,AD//BC,AB=DC
求证:AC=BD
A
D
证明:
∵ AB=DC(已知)
∴ ∠ ABC= ∠ DCB
B
C
(等腰梯形在同一底上的两个底角相等)
∵ BC=CB(公共边)
∴ △ABC≌△DCB(SAS)
∴ A20C20年=10D月2B日(全等三角形的对应边相等)
相等 相等 相等 图形
二、解决梯形问题的基本思路和
方法:通过添加适当的辅助线,把
梯形问题转化为
与
问
题来解决。
2020年10月2日
15
三、等腰梯形常用辅助线的作法:
A
D
A
D
1
B
E
C BE
FC
2020年10月2日
16
执 教:
金南中学 蔡书祥
制 作:
金南中学数学组
孙孝荣
2020年10月2日
17
演讲完毕,谢谢观看!
13
等腰梯形的性质
性质1:等腰梯形在同一底上的两角相等 性质2:等腰梯形的对角线相等
在梯形ABCD中,AD//BC,
∵ AB=DC
∴ ∠ ABC= ∠ DCB
等腰梯形的性质

A
HD
如图7, 延长等腰梯形的两腰 相交于点E,
由∠B=∠C,AD∥BC,可知
△EBC和△EAD都是等腰三角形。
B
图7 F
C 因此从点E作两底的垂线必平分两 底。根据等腰三角形是轴对称图形,
可得等腰梯形也是轴对称图形。过
这也是研究梯形常用的
两底中点的直线是它的对称轴。
辅助线作法,即延长梯
形的两腰交于一点,得
∴ ∠DEC=∠B
∴ ∠B=∠C
等腰梯形的性质1:等腰梯形在同一底上的两个内角相等。
A
D
已知:如图6,在梯形ABCD中,AD∥BC,
AB=DC。
BE
F
图6
求证:∠B=∠C 。
C 证明:过A、D分别作AE⊥BC,DF⊥BC , 垂
足分别为E、F ∴AE∥DF,∠AEB= ∠DFC=900 ∵ AD∥BC
梯形的性质
上面的几幅图中有你熟悉的图形吗?
两组对边分别平行
四边形 只有一组对边平行
平行四边形 梯形
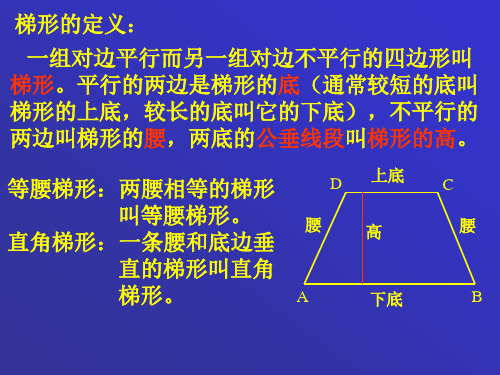
一、梯形 1、梯形的定义:
一组对边平行而另一组对边不平 行的四边形叫做梯形。
梯形
平行四边形
底角 上底
认识梯
腰高
腰
形
下底 底角
一组对边平行,另一组对边 不平行的四边形,叫做梯形。
2、梯形的有关概念:
2.等腰梯形有哪些性质?.
1)等腰梯形的一组对边平行,两腰相等。 2)等腰梯形同一底上的两个底角相等,对角线相等。
3)等腰梯形为轴对称图形,对称轴是连接两底中 心的直线。
3.今天我们在研究梯形问题时,用了哪些方法将梯形问 题转化为其他图形问题? 常用方法有平移一腰、作两高线、延长两腰。
等腰梯形和直角梯形及其性质

艺术创作
在绘画、雕塑等艺术创作 中,等腰梯形和直角梯形 的组合可以创造出独特的 视觉效果和艺术美感。
建筑设计
在建筑设计中,等腰梯形 和直角梯形的组合可以用 于构建独特的外观和结构, 如塔楼、拱门等。
THANK YOU
感谢聆听
详细描述
等腰梯形具有轴对称性,即沿一条经 过两腰中点的直线对折,两侧能够完 全重合。此外,等腰梯形的两个底角 相等,并且两条腰也相等。
面积计算
总结词
等腰梯形的面积可以通过上底、下底和高的长度来计算。
详细描述
等腰梯形的面积可以用公式 `(上底 + 下底) * 高 / 2` 来计算 。这个公式基于梯形面积的一般定义,即“上底加下底后乘 高再除以2”。
02
直角梯形
定义
直角梯形:一个四边形,其中一对相对边是平行的,并且另一对相对边是垂直的 。
定义中的关键词:平行、垂直。
性质
相对边平行
直角梯形的一组对
只有一个直角
直角梯形中只包含一个直角。
面积计算
面积公式
上底
下底
高
面积 = (上底 + 下底) × 高 ÷ 2。
直角梯形在生活中的应用
楼梯设计
直角梯形可以作为楼梯的形状 ,利用其斜边作为踏步,提供 平稳的上下楼梯体验。
斜坡
直角梯形可以作为斜坡的形状 ,用于车辆或人员上下坡的通 道。
排水系统
在排水设计中,直角梯形可以 用于设计沟渠和下水道,以实 现顺畅的排水效果。
等腰梯形与直角梯形的综合应用
01
02
03
机械零件
等腰梯形的性质课件 新人教版八年级下

在梯形ABCD中,AD//BC,
∵ AB=DC
∴ ∠ ABC= ∠ DCB
(等腰梯形在同一底上的两角相
A
D
等)
AC=DB(等腰梯形的对角线
相等)
B
C
小 结:
一、等腰梯形的性质: 等腰梯形 等腰梯形 等腰梯形 等腰梯形是
相等 相等 相等 图形
二、解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转
化为
与
问题来解决。
三、等腰梯形常用辅助线的作法:
A
D
A
D
1
B
E
C BE
FC
执 教: 金南中学 蔡书祥
制 作: 金南中学数学组 荣
孙孝
金南中学欢迎你
课堂练习
练习三:
求证:等腰梯形的两条对角线相等.
已知:梯形ABCD中,AD//BC,
AB=DC
A
D
求证:AC=BD
证明:
∵ AB=DC(已知)
B
C
∴ ∠ ABC= ∠ DCB
(等腰梯形在同一底上的两个底角相 等)
∵ 1:等腰梯形在同一底上的两角相等 性质2:等腰梯形的对角线相等
八年级数学等腰梯形的性质
思
考
1、用一块面积为800 cm 2 的等腰
梯形彩纸做风筝 ,为牢固起见,
用竹条作梯形的对角线,对角
线恰好互相垂直,那么至少需 要竹条 80 cm
A
D
解: ∵四边形ABCD是等腰梯形
∴设AC=BD=x
B
C
又∵AC⊥BD
∴ 1 x 2 = 800
2
解得:x=40
∴至少需要竹条 80 cm
“横断面”的概念
3
S2
5
4
D、S1 = S2
7
练习二
3、如图:若a=4 , b=6 , c=7 ,d=3 , 以它们为边作梯形,其中a∥b , 你认为这样的梯形能作出吗?
若能请作出图形,若不能,
Aa D
c
d
请说明 解: 这样的梯形不能作出
B
Hb C
过A点作AH∥CD 交BC于H点,得到 AHCD
∴AH=CD=d=3 , AD=HC= a = 4
A、m>h B、m<h C、m=h D、不能确定 B 解:
D
h
EC H
2 1 2 1 2 1
∟
过D作DH∥AC交BC 延长线于H点 ∴ BD=DH
∵AC⊥BD
又过D作DE ⊥ BH于E点
∴BD ⊥ DH
∴ DE= BH
又∵ AD ∥ BH , DH ∥ AC ∴四边形ACHD是平行四边形
= (BC+CH)
“横断面”的概念
梯形的性质应用1
横断面
梯形的性思质应用考
2、河流的一个横断面,如图,根据下表中的测量数据计算断面面积
离河一岸的距离(m) 0 2 3 5 9 11
水 深(m)
初中数学等腰梯形的性质知识点详解
初中数学等腰梯形的性质知识点详解初中数学等腰梯形的性质知识点详解对于数学的学习中,下面是对等腰梯形的性质知识点的内容讲解,供大家参考学习。
等腰梯形的性质①两底平行,两腰相等②等腰梯形在同一底上的两个角相等③等腰梯形的两条对角线相等④等腰梯形是轴对称图形,只有一条对称轴,一底的垂直平分线是它的对称轴通过上面对数学中等腰梯形的性质知识点的内容讲解学习,相信同学们已经能很好的掌握了吧,希望同学们会从中学习的更好。
初中数学相关的角与性质知识点详解对于数学的学习中,下面是对相关的角与性质知识点的内容讲解,供大家参考学习。
相关的角与性质相关的角:1、对顶角:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
2、互为补角:如果两个角的和是一个平角,这两个角做互为补角。
3、互为余角:如果两个角的和是一个直角,这两个角叫做互为余角。
4、邻补角:有公共顶点,一条公共边,另两条边互为反向延长线的两个角做互为邻补角。
注意:互余、互补是指两个角的数量关系,与两个角的位置无关,而互为邻补角则要求两个角有特殊的位置关系。
角的性质1、对顶角相等。
2、同角或等角的余角相等。
3、同角或等角的补角相等。
通过上面对数学中相关的角与性质知识点的内容讲解学习,相信同学们已经能很好的掌握了吧,希望同学们会从中学习的更好。
初中数学菱形的定义与性质知识点详解下面是老师对数学中菱形的定义与性质相关知识讲解,希望给同学们的复习学习提供很好的帮助。
菱形的定义与性质1、定义:邻边相等的平行四边形是菱形。
2、性质:(1)菱形的四边形都相等。
(2)菱形的对角线互相垂直,并且每一条对角线平分一组对角,(3)菱形的面积等于对角线乘积的一半。
(4)菱形既是中心对称图形,又是轴对称图形,有2条对称轴。
相信上面对数学中菱形的定义与性质知识的讲解学习,同学们已经能很好的掌握了吧,希望同学们在考试中取得优异成绩。
初中数学梯形定义知识点详解下面是老师对数学中梯形定义相关知识讲解,希望给同学们的复习学习提供很好的帮助。
初中数学 等腰梯形有哪些全等性质
初中数学等腰梯形有哪些全等性质等腰梯形是一个重要的几何形状,在初中数学中学习它的全等性质可以帮助我们更好地理解和应用几何知识。
下面将介绍等腰梯形的全等性质,并解释它们的证明过程。
1. 全等性质1:等腰梯形的两个底角相等。
证明:设等腰梯形ABCD和A'B'C'D'的底边AB和A'B'相等,且底角∠DAB和∠D'A'B'相等。
我们需要证明∠DCB和∠D'C'B'也相等。
首先,连接AC和A'C'。
由于等腰梯形的底边平行,我们可以得知∠ADC和∠A'D'C'是对应角,它们相等。
又因为∠DAB和∠D'A'B'相等,所以∠DAC和∠D'A'C'也相等。
接下来,考虑三角形ADC和A'D'C'。
我们已经知道∠DAC和∠D'A'C'相等,底边AD和A'D'相等,且底边DC和C'D'相等。
根据第一个全等性质(SAS),我们可以得知三角形ADC和A'D'C'全等。
因此,∠DCB和∠D'C'B'也相等。
2. 全等性质2:等腰梯形的两个腿相等。
证明:设等腰梯形ABCD和A'B'C'D'的底边AB和A'B'相等,且腿BC和B'C'相等。
我们需要证明腿AD和A'D'也相等。
首先,连接AC和A'C'。
由于等腰梯形的底边平行,我们可以得知∠ADC和∠A'D'C'是对应角,它们相等。
又因为∠DAB和∠D'A'B'相等,所以∠DAC和∠D'A'C'也相等。
接下来,考虑三角形ADC和A'D'C'。
等腰梯形的对角线有什么性质
等腰梯形对角线的平方等于腰的平方与上、下底积的乘积和,等腰梯形是轴对称图形,只有一条对称轴,过上下两底中点的直线即为对称轴。
等腰梯形同一底上的两个内角相等。
两腰相等,两底平行,对角线相等。
等腰梯形的性质:
(1)两底边相互平行,并且两腰相等
(2)同一底上的底角相等
(3)等腰梯形对角线相等
几何表达举例:
(1)∵ABCD是等腰梯形
∴AD∥BC,AB=CD
(2)∵ABCD是等腰梯形
∴∠ABC=∠DCB
∠BAD=∠CDA
(3)∵ABCD是等腰梯形
∴AC=BD
等腰梯形的判定
1、一组对边相等且不平行,另一组对边平行的四边形是等腰梯形。
2、同一底上的两个角相等的梯形是等腰梯形。
3、对角线相等的梯形是等腰梯形。
4、两腰相等的梯形是等腰梯形
以下判定不作为定理使用:
5、对角线相等且能形成两个等腰三角形的四边形是等腰梯形。
6、对角互补的梯形是等腰梯形。
等腰梯形体积立方计算公式
等腰梯形体积立方计算公式全文共四篇示例,供读者参考第一篇示例:等腰梯形是一种特殊的梯形,其两边边长相等,且上底和下底之间的距离也相等。
计算等腰梯形的体积是一个很常见的问题,通常使用立方计算公式来求解。
在本文中,我将介绍等腰梯形的定义、性质以及如何利用立方计算公式来找到等腰梯形的体积。
让我们来看看等腰梯形的定义。
等腰梯形是一种四边形,其中两条边长相等,被称为等边。
上底和下底之间的距离也相等,被称为梯形的高。
等腰梯形的性质包括:1. 对角线等长;2. 对角线互相垂直;3. 对角线平分角;4. 中点连线平行;5. 上底和下底的平行线段互等长。
接下来,让我们来看看如何计算等腰梯形的体积。
等腰梯形的体积计算公式为:V = (a + b) * h * H / 2,其中a为上底长,b为下底长,h为梯形的高,H为两底的间距。
如果我们有一个等腰梯形,上底长为5cm,下底长为8cm,梯形的高为6cm,两底的间距为3cm。
我们可以将这些值代入等腰梯形的体积计算公式中计算体积,其计算过程如下:V = (5 + 8) * 6 * 3 / 2V = 13 * 6 * 3 / 2V = 78 * 3 / 2V = 234 / 2V = 117这个等腰梯形的体积为117立方厘米。
在实际生活中,等腰梯形的体积计算常常用于建筑、制造业和工程等领域。
在建筑工程中,工程师可能需要计算某建筑物的梯形部分的体积来确定材料的用量,或者在制造业中,生产工人可能需要计算某个零件的体积来确定其重量和成本。
等腰梯形的体积计算是一种常见的数学问题,使用立方计算公式可以很容易地找到等腰梯形的体积。
通过掌握这些知识,我们可以更好地应用数学理论于实际生活中的问题解决,提高我们的数学素养和解决问题的能力。
希望本文能对您了解等腰梯形的体积计算有所帮助。
第二篇示例:等腰梯形是指四边形的两个对边(底边和顶边)长度相等的梯形,通常我们也称之为等腰梯形。
等腰梯形在几何学中具有重要意义,它的体积计算可以帮助我们更好地理解空间的立体形状。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在等腰梯形ABCD中,
∠BAD=∠ADC, ∠ABC=∠BCD,AC=BD
A D
B
C
议一议:
在右下图中,四边形ABCD是等腰梯形,将腰AB 平移到DE的位置。 (1)DE把四边形ABCD分成了怎样的两个图形? (2)图中有哪些相等的线段、相等的角?
A D
B
E
C
研究梯形时,常常移动一腰,把梯形转化为平 行四边形和三角形
(A)
(B)
(C)
┐ (D) (E) (F)
1)如图B那样,两腰相等的梯形叫做等腰梯形 2)如图D那样,一条腰和底垂直的梯形叫做 直角梯形
二.做一做
1.在一张方格纸上作一个等腰梯形(如图) 问题一:图中有哪些相等的线段?有哪些 相等的角? 问题二:等腰梯形是轴对称图形 吗?它的对称轴是什么? A
对称轴
D
结 论 :
1)等腰梯形同一底上的两个 内角相等
2)等腰梯形为轴对称图形, 对称轴是连接两底中心的 直线。
B
C
2.连接等腰梯形ABCD的两条对角线。
问题三:等腰梯形的两条对角 线的长度有什么关系?
A O
D
结 论 :
等腰梯形的两条对角线相等
B
C
二:等腰梯形的性质
等腰梯形同一个底上的两个 内角相等,对角线相等.
D C A D
A
E
F
B
E
B
F
C
例3.已知等腰梯形ABCD,AD∥BC,对角 线AC⊥BD,AD=3cm,BC=7cm. 求梯形的 面积.
四:梯形问题中经常用到的辅助线:
如图示:
随堂练习:
1.已知等腰梯形的一个内角等于70ْ,求其他 三个内角的度数.
2.已知如图梯形ABCD 中,AD∥BC,AB=CD, ∠B=60°,AD=10,BC=18,求梯形的周 D A 长.
三:应用:
例1 如图,在等腰梯形ABCD中,AD=2,BC=4, 高DF=2,求腰DC的长.你有几种方法?
A D A D
B
E
F
C
B
E
F
C
如果将本题改为(1)已知下底、腰、高,求上底; (2)已知上底、下底、腰,求高.你能解决 这个问题吗?说出你的思路.
例2.如图四边形ABCD是等腰梯形, AD=BC, AD=5,CD=2,AB=8,求梯形ABCD的面积
图中有你熟悉的图形吗?
一.看看学学-- 梯形的定义
1.梯形的定义:一组对边平行而另一组对边不平行的四边 形叫做梯形 底 1)平行的两边叫做梯形的底
腰
┐ 底
腰
注意:较短的底叫做上底,较长的底 叫做下底
2)不平行的两边叫做梯形的腰 3)夹在两底之间的垂线段叫做 梯形的高
2练习一.下列图形中,哪些是梯形?(B,C,E)
B
C
学习了本节课,你有什么收获?
1.梯形的定义及类型:
一组对边平行而
四边形 另一组对边不平行
梯形
等腰梯形
直角梯形
2.等腰梯形的性质
(1)两底平行,两腰相等 AD∥BC, AB=CD A D
(2)同底上两角相等 ∠A= ∠D, ∠B= ∠C
(3)对角线相等 AC=BD
B
C
(4)是轴对称图形
