“拍照赚钱”的任务定价-全国大学生数学建模竞赛
拍照赚钱的任务定价数学建模论文
“拍照赚钱”的任务定价分析“通过拍照赚钱”是一种自助服务模式，要求成员在应用程序上收集任务并在完成任务后获得为任务划定的报酬。
在此应用中，任务定价是其核心要素。
通过对“拍照赚钱”任务定价方案的分析，评价和改进，优化任务包装方案，达到了节约成本，提高任务完成度的目的。
对于问题一，通过分析附件一中的任务定价数据，我们可以看到任务评估的平均定价为69.11，任务定价的范围为[65,85]。
在分析未完成任务的原因时，首先，未完成任务的比例为37.9％。
其次，绘制任务完成和任务定价框的折线图。
未完成任务的价格低于已完成任务的价格。
最后，在地图上标记任务的完成。
可以看出，未完成的任务主要集中在区域1中，区域2的完成度最高。
对于第二个问题，选择附件1中的完整数据作为训练集，并将未完成的任务作为测试集。
通过按经度和纬度连接附件I和附件II，建立了以任务定价为因变量的线性回归模型。
利用该模型对原方案中未完成任务的定价进行了预测和分析，预测值为新的定价方案。
新方案的完成率比原方案高11.87％。
对于第三个问题，根据任务位置和成员位置的经纬度信息计算出每个成员到每个任务点的距离，并根据每个成员的任务配额和信誉来分配和打包任务成员，针对问题4和问题4，有必要为附件3中的新项目制定任务定价方案。
首先，从问题3中获得的约束公式用于打包和发布附件3中的数据，可以打包。
到300。
然后，对300组数据进行预测和分析，以获得一组任务定价。
为了知道该方案是好是坏，请进行一系列比较。
利用附件3中的数据，将问题2中建立的模型应用于预测和分析，并获得新的任务定价。
比较两个任务的总价值后，我们发现软件包发布方案的成本较低，因此此结果更为合理。
通过对“拍照赚钱”任务定价的分析，我们可以了解到打包发布任务的成本较低，方案较为合理。
关键词：多元线性回归任务定价任务包装R语言1，问题重述“通过拍照赚钱”是一种自助服务模式，用户可以下载应用程序并成为会员，然后选择执行任务以在应用程序上赚钱。
“拍照赚钱”的任务打包定价模型
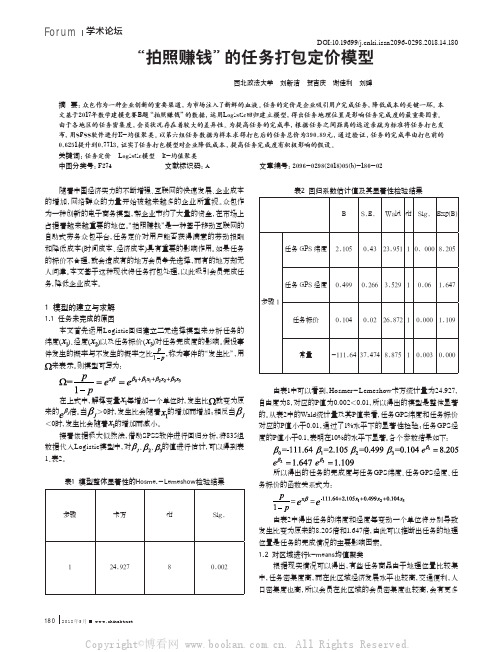
由表1中可以看到，Hosmer－Lemeshow卡方统计量为24.927， 自由度为8，对应的P值为0.002＜0.01，所以得出的模型是整体显著 的。从表2中的Wald统计量及其P值来看，任务GPS纬度和任务标价 对应的P值小于0.01，通过了1%水平下的显著性检验；任务GPS经 度的P值小于0.1，表明在10%的水平下显著。各个参数结果如下：
0.6251提升到0.7713，证实了任务打包模型对企业降低成本，提高任务完成度有积极影响的假设。
关键词：任务定价 Logistic模型 k-标识码：A
文章编号：2096-0298(2018)05(b)-180-02
随着中国经济实力的不断增强、互联网的快速发展、企业成本 的增加，网络群众的力量开始被越来越多的企业所重视。众包作 为一种创新的电子商务模型，帮企业节约了大量的资金，在市场上 占据着越来越重要的地位“。拍照赚钱”是一种基于移动互联网的 自助式劳务众包平台，任务定价对用户能否获得满意的劳动报酬 和降低成本(时间成本、经济成本)具有重要的影响作用。如果任务 的标价不合理，就会造成有的地方会员争先选择，而有的地方却无 人问津。本文基于这种现状将任务打包处理，以此吸引会员完成任 务，降低企业成本。
在上式中，解释变量 每增加一个单位时，发生比 就变为原 来的 倍。当 ＞0时，发生比会随着 的增加而增加；相反当 ＜0时，发生比会随着 的增加而减小。
接着依据极大似然法，借助SPSS软件进行回归分析，将835组 数据代入Logistic模型中，对 、 、 的值进行估计，可以得到表 1、表2。
表1 模型整体显著性的Hosmer－Lemeshow检验结果
文基于2017年数学建模竞赛B题“拍照赚钱”的数据，运用Logistic回归建立模型，得出任务地理位置是影响任务完成度的最重要因素。
“拍照赚钱”的任务定价问题的建模与计算
“拍照赚钱”的任务定价问题的建模与计算作者：杨非非袁晨辉汤仕星邱淑芳来源：《价值工程》2018年第29期摘要：针对“拍照赚钱”的任务定价问题，文章选取了影响任务定价的几个主要因素，研究它们与任务定价之间的函数关系，建立多元线性回归模型和Logistic回归模型，在此基础上分析任务未完成的原因。
然后，利用支持向量机算法引入区域修正参数，得到新的任务定价模型。
最后，依据任务被完成的概率建立最大团“打包”定价模型，从而得到打包后的任务定价方案。
Abstract： For the task pricing problem of "making money by taking pictures"， this paper studies the relationship between the task pricing and its several main influencing factors， and then establishes multivariate linear regression model and logistic regression model to analyze the reason of unfinished tasks. Then， region corrected parameters are introduced by using the support vector machine algorithm and the new task pricing model is obtained. Finally， the maximum group "packing" pricing model is establishedbased on the probability of completing the task， and the "packing"task pricing scheme is obtained.关键词：任务定价；多元线性回归；Logistic回归；最大团；支持向量机Key words： task pricing；linear regression；logisticregression；maximalgroup；support vector machine中图分类号：O29 文献标识码：A 文章编号：1006-4311（2018）29-0194-04“拍照赚钱”是移动互联网下的一种自助式服务模式。
拍照赚钱的任务定价数学建模论文
数学建模论文一，总结内容：（1）用一两个句子说明原始问题要解决的问题；（2）建立了什么模型（数学上属于哪种类型），建模的思想和模型的特征；（3）算法思想（解决思想），特征；（4）主要结果（数值结果，结论）；（回答该主题的所有“问题”）（5）模型和结果检验的优势；关键词模型测试敏感性分析改进普及需求（1）这里必须强调功能和创新；（2）长度（3）确保准确性，简洁性，组织性，清晰度，突出特点和创新；二，提出问题内容：用您自己的语言解释背景，条件和要求；关注“问题”，即需求；要求：（1）不是标题的完整副本（2）根据您的理解，用您自己的语言清楚简洁地说明背景，条件和要求；三，条件假设内容（1）根据主题条件做出假设（2）根据主题要求做出假设；需求（1）理性是最重要的；（2）假设是合理和全面的，但他们不喜欢列出大量不相关的假设，并且不能缺少关键假设；（3）合理假设的作用：简化问题，明确问题并限制模型的适用范围四，象征性协议5问题分析1.名词解释2.问题的背景分析3.问题分析6。
造型抽象要求（1）模型的主要类型：基本模型，微分方程模型，差分方程模型，概率模型，统计预测模型，优化模型，决策模型，图论模型等。
（2）几种常见的建模目的：（对应于（1）的方法）为了描述或解释现实世界中的各种现象，通常使用机制分析方法来探索研究对象的内部规律。
为了预测感兴趣的时间是否会发生或事物的发展趋势，经常使用数学统计或模拟方法为了优化管理，决策或控制事物，有必要合理定义可量化的评估指标和评估方法；（3）建模过程中的几个共同点：模型的总体设计，合理的假设，数学结构的建立，数学表达式的建立；（4）模型要求：清晰，合理，简洁和一般；例如，有些论文没有给出清晰的模型，而只是根据比赛问题给出的特殊情况通过建模方法给出结果。
尽管结果大致正确，但它们缺乏通用性，也不是正确的建模方式；（（对应于第三点））（5）鼓励创新，特别是要欣赏自己的独特和非常规，但要合理（6）避免列出未经评估的一系列模型；具体要求：A.基本模型：首先，必须有一个数学模型：数学公式，方案等；基本模型，完整，正确，简洁B.简化模型：清楚地说明，简化思想和基础；尽可能简化模型。
“拍照赚钱”任务定价分析
一、引言“拍照赚钱”是移动互联网下的一种自助式服务模式，会员从APP上领取拍照任务，赚取对应报酬，帮助企业进行商业信息的搜集和调查[1]。
拍照任务定价是核心问题。
若定价过低，无人领取任务；定价过高，企业成本过高。
本文根据2017年大学生数学建模竞赛B题的样本数据，分析定价的规律和任务未完成的原因，并对已有定价模型起进行优化，以提高任务完成度。
二、定价模型进行频数分析以初步了解价格高低的大致分布状况，可确定65元为任务最低起价，划定定价区间：低价区（价格小于70）；较低价区（价格大于等于70且小于75）；中价区（价格大于等于75且小于80）；较高价区（价格大于等于80且小于85）；高价区（价格大于等于85）。
建立多元线性回归模型分析价格规律，令价格为被解释变量，影响因素为解释变量，影响程度为回归系数。
下面根据样本数据确定这些影响因素所代表的解释变量及其对应的回归系数。
（一）“地理位置”（x1）问题背景提示任务多关于商业数据的收集，任务发布的密集地即是商业区的聚集地，应是城市的中心地区。
根据样本数据的经纬度作散点图，观察发现：低价区在地理位置上分布密集且聚集明显，与城市中心区有关联。
交通便利、人流密集的城市区，完成任务的成本和花费相对于交通不便的乡镇区更低，任务接受者更偏好于接受城市区的任务，即能够以相对更低的价格接受发布在城市的任务。
由如上分析可得：越靠近城市中心点，定价越低；离城市中心点越远，定价越高。
低价区任务点的分布提示城市区的分布，低价区任务点的分布边缘提示城市和乡镇的边缘。
确定“地理位置”为第一个解释变量（x1），将任务点按照地理位置划分为“城市区”和“乡镇区”。
观察散点图发现低价区呈三个中心不同的聚集区趋势，用K均值聚类分析对低价区任务点分成三个区域，等同于三个城市区，三个中心对应三个城市中心点的经纬度（23.102063490780132，113.27916890673757）、（22.97700771477778，113.75894413666668）、（22.62107796724637，114.00599721014495）。
2017数学建模B题问题1解析——“拍照赚钱”的任务定价
【 关键词】 拍照赚钱 ； 多元 回归分析 ； 插 值与数据拟合 【 基金项 目】 ２ ０ １ ７年 陕 西省 教 育厅 科 学研 究项 目（ 编
号： １ ７ Ｊ ＫＩ １ ７ ７） ．
依据最ｄ ｘ Ｚ－ 乘法原理 ， 借助 Ｓ Ｐ Ｓ Ｓ软件对 ｎ ． ， ｎ ： ， 的值
随 着信 息 时代 的进 步 ， 智能手 机的像素越 来越 高 ， 拍 照 也 从 数 码 相 机 过 渡 到 了手 机 ， 手 机 不 仅 可 以拍 出生 活 照 、 风 景照等 ， 它还可 以用来拍照赚钱 ， 只要你 的手机 能拍 出清 晰 进行估计 ， 可 以得 到 表 ｌ 一 表３ ．
一． ３ ８ ８ 一ｌ ５１ ． ６ ４ ０ ． ｏ ｏ ｏ ． ３ ２ ４ １ ２ ８． １ ２１ ． Ｏ ０ ｏ
ｔ
Ｓ ｉ ｇ ．
４ ２ ９ ９ ． ７ ０ ９ ２ ２ ． ３ １ ６ ． Ｏ ｏ ｏ
． ０ ０ ４ ． １ ５ ０ ５ ４ ９
＝
ｄ ｘ ｚ． 乘法求解参 数． 以二 阶线性 回归模型为 例 ， 求 解 回归 参
数 的标 准 方 程 组 为
０． ４ ４７．
所 以任务定价 与 Ｇ Ｐ Ｓ纬度 、 Ｇ Ｐ Ｓ经度 、 任务执行情况 的
函数 关 系式 为
Ｙ ＝一０ ． ０ １ ８ ｘ ｌ一０ ． ５ ４ ９ ｘ ２＋１ ９ ． ２ ２ ６ ｘ ２＋４ ． ７ ２ ９ ． （ １ ）
残 差 ８ ． １ ６ ６ Ｉ ｏ ８ ９ ２ ６ ２ ９ １ ４ ８ ３ １ ． ８ ９ ８ 总计 １ ． ４ ７ ７ “ ８ ９ ２ ６ ５
． ｏ ｏ ０
因． 任务 Ｇ Ｐ Ｓ经纬 度与价 格 、 用户 是否 下载使 用 Ａ Ｐ Ｐ存 在 着 非 常 强 的相 关 性 ． 问题 １ ： 建 立 执 行 任 务 情 况 与 三 个 自变
2017数学建模高教杯全套
2017年高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）A题CT系统参数标定及成像CT(Computed Tomography)可以在不破坏样品的情况下，利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像，由此获取样品内部的结构信息。
一种典型的二维CT系统如图1所示，平行入射的X射线垂直于探测器平面，每个探测器单元看成一个接收点，且等距排列。
X射线的发射器和探测器相对位置固定不变，整个发射-接收系统绕某固定的旋转中心逆时针旋转180次。
对每一个X射线方向，在具有512个等距单元的探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量，并经过增益等处理后得到180组接收信息。
CT系统安装时往往存在误差，从而影响成像质量，因此需要对安装好的CT系统进行参数标定，即借助于已知结构的样品（称为模板）标定CT系统的参数，并据此对未知结构的样品进行成像。
请建立相应的数学模型和算法，解决以下问题：(1) 在正方形托盘上放置两个均匀固体介质组成的标定模板，模板的几何信息如图2所示，相应的数据文件见附件1，其中每一点的数值反映了该点的吸收强度，这里称为“吸收率”。
对应于该模板的接收信息见附件2。
请根据这一模板及其接收信息，确定CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向。
(2) 附件3是利用上述CT系统得到的某未知介质的接收信息。
利用(1)中得到的标定参数，确定该未知介质在正方形托盘中的位置、几何形状和吸收率等信息。
另外，请具体给出图3所给的10个位置处的吸收率，相应的数据文件见附件4。
(3) 附件5是利用上述CT系统得到的另一个未知介质的接收信息。
利用(1)中得到的标定参数，给出该未知介质的相关信息。
另外，请具体给出图3所给的10个位置处的吸收率。
(4) 分析(1)中参数标定的精度和稳定性。
在此基础上自行设计新模板、建立对应的标定模型，以改进标定精度和稳定性，并说明理由。
2017数学建模B题评阅要点
2017高教社杯全国大学生数学建模竞赛B题评阅要点
本要点仅供参考，各赛区评阅组应根据对题目的理解及学生的解答，自主地进行评阅。
本题来源于实际问题，要求对“拍照赚钱”项目中的任务进行定价，使得任务对会员有吸引力而不至于被会员所放弃，特别是那些处在比较偏远位置的任务。
问题1：在已经结束的项目中研究任务定价规律，分析任务未完成的原因。
理论上任务定价跟所有会员的限额、会员与任务之间距离有关，在已知的定价数据上，这是一个高维数据函数拟合问题，需要一定的降维处理；同样，任务是否完成也跟所有会员的限额、会员与任务之间距离有关，在已知任务完成与否的情况下，这是一个高维数据分类问题。
问题2：问题2要求对已结束项目中的任务设计新的定价方案。
不同的原则可能对应于不同的定价，一个好的定价方案应该考虑到以下几点：
1.任务定价的主要目的是在不提高平台的运行成本的前提下，尽量提高任务的
完成率。
2.定价方案应该对所有会员都有一定的吸引力，均衡性是一种可能的方案；
3.定价方案需要照顾到优质会员的利益，也要对新会员保留一定的机会；
对定价方案的评价可以模拟会员抢单，统计任务完成率进行评价。
问题3：问题3是考虑任务打包问题，按照一定的原则打包（比如就近打包和远近搭配打包等方式），在保证任务完成率的情况下节省成本也可以作为一个评价定价方案的新维度。
问题4：问题4就是将前面问题2和问题3的方案应用到实际任务之中，需要通过模拟用户抢单，统计任务完成率来对方案进行评价。
评阅时主要关注模型的合理性和正确性。
2017年数学建模B“拍照赚钱”的任务定价模型
“拍照赚钱”的任务定价模型摘要本题要求分析“拍照赚钱”任务的服务模式，研究其定价规律，并设计新的任务定价方案，结合实际情况，修改定价模型，最终对新项目设计任务定价方案，并评价方案的实施效果。
求解的具体流程如下：针对问题一：为了研究项目的定价规律，分析任务未完成的原因，利用附件一的信息，在地图上定位所有坐标的位置，发现任务集中在广东、东莞、佛山、深圳四市，分别标明每个城市的成功任务和失败任务。
以深圳为例，对深圳市任务进行聚类分析，结果分成5类，由相应任务的定价可以得出，人口密集处定价较低，人口稀少处定价较高的定价规律。
将附件二的位置信息同理在地图上定位，分别计算任务周围的会员数，分析其与定价的联系。
针对问题二：由问题一结果可知，任务定价与任务周围人数和任务周围人口密度等因素有关。
利用网络爬虫爬取广州、东莞、佛山、深圳四市医院，学校，小区，超市四种人口密度较大场所的经纬度，统计成功任务周围十公里人口密集场所。
用RBF神经网络模型，从而确定新的定价方案。
将此方案与原方案进行比较，得出两种定价方案的差异。
针对问题三：为了解决用户争相选择位置集中任务等问题，可将多个任务联合打包，以便用户更好得执行任务。
利用问题二中RBF神经网络模型求出新的定价方案下的任务定价；同问题一，求任意两个任务之间的距离。
当两个任务之间的距离小于一定值时，便可将这两个任务种做打包处理。
对于打包的任务，可将每个任务的定价结合附近会员的信息求出最终定价；对于未打包的任务，任务定价不变。
针对问题四：为了对新项目设计定价方案，并评价方案的实施效果，将新项目中任务的位置定位于地图上，可以发现任务集中分布于两个区域，且两个区域距离较远，可认为互不影响。
结合前面问题的分析，可知任务定价与区域的经济发展情况和用户到任务的距离有关。
对用户而言，用户将优先选择距离较近且定价较高的任务，因此，可以使用灰度关联分析的方法，建立不同任务对会员的吸引力，从而对定价方案做出评价。
2017年全国大学生数学建模竞赛A题一等奖
针对问题二，需制定新的任务定价计划，属于优化问题，解决该问题需找到 每个任务的最优定价。由附件一可知任务标价与位置和执行情况都有关，故可按 距离关系和任务完成率分别制定一组定价计划。按距离制定的计划，关键在于距 离会员近的任务定价低些，而距离会员远的任务定价则按一定比例高些。由问题 一得到定价按位置大致分为几类，将任务按这几类划分区域，分别算出各区域内 每个任务的最优定价。按任务完成率制定的计划，关键在于新计划定价与任务执 行情况之间的关系，可用 0-1 整数线性规划建立相应模型求解。最后，分别计算
2
在原计划和两组新的定价计划下，该平台一组项目需支付的总定价，比较其值大 小。三者中总定价少且任务完成率高的计划为最优定价计划。
针对问题三，只需考虑任务位置与定价之间的关系，故在问题二按距离关系 所建立的定价计划的基础上做出改进即可。先将原来的 835 个任务按距离进行聚 类分析，利用可打包任务间的距离范围确定聚类个数。对于仍是未打包的任务（单 个任务）而言，定价不变；对于打包在一起的多个任务，可整体看成一个任务， 聚类的中心即这个新任务的位置，即从问题二中的点与点之间距离变成点与集合 之间的距离。题目中提到会员之间对任务有竞争关系，则此时的距离不再是任务 与最近会员间的距离，此距离还与时间有关，可以基于序贯算法（优先级的先后 次序）来改进定价模型。首先，对打包后的任务集合以会员能接受的最远距离为 半径画圆，得到可能会竞争这个任务集合的会员集合。其次，每个会员都有其任 务预定限额，若该任务集中任务个数超过某个会员的限额数，则该会员失去竞争 力，从而缩小会员集合。每个会员的任务开始预定时间也不相同，挑选预定时间 最早的会员得到进一步缩小的会员集。最后，在上述会员集中按问题二的定价模 型，找到与该任务集距离最短的会员，则这个任务集就被这个会员所领取了。按 上述算法思想来修改问题三种按距离关系建立的定价计划。另一方面，打包后会 员可选择的总任务数减少，之前由于距离太远未被选择的任务可能会因此被没有 抢到任务的会员选择，导致任务完成率增大；而打包被领取的任务的完成情况不 受打包的影响。因此，整体任务完成率增大。
2021年国赛建模b题
“拍照赚钱〞类软件任务定价规律的探讨与改进方案分析摘要随着互联网技术的开展，人们在经济水平飞速开展的同时，各种观念也在不断变化；例如互联网技术已通过其庞大的用户量及强大的执行效率使得许多曾需要专人投入大量本钱的传统行业趋于群众化、分散化。
例如最近市场上新兴的“拍照赚钱〞软件，它利用人们的零散时间随时随地拍照赚钱，备受群众青睐。
然而该类软件仍然存在定价不合理、任务完成度不高等阻碍该类软件开展的瓶颈。
本文通过对客户与任务位置、完成任务收益等变量进行数学模型分析，提出了一些比该类软件现行运作模式更科学、更高效的方案。
第一问中，为确定现有定价方案的问题，我们以任务分配范围内不同的城区作为根本单位，将任务根据定价分为三份，并通过建立线性回归方程了解了各客观变量对定价产生的影响，再通过对失败案例的因子分析找到了导致失败的变量及它们对失败变量的影响程度。
第二问设计新方案时，以为拍照赚钱平台带来最大利润为根本目的，将现有方案与变量间相互作用情况相似的垄断性市场中打车平台收费方案进行类比，分析并一一对应相应的变量关系，再通过现有的对打车平台获利最大值计算的模型变量的类比得出新方案。
第三问中，通过聚类分析可以将5个相聚较近的变量进行“打包〞。
“打包〞的点即为包点，将其代入第一问中地址相关信息，可求出打包后每个地区所具有的“包点〞的个数，再由第二问公式问求出定价，并与原始结果进行对照。
第四问中，将所给密集数据视为在同一点进行“打包〞，求出打包结果所在点的GPS并代入第一问中的值关键词：自然区域分区、多项线形回归预测、因子分析、类比、Curve Fitting Tool、聚类分析、一、问题重述随着科技日新月异的开展，人们获取钱财的方法越来越多，“众包〞一词也出现在群众视野。
众包指的是一个公司或机构把过去由员工执行的工作任务，以自由自愿的形式外包给非特定〔而且通常是大型的〕群众网络的做法。
众包的任务通常是由个人来承当，但如果涉及到需要多人协作完成的任务，也有可能依靠开源的个体生产的形式出现。
2018全国大学生数学建模竞赛“拍照赚钱”
从企业的角度，当然希望报酬（定价）越低越好，但是会员期望自然是越高 越好。当价格较高时，企业负担较重而任务完成较好；价格较低时，会出现所需 信息收集偏少的情况。当价格在双方之间相对平衡时，所需信息就能够比较好的 满足企业需求，同时企业的支出又在可以接受范围内。
近期，某 APP 针对珠三角的广州、东莞、深圳和佛山四地进行了一场调研。 虽然该 APP 拥有的注册会员人数远远超过任务数，但是这一任务的完成率非常 低，而且不同地域的完成率差异非常显著。特别是在市场巨大的两个城市，获取 的信息非常少，从而导致获取的数据无法对于进一步的企业行为进行指导。
同时，在任务完成不好的地区，又拥有非常多的注册会员。因此，一个比较
2
明显的问题就是任务支付的报酬偏低。但是，对于企业，如果通过提高这些地区 的服务报酬，就增加了企业的负担。如何通过价格调整，保证后续任务较高的完 成率又不增加企业负担，就是 APP 运营商面临的问题。
1.3 需要解决的问题 对于运营商而言，重新制定价格并要保证企业以及会员的双赢，仅仅通过一 些经验的判断还不够充分。如果能够在历史数据的基础之上，对于价格的调整、 任务的发布进行一些定量分析，并提出一些定量的调整策略，那将对于后续任务 完成率起到非常大的帮助。 首先，本文要在历史数据的基础上，进一步寻找低任务完成率地区的定价、 任务数、会员数与其他数据的关联。其中关联的数据包括当地经济水平、物价指 数等，这是因为这些指标对于会员的预期报酬紧密相关。通过对比，判定出不同 地区的相对价格高低，并与现有定价方式比较，分析得到一些结论，为进一步的 价格调整提供定量参考并修正现有的定价方案。 其次，APP 运营商也有一些其他提高会员个人收益的设想。实际上，有许多 会员可同时接受好几个任务并且完成的非常不错，并且已经有一些现成的统计数 据。如果几个任务距离很近但同时被一个会员接受，那么他就可以在交通方面花 费较少时间完成几个任务，完成单个任务的平均时间就会缩短。这样即使单个任 务价格稍低，会员也会乐意同时接受几个邻近地区的任务。如果价格不是太低， 该会员的平均收益率还是可以接受的。如何结合地域、会员个数、会员可承担任 务最大值、会员信誉度等进行任务打包发送，是本文要解决的另一重要问题。 最后，对于这些方案的合理性，还将进行数值仿真。一方面，在历史任务中， 将调整过后价格分布与任务未完成情况对比，对于预期完成率给出一个直观的刻 画。其次，对于新的任务，依据新的定价方案，将任务进行打包发送，并给出相 应定价方案。此外，还将深入分析有关不足，为进一步价格调整做好准备。
“拍照赚钱”APP中任务定价问题分析及求解
对原 有 的定 价机 制进 行改 进 并 结合 会 员 的分 布情 况， 信 誉值 等 因素 ， 给 出优 化 的 任 务分 配 方 案 ， 实 现 以最 低 成本 取得 更高 任务 完 成率 。
合分析伪 。 最后 ． 将未完成 的任务单 独提
取， 从任务的
分布和定价 、 当地 的会 员信 息 、 任务分 布区域 的经 济状 况、 交通因素等方面 ． 分析任务 的完成情况
中． 导 致用 户会 争相选 择 ． 一 种 考虑 是将 这些 任 务联 合在 一起 打包发 布 。在这种 考虑下 ， 如何 修改前 面 的
图 １ 未 完 成 和 已 完 成 任 务 分 布 图
图 １中展 示 了任 务 依 据 坐 标 位 置 在 地 理 七的
呈现 ． 其中红色圆点表示未完成任 务． 黑 色 表 示 已 完成任务 ， 通偶 对该 图 的 观 察 ， 发 现 黑 色 的 点 即完 成 的任 务 呈 聚 集状 态 ． 并 且 聚 集 中心 主 要 分 布 在 城
最 高 是本 文 的研 究重 点 ， 、 关 键词 ： 任务定价 ； 优 化 问题 ； 最低成本 ； 最 高 完 成 率
中图分类号 ： ＴＰ １ ３ ９
根据 题 目信息 ． 可知“ 拍 照 赚钱 ” Ａ Ｐ Ｐ中 的任 务 定价 、 任 务分 配不 尽合 理 。部 分任 务 无人 问 津 ． 某 些
完 成率 ． 并 且呈 负 相关
括 任 务 地 点 的 经
度、 纬度 、 任务标 价 和完 成情 况 。首先 ， 需要 明确 ， 任 务 的 位 置 是 如 何 影 响 其 定 价 的 可 以利 用 Ｅ Ｘ Ｃ Ｅ Ｌ 以及 Ｂ Ｄ Ｐ应用 程序 将 全 部 任 务 的 信 息 以 散 点形 式 在 地 图 上表 现 出来 ． 利 用不 同颜 色 区分 完 成 与 未 完
拍照赚钱任务定价模型(2017年全国大学生数学建模大赛B题)-国家二等奖论文
将该式定义为一致性指标，CI=0时A为一致阵；CI越大A的不一致程度越严重， 所以CI相当于除 外其余n-1特征根的平均值。为衡量CI的大小，引入随机一致 性指标RI，形成A,计算CI既得RI。如表3
3 成对比较矩阵和权向量 元素之间两两对比，对比采用相对尺度，设要比较各准则C1，C2，C3...,Cn
对目标的重要性
A (aij)n n, aij 0, aij 1/ aij
C1,C2,...,C4 依次表示 6 个是否完成影响因素：会员密度、交通情况、任务 位置、价格、任务难度和信誉度 6 个准则，用成对比较法得到准则层对目标的成 对比较阵：
1
815
.000 72.435
1.624
1
815
.000 69.468
-.034
2
814
.000 67.418
4.032 30.138
3
813
.000 65.619 51.044 -259.841 493.254
1
815
.000 66.682
1.233
1
815
.000 72.347
.023
1
815
.000
4.239
.000
1
815
.000
4.200
.209
1
815
.000 66.682
.209
1
815
.000
.015
.811
自变量为 距市区距离。
4
图 3 任务标价关于任务点距市区的距离拟合图
由表 2 的 R2 可知，通过任务标价关于任务点距市区的距离拟合出的函数中三 次函数的贴合度最大，因此选取三次函数进行分析。根据表 2 可知任务标价 y 关 于任务点距市区的距离 x 的三次函数如下：
2017全国大学生数学建模B题
“拍照赚钱”定价分析随着现代互联网技术发展“拍照赚钱”已经成为时下一种热门的互联网自助模式，如何对任务进行定价的合理性显得尤为重要，本文针对题目重所给的信息数据进行归纳设计和总结，研究其定价规律，并建立模型。
针对问题一，本文对附件数据进行分析，将会员点在地图中标出，发现任务点集中在佛山，广东，深圳，东莞四个城市的会员进行聚类分析。
对数据进行线性回归分析，结果表明，任务的定价与周围用户的限额总量，周围用户的平均距离都与会员点的分布有很重要的关系。
最后通过比较未完成任务与已完成任务的相关矩阵得出距离对任务的完成的影响是显著的。
针对问题二，设计新的任务定价方案是一个优化问题，以最小成本完成最大化，将附件中数据在地图中展示，我们综合考虑任务情况与会员分布的互相影响，即任务对于周围的会员存在着吸附力ci = f(s,d)，它与任务价格正相关，与距离任务距离负相关问题重述1.1 问题背景随着互联网+的发展，许多产业逐渐发生偏移，传统工作方式在互联网的渗透下，不再是自己传统的工作模式，工作人员不再限制，工作地点不再固定在一个位置，增加了人群就业，提高了工作效率。
国家也积极发展众包，即汇集众力增加就业，借助互联网发展，将特定的工作不再局限于一部分人，而是面向自愿参与大众人群，最大限度利用大众的力量，提高某些传统工作的效率，降低成本的投入。
‘‘拍照赚钱’‘便是面向大众的一种众包方式，最大限度的利用人力提高工作效率，用户下载APP，注册成为app的会员，然后在APP上领取拍照任务，完成在APP领取的任务，赚取佣金。
拍照赚钱的这一种方式，对于市场调查等一类工作有很大的帮助，减少了调查的时间，缩短了调查的周期。
可以在很短时间内完成一项调查的工作，提高任务完成的效率。
而且可以保证数据的真实性。
但是，app中的任务定价是核心要素。
定价的合理是否会影响任务的完成情况。
二丶问题分析2.1 问题一问题一需要分析出附件一中未完成任务的原因，问题一中我们对于未被完成的任务先进行三方面的分析。
2017年数学建模B题问题一与问题二解析——“拍照赚钱”的任务定价模型
现代商贸工业2017年数学建模B题问题一与问题二解析—“拍照赚钱”的任务定价模型张姣丽杨荣庆钟芸(西南大学商贸学院，重庆402460)摘要：拍照赚钱APP”是基于移动互联网下的一种信息共享平台，其成功与否与任务发布者的出价密切相关。
基于此，主要研究其的任务定价问题，采用多元线性回归模型，借助SPSS软件处理数据，并通过分析任务所在的经度、纬度、任务完成情况三个影响因素对任务定价的影响。
此外，借助插值和拟合模型求出原方案的拟合函数，利用MAT-LAB计算出定价的理想值，并设计新的定价方案，利用 AHP和原方案进行比较，得出新方案优于原方案。
关键词：任务定价；多元线性回归模型；插值与拟合模型；AHP中图分类号：G4 文献标识码：A d oi：10. 19311/k i.1672-3198. 2018. 05. 085“拍照赚钱”是一种基于移动互联网络的自助式劳务众包平台，其成功与否与任务发布者的出价密切相关，因而任务定价成为该平台的运行核心。
根据数据信息剔除附件一的异常数据，筛选出有效信息。
1问题一的模型建立与求解1.1确定影响因子分析附件一的数据，任务定价作为因变量，其它因 素作为影响因子，即：(1) 任务GPS纬度。
(2) 任务GPS经度。
(3) 任务执行情况。
利用M A T L A B得出图1。
图1任务定价与任务GPS纬度，任务GPS经度3D散点图1.2模型的建立与求解多元线性回归分析一般模型为:水平。
3.2.2 组建教师微课制作团队，构建会计微课资源体系为实现微课教学的教学实效性，就需要积极组建教师微课制作团队，构建会计微课资源体系。
首先对教师团队进行合理分工，然后讨论确定每门课微课选题，主要从章节重难点内容进行微课制作，通过合理、精确选题，更好地解决传统教学中不能解决的教学问题；构建各种微课资源群，学生可根据自己的实际学习情况，有侧重点地进行巩固学习；其次将制作的微课运用到会计教学中，做好精品课程的教学设计，培养一批勤于实践探索、善于反思总结、乐于奉献的科研型骨干教师，从而提高整体教学水平，推进学校的教学改革。
数学建模b“拍照赚钱”的任务定价模型
“拍照赚钱”的任务定价模型摘要本题要求分析“拍照赚钱”任务的服务模式，研究其定价规律，并设计新的任务定价方案，结合实际情况，修改定价模型，最终对新项目设计任务定价方案，并评价方案的实施效果。
求解的具体流程如下：针对问题一：为了研究项目的定价规律，分析任务未完成的原因，利用附件一的信息，在地图上定位所有坐标的位置，发现任务集中在广东、东莞、佛山、深圳四市，分别标明每个城市的成功任务和失败任务。
以深圳为例，对深圳市任务进行聚类分析，结果分成5类，由相应任务的定价可以得出，人口密集处定价较低，人口稀少处定价较高的定价规律。
将附件二的位置信息同理在地图上定位，分别计算任务周围的会员数，分析其与定价的联系。
针对问题二：由问题一结果可知，任务定价与任务周围人数和任务周围人口密度等因素有关。
利用网络爬虫爬取广州、东莞、佛山、深圳四市医院，学校，小区，超市四种人口密度较大场所的经纬度，统计成功任务周围十公里人口密集场所。
用RBF神经网络模型，从而确定新的定价方案。
将此方案与原方案进行比较，得出两种定价方案的差异。
针对问题三：为了解决用户争相选择位置集中任务等问题，可将多个任务联合打包，以便用户更好得执行任务。
利用问题二中RBF神经网络模型求出新的定价方案下的任务定价；同问题一，求任意两个任务之间的距离。
当两个任务之间的距离小于一定值时，便可将这两个任务种做打包处理。
对于打包的任务，可将每个任务的定价结合附近会员的信息求出最终定价；对于未打包的任务，任务定价不变。
针对问题四：为了对新项目设计定价方案，并评价方案的实施效果，将新项目中任务的位置定位于地图上，可以发现任务集中分布于两个区域，且两个区域距离较远，可认为互不影响。
结合前面问题的分析，可知任务定价与区域的经济发展情况和用户到任务的距离有关。
对用户而言，用户将优先选择距离较近且定价较高的任务，因此，可以使用灰度关联分析的方法，建立不同任务对会员的吸引力，从而对定价方案做出评价。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M
N
Q Q
四. 问题分析
4.1. 问题一分析 问题一要求我们探索定价规律及研究任务未完成的原因。 从系统角度出发考 虑每个任务的定价有两个方向：任务与用户的关系、任务与任务的关系。从这两 个角度考虑，我们可以进一步分析任务与用户的关系主要有任务周围用户数量， 任务周围用户密度等；任务与任务之间的关系主要为任务的离群程度。 我们可以对以上因素量化， 并分别将定价与以上因素进行函数拟合，利用拟 合度判断定价是否与以上因素有关。 接着根据有关的因素对完成的任务与未完成 的任务分别进行分析，判断任务未完成的具体原因。 4.2. 问题二分析 问题二要求我们设计新的任务定价方案，并和原方案进行比较。这是一个博 弈问题的优化，博弈双方是定价与成功率。我们的目标是成功率尽可能高，定价 尽可能低。成功率除了与定价有关，还与问题一中的若干影响因素有关。我们可 以回归分析得到成功率关于以上因素的函数关系。 接下去可以建立优化模型并求解。根据给出的数据集，我们寻找成功执行的 任务定价与未成功执行任务的定价之间的差距，并寻找合理的定价区间。以该区 间为约束， 分别就成功率最高及定价总和最低为目标，将其划分为两个优化模型 并求解能得出总定价固定的情况下成功率最高的定价方案以及成功率固定总定 价最低的定价方案。 得出方案后可以就成功率与定价与原方案进行对比来判断新 定价获得的效果。 4.3. 问题三分析 问题三要求考虑多任务打包发布，修改定价并分析对任务完成情况的影响。 由于本题任务点分布不均匀，我们考虑对 DBSCAN 算法进行改进：算法的半径 改为得分半径，成功率高的点得分高，成功率低的点得分低。为了提高成功率， 我们将成功率低的点与成功率高的点打包。打包后还需要分析打包的合理性，即 打包任务周边会员的信誉、限额等因素，如果合理就保留该包，不合理就打散该任务本身价值、 路途花费。即任务打包后任务的本身价值不变，但由于路途花费（包括时间、交 通费用）减少，在系统定价时打包的任务总价低于原定价总和。根据原数据找到 任务本身价值、路途划分、总定价三者的关系，再根据问题二得到的优化模型进 行最优定价搜寻，最终可以对比打包前后成功率的变化情况来体现打包的效果。 4.4. 问题四分析 问题四给出了一个新项目，要求给出我们的定价方案及评估方案实施效果。 将数据代入问题二得到的定价模型以及问题三得到的打包模型进行求解， 输 出每个任务定价与成功率数据，并对结果进行分析。
符号
dij
符号含义 任务周围用户密度 用户 i 距离任务 j 的距离 任务周围最近若干个用户离该任务的距离均值 任务离群度 任务定价 一定范围内用户限额总和 第 i 个任务的定价 第 i 个任务的成功执行率 任务总价 任务平均成功执行率 商家给系统的定价 系统给用户的定价
2
d ave O
p
s Pi Si
4.
二. 模型假设
1. 假设会员到所有任务点的出行便利程度一致，到达任务点所用时间随距离增 加而增加，且该距离为直线距离； 2. 不考虑天气等原因对会员出行的影响； 3. 所有任务的难度相同，即不考虑任务难度对会员选择造成的影响； 4. 每个任务至多由一个人完成，不考虑多人合作完成一个任务的情况。
三. 符号说明
关键词：LOF 离群因子；回归分析法；多目标优化；DBSCAN 算法；众包定价
1
一. 问题重述
1.1. 问题背景 “拍照赚钱”是移动互联网下的一种自助式服务模式。用户下载 APP，注册成 为 APP 的会员，然后从 APP 上领取需要拍照的任务（比如上超市去检查某种商 品的上架情况） ，赚取 APP 对任务所标定的酬金。APP 中的任务定价是该平台运 行的核心要素，如果定价不合理，有的任务就会无人问津，而导致商品检查的失 败。 1.2. 数据集 附件一是已结束项目的任务数据，包含了每个任务的位置、定价和完成情况 （“1”表示完成， “0”表示未完成） ； 附件二是会员信息数据， 包含了会员的位置、 信誉值、 参考其信誉给出的任务开始预订时间和预订限额， 原则上会员信誉越高， 越优先开始挑选任务， 其配额也就越大（任务分配时实际上是根据预订限额所占 比例进行配发） ；附件三是一个新的检查项目任务数据，只有任务的位置信息。 1.3. 问题要求 1. 2. 3. 根据上述题目背景及数据，题目要求建立数学模型讨论以下问题： 研究附件一中项目的任务定价规律，分析任务未完成的原因。 为附件一中的项目设计新的任务定价方案，并和原方案进行比较。 实际情况下，多个任务可能因为位置比较集中，导致用户会争相选择，一种 考虑是将这些任务联合在一起打包发布。在这种考虑下，如何修改前面的定 价模型，对最终的任务完成情况又有什么影响？ 对附件三中的新项目给出你的任务定价方案，并评价该方案的实施效果。
“拍照赚钱”的任务定价
摘要
在“拍照赚钱”的新自助式服务模式下，用户可领取 app 上的任务，成功执行 便可赚取标定的酬金。 在这种模式下，如何合理定价从而获取最高收益成为了系 统运营的核心。 本文针对题中所给的数据信息进行数据挖掘，设计了一套较为合 理的定价及任务打包算法。 问题一中，我们首先猜测了可能影响任务定价的因素，包括：任务周围的用 户限额总量、任务周围的用户密度、任务的离群程度等。我们量化以上可能的影 响因素， 并以该因素为自变量以定价为因变量回归分析，通过拟合度来判断该因 素是否对定价有决定作用。我们随机抽取 70%的数据进行回归训练，结果表明， 任务的定价与周围用户的限额总量、周围用户的平均距离、自身的离群程度关系 密切。 利用剩余的 30%数据分别对以上回归方程进行检验， 用均方残差偏移程度 来评价方程的可靠性。 根据三个因素，对于成功执行的任务与未成功执行的任务 分别进行回归分析， 并对比其回归函数图像，发现任务未完成的主要原因是用户 没考虑自身限额对定价的影响，其余两个因素相对次要。 问题二中，我们建立了多目标优化模型，其中目标函数为总定价和成功率。 对问题一中的完成与未完成的任务，我们可以分别拟合出其定价曲面，位于这两 个曲面之间的区间即为合理定价区间。除了问题一中三个因素外，任务成功率还 受到周围用户的信誉、预订任务时间等变量的影响。根据已有的数据回归分析， 得到成功率的综合评价函数。 基于合理定价区间的约束，我们分别对定价最优方 案与成功率最优方案进行求解，经过我们的算法优化之后，与原方案相比，我们 可以在同样的平均成功率的前提下将定价总额降低 2.9%；我们也可以用同样的 定价总额将平均成功率提高 9.4%。 问题三中，我们建立基于改进的 DBSCAN 算法的打包方案。确定打包的核 心目的是改善预期成功率较小任务的执行情况。 我们引入了任务的得分半径和用 户得分半径两个参数对原算法中的固定半径进行改进。任务的预期成功率越小， 任务得分半径越大， 用户的信誉度越高、 预订任务时间越早， 用户得分半径越大。 打包后我们还基于用户得分半径检验打包是否合理， 即是否有用户能够执行该任 务。基于该算法，我们一共求得 62 个需要被打包的任务点，被打包成 25 组。将 预期成功率与原成功率进行对比， 成功率最高提升了 7.2%， 平均成功率提升 2.3%， 验证了任务联合打包对于平均成功率的提升有很大作用。 在确定新的定价模型时， 我们将定价划分为两大因素： 任务本身价值与路途花费。根据原数据对这两个因 素的系数进行求解， 我们基于该定价函数对定价进行修改， 得到了新的定价方案。 问题四中，我们根据优化模型以及打包算法对新数据进行定价、打包、成功 率计算， 并得到优化的定价和打包方案并得到相应的优化方案成功率。为了检验 模型的可靠性，我们建立了仿真模拟模型，对每个用户行为进行仿真，结果显示 模拟成功率与优化方案成功率偏差在 20%以内。 最后我们对模型的鲁棒性和灵敏度进行了检验， 发现模型具有较好的鲁棒性。