2018届中考数学复习第一部分数与代数第十二课时一次函数练习_80
(完整word版)2018中考一次函数真题(可编辑修改word版)

一次函数参考答案与试题解析一.选择题(共10 小题)1.(2018•常德)若一次函数y=(k﹣2)x+1 的函数值y 随x 的增大而增大,则()A.k<2 B.k>2 C.k>0D.k<0【分析】根据一次函数的性质,可得答案.【解答】解:由题意,得k﹣2>0,解得k>2,故选:B.2.(2018•台湾)已知坐标平面上,一次函数y=3x+a 的图形通过点(0,﹣4),其中a 为一数,求a 的值为何?()A.﹣12 B.﹣4 C.4 D.12【分析】利用待定系数法即可解决问题.【解答】解:∵次函数y=3x+a 的图形通过点(0,﹣4),∴﹣4=0×3+a,∴a=﹣4,故选:B.3.(2018•娄底)将直线y=2x﹣3 向右平移2 个单位,再向上平移3 个单位后,所得的直线的表达式为()A.y=2x﹣4 B.y=2x+4 C.y=2x+2 D.y=2x﹣2【分析】根据平移的性质“左加右减,上加下减”,即可找出平移后的直线解析式,此题得解.【解答】解:y=2(x﹣2)﹣3+3=2x﹣4.化简,得y=2x﹣4,故选:A.4.(2018•枣庄)如图,直线l 是一次函数y=kx+b 的图象,若点A(3,m)在直线l 上,则m 的值是(),解答A .﹣5B .C .D .7【分析】待定系数法求出直线解析式,再将点 A 代入求解可得.【解答】解:将(﹣2,0)、(0,1)代入,得:,∴y= x +1,将点 A (3,m )代入,得:+1=m ,即 m=,故选:C .月份 1 2 3 4成绩(s ) 15.6 15.4 15.2 15( ) (温馨提示;目前 100m 短跑世界记录为 9 秒 58)A .14.8sB .3.8sC .3sD .预测结果不可靠【分析】由表格中的数据可知,每加 1 个月,成绩提高 0.2 秒,所以 y 与 x 之间是一次函数的关系,可设 y=kx +b ,利用已知点的坐标,即可求解.【解答】解:(1)设 y=kx +b 依题意得(1 分),∴y=﹣0.2x +15.8.当 x=5 时,y=﹣0.2×5+15.8=14.8.故选:A .解得:6.(2018•宿迁)在平面直角坐标系中,过点(1,2)作直线l,若直线l 与两坐标轴围成的三角形面积为4,则满足条件的直线l 的条数是()A.5 B.4 C.3 D.2【分析】根据题意可以设出直线l 的函数解析式,然后根据题意即可求得k 的值,从而可以解答本题.【解答】解:设过点(1,2)的直线l 的函数解析式为y=kx+b,2=k+b,得b=2﹣k,∴y=kx+2﹣k,当x=0 时,y=2﹣k,当y=0 时,x=,令=4,解得,k1=﹣2,k2=6﹣4 ,k3=6+4 ,故满足条件的直线l 的条数是3 条,故选:C.7.(2018•泰州)如图,平面直角坐标系xOy 中,点A 的坐标为(9,6),AB⊥y 轴,垂足为B,点P 从原点O 出发向x 轴正方向运动,同时,点Q 从点A 出发向点B 运动,当点Q 到达点B 时,点P、Q 同时停止运动,若点P 与点Q 的速度之比为1:2,则下列说法正确的是()A.线段PQ 始终经过点(2,3)B.线段PQ 始终经过点(3,2)C.线段PQ 始终经过点(2,2)D.线段PQ 不可能始终经过某一定点【分析】当OP=t 时,点P 的坐标为(t,0),点Q 的坐标为(9﹣2t,6).设直线PQ 的解析式为y=kx+b(k≠0),利用待定系数法求出PQ 的解析式即可判断;【解答】解:当OP=t 时,点P 的坐标为(t,0),点Q 的坐标为(9﹣2t,6).设直线PQ 的解析式为y=kx+b(k≠0),将P(t,0)、Q(9﹣2t,6)代入y=kx+b,,解得:,∴直线PQ 的解析式为y=x+ .∵x=3 时,y=2,∴直线PQ 始终经过(3,2),故选:B.8.(2018•湘潭)若b>0,则一次函数y=﹣x+b 的图象大致是()A.B.C.D.【分析】根据一次函数的k、b 的符号确定其经过的象限即可确定答案.【解答】解:∵一次函数y=x+b 中k=﹣1<0,b>0,∴一次函数的图象经过一、二、四象限,故选:C.9.(2018•南充)直线y=2x 向下平移2 个单位长度得到的直线是()A.y=2(x+2)B.y=2(x﹣2)C.y=2x﹣2 D.y=2x+2【分析】据一次函数图象与几何变换得到直线y=2x 向下平移 2 个单位得到的函数解析式为y=2x﹣2.【解答】解:直线y=2x 向下平移 2 个单位得到的函数解析式为y=2x﹣2.故选:C.10.(2018•南通)函数y=﹣x 的图象与函数y=x+1 的图象的交点在()A.第一象限B.第二象限C.第三象限D.第四象限【分析】根据题目中的函数解析式可以求得这两个函数的交点坐标,从而可以解答本题.【解答】解:,解得,,∴函数y=﹣x 的图象与函数y=x+1 的图象的交点是(,),故函数y=﹣x 的图象与函数y=x+1 的图象的交点在第二象限,故选:B.。
2018年全国一次函数中考题(含答案)

3. (2018年山东省枣庄市,5,3分) 如图,直线l 是一次函数b kx y +=的图象,如果点),3(m A 在直线l 上,则m 的值为( )A .5-B .23C .25D .7 【答案】C【解析】由图像可得直线l 与x 轴的两个交点的坐标为(0,1)(-2,0),代入到b kx y +=求得直线 l 的解析式为112y x =+,再把点),3(m A 代入到直线l 的解析式中,求得m 的值为25.故选C. 【知识点】点的坐标;待定系数法求一次函数的表达式;4. (2018四川省南充市,第7题,3分)直线2y x =向下平移2个单位长度得到的直线是( )A .2(2)y x =+B .2(2)y x =-C .22y x =-D .22y x =+ 【答案】C【解析】直线y =2x 向下平移2个单位长度得到直线的解析式是y =2x -2,故选C. 【知识点】一次函数的平移5. (2018浙江绍兴,6,3分)如图,一个函数的图象由射线BA 、线段BC 、射线CD 组成,其中点(1,2)A -,(1,3)B ,(2,1)C ,(6,5)D ,则此函数( )(第6题图)A .当1x <时,y 随x 的增大而增大B .当1x <时,y 随x 的增大而减小C .当1x >时,y 随x 的增大而增大D .当1x >时,y 随x 的增大而减小【答案】A【解析】由函数图像可知,当1x <时,y 随x 的增大而增大,A 正确;当x 1<<2时,y 随x 的增大而减小,B 错误;当2x >时,y 随x 的增大而增大,C 错误,当1x >时,y 随x 的增大而增大,D 错误,故选A 。
【知识点】一次函数的性质 1. (2018贵州遵义,7题,3分)如图,直线y=kx+3经过点(2,0),则关于x 的不等式kx+3>0的解集是A.x>2B.x<2C.x≥2D.x≤2【答案】B【解析】由图可知,函数y=kx+3随着x 的增大而减小,与x 轴的交点为(2,0),kx+3>0,即y>0,即图像在x 轴上方的部分,故不等式的解集为x<2 【知识点】一次函数与一元一次不等式的关系,数形结合3. (2018湖南省湘潭市,7,3分)若b >0,则一次函数y=-x+b 的图象大致是( )【答案】C【解析】根据一次函数y=kx+b 中,k >0时,图象从左到右上升;k <0时,图象从左到右下降;b >0时,图象与y 轴的交点在y 轴上方;b=0时,图象与y 轴的交点在原点;b <0时,图象与y 轴的交点在y 轴下方.∵-1<0,所以图象从左到右下降,b >0所以图象与y 轴交于y 轴上方,故选择C.【知识点】一次函数的图象和性质4. (2018山东德州,10,3分)给出下列函数:①32y x =-+;②3y x=;③22y x =;④3y x =.上述函数中符合条件“当1x >时,函数值y 随自变量x 增大而增大”的是( ) A .①③ B .③④ C.②④ D .②③ 【答案】B【解析】函数32y x =-+的y 随自变量x 增大而减小;因为函数3y x=在每个象限内时的y 随自变量x 增大而减小,所以在当1x >时的y 随自变量x 增大而减小;函数22y x =在0x >时的y 随自变量x 增大而增大,所以在当1x >时的y 随自变量x 增大而增大;函数3y x =的y 随自变量x 增大而增大. 故选B.【知识点】函数增减性5. (2018广东省深圳市,7,3分)把函数y =x 向上平移3个单位,下列在该平移后的直线上的点是( ) A .(2,2) B .(2,3) C .(2,4) D .(2,5) 【答案】D【解析】一次函数的平移规律是:左加右减,上加下减,故把函数y =x 向上平移3个单位后的函数关系式为y =x +3,当x =2时,y =2+3=5,故选D . 【知识点】一次函数的平移;点的坐标6.(2018湖北荆州,T7,F3)已知:将直线1y x =-向上平移2个单位长度后得到直线y kx b =+,则下列关于直线y kx b =+的说法正确的是( )A.经过第一、二、四象限B.与x 轴交于(1,0)C.与y 轴交于(0,1)D.y 随x 的增大而减小 【答案】C【解析】解:根据题意,将直线y=x ﹣1向上平移2个单位后得到的直线解析式为:y=x-1+2,即y=x +1,当x=0时,y=1, ∴与y 轴交于点(0,1);当y=0时,x=-1,与x轴交于点(-1,0);图象经过第一、二、三象限;y 随x 的增大而增大.故选B . 【知识点】一次函数图象的平移、坐标轴的交点、函数值随自变量的增减情况.7. (2018广西玉林,5题,3分)等腰三角形底角与顶角之间的函数关系是 A.正比例函数 B.一次函数 C.反比例函数 D.二次函数 【答案】B【解析】设顶角为x ,底角为y ,由三角形内角和定理可得,y=12(180-x)=-12x+90,所以二者之间为一次函数关系,故选B【知识点】三角形内角和,一次函数8. (2018陕西,4,3分)如图,在矩形ABCD 中,A (-2,0),B (0,1). 若正比例函数y =kx 的图象经过点C ,则k 的值为( ) A .12-B .12C .-2D .2【答案】A【解析】由A(-2,0),B(0,1)可得C(-2,1).把点C代入y=kx,得:-2k=1,1 2k=-,故选择A.【知识点】正比例函数,图形与坐标9.(2018陕西,7,3分)若直线l1经过点(0,4),l2经过点(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为()A.(-2,0)B.(2,0)C.(-6,0)D.(6,0)【答案】B【解析】设直线l1解析式为y1=kx+4,∵l1与l2关于x轴对称,∴直线l2的解析式为y2=-kx-4,∵l2经过点(3,2),∴-3k-4=2.∴k=-2.∴两条直线的解析式分别为y1=-2x+4,y2=2x-4联立方程组,解得:x=2,y=0.∴交点坐标为(2,0),故选择B.【知识点】一次函数2.(2018浙江衢州,第14题,4分)星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是________千米。
2018年 九年级数学中考复习 一次函数 专题训练题 含答案

2018年九年级数学中考复习一次函数专题训练题含答案则m的值为( )A.2 B.-2 C.4 D.-49. 正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )10. 已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的表达式为( )A.y=-x-2 B.y=-x-6 C.y=-x+10 D.y=-x-111. 为了增强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元,超过10吨时,超过的部分按每吨1.8元收费.该市某户居民5月份用水x吨(x>10),应交水费y元,则y关于x的函数关系式是__ __.12. 将直线y=2x+1平移后经过点(2,1),则平移后的直线关系式为__ .13. 若一次函数y=-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是__ __.(写出一个即可)14. 根据下表中一次函数的自变量x与函数y的对应值,可得p的值为____.x-2 0 1 …y 3 p0 …15. 写出下列各题中y关于x的函数关系式,并判断y是否为x的一次函数,是否为正比例函数.(1)长方形的面积为20,长方形的长y与宽x之间的关系;(2)刚上市时西瓜每千克3.6元,买西瓜的总价y元与所买西瓜x千克之间的关系;(3)仓库内有粉笔400盒,如果每个星期领出36盒,仓库内余下的粉笔盒数y 与星期数x 之间的关系.16. 已知一次函数y =(k -2)x +3k 2-12.(1) k 为何值时,图象平行于y =-2x 的图象?(2) k 为何值时,图象经过原点?参考答案:1---10 BBCDD DCBBC11. y =1.8x -612. y =2x -313. -114. 115. (1)y =20x,不是一次函数,也不是正比例函数 (2)y =3.6x ,是一次函数,也是正比例函数(3)y =-36x +400,是一次函数,不是正比例函数16. (1)∵一次函数的图象平行于y =-2x 的图象,∴k-2=-2,∴k=0(2)∵一次函数y =(k -2)x +3k 2-12的图象经过原点,∴⎩⎪⎨⎪⎧3k 2-12=0,k -2≠0,解得k =-2。
2018年中考总复习之一次函数及反比例函数题的经典题型汇总(含答案)

面积,S2 为△OAB的面积,若 = ,则b的值是
.
解:(1)设点 P 的坐标为(m,n),则点 Q 的坐标为(m﹣1,n+2),
依题意得:
,解得:k=﹣2.故答案 为:﹣2.
(2)∵BO⊥x 轴,CE⊥x 轴,∴BO∥CE,∴△AOB∽△AEC.
∵点 M 是一次函数 Y=2x-4 与 Y 轴的交点,∴点 M 的坐标为(0,-4) 设 C 点的坐标为(0,Yc),由题意知
点的坐标为0yc由题意知3yc41yc410解得yc4当yc40时yc45解得yc1当yc40时yc45解得yc9的坐标为01或0922已知点p在一次函数ykxbkb向左平移1个单位再向上平移2个单位得到点q点q也在该函数ykxb2如图该一次函数的图象分别与x轴y轴交于ab两点且与反比例函数y图象交于cd两点点c在第二为四边形ceob的面积s2box轴cex轴boceaobaec
并求
的面积。
(2)若反比例函数 y= (x>0)的图象经过点 M, 求该反比函数的解析式,并通过计算判断点 N 是否在该函数的图象上.
1、如图,在平面直角坐标系 xoy 中,反比例函数 y = 的图象与一次函数 y =k(x -2 )
的图象交点为 A(3,2),B(x,y)。 (1)求反比例函数与一次函数的解析式及 B 点坐标; (2)若 C 是 y 轴上的点,且满足△ABC 的面积为 10, 求 C 点坐标。
3、如图,直线 y=x+4 与双曲线 y= (k≠0)相交于 A(﹣1,a)、B 两点,在 y
轴上找一点 P,当 PA+PB 的值最小时,点 P 的坐标为?
(1)k的值是
;
4、如图,在直角坐标系中,直线 y=﹣ x 与反比例函数 y= 的图象交于关于原点对
2018届中考数学复习第一部分数与代数第十二课时一次函数练习_80

第12课时一次函数备考演练一、精心选一选1.(2015·陕西)设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m=( A )A.2B.-2C.4D.-42.( 2016·邵阳)一次函数y=-x+2的图象不经过的象限是(C )A.第一象限B.第二象限C.第三象限D.第四象限3.(2016·广州)若一次函数y=ax+b的图象经过第一、二、四象限,则下列不等式中总是成立的是( C )A.b<0B.a-b>0C.a2+b>0D.a+b>04.(2015·辽阳)如图,直线y=-x+2与y=ax+b(a≠0且a,b为常数)的交点坐标为(3,-1),则关于x的不等式-x+2≥ax+b的解集为( D ) A.x≥-1 B.x≥3C.x≤-1D.x≤3二、细心填一填5.(2015·无锡)一次函数y=2x-6的图象与x轴的交点坐标为(3,0).6.(2016·娄底)将直线y=2x+1向下平移3个单位长度后所得直线的解析式是y=2x-2.7.(2015·永州)已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x≥2时,y≤0.三、用心解一解8.(2014·怀化)设一次函数y=kx+b(k≠0)的图象经过A(1,3)、B(0,-2)两点,试求k,b的值.解:把A(1,3)、B(0,-2)代入y=kx+b得,解得,即k,b的值分别为5,-2.9.(2013·陕西)“五一节”期间,申老师一家自架游去了离家170千米的某地.下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.(1)求他们出发半小时时,离家多少千米?(2)求出AB段图象的函数表达式;(3)他们出发2小时时,离目的地还有多少千米?解:(1)设函数的解析式为y=ax,由图象可知该函数的图象过点(1. 5,90),y=60x,当x=0.5,y=30;(2)设函数的解析式为y=kx+b,由图象可知过点(1.5,90)和(2.5,170)∴函数关系式为y=80x-30;(3)令x=2,∴y=130,∴他们出发2小时时,离目的地还有40千米.。
河北省2018年中考数学总复习一次函数专题(无答案).doc
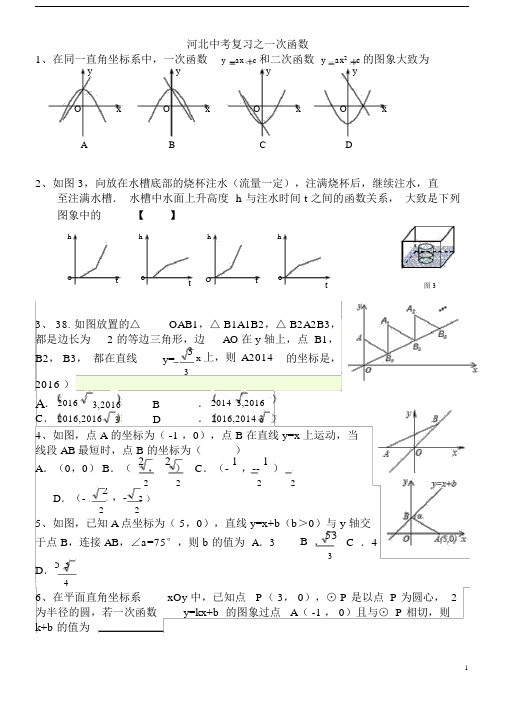
河北中考复习之一次函数1、在同一直角坐标系中,一次函数 y ax c 和二次函数y ax 2 c 的图象大致为y y y yO x O x O x O xA B C D2、如图 3,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽. 水槽中水面上升高度 h 与注水时间 t 之间的函数关系, 大致是下列图象中的 【 】hhhhOtOtOtOt图 33、 38. 如图放置的△ OAB1,△ B1A1B2,△ B2A2B3, 都是边长为 2 的等边三角形,边 AO 在 y 轴上,点 B1,B2, B3, 都在直线 y= 3x 上,则 A2014 的坐标是,2016 )3A . 20163,2016B . 2014 3,2016C . 2016,2016 3D . 2016,2014 34、如图,点 A 的坐标为( -1 ,0),点 B 在直线 y=x 上运动,当 线段 AB 最短时,点 B 的坐标为( )A .(0,0)B .( 2 , 2 )C .(- 1 ,-- 1)2 222D .(-2,-2 )225、如图,已知 A 点坐标为( 5,0),直线 y=x+b (b >0)与 y 轴交于点 B ,连接 AB ,∠a=75°,则 b 的值为 A .3 B .53 C .43D .5 346、在平面直角坐标系 xOy 中,已知点 P ( 3, 0),⊙ P 是以点 P 为圆心, 2为半径的圆,若一次函数y=kx+b 的图象过点 A ( -1 , 0)且与⊙ P 相切,则 k+b 的值为7、某工厂现有甲种原料 360 千克,乙种原料290 千克,计划用这两种原料生产A、B两种产品,共 50 件,已知生产一件 A 产品,需用甲种原料 9 千克、乙种原料 3 千克,可获利润 700 元,已知生产一件 B产品,需用甲种原料 4 千克、乙种原料 10 千克,可获利润 1200 元,(1)按要求安排 A、B 两种产品的生产件数,有哪几种方案?请你给设计出来.(2)设生产 A 、B 两种产品获总利润为 y(元),其中一种的生产件数为 x,试写出 y 与 x 之间的函数关系式,并利用函数的性质说明( 1)中哪种生产方案获总利润最大?最大利润是多少?8、某工厂有甲、乙两条生产线先后投产,在乙生产线投产y(吨) 600以前,甲生产线已生产了 200 吨成品;从乙生产线投产开400始,甲、乙两条生产线每天分别生产 20 吨和 30 吨成品。
一次函数单元练习题精选(2018中考题)
解:(1)将点 A(6,0)代入直线 AB 的表达式可得 0=-6-b,解得 b=-6, ∴ 直线 AB 的表达式为 y=-x+6, ∴ B 点坐标为(0,6). (2)∵ OB∶OC=3∶1,∴ OC=2, ∴ 点 C 的坐标为(-2,0), 设 BC 的表达式是 y=kx+6,0=-2k+6,解得 k=3. ∴ 直线 BC 的表达式为 y=3x+6.
)
B.y 值随着 x 的增大而减小 D.当 x>1 时,y>0
3.(2017· 泰安)已知一次函数 y=kx-m-2x 的图象与 y 轴的负半轴相交,且函数值 y 随自变量 x 的增大而减小,则下列结论正确的是( A.k<2,m>0 B.k<2,m<0 C.k>2,m>0 ) D.k<0,m<0
考点 2
1 y=- x+60. 10
11. (2018· 临沂)甲、乙两人分别从 A,B 两地同时出发,匀速相向而行.甲的速度大 于乙的速度,甲到达 B 地后,乙继续前行.设出发 x h 后,两人相距 y km,图中折 线表示从两人出发至乙到达 A 地的过程中 y 与 x 之间的函数关系. 根据图中信息,求: (1)点 Q 的坐标,并说明它的实际意义; (2)甲、乙两人的速度.
解:(1)设直线 PQ 的表达式为 y=kx+b,
1 15 代入点(0,10)和4, 2 的坐标,
1 15 4k+b= 2 , 得 b=10,
k=-10, 解得 b=10.
故直线 PQ 的表达式为 y=-10x+10. 当 y=0 时,x=1,故点 Q 的坐标为(1,0),该点表示甲、乙两人经过 1 小时相遇.
变式 4.已知函数 y=kx+b(k≠0)的图象与 y 轴交点的纵坐标为-2,且当 x=2 时,y= 1.那么此函数的表达式为________. 5.如图,直线 AB:y=-x-b 分别与 x、y 轴交于 A(6,0),B 两点,过点 B 的直线 交 x 轴的负半轴于点 C,且 OB∶OC=3∶1. (1)求点 B 的坐标; (2)求直线 BC 的函数关系式; (3)若点 P(m,2)在△ABC 的内部,求 m 的取值范围.
2018年中考数学精选题专练一次函数(含答案)
20. 在一条笔直的公路上有 A.B 两地,甲骑自行车从 A 地到 B 地;乙骑自行车从 B 地到 A 地,
到达 A 地后立即按原路返回,如图是甲、乙两人距
B 地的距离 y(km)与行驶时间 x( h)之间
的函数图象,根据图象解答以下问题:
( 1)写出 A. B 两地之间的距离;
( 2)求出点 M的坐标,并解释该点坐标所表示的实际意义;
将 C(3, 2)代入 y=kx ,得 2=3k,∴ k= ;故答案为: ;
( 2)k 的值不会发生变化,理由:∵正方形边长为
a,∴ AB=a,
在直线 y=2x 中,当 y=a 时, x= ,∴ OA= , OD= ,∴ C( , a),
将 C( , a)代入 y=kx ,得 a=k× ,∴ k= .
路径 A→ D→C→ E运动,则△ APE的面积 y与点 P经过的路径长 x之间的函数关系用图象表示大致是 ()
二、填空题 :
9. 若将一次函数 y=﹣2x+1 的图象向
(上或下)平移
单位,使平移后的图象过点
( 0, ﹣ 2).
10. 已知直线 y=( k+2) x+
的截距为 1,那么该直线与 x 轴的交点坐标为
别表示行驶距离和时间,则这两人骑自行车的速度相差
km/ h.
s,t 分
15. 如图,在平面直角坐标系中,已知点 A(0, 4), B(﹣ 3, 0)轴上的点 A′处,折痕所在的直线交 y 轴正半轴于点 C,则点 C的坐
标为
.
16. 如图是某汽车行驶的路程 s( km)与时间 t ( m/n)的函数关系图,观察图中所提供的信息,
解答下列问题:
( 1)汽车在前 9 分钟内的平均速度是
2018年全国有关中考数学试题分类汇编(一次函数)(K12教育文档)
2018年全国有关中考数学试题分类汇编(一次函数)(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018年全国有关中考数学试题分类汇编(一次函数)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018年全国有关中考数学试题分类汇编(一次函数)(word版可编辑修改)的全部内容。
2018年全国有关中考数学试题分类汇编(一次函数)一、选择题1所示,那1、(2007福建福州)已知一次函数(1)y a x b =-+的图象如图么a 的取值范围是( )A A .1a >B .1a <C .0a >D .0a <2、(2007上海市)如果一次函数y kx b =+的图象经过第一象限,且与y 轴负半轴相交,那么( )B A .0k >,0b >B .0k >,0b <C .0k <,0b >D .0k <,0b <3、(2007陕西)如图2,一次函数图象经过点A ,且与正比例函数y x =-的图象交于点B ,则该一次函数的表达式为( )B A .2y x =-+ B .2y x =+C .2y x =-D .2y x =--4、(2007浙江湖州)将直线y =2x 向右平移2个单位所得的直线的解析式是( )。
CA 、y =2x +2B 、y =2x -2C 、y =2(x -2)D 、y =2(x +2)5、(2007浙江宁波)如图,是一次函数y=kx+b 与反比例函数y=2x的图像,则关于x 的方程kx+b=2x的解为( )C(A )x l =1,x 2=2 (B )x l =—2,x 2=-1 (C )x l =1,x 2=—2 (D)x l =2,x 2=-16、(2007四川乐山)已知一次函数y kx b =+的图象如图(6)所示,当1x <时,y 的取值范围是( )C A.20y -<<B.40y -<<C.2y <-D.4y <-7、(2007浙江金华)一次函数1y kx b =+与2y x a =+的图象如图,则下列结论①0k <;②0a >;③当3x <时,12y y <中,正确的个数是( )B图1Oxy图(6)0 2 -4xyOxy AB1- y x =- 2图2A .0B .1C .2D .3二、填空题1、(2007福建晋江)若正比例函数kx y =(k ≠0)经过点(1-,2),则该正比例函数的解析式为=y ___________。
2018年中考数学总复习一次函数专题复习练习及答案
2018 初三中考数学复习一次函数专题复习练习1. 下列表达式中,y不是x的函数的是( B )A.y=-x2 B.y2=x C.y=|x| D.y=-x2+12.下列函数中,自变量x的取值范围是x>0的函数是( D )A.y=x B.y=1xC.y=x2+1 D.y=12x-13. 下列变量之间的变化关系不是一次函数的是( B )A.圆的周长和它的半径 B.圆的面积和它的半径C.2x+y=5中的y和x D.正方形的周长C和它的边长a4.下列说法中不正确的是( D )A.一次函数不一定是正比例函数B.不是一次函数就一定不是正比例函数C.正比例函数是特殊的一次函数D.不是正比例函数就一定不是一次函数5. 下列图象中,表示y是x的函数的个数有( B )A.1个 B.2个 C.3个 D.4个6.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长恰好为24米,要围的菜园是如图所示的矩形ABCD,设BC的边长为x米,AB边的长为y米,则y与x之间的函数关系式是( B )A .y =-2x +24(0<x<12)B .y =-12x +12(0<x<24)C .y =2x -24(0<x<12)D .y =12x -12(0<x<24)7.一次函数y =mx +|m -1|的图象过点(0,2),且y 随x 的增大而增大,则m 等于( B )A .-1B .3C .1D .-1或38.下列四组点中可以在同一个正比例函数图象上的一组点是( A ) A .(2,-3),(-4,6) B .(-2,3),(4,6) C .(-2,-3),(4,-6) D .(2,3),(-4,6) 9.对于函数y =-12x +3,下列说法错误的是( C )A .图象经过点(2,2)B .y 随着x 的增大而减小C .图象与y 轴的交点是(6,0)D .图象与坐标轴围成的三角形面积是9 10.关于x 的一次函数y =kx +k 2+1的图象可能正确的是( C )11.P 1(x 1,y 1),P 2(x 2,y 2)是一次函数y =-2x +5图象上的两点,且x 1<x 2,则y 1与y 2的大小关系是( C )A .y 1<y 2B .y 1=y 2C .y 1>y 2D .y 1>y 2>012.已知一次函数y =32x +m 和y =-12x +n 的图象都经过点A(-2,0),且与y 轴分别交于B ,C 两点,那么△ABC 的面积是( C ) A .2 B .3 C .4 D .613.如图,把Rt △ABC 放在直角坐标系内,其中∠CAB =90°,BC =5,点A ,B 的坐标分别为(1,0),(4,0),将△ABC 沿x 轴向右平移,当点C 落在直线y =2x -6上时,线段BC 扫过的面积为( C )A .4B .8C .16D .8 214.如图,已知直线l ∶y =33x ,过点A(0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;…;按此作法继续下去,则点A 2 013的坐标为( C )A .(0,22 013)B .(0,22 014)C .(0,24 026)D .(0,24 024) 15.将直线y =2x 向上平移1个单位长度后得到的直线是__y =2x +1__. 16.函数y =x +3x -4中,自变量x 的取值范围是__x ≥0且x ≠4__.17.一次函数y =(m +2)x +1,若y 随x 的增大而增大,则m 的取值范围是 __m >-2__.18.直线y =3x -m -4经过点A(m ,0),则关于x 的方程3x -m -4=0的解是 __x =2__.19.已知某一次函数的图象经过点A(0,2),B(1,3),C(a ,1)三点,则a 的值是__-1__.20.某农场租用播种机播种小麦,在甲播种机播种2天后,又调来乙播种机参与播种,直至完成800亩的播种任务.播种亩数与天数之间的函数关系如图,那么乙播种机参与播种的天数是__4__.21.经过点(2,0)且与坐标轴围成的三角形面积为2的直线解析式为__y =x -2或y =-x +2__.22.直线l 与y =-2x +1平行,与直线y =-x +2交点的纵坐标为1,则直线l 的解析式为__y =-2x +3__.23.已知:一次函数y =kx +b 的图象经过M(0,2),N(1,3)两点. (1)求k ,b 的值;(2)若一次函数y =kx +b 的图象与x 轴的交点为A(a ,0),求a 的值.解:(1)由条件得b =2,把⎩⎪⎨⎪⎧x =1y =3代入y =kx +2中得k =1(2)由(1)得y =x +2,当y =0时,x =-2,即a =-224.联通公司手机话费收费有A 套餐(月租费15元,通话费每分钟0.1元)和B 套餐(月租费0元,通话费每分钟0.15元)两种.设A 套餐每月话费为y 1(元),B 套餐为y 2(元),月通话时间为x 分钟.(1)分别表示出y 1与x ,y 2与x 的函数关系式; (2)月通话时间多长时,A ,B 两种套餐收费一样? (3)什么情况下A 套餐更省钱? 解:(1)y 1=0.1x +15,y 2=0.15x(2)由y 1=y 2得0.1x +15=0.15x 解得x =300 (3)当通话时间多于300分钟时,A 套餐省钱25.设函数y =x +n 的图象与y 轴交于点A ,函数y =-3x -m 的图象与y 轴交于点B ,两个函数的图象交于点C(-3,1),D 为AB 中点. (1)求m ,n 的值;(2)求直线DC 的一次函数表达式. 解:(1)m =8,n =4(2)由(1)得A(0,4),B(0,-8).因为D 是AB 的中点,所以D(0,-2),设直线CD 的表达式为y =kx +b ;⎩⎪⎨⎪⎧b =-2,-3k +b =1解得⎩⎪⎨⎪⎧k =-1b =-2,即y =-x -226.某生物小组观察一植物生长,得到植物的高度(单位:厘米)与观察时间(单位:天)的关系,并画出如下的图象(AC 是线段,直线CD 平行于x 轴.) (1)该植物从观察时起,多少天以后停止长高? (2)求直线AC 的表达式,并求该植物最高长多少厘米?解:(1)50天后(2)设直线AC 的表达式为y =kx +6,将(30,12)代入,得12=30k +6,解得k =15,表达式为y =15x +6,最高长16厘米27.1号探测气球从海拔5 m 处出发,以1 m/min 的速度上升.与此同时,2号探测气球从海拔15 m 处出发,以0.5 m/min 的速度上升,两个气球都匀速上升了50min.设气球上升时间为 x min(0≤x ≤50) (1)根据题意,填写下表:(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由;(3)当30≤x ≤50时,两个气球所在位置的海拨最多相差多少米? 解:(1)35 x +5 20 0.5x +15(2)能.由x +5=0.5x +15得x =20,所以x +5=25,即气球上升20 min 时位于海拔25 m 处(3)当30≤x ≤50时,1号气球始终在2号汽球上方,设两气球的海拔差为y ,则y =(x +5)-(0.5x +15)=0.5x -10,y 随x 的增大而增大,所以当x =50时,y 的值最大,为15米28.如图,直线y =kx +6与x 轴、y 轴分别相交于点E ,F ,点E 的坐标为(-8,0),点A 的坐标为(-6,0),点P(x ,y)是第二象限内的直线上的一个动点. (1)求k 的值;(2)在点P 的运动过程中,写出△OPA 的面积S 与x 的函数表达式,并写出自变量x 的取值范围;(3)探究:当P 运动到什么位置(求P 的坐标)时,△OPA 的面积为278?解:(1)k =34(2)由(1)得y =34x +6所以S =12×6×(34x +6)所以S =94x +18(-8<x<0)(3)由S =94x +18=278得x =-132,y =34×(-132)+6=98,所以P(-132,98)即P 运动到点(-132,98)时,△OPA 的面积为27829.阅读下面的材料:在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y =k 1x +b 1(k 1≠0)的图象为直线l 1,一次函数y =k 2x +b 2(k 2≠0)的图象为直线l 2,若k 1=k 2,且b 1≠b 2,我们就称直线l 1与直线l 2互相平行.解答下面的问题:(1)求过点P(1,4)且与已知直线y =-2x -1平行的直线l 的函数表达式,并画出直线l 的图象;(2)设直线l 分别与y 轴、x 轴交于点A ,B ,如果直线m :y =kx +t(t >0)与直线l 平行且交x 轴于点C ,求出△ABC 的面积S 关于t 的函数表达式.解:(1)y =-2x +6,图略(2)当0<t<6时,S =9-32t ;当t ≥6时,S =32t -9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12课时一次函数
备考演练
一、精心选一选
1.(2015·陕西)设正比例函数y=mx的图象经过点A(m,4),且y的值随
x值的增大而减小,则m=( A )
A.2
B.-2
C.4
D.-4
2.( 2016·邵阳)一次函数y=-x+2的图象不经过的象限是(C )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.(2016·广州)若一次函数y=ax+b的图象经过第一、二、四象限,
则下列不等式中总是成立的是( C )
A.b<0
B.a-b>0
C.a2+b>0
D.a+b>0
4.(2015·辽阳)如图,直线y=-x+2与y=ax+b(a≠0且a,b为常数)的交
点坐标为(3,-1),则关于x的不等式-x+2≥ax+b的解集为( D )
A.x≥-1
B.x≥3
C.x≤-1
D.x≤3
二、细心填一填
5.(2015·无锡)一次函数y=2x-6的图象与x轴的交点坐标为
(3,0).
6.(2016·娄底)将直线y=2x+1向下平移3个单位长度后所得直线的
解析式是y=2x-2.
7.(2015·永州)已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),
则当x≥2时,y≤0.
三、用心解一解
8.(2014·怀化)设一次函数y=kx+b(k≠0)的图象经过A(1,3)、B(0,-2)两点,试求k,b的值.
解:把A(1,3)、B(0,-2)代入y=kx+b
得,解得,
即k,b的值分别为5,-2.
9.(2013·陕西)“五一节”期间,申老师一家自架游去了离家170千米的某地.下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求他们出发半小时时,离家多少千米?
(2)求出AB段图象的函数表达式;
(3)他们出发2小时时,离目的地还有多少千米?
解:(1)设函数的解析式为y=ax,由图象可知该函数的图象过点(1. 5,90),y=60x,当x=0.5,y=30;
(2)设函数的解析式为y=kx+b,由图象可知过点(1.5,90)和(2.5,170)
∴函数关系式为y=80x-30;
(3)令x=2,∴y=130,
∴他们出发2小时时,离目的地还有40千米.。
