基于EViews的我国农产品产量与相关投入的模型分析与预测检验
eviews实验指导(ARIMA模型建模与预测)
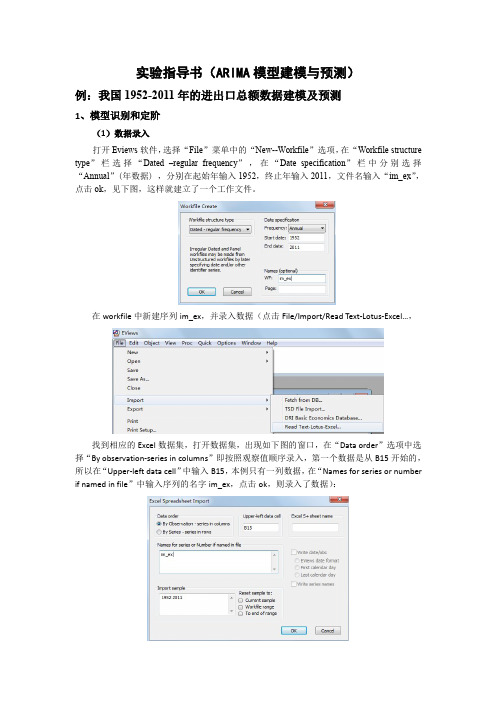
实验指导书(ARIMA模型建模与预测)例:我国1952-2011年的进出口总额数据建模及预测1、模型识别和定阶(1)数据录入打开Eviews软件,选择“File”菜单中的“New--Workfile”选项,在“Workfile structure type”栏选择“Dated–regular frequency”,在“Date specification”栏中分别选择“Annual”(年数据),分别在起始年输入1952,终止年输入2011,文件名输入“im_ex”,点击ok,见下图,这样就建立了一个工作文件。
在workfile中新建序列im_ex,并录入数据(点击File/Import/Read Text-Lotus-Excel…,找到相应的Excel数据集,打开数据集,出现如下图的窗口,在“Data order”选项中选择“By observation-series in columns”即按照观察值顺序录入,第一个数据是从B15开始的,所以在“Upper-left data cell”中输入B15,本例只有一列数据,在“Names for series or number if named in file”中输入序列的名字im_ex,点击ok,则录入了数据):(2)时序图判断平稳性双击序列im_ex ,点击view/Graph/line,得到下列对话框:得到如下该序列的时序图,由图形可以看出该序列呈指数上升趋势,直观来看显著非平稳。
40,00080,000120,000160,000200,000240,000556065707580859095000510IM_EX(3)原始数据的对数处理因为数据有指数上升趋势,为了减小波动,对其对数化,在Eviews 命令框中输入相应的命令“series y=log(im_ex)”就得到对数序列,其时序图见下图,对数化后的序列远没有原始序列波动剧烈:45678910111213556065707580859095000510Y从图上仍然直观看出序列不平稳,进一步考察序列y 的自相关图和偏自相关图:从自相关系数可以看出,呈周期衰减到零的速度非常缓慢,所以断定y 序列非平稳。
应用eviews分析数据和预测

统计预测与决策论文摘要:随着市场经济的多元化发展。
统计软件被广泛的应用,企业应用统计软件进行对下一期的生产值进行预测。
从而能更准确的做出决策。
本文利用eviews对某企业的下几期的生产值进行预测,便于企业做出最准确的决策。
关键字:平稳序列,模型识别,模型定阶,模型参数估计,模型检验,模型预测。
下表是某企业近期一百个生产数据值。
1、模型识别绘制序列时序图7680848892255075100125150175200PRODUCTI ON2模型定阶绘制序列相关图从相关图看出,自相关系数迅速衰减为0,说明序列平稳,但最后一列白噪声检验的Q 统计量和相应的伴随概率表明序列存在相关性,因此序列为平稳非白噪声序列。
模型定阶:由图2-5看出,偏自相关系数在k=3后很快趋于0即3阶截尾,尝试拟合AR (3);自相关系数在k=1处显著不为0,当k=2时在2倍标准差的置信带边缘,可以考虑拟合MA (1)或MA (2);同时可以考虑ARMA (3,1)模型等。
原序列做描述统计分析见图481216207880828486889092Series: PRODUCTION Sample 1 201Observations 201Mean 84.11940Median 84.10000Maximum 91.70000Minimum 76.50000Std. Dev. 2.906625Skewness 0.107191Kurtosis 2.752406Jarque-Bera 0.898321Probability0.638164可见序列均值非0,我们通常对0均值平稳序列做建模分析,所以需要在原序列基础上生成一个新的0均值序列。
这个序列是0均值的平稳非白噪声序列,新序列的描述统计量见图 048121620-8-6-4-22468Series: XSample 1 201Observations 201Mean 2.99e-06Median -0.019400Maximum 7.580600Minimum -7.619400Std. Dev. 2.906625Skewness 0.107191Kurtosis 2.752406Jarque-Bera 0.898321Probability0.6381643模型参数估计由伴随概率可知,AR (i )(i=1,2,3)均高度显著,表中最下方给出的是滞后多项式φ-1(x )=0的倒数根,只有这些值都在单位圆内时,过程才平稳。
中国小麦产量简单分析

中国小麦产量简单计量分析尊敬的老师:感谢您抽时间检查我们的作业!我已经尽力自己做了,本科我学的会计,先前没有接触过计量经济学,所以感觉自己学的不是很到位,如果有做得很幼稚的地方,请您不要生气,老师祝您身体健康,笑口常开!假设模型:模型设定为:Y=β0 +β1X1+β2X2+β3X3+β4X4+β5X5+β6X6(Y为小麦产量,X1为小麦播种量,X2为有效灌溉面积,X3为受灾面积,X4为农用复合肥使用量,X5为农药使用量,X6为虚拟变量农业税,取消农业税和有农业税的值分别设为1和0)1、用EVIEWS对建立的模型进行最小二乘法估计得:图1如图1所示,R-squared的值为0.93,F的值为38.45 说明整体的拟合效果较好,但是x2、x3、x5、x6的t检验值并不显著,x2、x5系数的符号不符合经济意义,考虑存在多重共线性。
2、多重共线性检验和修正图2如图2所示,x2与x4、x5的相关系数以及x4和x5的相关系数分别为0.978、0.970和0.996,存在高度相关性。
由于采用逐步回归法得到的单个解释变量的R-squared值都很不理想(见eviews文件),故采用直接去除引起多重共线性的解释变量来对模型修正。
由于x2、x3、x5、x6的参数检验都不显著,而方程的拟合度较高因此直接去掉x2有效灌溉面积、x3受灾面积、x5农药使用量和x6农业税虚拟变量来对模型进行修正。
修正后的回归如图3所示:图3c、x1和x2 的t检验的P值小于0.05,通过检验,整体的F检验对应的P值也小于0.05通过检验,同时符号也符合经济意义。
R-squared的值是0.90,拟合程度高。
最终建立模型Y=β0+β1x1+β4x4.3、自相关检验和修正如图3所示,在模型Y=β0+β1x1+β4x4下利用DW检验方法进行自相关检验的DW值约是2.12,查表得,在n=24,k=3条件下,dl=1.19,du=1.55。
dl<DW<du,即1.19<2.12<2.45,所以DW检验无自相关。
计量经济学论文(eviews分析)-中国食品价格指数的影响因素分析

中国食品价格指数的影响因素分析摘要:本文试从影响食品价格指数的外因粮食价格指数、肉禽及其制品价格指数、水产品价格指数、蔬菜价格指数等进行分析和探讨,并在比较相关线性回归方程后,建立合理的食品价格指数预测模型。
本文用到的模型检测方法主要有相关系数法、怀特检验。
模型修正方法有科克伦—奥克特迭代方法、逐步回归法。
关键词:食品价格指数多因素分析预测模型模型检测与修正一、文献综述众所周知,食品在我国CPI中的权重约为1/3,是我国CPI 8项分类指数中权重最大的,食品价格由于受需求和供应变化影响经常出现波动,导致我国CPI指数的上升或下跌。
分析我国食品价格指数的影响因素,对于调控市场价格总水平具有重要意义。
曾经,有一种说法,叫做“CPI的走势是由猪决定”。
这句话乍一看很荒谬,但是仔细分析,其实是有道理的,猪肉的价格会首先影响粮食价格指数,粮食价格指数通过影响食品价格指数,进而影响CPI。
从公布的数据来看,食品类价格依然领涨CPI。
7月份中国食品类价格同比上涨14.8%,影响价格总水平上涨约4.38个百分点。
其中,猪肉价格同比上涨56.7%,影响价格总水平上涨约1.46个百分点。
中国社会科学院宏观经济研究所袁钢明教授表示,虽然CPI的涨幅比上个月提高0.1个百分点,但上涨幅度明显减缓,这主要是因为食品价格、尤其是猪肉价格的下降。
2009年11月份CPI由负转正,结束了九个月的负增长过程。
自此以来,CPI持续高速增长,最高时在去年7月份达到了%6.5.从数据上看,中国经济似乎已经呈现“高通胀,高增长”的过热趋势,有关经济是“过热”还是“通胀”的议论已经不绝于耳。
中国经济增长显然“过热”。
经济过热发生时,其生产能力无法跟上日益增长的总需求。
这是普遍的特点是一个不可持续的高比率的经济增长速度。
经济处于景气时期往往是经济过热的特色。
经济过热给社会各方面造成的影响是不可忽视的。
从过去的CPI数据中可以看出,食品价格的上涨是CPI的主要推手。
计量经济学国内生产总值1978-2013eviews建模分析
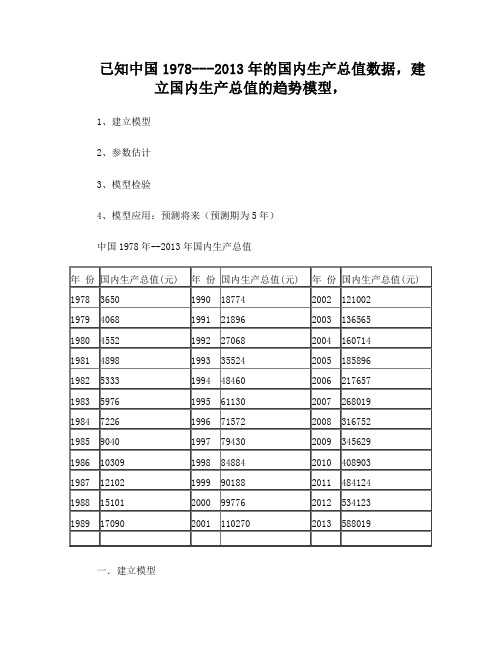
已知中国1978---2013年的国内生产总值数据,建立国内生产总值的趋势模型,1、建立模型2、参数估计3、模型检验4、模型应用:预测将来(预测期为5年)中国1978年--2013年国内生产总值一.建立模型设原始模型为:Y=α+βX+U其中,模型中X、表示年份,Y表示国内生产总值,U表示模型的随机误差。
1、数据的录入进入EViews窗口,新建一个Workfile,在命令窗口输入“data x y”,进行数据输入。
2、在命令窗口中输入“data X Y”,显示出X、Y数据二、参数估计利用 Eviews 进行 OLS 估计,得到结果如图所示:Y=--26426815+13307.46X+U图示查看y与x的关系,如图:三、模型检验(1)拟合优度检验从回归估计的结果看,模型拟合较好。
由于可决系数 R2 =0.737908,表明模型在整体上拟合的非常好。
(2)t 检验回归方程中, t 查表可得,在 5%的显著水平下,自由度 n- 2=34 的 t 的临界值是 2.032,计算得到的t=9.783933的值大于临界值,说明年份对GDP的影响是显著,通过检验。
(3)自相关性检验回归方程中, D.W.=0.061112,n=36,k’=2. 查表可知5%的显著水平下,dl=1.35,du=1.59 , 而 0<0.061112<dl=1.35,故存在自相关。
模型修正再对修正后的模型用拉格朗日乘数法进行检验修正后的1.044611,该值小于显著性水平为5%,自由度为2的分布的临界值(2)=5.991,由此可以判断模型不再存在相关关系。
(4)异方差检验14.53097,该值大于显著性水平为5%,自由度为2的分布的临界值(2)=5.991,由此可以判断模型存在异方差。
模型修正——加权最小二乘法四、模型应用:预测将来5年可以得到未来五年的预测值:374402.4、387709.8、401017.3、414324.8、427632.2。
我国粮食生产与相关投入计量经济学模型分析(1)

我国粮食生产与相关投入计量经济学模型分析一. 理论分析 二. 建立模型以1980——2003年各年粮食产量作为被解释变量,解释变量中,包括农 业化肥施用量,粮食播种面积,成灾面积,农业机械总动力,农业劳动力。
模型设定为^01122334455Y X X X X X ββββββ=+++++其中 Y :粮食产量(万吨) X1:农业化肥试用量(万吨) X2:粮食播种面积(千公顷) X3:成灾面积(千公顷) X4:农业机械总动力(万千瓦) X5:农业劳动力(万人)显著性水平α=0.05 三. 估计参数假定模型中随机项满足基本假定,用OLS 法估计参数,估计结果如下:Dependent Variable: Y Method: Least Squares Date: 12/15/06 Time: 00:16 Sample: 1980 2003 Included observations: 24C -5410.500 21545.50 -0.251120 0.8046 X1 8.164618 1.611512 5.066433 0.0001 X2 0.163901 0.151925 1.078830 0.2949 X3 -0.230792 0.103152 -2.237399 0.0381 X4 -0.251621 0.131538 -1.912919 0.0718 R-squared0.922443 Mean dependent var 42847.33 Adjusted R-squared 0.900899 S.D. dependent var 5325.186 S.E. of regression 1676.383 Akaike info criterion17.89898 Sum squared resid Schwarz criterion18.19350 Log likelihood -208.7878 F-statistic 42.81740 估计方程为^123455140.58.160.160.230.250.64Y X X X X X =-++--+t: (-0.25) (5.07) (1.08) (-2.24) (-1.91) (1.49)2R =0.9224 F=42.8174由于2X ,4X ,5X 未通过t 检验,而且4X 前的符号经济意义也不合理,因此解释变量键可能存在多重共线性。
(实习报告模版)我国粮食生产与相关投入的计量模型分析
我国粮食生产与相关投入的分析09丁颖班摘要:“民以食为天”,粮食是宝中之宝,世界上任何国家都注重粮食生产,我们中国也不例外,中国以7%的土地养活了世界22%的人口,取得举世瞩目的成果。
但是应该清醒地看到,在生产实践过程中存在不少问题,制约了我国粮食生产安全。
本文将从农业化肥施用量、粮食播种面积、成灾面积、农业机械总动力、农业劳动力等几个方面分析,应用计量模型,分析得出粮食生产函数,比较分析农业化肥施用量、粮食播种面积、成灾面积、农业机械总动力、农业劳动力对粮食生产的不同影响,并提出相应的政策建议。
关键字:粮食生产影响因素经济模型政策建议1文献综述李子奈教授(1999)[1]采用了农用化肥施用量、粮食播种面积、成灾面积、农业机械动力农业劳动力五个指标,根据1983~1995 我国的粮食生产数据拟合出了关于我国粮食生产的线性回归模型。
赵俊晔、李秀峰、王川(2006)[2]采用逐步回归和灰色关联分析的方法对1991~2004 年影响我国粮食产量变化的主要因素进行了分析,发现有效灌溉面积与粮食产量一直保持高的关联度,成灾面积与粮食产量的关联度仅次于有效灌溉面积,在此基础上对提高我国粮食生产科技支撑能力、稳定发展粮食生产提出了建议。
朱再清、陈昉源(2006)[3] 利用湖北省1993 年和2003 年粮食生产的截面数据,运用OLS 法建立1993 年和2003 年湖北省粮食产量的回归模型,就不同时期粮食生产投入要素对产出的弹性进行了比较分析,找出了弹性变化的内在原因及粮食生产中存在的问题,并提出了相应的对策。
梁子谦、李小军(2006)[4]选取了15 个指标,通过建立因子分析模型,对中国粮食单产和播种面积的影响因子进行了实证分析,研究结果表明,对粮食单产影响最大的因子是科技进步水平,其次是物质投入因子、环境与气候因子和政策因子;对粮食播种面积影响最大的因子是资源及科技因子,其次是比较效益及政策因子。
贾金荣、朱捷(2007)[5]通过分析认为,在农村经济获得一定发展并全面引入市场经济机制和随着我国成功入世之后,家庭联产承包责任制下我国粮食生产的激励机制已经失效,政府必须尽快构建适应市场经济体制的激励机制,以保证我国粮食生产水平的稳定和提高。
实验 Eviews的基本使用线性回归模型的估计和检验
实验一 Eviews 的基本使用、线性回归模型的估计和检验实验目的与要求:熟悉Eviews 软件基本使用功能、掌握线性回归模型的参数估计及其检验。
实验内容:建立一个工作文件、数据的输入、数据的保存、生成新序列、 作序列图和相关图。
线性回归模型的参数估计及其检验。
实验步骤:(具体步骤同学们可按照课堂讲解的程序进行也可按下面的指导操作,无论怎么操作,只要得到正确的结果即可) 一、模型的构建表 2002年中国各地区城市居民人均年消费支出和可支配收入 作城市居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)的散点图,如图从散点图可以看出居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)大体呈现为线性关系,4000600080001000012000Y所以建立的计量经济模型为如下线性模型: 12i i i Y X u ββ=++ 二、估计参数利用EViews 作简单线性回归分析的步骤如下: 1、建立工作文件首先,双击EViews 图标,进入EViews 主页。
在菜单一次点击File\New\Workfile ,出现对话框“Workfile Range ”。
在“Workfile frequency ”中选择数据频率: Annual (年度) Weekly ( 周数据 )Quartrly (季度) Daily (5 day week ) ( 每周5天日数据 ) Semi Annual (半年) Daily (7 day week ) ( 每周7天日数据 ) Monthly (月度) Undated or irreqular (未注明日期或不规则的)在本例中是截面数据,选择“Undated or irreqular ”。
并在“Start date ”中输入开始时间或顺序号,如“1”在“end date ”中输入最后时间或顺序号,如“31”点击“ok ”出现“Workfile UNTITLED ”工作框。
利用Eviews软件进行分析预测的案例教材
预测九江2011年棉花需求量九江古称江州、浔阳、柴桑、汝南、湓城、德化,有江西北门之称。
境内京九铁路、合九铁路、铜九铁路等铁路线贯通。
交通十分便利。
她右邻鄱阳湖,左连洞庭水,京九铁路与长江黄金水道在这里构成了中国南北、东西交流的轴心,是中国历史悠久的著名旅游城市。
长江边上的九江交通便利,铁路、公路、水运、民航齐全。
九江人杰地灵,物华天宝,旅游资源极其丰富,便利的水陆交通曾促进了中华经济、文化的发展,使享有“三江之口,七省通衢”的九江成为天下“眉目之地”。
发达的水陆交通使具有两千余年历史的九江一度成为军事重镇及商业、文化交流中心。
九江是亚热带季风性湿润气候,阳光充足,气候宜人,土地肥沃,自古以来就是著名的古代四大米市之一,因此在九江长期发展过程中农业占有很大一部分。
随着1998年的洪灾,九江农业发展受到一定阻碍,但总体上是不断繁荣发展的。
棉花原产自印度,引入中国后大面积发展,棉花喜光,要求土地肥沃,气候温暖,九江正适合种植棉花。
九江第二产业所占比重高,主要以石化,钢铁等工业为主,其次以庐山为核心的旅游产业也为九江带来丰富的收入,因此农业发展比较滞后。
由于不是大面积种植,加上九江经济还有很大的经济发展空间消费水平不高,因此九江本地种植的棉花基本能满足自身需要,下面我就罗列一下近十年来九江对棉花的需求量,并利用线性方程去预测九江2011年棉花需求量。
如下表格(单位:万吨):时间2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 (X)需求量5.04 4.56 5.34 5.87 5.876.407.148.219.12 9.61 (Y)从表中可以看出除了2002年棉花需求量有所降低外,其它年份需求都是在增长,总趋势是向上积极的。
2006年以前,棉花需求量一直在增长但增速比较慢,不是非常明显,2006年到2009年其增速呈“狂飙”式,几乎一年增长一万吨,但到2010增速有所减缓,其增长情况应该是跟九江整体经济发展情况相对应的,也反映了这几年九江的经济运行状况。
农产品产量影响因素分析和模型检验.doc
农产品产量影响因素分析和模型检验摘要:文章运用计量经济学的方法分析影响农产品产量(这里主要是种植业)的影响因素,即通过对农作物总播种面积、受灾面积、农用化肥施用量、乡村人口、有效灌溉面积、农产品生产价格指数、农业生产资料指数、农业机械总动力、乡村从业人员的实证分析,运用经济学原理,引入计量经济学模型,得出从改革开放到2011年我国农产品产量的影响因素,并作出分析,提出建议。
关键词:农产品(种植业)总产量影响因素实证分析1、问题的提出1978年,我国的改革开放从农业开始,以家庭联产承包责任制拉开了改革的序幕。
农业在我国经济中有着举足轻重的地位,只有在农业的基础上才有工业的发展,只有在农业和工业发展的基础上,才有第三产业的繁荣兴盛。
可见,农业是“母亲产业”,是国民经济的基础。
改革开放以来,国家大力出台政策支持农村的改革――从家庭联产承包责任制到调整农村的产业结构和流通体制,然后到农村市场经济的改革,然后到取消农业税,在各个阶段都取得了良好的效果,农业总产值一直持续增加。
其中种植业作为农业的基础和农业最重要的一个组成部分,并且包含着人民群众最重要的生产资料――粮食,所以对影响种植业农产品产量的因素分析是十分有必要和有意义的。
本文将通过计量经济学的方法对改革开放以来影响农产品产量的因素进行分析,来揭示我国农业中种植业现存的一些问题,力求针对问题,找到解决的办法。
2、理论综述中国是农业大国,自古以来,无论阶级关系如何变化,农民始终是我国的主要生产动力,农业始终是我国国民经济的基础,其总产值直接影响到我国粮食安全。
学术界历来十分重视对三农问题的研究,并取得了一定的成果。
如:林毅夫(1994)、黄少安(2005)等,从制度经济学角度研究了我国农业问题,认为农村的经济体制改革对我国农业总支出的增加起到了至关重要的作用。
郝利等运用柯布道格拉斯生产函数,建立了农业科技进步贡献率测算模型,对北京市1990-2007年农业科技进步贡献率进行测算,得出的结论是1999-2007年北京科技农业贡献率为78.32%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我 国是传 统 的农 业 大 国 。农 业 生产 关 系到 民生 和其 他相关 产业 的发 展 。自改革 开放 以来 , 国农 产 我 品产 量不 断提 高 , 民温 饱 已基本解 决 , 人 但粮食 生 产 不能 放松 , 必须长 期 作为 国家 的头等 大事 。 了对我 为 国 粮食 发 展进行 规 划 ,需要 定 量地 分析 影 响 中国粮 食产 量的主 要因素 。 1 数据来 源 以 1 8 0 5年 国研 网收 集 的农 产 品 的相关 数 9 4 2o
劳动力和 国家财政用于农业的支出, 数据见表1 。
裹 1 农 产 品 产 ■ 与 相 关 投 入量
模型初步设定为:
Y r (唯 祁 祁 C
其 中 ,,农 产 品产 量 ( 吨 ) : 业 化 肥施 用 l: 万 , 农 。 量 ( 吨 ) : 万 , 农产 品总 播种 面积 ( 千公 顷 ) : 灾 , 成
3 9
21 O O年 5月
情 报 探索
第 5 ( 11 ) 期 总 5期
面积( 千公 顷 )x : ,4农业 机 械 总动 力 ( 万千 瓦 )墨 : , 农 业 劳 动 力 ( 人 )X : 万 ,6国家 财 政 用于 农 业 的支 出 ( 亿 元 )显著 性水 平 o 00 。 , r . = 5 3 参数 估计 假定 模 型 中 随机 项满 足 基本 假定 , O S法估 用 L 计参 数 , 计结 果如 图 1 示 : 估 所
l= .3 宰Xl O3 6 0 木X202 0 2 ’ , 53 3 4 = + .1 - .7 I c
X3 0 9 2 2} 广 3 9 . 1 + .6 18 04 0 2
对数似然值
德 宾 瓦 森 统 计
一 7. 7 F 19 0 9 8 统计量
因变 量 : Y 方 法 : 小 二 乘 法 最
样 本 :94 2 0 18 - 0 4
回归 , 表 3 得 。 由表 3可知 ,解 释变 量 的重 要 程 度依 次 为 、
l 、 、 、 。 、 墨 墨 2 43 oL . S法 估 计
将 各解 释变 量按 以上 顺 序分别 引入基 本 回归模 型 中 , 用 O S法估 计 。 并 L 先把 引入模 型 , y关 于 。 做 回 用 , 孔 归并 用 O S法 估计 得 : L
Y: .3 3 4 6 木X。04 3 7 9 8 7 3 94 161 0 一 .0 7 1 X42 9 . 9 3 + 9 1 021 7 R208 29 7 t7 1 5 3 7; 4 1 37 9; _ = .7 2 : .8 8 一 .1 4
21 0 0年 5月
情 报 探 索
第 5期 ( 1 1 ) 总 5期
基于 E i s Ve 的我国农产品产量与 w 相关投入的模型分析与预测检验
昊琦 磊
摘
邓金 堂
6 10 ) 2 02
( 西南科技 大 学经济 管理学院 四川绵 阳
入 的模 型 , 对模 型 进 行 了识 剐 , 并 最后 对 模 型 进 行检 验 , 证 其 可行 性 。 验 关键 词 :Vi E e ws 农 产 品 模 型 分析 预 测检 验
要 : 我 国 1 8" 0 5年 的农 产 品相 关数 据 进 行 收 集和 分 析 , 用 E i 软 件 进 行 计 算 , 立 了农 产 品 产 量 与 相 关投 对 9 4' 0 - 2 运 Ve ws 建
中 图分 类 号 :l Sl
文献 标 识 码 : A
文 章编 号 :0 5 8 9 (0 0 0 - 0 9 0 10 — 0 52 1 )5 0 3- 3
回归误差 残 差 平 方 和
15 74 0 A C信息准则值 5 .9 I 3 6 6 施 瓦 茨 准 则 值 39 086
1 .4 9l 81 8 1 . 3 310 94
O O o 0o .0 O
可见 , 引入 五 后 , 拟合 优度 有所 提高 , 但 蜀 回归 参 数 的符 号不 对 。所 以应 该把 墨 从 模 型 中删 除 。 按 照 上面 的方 法 依 次 引 入 墨 , , , , 经 过检 验均 可保ቤተ መጻሕፍቲ ባይዱ留 。 删去 不 符 合条 件 的解 释变 量 , 到 l 得 , 关 于 - , , 的方 程 : , 2
据 为依据 进行 模 型的建 立 。 外 , 另 因为要 对模 型 的可 行 性 进行 检 验 , 以把 2 0 所 0 5年 的数 据 空 出 , 为模 作 型 的检验 数据 。 2 模型 建 立 这 里 以 18  ̄0 4年各 年农 产 品产 量作 为被 解 94 20 释变量 , 经分析 , 以下解释变量 : 化肥施用量 、 得到 农业 农产 品总播 种面积 、 成灾 面积 、 业机 械总动 力 、 农 农业
收稿 日期 :0 9 1 — 7 2 o — 1 0 作者 简 介 : 琦磊 (9 3 ) 男 , 吴 I8 一 , 情报 学 专 业 2 0 研 究 生 , 究 方 向 为 经 济 信 息 与信 息 经 济 学 ; 0 7级 研 邓金 堂 (93 ) 男 , 士后 , 16 一 , 博 教 授 , 士 生 导 师 , 究方 向 为 高 技 术 经 济 、 本 市 场 与 自主创 新 等 。 硕 研 资
2 .2 4 42 5 3 。
所 包 含 的观 察 量 :1 2
R平 方 调 整 后 的 R平 方
09 25 2 .8 1 因变 量 均 值 09 50 8 .7 1 因变 量 标 准 差
6 6 -5 4 3 13 9 8 39 6 5 .1
1 .o0 4 78 7
1 O 0 通 过 F统 计 量 的 概 率 . 25 9 9 图 1 最 小二 乘 法 参 数 计 算
