运筹学 单纯形法1
合集下载
运筹学单纯形法
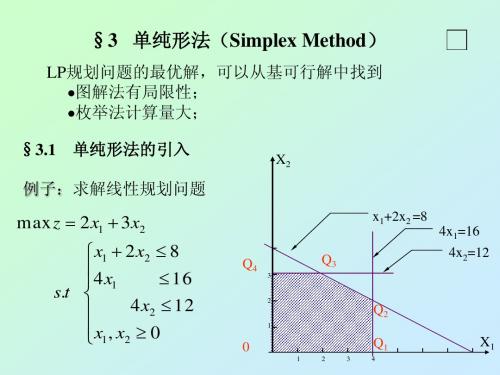
只要取 x5=min{-，8/2，12}=4 就有上式成立。 x5=4时， x4=0，故决定用x5换x4 x1 =4- 1/4 x4 x5 =4-1/2 x4 +2 x3 x2 =2+1/8 x4–1/2 x3 代入得 z=14-3/2 x3 –1/8 x4 ，令x3 ，x4=0得z=14。新基可 行解为 X(3) =(4,2,0,0,4) T –为最优解，新顶点Q2 最优目标值z=14 。
§3.4 最优性检验和判别定理
线性规划解的四种可能： 1、有唯一解； 2、无穷多最优解； 3、无界解； 4、无可行解。 何时达最优解, 何种最优解？
将基本可行解X(0)和X(1)分别代入目标函数得
z z
(0)
= ∑ ci xi0
i =1 m
mቤተ መጻሕፍቲ ባይዱ
(1)
= ∑ ci [ xi0 − θ aij ] + θ ci
§3.3 从初始基可行解转换为另一基可行解
0 0 记初始基可行解为X(0),有 X ( 0 ) = (x10 x 2 L x m 0 L 0
)
Pi xi0 = b 该解满足约束方程, 即 ∑
i =1
m
(1)
非基向量可以用基向量的线性组合表示
Pj = ∑ aij Pj
i =1 m
m
(2) (3)
Pj − ∑ aij Pj = 0
从实际例子中分析单纯形法原理的基本框架为 •第一步：将LP线性规划变标准型，确定一个初始可行解 （顶点）。 •第二步：对初始基可行解最优性判别，若最优，停止；否 则转下一步。 •第三步：从初始基可行解向相邻的基可行解（顶点）转 换，且使目标值有所改善—目标函数值增加，重复第二和 第三步直到找到最优解。
运筹学
1（单纯形法）例：Min Z=-2x1-x2+x3 , s.t. 3x1+x2+x360≤x1-x2+2x310≤,x1+x2-x320≤,xj 0≥,解析：对第一、二、三个不等式添加松弛变量x4 x5 x6,则原线性问题化成标准形形式为：（略）因为B=（A4 A5 A6）是一单位矩阵，且b=(60 10 20)T>0 所以基B 是可行基，x4 x5 x6为基变量，x1 x2 x3为非基变量，基B 对应的基本可行解为检验数02>=ξ，故当前解不是最优解，A1列中有三个元素a11 a21 a31 均为正数，取min ()313212111,,a b a b a b =min ()120110360,,=10故转轴元为a21,x1为进基变量，x5为出基变量，进行旋转后得下表（略）它对应的基本可行解为x=(10 0 0 30 0 10)T,其目标函数值为Z0=-20，但,032>=ξ仍不是最优解，（以下的过程跟前面一样）最后得Z0=-35，检验向量0<ξ故为最优解。
故基本可行解x*=(15 ,5 ,0 )Tm 目标函数值为Z0=-35。
2（两阶段法）例 max z=3x1+4x2+2x3 s.t. x1+x2+x3+x430≤, 3x1+6x2+x3-2x40≤, x24≥解：化为标准形形式为min z=-3x1-4x2-2x3 s .t.分别加x5 x6 x7松弛变量，因为该线性规划的系数矩阵的系数矩阵已包含两个单位向量，就是A5=（100）T ，A6=（010）T ，第一阶段只要增加一个人工变量x8得到辅助LP 问题为min g=x8 s.t .以下略，作如下表（略），将表中第三行加到关于g 的第0行中，得到第一张单纯形表（略）按单纯形迭代，表略，第一阶段结束，得到辅助问题的一个最优解，3（对偶单纯形法）例 min 2x1+3x2+4x3, s.t. x1+2x2+x33≥ 2x1-x2+3x34≥ x1 x2 x3 0≥,解：引进非负的剩余变量x40≥,x50≥,将不等式约束化为等式约束直接利用对偶单纯形法求解，b2=- 4<b1=-3,所以x5为出基变量，由以下比值决定进基变量min(3422,----)=21a ξ=1,所以x1为进基变量，以a21为转轴元进行旋转变换得下表（略）因为b1=-1<0,所以x4为出基变量，因为min( )所以x2为进基变量，以a12为转轴得表（略）此时b>0,故原问题最优解为x*=( )T,其最优值Z0=（） 4写出下面线性规划的对偶规划。
运筹学课件1-4单纯形法计算步骤
b 21 4
9 4
3 x1 1 -1 3 4 -1 12
9 x2 3 1 9 0 1 0
0 x3 1 0 0 1 0 0
0 x4 0 1 0 -3 1 -9
θ 7 4
9/4 -
所以把x3换出为非基变量，x1为换入变量即新的基变量。
第20页
cj
CB 0 0
0 9 3
XB x3 x4 cj-zj x3 x2 cj-zj x1
cj-zj
x3 x1 x5 cj-zj
6
0 1 0
5
5/2 1/2 1
0
1 0 0
0
-1/2 1/2 -1
0
0 0 1
75 5
0
2
0
-3
0
5
x2
5
0
1
0
-1
1
第10页
cj CB 0 0 0 0 6 0 XB x3 x4 x5 b 90 75 80 105/2 75/2 5
6 x1 1 2 2
5 x2 3 1 2
9/4
-
3 9
9/4 25/4
1 0 0
25
第24页
cj CB 0 0 XB x3 x4 cj-zj b 21 4
3 x1 1 -1 3
9 x2 3 1 9
0 x3 1 0 0
0 x4 0 1 0 θ 7 4
0
9
x3
x2 cj-zj x1 x2 cj-zj
9
4
4
-1 12
0
1 0 0 1 0
1
0 0 1/4 1/4 -3
i 1
第1页
单纯形表求解线性规划问题
运筹学单纯形法的计算步骤
b2
0… 0
a2,m+1
…
a2n
2
…
…
…
…
cm xm
bm
0… 1
am,m+1
…
amn
m
-z -z 值 0 … 0
m+1
…
n
XB 列——基变量， CB 列——基变量的价值系数(目标函数系数) cj 行——价值系数，b 列——方程组右侧常数 列——确定换入变量时的比率计算值
下面一行——检验数， 中间主要部分——约束方程系数
(4).根据max(j > 0) =k，拟定xk为换入变量，按 规则计算 =min{bi/aik\aik>0}
可拟定第l行旳基变量为换出变量。转入下一步。
(5).以 alk 为主元素进行迭代(即用高斯消去法或称为旋转变 换)，把 xk 所对应的列向量变换为(0，0，…，1，…，0)T，将
XB 列中的第 l 个基变量换为 xk，得到新的单纯形表，返回(2)。
b
x1
x2
x3
x4
x5
2 x1 2 0 x4 8 3 x2 3
1
0
1
0 -1/2 -
0 0 -4 1 (2 ) 4
0 1 0 0 1/4 12
-z
-13
0
0 -2
0 1/4
X(2)=(2，3，0，8，0)T， z2 =13
cj
2 30 0 0
CB XB
b
x1
x2
x3
x4
x5
2 x1 4 0 x5 4 3 x2 2
量，给出第一阶段的数学模型为：
min = x6+x7
x1-2x2+x3+x4
运筹学-第一章-单纯形法基本原理
初始基本可行解：
X ( 0) ( x1 , x2 ,, xm ,0,0,...,0)T (b1 , b2 ,......,bm ,0,0,...,0)T
0
0
0
单纯形法基本原理
2、基变换 定义：两个基可行解称为相邻的，如果它们之间变换 且仅变换一个基变量。 初始基可行解的前m个为基变量，
X
凸集
顶点
凸集
不是凸集
顶点：如果凸集C中不存在任何两个不同的点X1，X2，使X 成为这两个点连线上的一个点
单纯形法基本原理
定理1：若线性规划问题存在可行解，则该问题的可行域是 凸集。 定理2：线性规划问题的基可行解X对应可行域(凸集)的顶 点。 定理3：若问题存在最优解，一定存在一个基可行解是最优 解。（或在某个顶点取得）
的左边变成一个单位矩阵，
b (b1 a1 j ,.,bl 1 al 1 j , , bl 1 al 1 j ,.,bm am1 j , ) ( x1 , x2 ,..., xl 1 , x j , xl 1 ,..., xm )
X
(1)
T
与X
( 0)
是相邻的基可行解。
M M bm 0 L
M M
M M
L 1 am,m1 L L 00
M , M amn m
bi 其中： i a kj 0 a kj
j c j ci aij c j z j
单纯形法的计算步骤
例1.12 用单纯形法求下列线性规划的最优解
max Z 3 x1 4 x 2 2 x1 x 2 40 x1 3 x 2 30 x , x 0 1 2
xi0 aij 0, aij 0,取值无限，
X ( 0) ( x1 , x2 ,, xm ,0,0,...,0)T (b1 , b2 ,......,bm ,0,0,...,0)T
0
0
0
单纯形法基本原理
2、基变换 定义：两个基可行解称为相邻的，如果它们之间变换 且仅变换一个基变量。 初始基可行解的前m个为基变量，
X
凸集
顶点
凸集
不是凸集
顶点：如果凸集C中不存在任何两个不同的点X1，X2，使X 成为这两个点连线上的一个点
单纯形法基本原理
定理1：若线性规划问题存在可行解，则该问题的可行域是 凸集。 定理2：线性规划问题的基可行解X对应可行域(凸集)的顶 点。 定理3：若问题存在最优解，一定存在一个基可行解是最优 解。（或在某个顶点取得）
的左边变成一个单位矩阵，
b (b1 a1 j ,.,bl 1 al 1 j , , bl 1 al 1 j ,.,bm am1 j , ) ( x1 , x2 ,..., xl 1 , x j , xl 1 ,..., xm )
X
(1)
T
与X
( 0)
是相邻的基可行解。
M M bm 0 L
M M
M M
L 1 am,m1 L L 00
M , M amn m
bi 其中： i a kj 0 a kj
j c j ci aij c j z j
单纯形法的计算步骤
例1.12 用单纯形法求下列线性规划的最优解
max Z 3 x1 4 x 2 2 x1 x 2 40 x1 3 x 2 30 x , x 0 1 2
xi0 aij 0, aij 0,取值无限，
运筹学单纯形法
加松弛变量Xs
AX+IXs=b
X≥0
X,Xs≥0
-x1+x2+4x3≤2 (引入松弛变量x4) -x1+x2+4x3+x4=2 松弛变量的意义：未被充分利用（剩余）的资源， 松弛变量的价格系数是0（c4=0）。
(3) -x1+x2+4x3≥2 (引入剩余变量x5) -x1+x2+4x3-x5=2 剩余变量的意义：超用的资源（c5=0）
运筹学
Operations Research
2.2 单纯形法
2.2.1 线性规划模型的标准形式
一、标准型要求：
（1）目标最大化（max） （2）约束是“=”约束 （3）右端项非负 （4）所有变量非负 标准型
二、非标准型化为标准型
(1) min CX
加负号
max(-CX)
min z=2x1+4x2 (令z’=-z) max z’=-2x1-4x2 (2) AX≤b
例2：将下面的线性规-x1，x3=x3’-x3”，增加松弛变量x4， 增加剩余变量x5。
(4) xj≤0
( 令 xj’= -xj )
x j ’≥ 0
(5) xj为自由变量
( 令xj=xj’-xj’’ )
xj’≥0, xj’’≥0
例1：在煤电油例中，其线性规划模型为： maxz = 7x1+12x2 9x1+ 4x2≤360 4x1+ 5x2≤200 s.t. 3x1+10x2≤300 x1,x2≥0 化标准型：增加松弛变量x3、x4、x5 maxz = 7x1+12x2+0x3+0x4+0x5 9x1+ 4x2 +x3 =360 +x4 =200 s.t. 4x1+ 5x2 3x1+10x2 +x5 =300 x1,…,x5≥0
AX+IXs=b
X≥0
X,Xs≥0
-x1+x2+4x3≤2 (引入松弛变量x4) -x1+x2+4x3+x4=2 松弛变量的意义：未被充分利用（剩余）的资源， 松弛变量的价格系数是0（c4=0）。
(3) -x1+x2+4x3≥2 (引入剩余变量x5) -x1+x2+4x3-x5=2 剩余变量的意义：超用的资源（c5=0）
运筹学
Operations Research
2.2 单纯形法
2.2.1 线性规划模型的标准形式
一、标准型要求：
（1）目标最大化（max） （2）约束是“=”约束 （3）右端项非负 （4）所有变量非负 标准型
二、非标准型化为标准型
(1) min CX
加负号
max(-CX)
min z=2x1+4x2 (令z’=-z) max z’=-2x1-4x2 (2) AX≤b
例2：将下面的线性规-x1，x3=x3’-x3”，增加松弛变量x4， 增加剩余变量x5。
(4) xj≤0
( 令 xj’= -xj )
x j ’≥ 0
(5) xj为自由变量
( 令xj=xj’-xj’’ )
xj’≥0, xj’’≥0
例1：在煤电油例中，其线性规划模型为： maxz = 7x1+12x2 9x1+ 4x2≤360 4x1+ 5x2≤200 s.t. 3x1+10x2≤300 x1,x2≥0 化标准型：增加松弛变量x3、x4、x5 maxz = 7x1+12x2+0x3+0x4+0x5 9x1+ 4x2 +x3 =360 +x4 =200 s.t. 4x1+ 5x2 3x1+10x2 +x5 =300 x1,…,x5≥0
运筹学第5章 单纯形法
0 0 1
在第一次找可行基时，所找到的基或为单位矩阵或为由单位矩阵的 各列向量所组成，称之为初始可行基，其相应的基本可行解叫初始基 本可行解。如果找不到单位矩阵或由单位矩阵的各列向量组成的基作 为初始可行基，我们将构造初始可行基，具体做法在以后详细讲述。
8Leabharlann §1 单纯形法的基本思路和原理
二、 最优性检验 所谓最优性检验就是判断已求得的基本可行解是否是最优解。
5
§1 单纯形法的基本思路和原理
线性规划解之间的关系：
1.可行解与最优解： 最优解一定是可行解，但可行解不一定是最优解。
2. 可行解与基本解： 基本解不一定是可行解，可行解也不一定是基本解。
3. 可行解与基本可行解： 基本可行解一定是可行解，但可行解不一定是基本可行解。
4. 基本解与基本可行解： 基本可行解一定是基本解， 但基本解不一定是基本可行解。
9
§1 单纯形法的基本思路和原理
2.最优解判别定理
对于求最大目标函数的问题中，对于某个基本可行解，如
果所有检验数 j≤0，则这个基本可行解是最优解。 下面我
们用通俗的说法来解释最优解判别定理。设用非基变量表示
的目标函数为: z z0 j xj jJ 由于所有的xj的取值范围为大于等于零，当所有的 j都小
由线性代数的知识知道，如果我们在约束方程组系数矩阵中找
到一个基，令这个基的非基变量为零，再求解这个m元线性方程组就
可得到唯一的解了，这个解我们称之为线性规划的基本解。
在此例中我们不妨找到
1 1 0 B3 1 0 0
为A的一个基，令这个基的非
1 0 1
基变量x１，s2为零。这时约束方程就变为基变量的约束方程：
第五章 单 纯 形 法
运筹学单纯形法
单纯形表
max z=x1+2x2 s.t. x1+x23 x2 1 x1, x2 0
Cj CB XB b 0 0 Z X3 3 X4 1 0 1 2 0 0
标准化
max z=x1+2x2 s.t. x1+x2+ x3 =3 x2 +x4=1 x1, x2 ,x3, x40
X1 X2 X3 X4 1 0 1 1 1 2 1 0 0 0 1 0
Z=x1+2x2 x1+x2+ x3 =3 x2 +x4=1 单纯形表
Cj
1
2
0
0
单纯形法原理 单纯形表 CB XB b
z=x1+2x2 x3 =3-x1-x2 x4=1 -x2
x2进基，x4离基
X1 X2 X3 X4
3/1 11
0
1 0
1 1
1 1
2 2 0 1 0 2 0 1 0 0 1 0 -1 0
max z=x1+2x2 s.t. x1+x2+x3 =3 x2 +x4=1 x1, x2, x3, x40
x1=0
(x1,x2,x3,x4)= (0,1,2,0), z=2 C (x1,x2,x3,x4)= (2,1,0,0), z=4,最优解
B
x4=0 x3=0
(x1,x2,x3,x4)= (0,0,3,1), z=0
1 0
0 0
0 1
0
CB XB b 0 2 Z Cj CB XB b 1 2 Z X1 2 X2 1 4 X3 2 X2 1 2 1 1 0 0
X1 X2 X3 X4 1 0 1 1 0 0 0 -1 1 -1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2020/4/3
12
单纯形表
cj CB XB 0 x4 -M x6 -M x7
σj 0 x4 0 x2 -M x7
σj
0 x4 0 x2 -3 x1
σj
0 x4 0 x2 1 x3
σj
-3 0 1 0
bi x1 x2 x3 x4
4
1
1
1
1
1 -2 [ 1 ] -1 0
9
03
1
0
-3-2M [4M] 1 0
6 [ 6 ] 0 4 0 3 -3 1 1
[ 6] 0
40
3
-4 0 x1入，x7出
0 0 0 0 1 -1/2 1/2 -1/2 3 0 1 1/3 0 0 0 1/3 1 1 0 2/3 0 1/2 -1/2 1/6
0
0
000
-1
-1
所以：已得最优解，且人工变量为非基变量，则可 去掉人工变量，得原问题的一个即可行基。
σj 0 x4 0 x2 -1 x7
σj
0 x4 0 x2 0 x1
σj
0 0 0 0 0 -1 -1
bi x1 x2 x3 x4 x5 x6 x7 θ
4
1
1
1
1
0 0 04
1
-2 [ 1 ] -1
0
-1
1
01
9
0
3
1
0
0
0
13
-2 [ 4 ] 0 0 -1
0 0 x2入，x6出
3 3 0 2 1 1 -1 0 1 1 -2 1 -1 0 -1 1 0 －
0
C x1
x2 x3 x4 x5 Z 可行解 图中点
0 8 16 12 0 √
O
4 0 16 -4 12 ╳
A
0
无解
3 2 16 0 9 √
Q4
0 0 -16 12 16 ╳
C
0 4 0 12 8 √
Q1
0
0 无解
2 0 0 4 14 √
Q2
3 0 8 0 13 √
Q3
3 -2 0 0 17 ╳
B
max z 2x1 3x2
量
“＝” →加一个人工变量
目标函数： 人工变量的系数为“－M”，即罚因子
2020/4/3
10
若线性规划问题有最优解则人工变量必为0。
MaxZ=-3x1+x3
MaxZ=-3x1+x3-Mx6-Mx7
x1+ x2+ x3≤4
x1+ x2+ x3+x4
=4
-2x1+ x2- x3≥1 3x2+x3=9
标准化 及变形
-9/2 0
0 0 -3/4 -M+3/4 -M-1/4
2020/所4/3以：X*=(x1,x2,x3)T=(0,5/2, 3/2)T Z*=3/2
13
二、两阶段法
• 第一阶段暂不考虑原问题是否存在基可行解，给原问题加 入人工变量，并构建一个仅含人工变量的目标函数（求极 小化），人工变量的价值系数一般为1，约束条件和原问 题的一样。
0
2 0 -1
θ -
50
x1入，x4出
因为σ2 = 2,且ai2 全≤0
所以：无界
2020/4/3
22
例3: 下表为一极大化问题对应的单纯形表
x1
x2
x3
x4
x5
bi
x1
1
0
a1
0
a2
a6
x2
0
1
1
0 -2 2
x4
0
0
-2
1
a3
3
σj
0
0
a4
0
a5
讨论在a1,a2,a3,a4,a5,a6取何值的情况下，该表中的解为：
40
σj
40 45 25
0
0 x2入，x4出
……
45 X2 80/3 1/3 1
0 2/3 -1/3
25 x3 20 1 0 1 -1 1
σj
0
0 0 -5 -10
因为全σj ≤ 0,且σ1=0,则有无穷多最优解。
所以：其中一个最优解为X*=(0,80/3,20,0,0) T,Z*=1700
2020思/4/3考：无穷多最优解的一般形式？ 21
B:(1,3/2)
2020/4/3
0: (0,0)
x1 A: (87/5,0)
回顾：单纯形法求解步骤：
2020/4/3
8
第5节 单纯形法的进一步讨论
2020/4/3
9
第5节 单纯形法的进一步讨论
一、人工变量法（大M法）
约束条件：
“≤” →加一个松弛变量 “≥” →减一个剩余变量后，再加一个人工变
x1 2x 2 x3
8
4x1
x4 16
4 x2
x5 12
x j 0, j 1, ,5
3
• Step2：检查非基变量所对应的检验数σj，若所有的σj≤0，则当 前的基可行解就是最优解，当前的目标函数值就是最优值，停 止计算。
• 否则，转入下一步。
• SP算tke≤。p03(即：P若k中存每在一一个个分σk>量0a，ikσ≤k0所)，对则应该的L变P无量有xk限的最系优数解列，向停量止计 • 否则，转入下一步。
2020/4/3
16
（第二阶段）单纯形表2
cj
-3 0 1 0 0
CB XB bi x1 x2 x3 x4 x5 θ
0 x4 0
0
0
0
1 -1/2 -
0 x2 3 0 1 1/3 0 0 9
-3 x1 1
1
0 [2/3] 0 1/2 3/2
σj
0
0 [3]
0 3/2 x3入，x1出
0 X4 0
0
0
新加变量系数
xs
xa
0
-M
2020/4/3
18
第5节 单纯形法的进一步讨论
人工变量法（大M法）和两阶段法
约束条件：
“≤” →加一个松弛变量 “≥” →减一个剩余变量后，再加一个人工变
量
“＝” →加一个人工变量
若线性2020规/4/划3 问题有最优解则人工变量必为0。
19
三、单纯形法计算中的几个问题
• ⑴.要求解问题的目标函数能用数值指 标来反映，且为线性函数；
• ⑵.存在着多种方案； • ⑶.要求达到的目标是在一定条件下实
现的，这些约束可用线性等式或不等式描 述。
2020/4/3
25
建模步骤：
第一步：设置要求解的决策变量。决策变量选取得 当，不仅能顺利地建立模型而且能方便地求解，否则 很可能事倍功半。
• 目标函数极小化时解的最 当所有非基变量的σj≥0时为最优解；
优性判别；
• 无可行解的判别；
最优解中人工变量为非0的基变量时；
• 无界的判别； • 无穷多最优解的判别； • 唯一最优解的判别.
存在某个σk>0，且所有的aik≤0时；
得最优解时，有检验数为0的非基变量； 得最优解时，所有非基变量检验数为负；
第4节 单纯形法计算步骤
2020/4/3
1
Step 1 化为标准型，找出初始可行基，并列出初始单纯形表
2020/4/3
2
• 上述初始单纯形表中，最后一行称为检验数σj
x2
A 4
Q4
Q3
B
3
2
Q2
1
2020/4/3
O
1
2
3 4 Q1
基 基向量 x1 B1 P3P4P5 0 B2 P2P4P5 0 B3 P2P3P5 0 B4 P2P3P4 0 B5 P1P4P5 8 B6 P1P3P5 4 B7 P1P3P4 B8 P1P2P5 4 B9 P1P2P4 2 B1 P1P2P3 4
✓唯一最优解；
• a4<0,a5<0, a6≥0
✓无穷多最优解；
• a6≥0,a4≤0, a5≤0, a4=0或a5=0
✓无界； ✓无可行解；
✓非最优，继续换基：
• a6≥0,a5>0,a2≤0, a3≤0 • a4≤0,a5≤0, x4或x2为人工变量，a6≥0 ； x1为人工变量，a6>0 • a4>0,a4>a5;a6/a1>2→a1>0
33 0 2 1 1 -2 1 -1 0
6 [ 6] 0 4 0
[6M-3] 0 4M+1 0 00 0 0 1
3 0 1 1/3 0 1 1 0 [2/3] 0
0 0 [ 3] 0 00 0 0 1 5/2 -1/2 1 0 0
0 -M -M
x5 x6 x7 θ
0 0 04 -1 1 0 1
0 0 13
xi ≥0,j=1,2,3
-2x1+ x2-x3 -x5+x6 =1
3x2+x3
+x7=9
xi ≥0,j=1,…,7
增加人工变量后，线性规划问题中就存在一个B为单位矩阵， 后面可以根据我们前面所讲的单纯形法来进行求解。
2020/4/3
11
练习：列出初始单纯形表，并求解第2
小题的最优解
1. P55，2.2（1） 2.
3 4 1 03 [ 5 ] 2 0 1 8/5
[10] 5
0
0 x1入,x4出
0 [14/5] 1 -3/5 3/2
1 2/5 0 [1]
0 0
1/5 4
x2
-2 x2入,x3出