解答 运筹学 第一章 线性规划及其单纯形法习题
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
运筹学习题

运筹学复习题第一章 线性规划及单纯形法一、单选题1. 线性规划具有无界解是指A. 可行解集合无界B. 有相同的最小比值C. 存在某个检验数0k λ>,且0(1,2,,)ik a i m ≤=D. 最优表中所有非基变量的检验数非零 2. 线性规划具有唯一最优解是指A. 最优表中非基变量检验数全部非零B. 不加入人工变量就可进行单纯形法计算C. 最优表中存在非基变量的检验数为零D. 可行解集合有界 3. 线性规划具有多重最优解是指A. 目标函数系数与某约束系数对应成比例B. 最优表中存在非基变量的检验数为零C. 可行解集合无界D. 基变量全部大于零 4. 使函数Z=-x 1+x 2+2x 3 减小最快的方向是A. (-1,1,2)B. (1,-1,-2)C. (1,1,2)D. (-1,-1,-2) 5. 当线性规划的可行解集合非空时一定 A. 包含点X =(0,0,···,0) B. 有界 C. 无界 D. 是凸集 6. 线性规划的退化基可行解是指A. 基可行解中存在为零的非基变量B. 基可行解中存在为零的基变量C. 非基变量的检验数为零D. 所有基变量不等于零 7. 线性规划无可行解是指A. 第一阶段最优目标函数值等于零B. 进基列系数非正C. 用大M 法求解时,最优解中还有非零的人工变量D. 有两个相同的最小比值 8. 若线性规划不加入人工变量就可以进行单纯形法计算A. 一定有最优解B. 一定有可行解C. 可能无可行解D. 全部约束是小于等于的形式 9. 设线性规划的约束条件为123124222401234 (,,,)jx x x x x x x j ⎧++=⎪++=⎨⎪≥=⎩ 则非退化基本可行解是A. (2, 0,0, 0)B. (0,2,0,0)C. (1,1,0,0)D. (0,0,2,4) 10. 设线性规划的约束条件为123124222401234 (,,,)jx x x x x x x j ⎧++=⎪++=⎨⎪≥=⎩ 则非可行解是A. (2,0,0, 0)B. (0,1,1,2)C. (1,0,1,0)D. (1,1,0,0) 11. 线性规划可行域的顶点一定是A. 可行解B. 非基本解C. 非可行解D. 是最优解 12. 1234min z x x =+1212124220,x x x x x ⎧+≥⎪+≤⎨⎪≥⎩ A. 无可行解 B.有唯一最优解 C.有无界解 D.有多重最优解13. 12122124432450,max z x x x x x x =-⎧+≤⎪≤⎨⎪≥⎩A. 无可行解B. 有唯一最优解C. 有多重最优解D. 有无界解 14. X 是线性规划的基本可行解则有A. X 中的基变量非负,非基变量为零B. X 中的基变量非零,非基变量为零C. X 不是基本解D. X 不一定满足约束条件 15. X 是线性规划的可行解,则错误的结论是A. X 可能是基本解B. X 可能是基本可行解C. X 满足所有约束条件D. X 是基本可行解 16. 下例错误的说法是A. 标准型的目标函数是求最大值 B 标准型的目标函数是求最小值 C. 标准型的常数项非正 D. 标准型的变量一定要非负 17. 为什么单纯形法迭代的每一个解都是可行解?答:因为遵循了下列规则 A. 按最小比值规则选择换出变量B. 先进基后出基规则C. 标准型要求变量非负规则D. 按检验数最大的变量选择换入变量 18. 线性规划标准型的系数矩阵A m×n ,要求A. 秩(A )=m 并且m <nB. 秩(A )=m 并且m <=nC. 秩(A )=m 并且m =nD. 秩(A )=n 并且n <m 19. 下例错误的结论是A. 检验数是用来检验可行解是否是最优解的数B. 检验数是目标函数用非基变量表达的系数C. 不同检验数的定义其检验标准也不同D. 检验数就是目标函数的系数 20. 对取值为无约束的变量j x ,通常令'''j j j x x x =-,其中''',0j j x x ≥;在用单纯形法求得的解中不可能出现A. '0j x =,''0j x ≥ B. '0j x =,''0j x = C. '0j x >,''0>j x D. '0j x >,''0j x =21.运筹学是一门A. 定量分析的学科B. 定性分析的学科C. 定量与定性相结合的学科D. 定量与定性相结合的学科,其中分析与应用属于定性分析,建立模型与求解属于定量分析二、设某种动物每天至少需要700克蛋白质、30克矿物质、100毫克维生素。
运筹学思考练习题答案

5 2
1 2
}
b1
Min{
5 2
(
1 6
)}
,即
5
b1
15
,则 0
b1
20
(4)以单价 2.5 购入第一种资源是值得的,因其小于该资源“影子价格”(即 2.5<4),可盈利;
第二种资源应要价至少为 2(影子价格),否则不如自己组织生产。
4
SafetyuprvisonBh'mldcg,bwkqPC".F():TXJA12Izj
答案:
SafetyuprvisonBh'mldcg,bwkqPC".F():TXJA12Izj
基解:X⑴、X⑵、X⑷、X⑺,可行解:X⑴、X⑶、X⑹、X⑺,基可行解:X⑴、X⑺,非.基.可行解: X⑶、X⑹(或非.基可行解:X⑵、X⑶、X⑷、X⑸、X⑹)。 三、求解下列线性规划问题:
MinZ 5x1 4x2
或等于零,则可以判断其对偶问题具有无界解;(✓)
(9) 若线性规划问题中的 bi,cj 值同时发生变化,反映到最终单纯形表中,不会出现原问题与 对偶问题均为非可行解的情况;()
(10)在线性规划问题的最优解中,如某一变量 xj 为非基变量,则在原来问题中,无论改变它 在目标函数中的系数 cj 或在各约束中的相应系数 aij,反映到最终单纯形表中,除该列数字有 变化外,将不会引起其他列数字的变化。(✓)
第一章 L.P 及单纯形法练习题答案
一、判断下列说法是否正确
1. 线性规划模型中增加一个约束条件,可行域的范围一般将缩小,减少一个约束条件, 可行域的范围一般将扩大。(✓)
2. 线性规划问题的每一个基解对应可行域的一个顶点。() 3. 如线性规划问题存在某个最优解,则该最优解一定对应可行域边界上的一个点。(✓) 4. 单纯形法计算中,如不按最小比值原则选取换出变量,则在下一个基可行解中至少有
运筹学第一章线性规划及其单纯形法习

x6
x7
-M
-M
6 3 2 0 0 -1 0 1
2 3
Cj
比值
CB
XB
b
检验数j
x1 x2 x3 x4 x5 x6 x7
-2 -3 -1 0 0 -M -M
x2
x7
-3
-M
2 1/4 1 1/2 -1/4 0 1/4 0
2 5/2 0 -1 1/2 -1 -1/2 1
8 4/5
Cj
0.03
B1
6
8
4000
0.06
B2
4
11
7000
0.11
B3
7
4000
0.05
原料费
0.25
0.35
0.50
售价
1.25
2.00
2.80
设备
产品
设备有效台时
设备加工费
I
II
III
A1
5
10
6000
0.05
A2
7
9
12
10000
0.03
B1
6
8
4000
0.06
B2
4
11
7000
0.11
B3
7
4000
i=5, j=5, k=-3/2, l=0
01
02
综上所述:
设 是线性规划问题 的最优解。若目标函数中用 代替 C后,问题的最 优解变为
求证:
证明:因为
将(2)-(1)有
设备
产品
设备有效台时
设备加工费
I
II
1 3 第一章线性规划与单纯形法运筹学习题集第一章线性规划与单纯形

1 3 第一章线性规划与单纯形法运筹学习题集第一章线性规划与单纯形13第一章线性规划与单纯形法运筹学习题集第一章线性规划与单纯形法复习思考题1. 试述线性规划数学模型的结构及各要素的特征。
2. 求解线性规划问题时可能出现哪几种结果?哪些结果反映建模时有错误?3. 什么是线性规划问题的标准形式?如何将一个非标准型的线性规划问题转化为标准形式?4. 试述线性规划问题的可行解、基解、基可行解、最优解的概念以及上述解之间的相互关系。
5. 试述单纯形法的计算步骤,如何在单纯形表上判别问题是具有唯一最优解、无穷多最优解、无界解或无可行解?6. 如果线性规划的标准型变换为求目标函数的极小化min z,则用单纯形法计算时如何判别问题已得到最优解?7. 在确定初始可行基时,什么情况下要在约束条件中增添人工变量?在目标函数中人工变量前的系数为(-M)的经济意义是什么?8. 什么是单纯形法计算的两阶段法?为什么要将计算分成两个阶段进行,如何根据第一阶段的计算结果来判定第二阶段的计算是否需要继续进行?9. 简述退化的含义及处理退化的勃兰特规则。
10. 举例说明生产和生活中应用线性规划的可能案例,并对如何应用进行必要描述。
11. 判断下列说法是否正确:(a) 图解法同单纯形法虽然求解的形式不同,但从几何上理解,两者是一致的;(b) 线性规划模型中增加一个约束条件,可行域的范围一般将缩小,减少一个约束条件,可行域的范围一般将扩大;(c) 线性规划问题的每一个基解对应可行域的一个顶点;(d) 如线性规划问题存在可行域,则可行域一定包含坐标的原点;(e) 对取值无约束的变量xj,通常令xj=x′j-x″j,其中x′j?0,x″j?0,在用单纯形法求得的最优解中有可能同时出现x′j,0,x″j,0;(f) 用单纯形法求解标准型的线性规划问题时,与σj,0对应的变量都可以被选作换入变量; (g) 单纯形法计算中,如不按最小比值原则选取换出变量,则在下一个解中至少有一个基变量的值为负;(h) 单纯形法计算中,选取最大正检验数σk对应的变量xk作为换入变量,将使目标函数值得到最快的增长;(i) 一旦一个人工变量在迭代中变为非基变量后,则该变量及相应列的数字可以从单纯形表中删除,而不影响计算结果;(j) 线性规划问题的任一可行解都可以用全部基可行解的线性组合表示; (k)若X1,X2分别是某一线性规划问题的最优解,则X=λ1X1+λ2X2也是该线性规划问题的最优解,其中λ1、λ2可以为任意正的实数;(l) 线性规划用两阶段法求解时,第一阶段的目标函数通常写为minz=?ixai(xai为人工变量),但也可写为min z=?ikixai,只要所有ki均为大于零的常数;(m)对一个有n个变量、m个约束的标准型的线性规划问题,其可行域的顶点恰好为Cmn个; (n) 单纯形法的迭代计算过程是从一个可行解转换到目标函数值更大的另一个可行解; (o) 线性规划问题的可行解如为最优解,则该可行解一定是基可行解; (p) 若线性规划问题具有可行解,且其可行域有界,则该线性规划问题最多具有有限个数的最优解;(q) 线性规划可行域的某一顶点若其目标函数值优于相邻的所有顶点的目标函数值,则该顶点处的目标函数值达到最优;(r) 将线性规划约束条件的“?”号及“?”号变换成“=”号,将使问题的最优目标函数值得到改善;(s) 线性规划目标函数中系数最大的变量在最优解中总是取正的值;(t) 一个企业利用3种资源生产4种产品,建立线性规划模型求解得到的最优解中,最多只含有3种产品的组合;(u) 若线性规划问题的可行域可以伸展到无限,则该问题一定具有无界解; (v) 一个线性规划问题求解时的迭代工作量主要取决于变量数的多少,与约束条件的数量关系相对较小。
运筹学习题
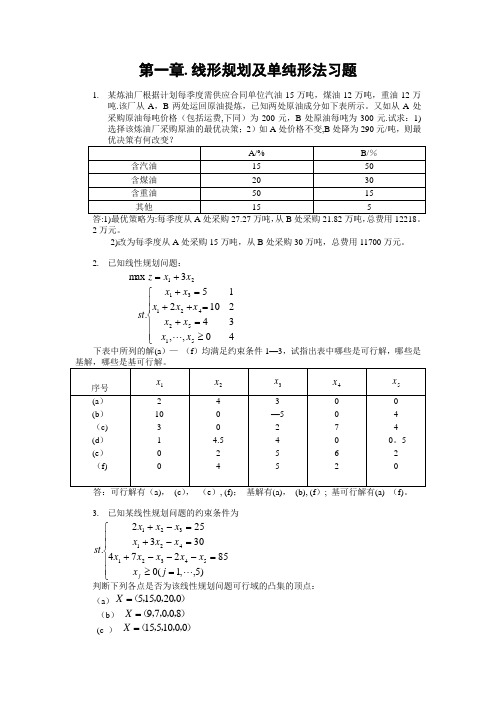
第一章. 线形规划及单纯形法习题1. 某炼油厂根据计划每季度需供应合同单位汽油15万吨,煤油12万吨,重油12万吨.该厂从A ,B 两处运回原油提炼,已知两处原油成分如下表所示。
又如从A 处采购原油每吨价格(包括运费,下同)为200元,B 处原油每吨为300元.试求:1)选择该炼油厂采购原油的最优决策;2)如A 处价格不变,B 处降为290元/吨,则最2万元。
2)改为每季度从A 处采购15万吨,从B 处采购30万吨,总费用11700万元。
2. 已知线性规划问题: 213m ax x x z +=⎪⎪⎩⎪⎪⎨⎧≥=+=++=+40,,34210215.515242131x x x x x x x x x st下表中所列的解(a )— (f )均满足约束条件1—3,试指出表中哪些是可行解,哪些是3. 已知某线性规划问题的约束条件为⎪⎪⎩⎪⎪⎨⎧=≥=---+=-+=-+)5,,1(0852********.54321421321 j x x x x x x x x x x x x st j判断下列各点是否为该线性规划问题可行域的凸集的顶点:(a )),,,,(0200155=X(b ) ),,,,(80079=X (c ) ),,,,(0010515=X答:该线性规划问题中⎪⎪⎪⎭⎫ ⎝⎛=4121p⎪⎪⎪⎭⎫ ⎝⎛=7312p⎪⎪⎪⎭⎫ ⎝⎛--=1013p ⎪⎪⎪⎭⎫ ⎝⎛--=2104p⎪⎪⎪⎭⎫ ⎝⎛-=1005p (a ) 因有0421=++-p p p ,故不是凸集顶点;(b ) (9,7,0,0,8)为非可行域的点(c ) 因321,,p p p 线性相关,故非凸集的顶点。
4. 在单纯形法迭代中,任何从基变量中替换出来的变量在紧接着的下一次迭代中会不会立即再进入基变量,为什么?答:不可能,因刚从基中被替换出来的变量在下一个单纯形表中,其检验数一定为负.5. 求解线性规划问题当某一变量jx 的取值无约束时,通常用'''j j jx x x -=来替换,其中0'≥j x ,0''≥j x 。
运筹学习题解答(chap1 线性规划及单纯形法)

第一章 线性规划及单纯形法一、写出下列线性规划的标准形式,用单纯形法求解,并指出其解属于哪种情况。
1、P55,1.3(a)21510m ax x x Z +=⎪⎩⎪⎨⎧≥≤+≤+0x ,x 8x 2x 59x 4x 3.t .s 212121 解:将模型化为标准型21510x x Z Max +=⎪⎩⎪⎨⎧≥=++=++0,,,825943..4321421321x x x x x x x x x x t s 单纯形表如下因所有检验数0j ≤σ,已达最优解,最优解是)2,1(*=X ,最优目标值为2。
由检验数的情况可知,该问题有唯一最优解。
2、 P55,1.3(b)21x x 2Z m ax +=s.t⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,524261552121212x x x x x x x解:将模型化为标准型21x x 2Z Max +=t s . ⎪⎪⎩⎪⎪⎨⎧≥=++=++=+0x ,...,x ,x ,5x x x ,24x x 2x 6,15x x 552152142132 单纯形表如下因所有检验数0j ≤σ,已达最优解,最优解是)0,0,2,2,2(X *=,最有目标值为217。
由检验数的情况可知,该问题有唯一最优解。
3、3212x x x Z Min -+=,t s . ⎪⎪⎩⎪⎪⎨⎧≥≤++≤+-≤-+0,,,5,822,422321321321321x x x x x x x x x x x x 解:将模型化为标准型:3212x x x Z Min -+=t s . ⎪⎪⎩⎪⎪⎨⎧≥=+++=++-=+-+0,,,5,822,422321632153214321x x x x x x x x x x x x x x x 用单纯形法迭代最优解为(0,0,4),最优值为-4。
4、43213x x x x Z Min +++=t s . ⎪⎪⎩⎪⎪⎨⎧≥=++=++-0,,,,,63,4224321421321x x x x x x x x x x 解:因为所有检验数均已非负,故已是最优解,最优解为(0,2,0,4),--10分最优目标值:6Z =*。
运筹学习题

习题一1.1 用图解法求解下列线性规划问题,并指出各问题是具有唯一最优解、无穷多最优解、无界解或无可行解。
(1) min z =6x1+4x2(2) max z =4x1+8x2st. 2x1+x2≥1 st. 2x1+2x2≤103x1+4x2≥1.5 -x1+x2≥8x1, x2≥0 x1, x2≥0(3) max z =x1+x2(4) max z =3x1-2x2st. 8x1+6x2≥24 st. x1+x2≤14x1+6x2≥-12 2x1+2x2≥42x2≥4 x1, x2≥0x1, x2≥0(5) max z =3x1+9x2(6) max z =3x1+4x2st. x1+3x2≤22 st. -x1+2x2≤8-x1+x2≤4 x1+2x2≤12x2≤6 2x1+x2≤162x1-5x2≤0 x1, x2≥0x1, x2≥01.2. 在下列线性规划问题中,找出所有基本解,指出哪些是基本可行解并分别代入目标函数,比较找出最优解。
(1) max z =3x1+5x2(2) min z =4x1+12x2+18x3st. x1+x3=4 st. x1+3x3-x4=32x2+x4=12 2x2+2x3-x5=53x1+2x2+x5=18 x j≥0 (j=1, (5)x j≥0 (j=1, (5)1.3. 分别用图解法和单纯形法求解下列线性规划问题,并对照指出单纯形法迭代的每一步相当于图解法可行域中的哪一个顶点。
(1) max z =10x1+5x2st. 3x1+4x2≤95x1+2x2≤8x1, x2≥0(2) max z =100x1+200x2st. x1+x2≤500x1≤2002x1+6x2≤1200x1, x2≥01.4. 分别用大M法和两阶段法求解下列线性规划问题,并指出问题的解属于哪一类:(1) max z =4x1+5x2+x3(2) max z =2x1+x2+x3st. 3x1+2x2+x3≥18 st. 4x1+2x2+2x3≥42x1+x2≤4 2x1+4x2≤20x1+x2-x3=5 4x1+8x2+2x3≤16x j≥0 (j=1,2,3)x j≥0 (j=1,2,3)(3) max z = x 1+ x 2 (4) max z =x 1+2x 2+3x 3-x 4 st. 8x 1+6x 2≥24 st. x 1+2x 2+3x 3=154x 1+6x 2≥-12 2x 1+ x 2+5x 3=202x 2≥4 x 1+2x 2+ x 3+ x 4=10x 1, x 2≥0 x j ≥0 (j =1, (4)(5) max z =4x 1+6x 2 (6) max z =5x 1+3x 2+6x 3 st. 2x 1+4x 2 ≤180 st. x 1+2x 2+ x 3≤183x 1+2x 2 ≤150 2x 1+ x 2+3x 3≤16 x 1+ x 2=57 x 1+ x 2+ x 3=10x 2≥22 x 1, x 2≥0,x 3无约束 x 1, x 2≥01.5 线性规划问题max z =CX ,AX =b ,X ≥0,如X*是该问题的最优解,又λ>0为某一常数,分别讨论下列情况时最优解的变化:(1) 目标函数变为max z =λCX ;(2) 目标函数变为max z =(C +λ)X ;(3) 目标函数变为max z =C X ,约束条件变为AX =λb 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
√ √ √ √ √ √
基解
√ √ √ √ √ √
是否为基可行解
(-4, 11/2, 0 , 0) (2/5, 0, 11/5 , 0) (-1/3, 0, 0, 11/6) (0, 1/2, 2, 0) (0, -1/2, 0, 2) (0, 0, 1, 1)
×
√
×
√
×
√
4、已知线性规划问题 :
max Z x1 3x2 x1 x 2 x 1 2 st. x2 x1 ... x3 x4 x5 x5 0 5 10 4
检验数j
Cj CB -3 -M XB x2 2
-2
-3
x2 1
-1
0
0
x5
-M
x6 1/4
3 3 M 2 4
-M
x7 0
b
2
2M 6
x1 1/4
x3 x4
比 值 8
1/2 -1/4 0
x7
5/2
5 5 M 2 4
0
0
-1
M 1 2
1/2 -1 -1/2
M 3 2 4 M
-2
-3 x2 4Leabharlann -100 x5 0
-M x6 1
-M x7 0
b
6
0
x1 1
x3 x4 2 -1
比 值
3
-2
2
-3
0
-1
0
0
-1
0
0
1
检验数j
-M -M
Cj CB -M -M XB x6 x7 8 6
-2
-3 x2 4 2
-1
0
0 x5 0 -1
-M x6 1 0
0
-M x7 0 1
0
b
x1 1 3
min Z 5 x1 2 x2 3x3 2 x4 x1 2 x2 3x3 4 x4 7 s.t. 2 x1 2 x2 x3 2 x4 3 x 0( j 1,...., 4) j
关键:判断2个列向量线性相关性,若线性无关,则成为基
无穷多最优解
max Z x1 x 2 6 x1 10 x 2 120 s.t. 5 x1 10 3 x2 8
X*=(10, 6) 唯一解
max Z 5 x1 6 x 2 2 x1 x 2 2 s.t. 2 x1 3x 2 2 x1, x 2 0
课后练习(二)
1、分别用图解法和单纯形法求解下述线性规划问题,并 指出单纯形法迭代的每一步相当于图解法可行域中的哪一 个顶点
max Z 10 x1 5 x2 3 x1 4 x2 9 st. 5 x1 2 x2 8 x ,x 0 1 2
max Z 2 x1 x2 5 x2 15 6 x 2 x 24 1 2 st. x1 x2 5 x1 , x2 0
max Z 6 x1 2 x2 10 x3 8 x4 6 x2 4 x3 4 x4 20 5 x1 3x 3x2 2 x3 8 x4 25 1 st. 2 x2 x3 3x4 10 4 x1 x j 0 ( j 1, 2,3, 4)
1
0
4/5
检验数j
Cj
CB -3 -2 XB x2 x1
-2
-3
-1
0
0
-M
-M
b
9/5
x1
0
x2
1
x3 x4
x5
x6
x7
比 值
3/5 -3/10 1/10 3/10 -1/10
4/5
7
1
0
0
0
-2/5 1/5 -2/5 -1/5 2/5
0 1 2 1 1 1 M M 2 2 2
Cj CB 0 0 XB x3 x4
b
9 8 0 21/5 8/5
10 x1 3 5 10 0 1
5 x2 4 2 5 14/5 2/5
0 x3 1 0 0 1 0
0 x4 0 1 0 -3/5 1/5
比 值
9/3=3 8/5
检验数j 0 x3
3/2 4
10
x1
检验数j -80/5
5 10 x2 x1 3/2 1
2 1 0 1 3 0 4 7 1
X (9, 7, 0, 0, 0)
2 1 1 0 0 A 1 3 0 1 0 4 7 1 2 1
2 1 1 1 3 0 X (15,5,10, 0, 0) 不是基,故 4 7 1 不是基解,更不可能是基可行解
Cj CB 0 0 0 XB x4 b 60 10 20
2
x1 3 1 1
-1
x2 1 -1 1
1
x3 1 2 -1
0
x4 1 0 0
0
x5 0 1 0
0
x6 0 0 1
比 值
60/3=20
x5
x6
10/1=10
20/1=20
检验数j
0 2 0 x4 x1 x6
0
30 10
2
0 1
-1
4 -1
1
1
2 3 4
下表中所列的解均满足约束条件1-3,试指出表中哪些是可行 解,哪些是基解,哪些是基可行解。
序号 A X1 2 X2 4 X3 3 X4 0 X5 0
B
C D E F
10
3 1 0 0
0
0 4.5 2 4
-5
2 4 5 5
0
7 0 6 2
4
4 -0.5 2 0
可行解有(a), (c), (e), (f); p1 p2 p3 p4 p5
0 1 0
1
0 0 1
-3
1 1/2 -3/2
0
1 0 0
-2
-1 1/2 -1/2
0
-2 1/2 1/2
x1
x2
检验数j
-25
0
0
-3/2
0
-3/2
-1/2
同理: (2)为无界解
3 用单纯形法中的大M法求解下列线性规划问题,并指出属 那一类解
min Z 2 x1 3 x2 x3 x1 st. 3 x1 x , 1 4 x2 2 x2 x2 , 2 x3 x3 0 8 6
课后练习(一)
1 用图解法求下列线性规划问题,并指出问题具有唯一 最优解、无穷多最优解、无界界还是无可行解。
max Z 3 x1 2 x 2 2 x1 x 2 2 s.t. 3 x1 4 x 2 12 x1, x 2 0 无可行解
min Z 2 x1 3 x 2 4 x1 6 x 2 6 s.t 4 x1 2 x 2 4 x1, x 2 0
1 2 3 4 A 2 2 1 2
p1 p2 p3 p4
1 2 3 4 A 2 2 1 2
序号 1 2 3 4 5 6 序号 1 2 3 4 5 6 向量组 p1 p2 p1 p3 p1 p4 p2 p3 p2 p4 p3 p4 基 p1 p1 p1 p2 p2 p3 p2 p3 p4 p3 p4 p4 是否线性无关 是否为基
x3 x4 2 -1 0 0
比 值
检验数j
14M 4M-2 6M-3 2M-1 -M -M
Cj CB -M -M XB
-2
-3 x2
4 2
-1
0
0 x5
0 -1
-M x6
1 0
0
-M x7
0 1
0
b
8 6
x1
1 3
x3 x4
2 -1 0 0
比 值 2
x6 x7
3
检验数j
14M 4M-2 6M-3 2M-1 -M -M
化为标准式有
max Z 2 x1 3 x2 x3 0 x4 0 x5 Mx6 Mx7 4 x2 x1 st. 3x1 2 x2 x 0 1~7 2 x3 x4 x5 x6 x7 8 6
Cj
CB -M -M XB x6 x7 8
X3 X1
2 a
Cj-Zj
(1)a~g的值
X1 c d b
X2 0 e -1
X3 1 0 f
x4 1/5 1 g
(2) 表中给出的解是否为最优解
因为目标函数值为10,而Z=5x1+3x2,由单纯形表可知 x1=a, x2=0, 故a = 2 因为x1、x2为基变量,所以因当满足高斯消元的形式 (proper form from Gaussian elimination), 故c=0, d=1, b=0; f=0 由检验数的定义可知: j c j -1=3 -(0×0 +e×5)
检验数j
4、求解线性规划问题当某一变量的取值无约束时,通 常用 x j
x x
' j
'' j
来替换,其中
。 x'j 0 ,x''j 0
试说明,能否在基变量中同时出现,为什么?
不可能。因为 P P
' j
'' j
故
P P 0
' j '' j
5、 下表为用单纯形法计算时某一步的表格。已知该线 性规划的目标函数为 max Z 5x1 3x2约束形式为 x3、x4为松弛变量,表中解代入目标函数后得Z=10
无界解
