过程能力分析报告(图表)
过程能力分析minitab版

过程能力分析minitab版过程能力概述(Process Capability Overview)在过程处于统计控制状态之后,即生产比较稳定时,你很可能希望知道过程能力,也即满足规格界限和生产良品的能力。
你可以将过程变差的宽度与规格界限的差距进行对比来片段过程能力。
在评价其能力之前,过程应该处于控制状态,否则,你得出的过程能力的估计是不正确的。
你可以画能力条形图和能力点图来评价过程能力,这些图形可以帮助你评价数据的分布并验证过程是否受控。
你还可以计算过程指数,即规范公差与自然过程变差的比值。
过程指数是评价过程能力的一个简单方法。
因为它们无单位,你可以用能力统计量来比较不同的过程。
一、选择能力命令(Choosing a capability command)Minitab提供了许多不同的能力分析命令,你可以根据数据的属性及其分布来选择适当的命令。
你可以为以下几个方面进行能力分析:正态或Weibull概率模型(适合于测量数据)很可能来源于具有明显组间变差的总体的正态数据二项分布或泊松概率分布模型(适合于属性数据或计数数据)注:如果你的数据倾斜严重,你可以利用Box-Cox转换或使用Weibull 概率模型。
在进行能力分析时,选择正确的分布是必要的。
例如:Minitab 提供基于正态和Weibull概率模型的能力分析。
使用正态概率模型的命令提供更完整的一系列的统计量,但是你的数据必须近似服从正态分布以保证统计量适合于这些数据。
举例来说,Analysis (Normal) 利用正态概率模型来估计期望的PPM。
这些统计量的结实依赖于两个假设:数据来自于稳定的过程,且近似服从的正态分布。
类似地,Capability Analysis (Weibull) 利用Weibull 分布模型计算PPM。
在两种情况下,统计的有效性依赖于假设的分布的有效性。
如果数据倾斜严重,基于正态分布的概率会提供对实际的超出规格的概率做比较差的统计。
工序(过程)能力分析报告PPT课件( 39页)

27.05.2019
5
什么是工序能力指数
工序能力指数是衡量工序能力对产品规格要
求满足程度的数量值,记为Cp。通常以规格范围T
与工序能力B的比值来表示。即:
Cp
T B
T 6S
其中T=规格上限TU - 规格下限TL
x27.05.2019
6
工序能力与工序能力指数的区别
工序能力是工序的实际加工能力,而工序能 力指数是指工序能力对规格要求的满足程度。
2.20
2.30
2.40
2.50
2.60
2.70
2.80
27.05.2019
0.04 13.34 7.26 3.64 1.69 0.73 0.29 0.11 0.04 0.01 0.00
0.08 13.64 7.48 3.83 1.89 0.83 0.35 0.14 0.05 0.02 0.01
0.12 13.99 7.85 4.16 2.09 1.00 0.45 0.20 0.08 0.03 0.01 0.00
工序处于标准状态,是指设备、材料、工艺、环境、 测量均处于标准作业条件,人员的操作也是正确的。
工序的实际加工能力是指工序质量特性的分散(或波
动)有多大。以3σ原则这样的分散范围表示工序能力
既能保证产品的质量要求,又能具有较好的经济性。
工序能力:B=6σ 或 B≈6S
27.05.2019
4
谁影响工序能力
C
p
2 3
0 . 48 0 . 48
0 . 734
27.05.2019
22
工序能力的评价与处置
1 计件值 2 计点值
27.05.2019
过程能力SPC图表
15.0 155.00 155.00 155.00 155.00 155.00 155.00 155.00 155.50 155.00 155.00 156.00 155.00 155.00 155.00 155.00 155.00 155.00 156.00 155.00 156.00 156.00 156.00 155.00 155.00
UCLX X A2 R CLX X LCLX X A2 R UCL R D4 R CLR R LCLR D3 R
0.42 90.6
USL
SL
90.6
LSL
90.6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
R管制圖
0.03
0.02
Ca ( X SL) T
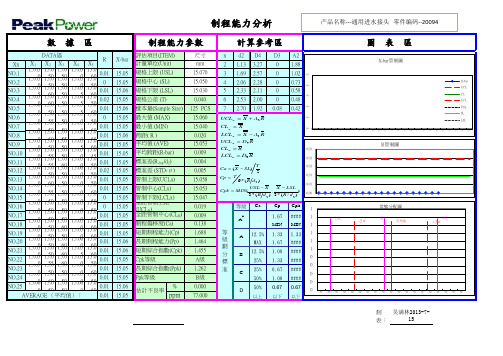
制程能力分析
产品名称---通用进水接头 零件编码--20094
數 據 區
制程能力參數
DATA區
R
Xn X1 X2 X3 X4 X5
NO.1 NO.2 NO.3 NO.4 NO.5 NO.6 NO.7 NO.8 NO.9 NO.10 NO.11 NO.12 NO.13 NO.14 NO.15 NO.16 NO.17 NO.18 NO.19 NO.20 NO.21 NO.22 NO.23 NO.24 NO.25
0
15.0 155.00 155.00 156.00 156.00 155.00 155.05 155.00 156.00 155.00 155.05 155.05 155.00 156.00 155.05 155.00 155.00 155.00 155.00 155.00 155.00 155.00 155.05 155.00 156.00
过程能力分析minitab版

过程能力概述(Process CapabilityOverview)在过程处于统计控制状态之后,即生产比较稳定时,你很可能希望知道过程能力,也即满足规格界限和生产良品的能力。
你可以将过程变差的宽度与规格界限的差距进行对比来片段过程能力。
在评价其能力之前,过程应该处于控制状态,否则,你得出的过程能力的估计是不正确的。
你可以画能力条形图和能力点图来评价过程能力,这些图形可以帮助你评价数据的分布并验证过程是否受控。
你还可以计算过程指数,即规范公差与自然过程变差的比值。
过程指数是评价过程能力的一个简单方法。
因为它们无单位,你可以用能力统计量来比较不同的过程。
一、选择能力命令(Choosing a capability command)Minitab提供了许多不同的能力分析命令,你可以根据数据的属性及其分布来选择适当的命令。
你可以为以下几个方面进行能力分析:⏹正态或Weibull概率模型(适合于测量数据)⏹很可能来源于具有明显组间变差的总体的正态数据⏹二项分布或泊松概率分布模型(适合于属性数据或计数数据)注:如果你的数据倾斜严重,你可以利用Box-Cox转换或使用Weibull 概率模型。
在进行能力分析时,选择正确的分布是必要的。
例如:Minitab提供基于正态和Weibull概率模型的能力分析。
使用正态概率模型的命令提供更完整的一系列的统计量,但是你的数据必须近似服从正态分布以保证统计量适合于这些数据。
举例来说,Analysis (Normal) 利用正态概率模型来估计期望的PPM。
这些统计量的结实依赖于两个假设:数据来自于稳定的过程,且近似服从的正态分布。
类似地,Capability Analysis (Weibull) 利用Weibull 分布模型计算PPM。
在两种情况下,统计的有效性依赖于假设的分布的有效性。
如果数据倾斜严重,基于正态分布的概率会提供对实际的超出规格的概率做比较差的统计。
这种情况下,转化数据使其更近似于正态分布,或为数据选择不同的概率模型。
过程能力分析报告(图表)

100 80
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24
25
R控制图
1.00 0.80 0.60 0.40 0.20 0.00
NO.10 ###### NO.11 190.00 NO.12 190.00 NO.13 198.00 NO.14 197.00 NO.15 193.00 NO.16 198.00 NO.17 197.00 NO.18 195.00 NO.19 192.00 NO.20 195.00 NO.21 197.00 NO.22 198.00 NO.23 195.00 NO.24 196.00 NO.25 198.00 AVERAGE (平均值):
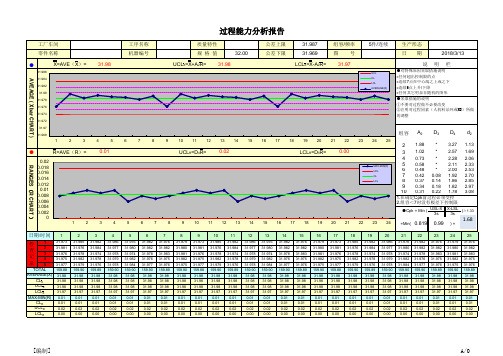
过程能力分析报告
数据输入区域
DATA区 Xn NO.1 NO.2 NO.3 NO.4 NO.5 NO.6 NO.7 NO.8 NO.9 X1
195.00 193.00 200.50 197.00 194.90
过程能力参数
R X-bar 评估項目(ITEM) 计量单位(Unit) 規格上限 (USL) 規格中心 (SL) 規格下限 (LSL) 規格公差 (T) 样本量(Sample Size) 最大值 (MAX) 最小值 (MIN) 跨距( R ) 平均值 (AVE) 平均跨距(R-bar) 标准差(R-bar/d2) 标准差 (STD-σ) 控制上限(UCLx) 控制中心(CLx) 控制下限(LCLx) 全距控制上限(UCLR) 全距控制中心(CLR) 过程偏移度(Ca) 短期过程能力(Cp) 长期过程能力(Pp) 0 0 0 0 0 197.00 198.00 195.00 196.00 198.00 短期綜合指数(Cpk) Cpk等級 长期綜合指数(Ppk) Ppk等級 估计不良率 % 2.13 A+級 0.00% 0.00 2.22 錫爐溫度 ℃ 215 100 180 35 25 PCS 200.5 190 10.5 196.80 0.00 #N/A 2.62 #N/A 196.80 #N/A #N/A 0.00 553.14% n 2 3 4 5 6 7
过程能力分析

目一、波动的概念录二、连续数据过程能力分析 三 离散数据过程能力分析 三、离散数据过程能力分析测量阶段1第 部分 第一部分 波动的概念测量阶段2波动的分类与原因通常,过程包含随机波动(由于一般或普遍原因造成的) 和非随机波动(由于特殊原因造成的)。
非随机波动随机波动 历史水平(μ0) 在 μ0 (±3σ0) 范围内的随机波动 不合 合格产品率 率 最佳水平(μ1) 在 μ1 (±3σ1) 范围内的随机波动 随机波动 时间 测量阶段3随机波动普遍原因Sa ample CountNP Chart for C18 7 6 5 4 3 2 1 0 0 5 10 15 20 25 LCL=0 NP=2.792 UCL=7.769¾过程波动随时间推移是稳定 的,可预测的。
¾处于控制状态。
处于控制状态 ¾原因: 固有的或是自然的。
Sample Number例: 垂直向上空(先把硬币垂直夹住) 抛掷 抛掷一枚硬币 枚硬币,统计硬币落 统计硬币落 地后每一面向上的次数。
当抛掷次数很多时,每面向上的次数大约 各占 半 只有微小差异 各占一半,只有微小差异。
差异原因:有风,每次抛掷动作有微小差异,地面不平整,等等。
测量阶段4非随机波动特殊原因Sample Count SC Chart for C110 1 UCL=9.719¾过程波动无法预测,处于失控 状态。
¾原因:工作标准不统一、不同 原因 工作标准不统 不同 操作者的技能、设备参数设置 不当。
¾目标:检测和消除特殊原因。
5 C=3.840 0 5 10 15 20 25LCL=0Sample Number例: 同样是抛硬币,抛1000次,AB两面各自向上的次数却相 同样是抛硬币 抛1000次 AB两面各自向上的次数却相 差400多次。
差异原因 操作者每次抛掷时 总时将硬币平放 差异原因:操作者每次抛掷时,总时将硬币平放,且总是将 总是将 正面朝上,然后抛出。
过程能力分析报告
0.01
0.01
0.02
0.02
0.00
0.00
1.68
10
31.985 31.976 31.978 31.982 31.979 159.90 31.98 31.98 31.98 31.97
0.01 0.01 0.02 0.00
11
31.982 31.984 31.974 31.978 31.976 159.89 31.98 31.98 31.98 31.97
0.02 0.018 0.016 0.014 0.012
0.01 0.008 0.006 0.004 0.002
0
4 0.73 * 2.28 2.06
MAX-MIN(R) UCL CL
5 0.58 * 2.11 2.33 6 0.48 * 2.00 2.53 7 0.42 0.08 1.92 2.70
2
31.985 31.976 31.978 31.982 31.979 159.90 31.98 31.98 31.98 31.97
0.01 0.01 0.02 0.00
3
31.982 31.984 31.974 31.978 31.976 159.89 31.98 31.98 31.98 31.97
0.01 0.01 0.02 0.00
24
31.979 31.980 31.981 31.982 31.975 159.90 31.98 31.98 31.98 31.97
0.01 0.01 0.02 0.00
25
31.976 31.982 31.983 31.975 31.976 159.89 31.98 31.98 31.98 31.97
0.01 0.01 0.02 0.00
CPK过程能力分析报告

17
9.75 9.76 9.75 9.77 9.75 48.78 9.76 9.75 9.76 9.74 0.02 0.02 0.04 0.00
18
9.74 9.74 9.75 9.76 9.75 48.74 9.75 9.75 9.76 9.74 0.02 0.02 0.04 0.00
19
9.75 9.76 9.75 9.76 9.75 48.77 9.75 9.75 9.76 9.74 0.01 0.02 0.04 0.00
过程能力分析报告
AVEAGE ( Xbar CHART )
工厂车间 零件名称
湘联 BYDLK-6203138 压块
螺母
●
X=AVE(X)=
9.75
工序名称 机器编号
9.77
9.765
9.76
9.755
9.75
9.745
9.74
9.735
9.73
9.725
1
2
3
4
5
6
7
8
成品 XL-PF-021
质量特性 规格值
[编制]
A/0
结论:
该过 程的 过程 能力
Cpk 为:
制表/日期:
审核/日期:
该过 程目 前能 被接 受, 批准 后即 1.68 可开 始生 产, 并按 照控 制计 划进 行。批准/日期:来自项目编号:[编制]
A/0
正方形 9.80
UCLX=X+A2R=
9.76
9 10 11 12 13 14 15
公差上限 公差下限
9.80
组容/频率
9.60
图号
LCLX=X-A2R=
9.74
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-10
0
-3σ
10
20
30
0.2 USL 0. 准
1
1
平均值 +3σ
A B C D
12.5% 1.33 MAX 25% 25% 50% 50%
以上
1.67 1.33 0.67 1.00 0.67
以下
0.12 0.1
12.5% 1.00
0 0 0
0.08 0.06 0.04 0.02 0
X2
X3
X4
X5
X-bar UCL CL LCL USL SL LSL
140 120
###### ###### ###### ######
UCLX X A2 R
CLX X LCLX X A2 R UCLR D4 R CLR R LCLR D3 R
T Ca ( X SL ) 2 Cp T 6 * (R d 2 )
过程能力分析报告
数据输入区域
DATA区 Xn NO.1 NO.2 NO.3 NO.4 NO.5 NO.6 NO.7 NO.8 NO.9 X1
195.00 193.00 200.50 197.00 194.90
过程能力参数
R X-bar 评估項目(ITEM) 计量单位(Unit) 規格上限 (USL) 規格中心 (SL) 規格下限 (LSL) 規格公差 (T) 样本量(Sample Size) 最大值 (MAX) 最小值 (MIN) 跨距( R ) 平均值 (AVE) 平均跨距(R-bar) 标准差(R-bar/d2) 标准差 (STD-σ) 控制上限(UCLx) 控制中心(CLx) 控制下限(LCLx) 全距控制上限(UCLR) 全距控制中心(CLR) 过程偏移度(Ca) 短期过程能力(Cp) 长期过程能力(Pp) 0 0 0 0 0 197.00 198.00 195.00 196.00 198.00 短期綜合指数(Cpk) Cpk等級 长期綜合指数(Ppk) Ppk等級 估计不良率 % 2.13 A+級 0.00% 0.00 2.22 錫爐溫度 ℃ 215 100 180 35 25 PCS 200.5 190 10.5 196.80 0.00 #N/A 2.62 #N/A 196.80 #N/A #N/A 0.00 553.14% n 2 3 4 5 6 7
100 80
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24
25
R控制图
1.00 0.80 0.60 0.40 0.20 0.00
NO.10 ###### NO.11 190.00 NO.12 190.00 NO.13 198.00 NO.14 197.00 NO.15 193.00 NO.16 198.00 NO.17 197.00 NO.18 195.00 NO.19 192.00 NO.20 195.00 NO.21 197.00 NO.22 198.00 NO.23 195.00 NO.24 196.00 NO.25 198.00 AVERAGE (平均值):
0.00 196.80 主管:
ppm
制表:
Cpk MIN (
USL X X LSL , ) 3 * (R d 2 ) 3 * (R / d 2 )
等級 A
+
Ca
Cp 1.67 MIN
Cpk 1.67 MIN 1.33 1.67 1.00 1.33 0.67 1.00 0.67
以下
-70
-60
-50
-40
-30
1
SL
正态分布图
-20
计算参考区
d2 1.13 1.69 2.06 2.33 2.53 2.70 D4 3.27 2.57 2.28 2.11 2.00 1.92 D3 0 0 0 0 0 0.08 A2 1.88 1.02 0.73 0.58 0.48 0.42
240 220 200 180
160
图 表 区
X-bar控制图
