CPK过程能力分析报告
过程能力与过程能力指数分析

过程能力与过程能力指数过程能力过程能力以往也称为工序能力。
过程能力是指过程加工质量方面的能力,它是衡量过程加工内在一致性的,是稳态下的最小波动。
而生产能力则是指加工数量方面的能力,二者不可混淆。
过程能力决定于质量因素,而与公差无关。
当过程处于稳态时,产品的计量质量特性值有99.73%落在μ±3σ的范围内,其中μ为质量特性值的总体均值,σ为质量特性值的总体标准差,也即有99.73%的产品落在上述6σ范围内,这几乎包括了全部产品。
故通常用6倍标准差(6σ)表示过程能力,它的数值越小越好。
过程能力指数(一)双侧公差情况的过程能力指数对于双侧公差情况,过程能力指数C p的定义为:C p= T =TU-TL (公式1);6σ 6σ式中,T为技术公差的幅度,T U、T L分别为上、下公差限,σ为质量特性值分布的总体标准差。
当σ 未知时,可用σˆ1=R/d2或σˆ2=s/c4估计,其中R为样本极差,R为其平均值,s占为样本标准差,s为其平均值,d2、c4为修偏系数,可查国标《常规控制图》GB/T4091—2001表。
注意,估计必须在稳态下进行,这点在国标GB/T4091—2001《常规控制图》中有明确的规定并再三强调,不可忽视。
在过程能力指数计算公式中,T反映对产品的技术要求,而σ反映过程加工的一致性,所以在过程能力指数C p中将6σ与T比较,就反映了过程加工质量满足产品技术要求的程度。
根据T与6σ的相对大小可以得到过程能力指数C p。
如下图的三种典型情况。
C p值越大,表明加工质量越高,但这时对设备和操作人员的要求也高,加工成本也越大,所以对于C p值的选择应根据技术与经济的综合分析来决定。
当T=6σ,C p=1,从表面上看,似乎这是既满足技术要求又很经济的情况。
但由于过程总是波动的,分布中心一有偏移,不合格品率就要增加,因此,通常应取C p大于1。
各种分布情况下的C p值一般,对于过程能力指数制定了如下表所示的评价参考。
CPK过程能力分析18
45
40
22
87
0.7040
2.0590
-0.1997
0.1997 0.0000 -0.1997 #DIV/0! 0.2533 0.2523 0.0642 0.0637 0.0000 #DIV/0! -0.2695
40
35 31
30
Frequency
25
22
20
16
16
15
10
5
0
2
52.60 51.80 51.80 52.40 52.40 52.00 52.20 52.40 52.40 51.80 52.20 51.80 52.20 52.20 52.40 51.80 51.80 51.80 52.20 52.00 52.60 52.40 52.20 51.80 52.20
零件号
nTuomolber
图纸号
nDuemscbreiprti
模 可具 以类 不型 用
on
填写
SLwPrEC
52.000
Spec
52.000
53.000
PNLOUMSINA L
Part
Dept:
dEensgc. ripti
QA 产品名称
c#hg.
Cavities
Units
0.000
MUpINr US
52.000
Spec
Average (X chart)
0.000 52.000
SignifPicaRntO C E S S
trends of RUN
Increasing LHEONWGTH
MRUANNY
Decreasing LHEONWGTH
设备cpk的报告

设备CPK的报告1. 简介设备CPK是一种用于衡量设备性能稳定性的统计指标。
CPK值越高,表示设备的稳定性越好,能够更可靠地满足产品质量要求。
本文将介绍设备CPK的计算方法、解读及其在质量管理中的应用。
2. 设备CPK的计算方法设备CPK的计算方法涉及到设备的测量数据和产品规格。
以下是计算CPK值的步骤:步骤1:收集数据首先,需要收集设备的测量数据,例如长度、直径、重量等。
数据应来自设备正常运行状态下的多个样本。
步骤2:计算平均值和标准差根据收集到的数据,计算平均值和标准差。
平均值表示设备的测量结果的中心位置,标准差表示测量结果的离散程度。
步骤3:计算规格上限和下限根据产品规格,确定设备测量结果的规格上限和下限。
规格上限表示产品所允许的最大值,规格下限表示产品所允许的最小值。
步骤4:计算过程能力指数使用以下公式计算设备的过程能力指数(CPK): CPK = min((规格上限 - 平均值) / (3 * 标准差), (平均值 - 规格下限) / (3 * 标准差))步骤5:解读CPK值CPK值介于0和1之间。
CPK值越接近1,表示设备的过程能力越好,能够更好地控制产品的质量;CPK值越接近0,表示设备的过程能力越差,产品质量可能无法满足规格要求。
3. 设备CPK的应用设备CPK在质量管理中有广泛的应用。
以下是一些常见的应用场景:质量控制通过监测设备CPK值的变化,可以及时发现设备性能的变化,从而采取适当的措施来调整设备,以保持稳定的过程能力。
这有助于提高产品质量,减少不良品率。
设备比较通过比较不同设备的CPK值,可以评估设备之间的性能差异。
这有助于选择最适合生产要求的设备,并进行相应的优化。
故障分析当产品出现质量问题时,通过分析设备CPK值的变化,可以确定设备是否存在故障或异常。
这有助于快速定位问题,并采取纠正措施,以避免类似问题再次发生。
4. 注意事项在使用设备CPK进行质量管理时,需要注意以下事项:样本选择在收集数据时,应确保样本的代表性,以避免采集到偏离正常状态的数据,导致CPK值的不准确。
CPK(过程能力分析报告方法)

过程能力分析过程能力也称工序能力,是指过程加工方面满足加工质量的能力,它是衡量过程加工内在一致性的,最稳态下的最小波动。
当过程处于稳态时,产品的质量特性值有99.73%散布在区间[μ-3σ,μ+3σ],(其中μ为产品特性值的总体均值,σ为产品特性值总体标准差)也即几乎全部产品特性值都落在6σ的范围内﹔因此,通常用6σ表示过程能力,它的值越小越好。
为什么要进行过程能力分析进行过程能力分析,实质上就是通过系统地分析和研究来评定过程能力与指定需求的一致性。
之所以要进行过程能力分析,有两个主要原因。
首先,我们需要知道过程度量所能够提供的基线在数量上的受控性;其次,由于我们的度量计划还相当"不成熟",因此需要对过程度量基线进行评估,来决定是否对其进行改动以反映过程能力的改进情况。
根据过程能力的数量指标,我们可以相应地放宽或缩小基线的控制条件。
工序过程能力分析工序过程能力指该工序过程在5M1E正常的状态下,能稳定地生产合格品的实际加工能力。
过程能力取决于机器设备、材料、工艺、工艺装备的精度、工人的工作质量以及其他技术条件。
过程能力指数用Cp 、Cpk表示。
非正态数据的过程能力分析方法当需要进行过程能力分析的计量数据呈非正态分布时,直接按普通的计数数据过程能力分析的方法处理会有很大的风险。
一般解决方案的原则有两大类:一类是设法将非正态数据转换成正态数据,然后就可按正态数据的计算方法进行分析;另一类是根据以非参数统计方法为基础,推导出一套新的计算方法进行分析。
遵循这两大类原则,在实际工作中成熟的实现方法主要有三种,现在简要介绍每种方法的操作步骤。
非正态数据的过程能力分析方法1:Box-Cox变换法非正态数据的过程能力分析方法2:Johnson变换法非正态数据的过程能力分析方法3:非参数计算法当第一种、第二种方法无法适用,即均无法找到合适的转换方法时,还有第三种方法可供尝试,即以非参数方法为基数,不需对原始数据做任何转换,直接按以下数学公式就可进行过程能力指数CP和CPK的计算和分析。
CPK统计分析范文

CPK统计分析范文CPK是指过程能力指数(Process Capability Index),它反映了过程的稳定性和可控性。
计算CPK需要知道过程的规格范围和实际数据,通过分析数据的分布情况,确定过程在规格范围内的能力。
CPK分析通过计算过程的上限规格指数(Upper Specification Index,USL),下限规格指数(Lower Specification Index,LSL),过程均值(Process Mean,μ)和过程标准差(Process Standard Deviation,σ),来评估过程的能力。
CPK的计算公式为:CPK = min((USL-μ)/(3σ), (μ-LSL)/(3σ))CPK值是以1为中心点的一个指标,当CPK=1时,说明过程范围与规格范围基本一致;当CPK>1时,说明过程范围比规格范围更加宽松;当CPK<1时,说明过程范围比规格范围更加严格。
CPK分析通常分为两个步骤:数据收集和数据分析。
在数据收集阶段,需要收集关于过程的实际数据,并记录下来。
这些数据可以是过程中的样本数据或者连续数据。
在数据分析阶段,需要使用统计工具来分析数据的分布情况。
常用的统计工具包括直方图、正态概率图和盒须图等。
直方图可以帮助我们了解数据的分布情况,显示数据的频率分布。
通过直方图可以判断数据是否符合正态分布。
正态概率图则可以用来判断数据是否符合正态分布。
正态概率图展示了数据的累积分布情况,如果数据点大致沿着一条直线分布,那么可以认为数据符合正态分布。
盒须图可以展示数据的五个关键统计量:最小值、第一四分位数、中位数、第三四分位数和最大值。
通过盒须图可以判断数据的分布情况和离群值的存在情况。
除了这些统计工具之外,还可以计算数据的均值、标准差和过程能力指数等。
均值反映了数据的中心趋势,标准差反映了数据的分布范围。
CPK分析的结果可以帮助我们评估产品质量的合格程度,优化生产过程,并进行过程改进。
质量控制的过程能力分析

质量控制的过程能力分析质量控制是企业在生产过程中确保产品或服务符合既定标准和客户需求的一系列活动。
为了提高产品质量和生产效率,企业需要进行过程能力分析,以评估生产过程中的稳定性和一致性,并及时采取控制措施。
一、什么是过程能力分析过程能力分析是通过统计方法对生产过程进行全面评估,以量化生产过程的能力和稳定性。
它可以帮助企业确定生产过程是否稳定、一致,并且是否满足产品质量要求。
通过过程能力分析,企业可以发现潜在的问题,以及改进和控制的机会。
过程能力分析的关键指标包括过程能力指数(CP)和过程能力指数的指定(CPK)。
过程能力指数表示生产过程的能力和稳定性,一般要求大于1.33才能被认为是合格的。
而过程能力指数的指定则进一步考虑了过程的中心位置和离散程度,综合评估了生产过程的能力。
二、过程能力分析的步骤过程能力分析通常包括以下步骤:1. 确定关键过程特性:首先,企业需要确定需要进行能力分析的关键过程特性。
这些特性可以是产品的物理特性、技术指标或者其他重要的质量要求。
2. 收集数据:接下来,企业需要收集与关键过程特性相关的数据。
这些数据应该来自真实的生产环境,并且应该具有一定的代表性。
3. 统计分析:企业可以使用统计方法对收集到的数据进行分析。
常用的方法包括计算均值、标准差、离散程度等。
4. 计算过程能力指数:根据分析得到的数据,企业可以计算过程能力指数(CP)和过程能力指数的指定(CPK)。
5. 结果判断:最后,根据过程能力指数的计算结果,判断生产过程的能力和稳定性。
如果CP和CPK值都大于1.33,说明生产过程具有足够的能力满足产品质量要求。
否则,企业需要进一步分析原因,并采取相应的控制措施。
三、过程能力分析的应用过程能力分析可以帮助企业实现持续改进和质量控制。
通过分析过程能力,企业可以找到生产过程中的问题和瓶颈,并采取相应的控制和改进措施。
1. 提高生产效率:通过过程能力分析,企业可以确定生产过程是否稳定和一致。
CPK过程能力分析
- 名称不同:Cpk是过程能力指数,Ppk是过程性能指数.
- 实施时机不同:Cpk一般是量产时实施,Ppk一般试生产时实施. 我们默认为稳定状态下连续抽样表征了量产的状况,所以新飞通目前 采取了在试产阶段控制Cpk的方式
12
600.4 599.6 600.0 600.8 600.4
13
599.4 599.0 598.4 599.0 599.6
14
598.8 599.2 599.6 598.6 599.8
5
6
598.8 598.8 599.8 599.2 599.4
600.0 600.2 600.2 599.6 599.0
案例-步骤4
用 ppm表示实际DATA脱离规格的程度。
案例-步骤4
只考虑工程的群内变动显示正态分布时,数据表现为 脱离规格的预想 ppm
案例-步骤4
对所有DATA的变动值来显示正态分布时, DATA表现脱离规格的预测 ppm
提高过程能力的思路
常犯的错误或常见问题
✓ 工艺过程不处于稳定状态,有异常发生时进行过程 性能分析
✓ 样本数量太少 ,不具备代表意义
✓ 有明显因为各种特殊原因导致的明显有问题的数 据,没做剔除而保留下来,影响了整体分析的结果
✓ 对计算结果的意义不了解,没有制定很好的改善 措施
回顾与讨论
过程能力分析的前提条件是什么? CP与CPK,PP与PPK之间的区别是什么? CPK与PPK之间的区别是什么? CP>1.67而 CPK<1.0的时候,应该如何处理? CP<1.0的时候,又该如何处理
PCA-过程能力(CPK)分析
过程能力的应用
▪ 过程能力指数代表了过程能力的高低,过程能力指数越大表明 对应的过程能力越高。一般说来对过程能力的评价标准为:
Cpk的取值范围
级别
过程能力的评价
Cpk≥1.67 1.67> Cpk≥1.33 1.33> Cpk≥1.0 1.0>Cpk≥0.67 0.67>Cpk
Ⅰ
过程能力较高
Ⅱ
过程能力充分
•影响过程质量的6个因素(6M)
—人员 —设备 —材料 —方法 —测量 —环境
• 6M导致的变异有两种
—随机性变异 —系统性变异
• 如果过程仅受随机性因素的影响,那么一般情况 下,过程质量特征值服从正态分布
PCA-过程能力(CPK)分析
过程能力分析的基本概念
99.73%
±3 过程能力=B= ±3= ±3S
PCA-过程能力(CPK)分析
过程能力分析的基本概念
▪ 过程能力是指过程的一致性,显然,过程的变 异是衡量过程质量特征值的一致性的指标
▪ 过程能力指数(CPK):指过程的加工质量满 足技术标准的程度。
▪ 两种变异: • 特定时点的本质或内在变异 • 一段时间内的变异
PCA-过程能力(CPK)分析
过程能力分析的基本概念
PCA-过程能力(CPK)分析
目录
▪ 过程能力分析的目的和步骤 ▪ 如何进行合理抽样 ▪ 过程稳定性分析 ▪ 过程数据正态性分析 ▪ CP/CPK的计算方法和应用方法 ▪ 属性型数据质量统计指标
PCA-过程能力(CPK)分析
过程稳定性分析
过程稳定的意义
一个稳定的过程仅存在随机性变异 通过稳定性可以检验是否存在系统性变异,如果存在 系统性变异,在进行PCA之前应剔除
过程能力研究报告
过程能力研究报告过程能力研究报告引言过程能力是指一个系统或组织在特定过程中实现目标的能力。
在现代企业管理中,过程能力研究成为重要的课题,因为提高过程能力可以帮助企业提升效率、降低成本、改进质量,进而增强竞争力。
本报告旨在通过对过程能力的研究,从理论和实践两个方面,探究过程能力的重要性以及提高过程能力的方法。
理论研究过程能力的定义过程能力是指一个系统或组织在特定过程中实现目标的能力。
它包括两个方面的要素:过程的可控性和过程的稳定性。
过程的可控性意味着能够对过程进行控制,使其达到预期的结果;过程的稳定性意味着过程能够持续稳定地运行,不受随机因素的干扰。
过程能力的评估可以通过CPK指数来衡量,CPK指数代表了过程性能与规格界限之间的差值。
CPK值越高,说明过程能力越好。
过程能力的重要性过程能力的提高对企业来说非常重要。
首先,过程能力的提升可以帮助企业提高效率。
通过分析和改进各个环节的过程,可以消除浪费,减少资源的浪费,从而使企业更加高效地运营。
其次,过程能力的提高可以降低成本。
通过提高过程的稳定性和可控性,能够减少不良事件的发生,降低质量问题的成本和损失。
最后,过程能力的提高可以改进质量。
通过对过程进行分析和改进,可以减少变异性,提高产品或服务的一致性,从而提高客户满意度。
实践研究过程能力改进的方法1.流程分析与优化:通过对流程进行分析,找出流程中的瓶颈和问题,并进行优化,以提高过程的效率和稳定性。
2.数据收集与分析:对关键指标进行数据收集和分析,通过数据的监控和分析,可以追踪过程的变化和趋势,及时发现问题并采取措施进行改进。
3.培训与技能提升:提供员工培训,提高员工对过程的理解和掌握,增强员工的能力和素质,从而推动过程能力的提升。
4.技术支持与工具应用:通过应用先进的技术和工具,可以提高过程的自动化程度、减少人为干预,从而提高过程的稳定性和可控性。
实践案例分析案例一:制造业流程改进某制造企业的生产流程中存在着很多问题,如物料供应不及时、生产线停机等。
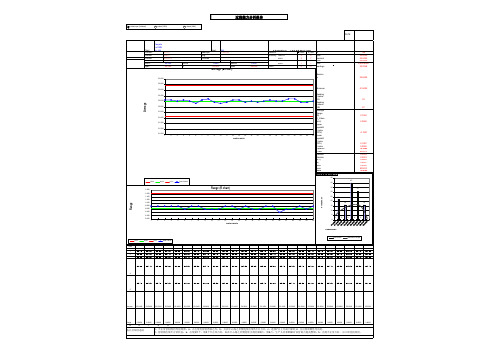
关键过程能力调查(CPK)报告
关键过程能力调查(CPK )报告QR/QSP-07-3工厂车间车间工序名称产品成型质量特性重量公差上限8.62 组容/频率125生产形态 试样生产产品名称左右行李架总成产品型号A5700470/A5700480规格值8.12±0.5公差下限7.62 图 号日 期2017.9.10●X=AVE (X )=8.13UCL X =X+A 2R=8.30LCL X =X-A 2R=7.96说 明 栏AVERAGES (X BAR CHART )●对特殊原因采取措施说明*任何超出控制限的点*连续7点在中心线之上或之下*连续7点上升/下降*任何其它明显非随机的图形●采取措施的说明①不要对过程做不必要改变②注明对过程因素(人机料法环或MS)所做的调整③组容A 2D 3D 4d 22 1.88*3.271.13 ●R=AVE (R )=0.233UCL R =D 4R=0.531LCL R =D 3R=0.0003 1.02 * 2.57 1.69 RANGES (R CHART )40.73 * 2.28 2.06 50.58 * 2.11 2.33 60.48 * 2.00 2.53 70.42 0.08 1.92 2.70 80.37 0.14 1.86 2.85 90.34 0.18 1.82 2.97 100.31 0.22 1.783.081.在确定Cpk 前过程必须受控2.组容<7时没有极差下控制限●Cpk = Min (USL-X X-LSL)≥1.333R/d 23R/d 2=Min(1.448 1.500 ) = 1.448 样本序列12345678910111213141516171819202122232425检查记录18.06 8.07 8.25 8.13 8.29 7.95 8.17 8.08 8.26 7.97 8.02 8.24 8.04 8.26 8.16 8.28 8.14 8.17 8.30 8.15 8.03 8.08 8.02 8.25 8.20 28.03 8.12 8.21 8.24 8.30 8.25 8.09 8.11 8.06 8.10 8.07 8.11 7.99 8.05 8.17 8.08 8.01 8.02 8.11 8.01 8.13 7.99 8.04 8.21 7.98 38.00 8.07 8.24 8.12 8.19 8.26 8.28 8.24 8.06 8.27 7.97 8.21 8.15 8.27 8.00 8.07 8.05 8.08 7.96 8.09 8.08 8.11 8.26 8.11 8.20 48.17 8.19 7.99 8.30 8.12 8.25 8.27 8.05 8.23 8.12 8.02 8.18 7.99 8.24 7.95 8.09 8.29 8.04 8.17 8.28 8.25 8.08 7.98 8.04 8.10 58.30 8.28 8.24 8.01 8.25 8.01 8.11 8.18 8.13 8.27 8.18 8.23 7.97 8.28 8.14 8.26 8.29 7.97 8.00 8.04 8.19 7.98 7.98 8.02 8.03 TOTAL 40.56 40.73 40.92 40.80 41.16 40.72 40.91 40.65 40.75 40.73 40.25 40.98 40.14 41.10 40.42 40.79 40.76 40.29 40.53 40.58 40.68 40.24 40.27 40.63 40.51 AVERAGE(X)8.11 8.15 8.18 8.16 8.23 8.14 8.18 8.13 8.15 8.15 8.05 8.20 8.03 8.22 8.08 8.16 8.15 8.06 8.11 8.12 8.14 8.05 8.05 8.13 8.10 CL X 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 8.13 UCL X 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 8.30 LCL X7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 7.96 MAX-MIN(R)0.30 0.21 0.27 0.29 0.18 0.31 0.20 0.20 0.21 0.30 0.21 0.13 0.18 0.24 0.22 0.21 0.28 0.20 0.33 0.27 0.22 0.13 0.28 0.23 0.22 CL R 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 0.23 UCL R 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 0.53 LCL R0.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.00制表/日期:CLLCLUCLUCLUCLCL。
