数字信号处理作业+答案讲解
数字信号处理(第三版)_课后习题答案全_(原题+答案+图)
第 1 章
时域离散信号和时域离散系统
6. 给定下述系统的差分方程, 试判定系统是否是因果稳定系统, 并说明
理由。
1 N 1 N k 0 (2) y(n)=x(n)+x(n+1)
第 1 章
(2) 令输入为
x(n-n0) 输出为
Байду номын сангаас
时域离散信号和时域离散系统
y′(n)=2x(n-n0)+3
y(n-n0)=2x(n-n0)+3=y′(n)
故该系统是非时变的。 由于 T[ax1(n)+bx2(n)]=2ax1(n)+2bx2(n)+3 T[ax1(n)]=2ax1(n)+3 T[bx2(n)]=2bx2(n)+3 T[ax1(n)+bx2(n)]≠aT[x1(n)]+bT[x2(n)] 故该系统是非线性系统。
m
第 1 章
时域离散信号和时域离散系统
题7图
第 1 章
时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章
解法(二)
时域离散信号和时域离散系统
采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
n n0 k n n0
|x(k)|≤|2n0+1|M, 因
此系统是稳定的; 假设n0>0, 系统是非因果的, 因为输出
数字信号处理课后答案

k = n0
∑
n
x[ k ]
(B) T {x[n]} =
∑
x[k ]
(C) T {x[ n]} = 0.5
x[ n ]
(D) T {x[n]} = x[− n]
1-5 有一系统输入为 x[n] ,输出为 y[n] ,满足关系 y[n] = ( x[n] ∗ u[n + 2])u[n] ,则系统是(A) (A)线性的 (B)时不变的 (C)因果的 (D)稳定的 解:
(a) T { x[ n ]} = h[ n] + x[ n ], (c) T {x[ n]} = ∑ x[ n − k ]
δ [n] + aδ [n − n0 ] ,单位阶跃响应 s[n] = u[n] + au[n − n0 ] 。
1-15 线性常系数差分方程为 y[n] − y[n − 1] +
y[n] = 0 , n < 0 , 则 y[3] = 0.5 。 解: y[0] = y[ −1] − 0.25 y[ −2] + x[0] = 1 y[1] = y[0] − 0.25 y[ −1] + x[1] = 1 y[2] = y[1] − 0.25 y[0] + x[2] = 0.75 y[3] = y[2] − 0.25 y[1] + x[3] = 0.5
∞ ∞ k =−∞ n '=−∞
解: (a)
n =−∞
∑ y[n] = ∑ ∑ x[k ]h[n − k ] = ∑ x[k ] ∑ h[n − k ] = ∑ x[k ] ∑ h[n ']
n =−∞ k =−∞ k =−∞ n =−∞
∞
∞
∞
《数字信号处理》第三版课后习题答案

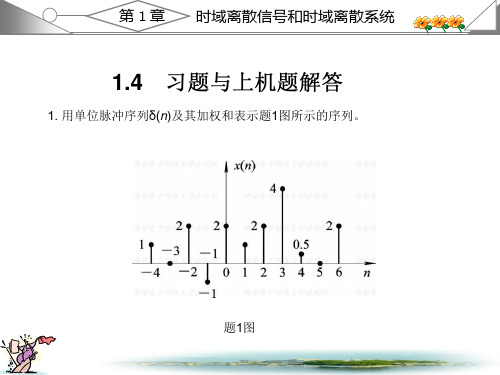
《数字信号处理》第三版课后习题答案数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-??=≤≤其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列;(3)令1()2(2)x n x n =-,试画出1()x n 波形;(4)令2()2(2)x n x n =+,试画出2()x n 波形;(5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理习题答案及matlab实验详解.pdf

阶跃响应为: y[n] x[n] h[n] x[m]h[n m] h(n m), n m, m 0
m
m0
即 y(0) 0, y(1) 0.25, y(2) 0.5, y(3) 0.75,其余y(n) 1, (n 3)
利用函数 h=impz(b,a,N)和 y=filter(b,a,x)分别绘出冲激和阶跃响应 b=[0,0.25,0.25,0.25,0.25]; a=1; x=ones(1,100); h=impz(b,a,100);y=filter(b,a,x) figure(1) subplot(2,1,1); stem(h,’.’); subplot(2,1,2); plot(y,’.’);
4
解:(1)系统的转移函数是是其单位抽样响应的 Z 变换,因此
H (z)
1 1 z1
1 1 0.3z1
1 1 0.6z1
(1
3 3.8z1 1.08z2 z1)(1 0.3z1)(1 0.6z1)
1
3 1.9
3.8z1 1.08z2 z1 1.08z2 0.18z
3
Z 1
系统的零极点图如下图所示: B=[3,-3.8,1.08]; A=[1,-1.9,1.08,-0.18]; [Z,P,K]=tf2zp(B,A); Zplane(B,A)
5
单位抽样响应:
h(n)
1 2
n1
u
(n
1)
(n)
1
y(n) x(n) * h(n)
2 m1
1 2
m1
e
j (n m)
e
jn
e
jn
e j
1 2 1
2
n
u(n1)
数字信号处理习题及答案解析

==============================绪论==============================1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章 时域离散时间信号与系统==================1.①写出图示序列的表达式答:3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的, 确定其周期。
(1)A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= (2))81(j e )(π-=n n x 解: (1) 因为ω=73π, 所以314π2=ω, 这是有理数, 因此是周期序列, 周期T =14。
(2) 因为ω=81, 所以ωπ2=16π, 这是无理数, 因此是非周期序列。
③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。
3.加法乘法序列{2,3,2,1}与序列{2,3,5,2,1}相加为__{4,6,7,3,1}__,相乘为___{4,9,10,2} 。
移位翻转:①已知x(n)波形,画出x(-n)的波形图。
②尺度变换:已知x(n)波形,画出x(2n)及x(n/2)波形图。
卷积和:①h(n)*求x(n),其他02n 0n 3,h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤= }23,4,7,4,23{0,h(n)*答案:x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5},则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3),求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案:x(n)=4.如果输入信号为,求下述系统的输出信号。
数字信号处理习题解答

y(5)=2*1+1*2=4;y(6)=2*3+1*1+3*2=13 y(7)=1*3+3*1=6;y(8)=3*3=9
y(9)=0;
• N=10圆卷积的结果
10 13 9
6
4
4
1
2
n
0
补充作业
x(n)
22
1
1
n
0
求: (1)x(n)*x(n)的线卷积。
,N=4(不加长)
,N=6(补零加长)
,N=7(补零加长)
作业解答
lfhuang
第一次作业: P104页,3题
...
...
0
n
0
n
第一次作业: P104页,3题
第一次作业: P104页,3题
4
...
1
.k .
0
第二次作业: P104页,4题
第二次作业: P104页,4题
... ... ...
... 图a
n
...
图b n
...
图c n
第二次作业: P104页,4题
3
2
1
1
n
0
周期化
3
2
1
1
n
0
3
3
3
1
2 1
12 1
1
2 1
0
0
n
反折、取主值区间。
3 2
11
0
右平移、相乘、相加 y(0)=1*1+2*1+1*2=5 y(1)=2*3+1*1+3*2=13 y(2)=1*2+2*1+1*3+3*3=16
数字信号处理》课后作业参考答案
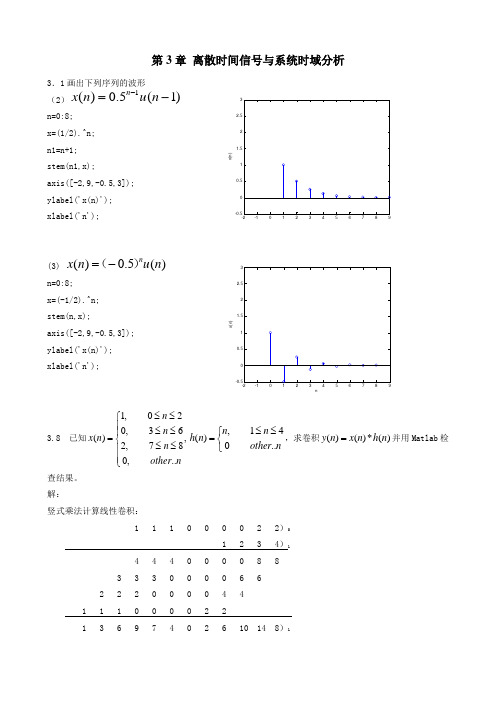
第3章 离散时间信号与系统时域分析3.1画出下列序列的波形(2)1()0.5(1)n x n u n -=- n=0:8; x=(1/2).^n;n1=n+1; stem(n1,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');(3) ()0.5()nx n u n =-()n=0:8; x=(-1/2).^n;stem(n,x);axis([-2,9,-0.5,3]); ylabel('x(n)'); xlabel('n');3.8 已知1,020,36(),2,780,..n n x n n other n≤≤⎧⎪≤≤⎪=⎨≤≤⎪⎪⎩,14()0..n n h n other n≤≤⎧=⎨⎩,求卷积()()*()y n x n h n =并用Matlab 检查结果。
解:竖式乘法计算线性卷积: 1 1 1 0 0 0 0 2 2)01 2 3 4)14 4 4 0 0 0 0 8 83 3 3 0 0 0 0 6 62 2 2 0 0 0 0 4 41 1 1 0 0 0 02 21 3 6 9 7 4 02 6 10 14 8)1x (n )nx (n )nMatlab 程序:x1=[1 1 1 0 0 0 0 2 2]; n1=0:8; x2=[1 2 3 4]; n2=1:4; n0=n1(1)+n2(1);N=length(n1)+length(n2)-1; n=n0:n0+N-1; x=conv(x1,x2); stem(n,x);ylabel('x(n)=x1(n)*x2(n)');xlabel('n'); 结果:x = 1 3 6 9 7 4 0 2 6 10 14 83.12 (1) 37πx (n )=5sin(n) 解:2214337w πππ==,所以N=14 (2) 326n ππ-x (n )=sin()-sin(n)解:22211213322212,2122612T N w T N w N ππππππ=========,所以(6) 3228n π-x (n )=5sin()-cos(n) 解:22161116313822222()T N w T w x n ππππππ=======,为无理数,所以不是周期序列所以不是周期序列3.20 已知差分方程2()3(1)(2)2()y n y n y n x n --+-=,()4()nx n u n -=,(1)4y -=,(2)10,y -=用Mtalab 编程求系统的完全响应和零状态响应,并画出图形。
数字信号处理第三章习题作业答案

1 e 当 k 2, 4, 6,... 时,X 1 (k ) 0
序列3:
x3 (n) x1 (n) x1 (n 4)
根据序列移位性质可知
X 3 (k ) X1 ( k ) e j k X1 ( k ) (1 e j k )
即 x(n) 是以 n 0 对称轴的奇对称
故这三个序列都不满足这个条件
(3)由于是8点周期序列,其DFS:
nk X (k ) x(n )WN x (n )e n 0 n 0 N 1 7 j 2 nk 8
序列1:
X 1 (k ) e
n 0
3
y 解: 序列 x(n) 的点数为 N1 6 , (n) 的点数为 N 2 15, 故 x(n) y (n) 的点数应为
N N1 N 2 1 20
是线性卷积以15为周期周期延拓后取主值序列 19( N 1) 0
15 ( L)
又 f (n) 为 x(n) 与 y (n) 的15点的圆周卷积,即L=15。
第三章习题讲解
n 1, 0 n 4 h(n) R4 (n 2) 3.设 x(n) 其他n 0, h 令 x(n) x((n))6 , ( n) h((n)) 6 ,
试求 x(n) 与 h (n) 的周期卷积并作图。
解:
y ( n ) x ( m )h ( n m )
4 ( L N 1)
15 ( L)
34 ( L N 1)
混叠点数为N-L=20-15=5 n 0 ~ n 4( N L 1) 故 f (n)中只有 n 5到 n 14的点对应于 x(n) y (n)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理作业哈尔滨工业大学2006.10DFT 习题1. 如果)(~n x 是一个周期为N 的周期序列,那么它也是周期为N 2的周期序列。
把)(~n x 看作周期为N 的周期序列,令)(~1k X 表示)(~n x 的离散傅里叶级数之系数,再把)(~n x 看作周期为N 2的周期序列,再令)(~2k X 表示)(~n x 的离散傅里叶级数之系数。
当然,)(~1k X 是周期性的,周期为N ,而)(~2k X 也是周期性的,周期为N 2。
试利用)(~1k X 确定)(~2k X 。
(76-4)2. 研究两个周期序列)(~n x 和)(~n y 。
)(~n x 具有周期N ,而)(~n y 具有周期M 。
序列)(~n w 定义为)()()(~~~n y n x n w +=。
a. 证明)(~n w 是周期性的,周期为MN 。
b. 由于)(~n x 的周期为N ,其离散傅里叶级数之系数)(~k X 的周期也是N 。
类似地,由于)(~n y 的周期为M ,其离散傅里叶级数之系数)(~k Y 的周期也是M 。
)(~n w 的离散傅里叶级数之系数)(~k W 的周期为MN 。
试利用)(~k X 和)(~k Y 求)(~k W 。
(76-5)3. 计算下列各有限长度序列DFT (假设长度为N ):a. )()(n n x δ= b .N n n n n x <<-=000)()(δc .10)(-≤≤=N n an x n(78-7)4. 欲作频谱分析的模拟数据以10千赫速率被取样,且计算了1024个取样的离散傅里叶变换。
试求频谱取样之间的频率间隔,并证明你的回答。
(79 -10)5. 令)(k X 表示N 点序列)(n x 的N 点离散傅里叶变换(a ) 证明如果)(n x 满足关系式:)1()(n N x n x ---=,则0)0(=X 。
(b ) 证明当N 为偶数时,如果)1()(n N x n x --=,则0)2/(=N X 。
(80-14)6. 令)(k X 表示N 点序列)(n x 的N 点离散傅里叶变换,)(k X 本身也是一个N 点序列。
如果计算)(k X 的离散傅里叶变换得到一序列)(1n x ,试用)(n x 求)(1n x 。
(82-15)7. 若)(n x 为一个N 点序列,而)(k X 为其N 点离散傅里叶变换,证明:∑∑-=-==10k 212)k (X N 1)(N N n n x ,这是离散傅里叶变换的帕斯维尔关系式。
(82-16)8. 长度为8的一个有限时宽序列具有8点离散傅里叶变换)(k X ,如图所示。
长度为16的一个新的序列)(n y 定义为:⎪⎩⎪⎨⎧=为奇数为偶数n n nx n y 0)2()(,试画出相当于)(n y 的16点离散傅里叶变换的略图。
(86页-18)k0 1 2 3 4 5 679. 令()x n 表示z 变换为()X z 的无限时宽序列,而1()x n 表示长度为N 的有限时宽序列,其N 点离散傅立叶变换用1()X k 表示。
如果()X z 和1()X k 有如下关系:1()()|, 0,1,2,,1k Nz W X k X z k N -===-式中2jNN W eπ-=。
试求()x n 和1()x n 之间的关系。
(93-22)10. 令)(ωj eX 表示序列)()2/1()(n u n x n =的傅里叶变换,并令)(n y 表示长度为10的一个有限时宽序列,即0<n 时,0)(=n y ,10>n 时,0)(=n y ,)(n y 的10点离散傅里叶变换用)(k Y 表示,它相当于)(ωj e X 的10个等间隔取样,即)()(10/2k j e X k Y π=,试求)(n y (94-23)11. 讨论一个长度为N 的有限时宽序列)(n x ,0<n 和1->N n 时,0)(=n x ,我们要求计算其z 变换)(z X 在单位圆的M 个等间隔点上的取样。
取样数M 小于序列的时宽N ;即N M ≤,试求一种得到)(z X 的M 个取样的方法,它只要计算一次M 点序列(这个序列是由)(n x 得来的)的M 点离散傅里叶变换。
(96-25)12. 研究两个0<n 时等于零的有限时宽序列)(n x 和)(n y ,且时当时当20n 0)(8n 0)(≥=≥=n y n x ,将每一个序列的20点离散傅里叶变换,然后计算离散傅里叶反变换,令)(n r 表示它的离散傅里叶反变换,指出)(n r 的哪些点相当于)(n x 与)(n y 线性卷积中的点。
(96-26)FFT 习题1. 假设有一计算如下离散傅里叶变换的程序:1,...,1,0)()(1)/2(-==∑-=-N k e n x k X N n knN j π,试指出如何用此程序来计算如下反变换:1,...,1,0)(1)(1)/2(-==∑-=-N n ek X Nn x N k knN j π(193-8)2. 在计算实序列的离散傅里叶变换时,利用序列是实序列这一特点有可能减少计算量,本题中讨论了两种减少计算量的途径:a. 研究两个分别具有离散傅里叶变换1()X k 和2()X k 的实序列1()x n 和2()x n ,令()g n 为一个复序列,12()()()g n x n jx n =+,()G k 为其离散傅里叶变换。
令()OR G k 、()ER G k 、()OI G k 、()EI G k 分别表示()G k 的实部的奇数部分、实部的偶数部分、虚部的奇数部分和虚部的偶数部分,试利用()OR G k 、()ER G k 、()OI G k 和()EI G k 表示1()X k 和2()X k 。
b. 假设()x n 是一个N 点的实序列,且N 可以被2整除,令1()x n 和2()x n 为两个/2N 点序列,其定义为:1()(2),0,1,2,...,/21x n x n n N ==-, 2()(21),0,1,2,...,/21x n x n n N =+=-试利用1()X k 和2()X k 求()X k 。
(198-10)3. 研究一个有限长度序列)(n x ,并且0n n <和01n N n +->时,0)(=n x 。
假设我们想要计算在z 平面内下列各点上)(n x 的z 变换之取样:))/2((k M j k re z πθ+=,1,...,2,1,0-=M k ,式中N M <。
试详细说出一种计算这些点上的)(z X 的有效方法。
(199页-11)4. 研究一个长度为M 的有限时宽序列)(n x ,并且0<n 和M n >时,0)(=n x 。
我们希望计算z 变换∑-=-=1)()(N n nzn x z X 在单位圆上N 个等间隔点上的取样,即在k N j e z )/2(π=,1,...,2,1,0-=N k 上的取样,试找出对下列情况只用一个N 点离散傅里叶变换就能计算)(z X 的N 个取样的方法,并证明之。
(a ) M N ≤(b ) M N >(200-12)5.)(ωj e X 表示长度为10的有限时宽序列)(n x 的傅里叶变换,我们希望计算)(ωj e X 在频率)9,...1,0)(100/2(2==k k k πω时的10个取样。
计算时不能采取先算出比要求多的取样,然后再丢掉一些的办法。
讨论采用下列各方法的可行性: (a) 直接利用10点快速傅里叶变换算法。
(b) 利用线性调频z 变换算法。
(201-13)6. 在下列说法中选择正确的结论并加以证明。
线性调频z 变换可以用来计算一个有限时宽序列()h n 在z 平面实z 轴上诸点{}k z 的z 变换()H z ,使a) ,0,1,...,1,kk z a k N a ==-≠±为实数,a 1; b) ,0,1,...,1,0kk z a k N a ==-≠为实数,ac) a)和b)两者都行;d) a)和b)都不行,即线性调频z 变换不能计算()H z 在z 为实数时的取样。
(203-15)Hilbert 变换习题1. 令()x n 为()x n <∞的一个实因果序列,已知()x n 的z 变换为 0()()nn X z x n z∞-==∑上式为变量1z -的泰勒级数,所以它在以z=0为中心的某一圆外部处处收敛于一个解析函数。
[收敛区域包括点z=∞,事实上,()(0)X x ∞=]。
我们说()X z 是解析(在其收敛区域内)的,表示对X 加了苛刻的约束条件,即它的实部和虚部各都满足拉普拉斯方程,且实部和虚部之间满足柯西-黎曼方程。
现在我们利用这些性质,根据()X z 的实部确定()X z ,条件是()x n 为有限值的实因果序列。
令()x n 为实(有限值的)因果序列,其z 变换为:()()()R I X z X z jX z =+式中:R X 和I X 是z 的实函数。
假设j ze ωρ=时,R X 给定为cos ()j R X e ωραωρρ+=(α为实数)假设除了z=0外,()X z 处处解析,试求()X z 并表示成z 的显函数。
(建议用时域法解此题)(214-4)2. 序列()x n 的偶部定义为:()()()2e x n x n x n +-=,假设()x n 是一个有限时宽实序列,定义为0n <和n N ≥时,()0x n =。
令()X k 表示为()x n 的N 点的离散傅立叶变换。
(a )()e x n 的离散傅立叶变换是否等于Re[()X k ]?(b )试求出以()x n 表示的Re[()X k ]的离散傅立叶反变换。
(228-15)3. 研究一个长度N 的有限时宽实序列(即n<0,n ≥N 时,()x n =0),此处N 为奇数。
用()X k 表示()x n 的M 点的离散傅立叶变换,因此令()R X k 表示()X k 的实部。
(a ) 试利用N 来求能使()R X k 唯一确定()X k 的最小M 值(M=1,2除外)。
(b ) 如果M 满足(a )中所确定的条件,则()X k 可以表示为()R X k 和序列()U k 的循环卷积。
请确定()U k 。
(228-16)1(2/)0()()N j M nkn X k x n e π--==∑4.研究一个复序列x(n),x(n)=xr(n)+xi(n),其中xr(n)和xi(n)是实序列,序列x(n)的z变换X(z)在单位圆的下半部分为零。
即,π≤ω≤2π时,X(ejω)=0. x(n)的实部为x r(n)=1/2,01/4,2 0,nn=⎧⎫⎪⎪-=±⎨⎬⎪⎪⎩⎭其他试求X(e jω)的实部和虚部。
