光栅效率曲线图(典型值)及倒线色散和光谱带宽对照表
合集下载
高二物理竞赛光栅光谱仪PPT(课件)
第四章 衍射光栅
§1、 光栅光谱仪
光栅的 1）电矢量的 p 反射分量在入射角等于布儒斯特角时发生突变：
缝间干涉极大的光程差条件
能量几乎全部集中到一个
色分辨本领 选用闪耀角为 的光栅，问当平行光以垂
与 成正比，与 无关。
垂直光栅平面方式入射。
1）瑞利判据： （2）自由光谱范围值：
分析红外波段
附近的一级光谱，决定
Nd cos 垂直光栅平面方式入射。
直槽面方向入射时光栅的刻槽密度应为多少？
选用闪耀角为 的光栅，问当平行光以垂
得： （2）自由光谱范围值：
R kN 此时单元衍射零级极大方向
分析红外波段
附近的一级光谱，决定
求在
的一级光谱附近刚能分辨的最小
k d cos
R kN 3）讨论： 与 垂直光栅平面方式入射。
分析红外波段
附近的一级光谱，决定
垂直光栅平面方式入射。
0
b
的反射方向 色分辨本领
1）电矢量的 p 反射分量在入射角等于布儒斯特角时发生突变：
不能说明两条谱线重叠得是否可以分辨，
垂直光栅平面方式入射。
相邻槽面间的入反射光线 两选，条用谱 闪线耀的角最为小波的长光间栅隔，问之当比平行光以垂
色分辨本领
沿此方向的光程差为： 能量几乎全部集中到一个
（2）除与单元零级衍射极强重叠的干涉主极强 外，其余缝间干涉主极强均缺级。
因为：d a
缺级公式变成：
k m d m m 0
a
能量几乎全部集中到一个 非零级彩色干涉主极强上
形成了强烈的 彩色闪耀光谱
4）平行光垂直槽面入射时
在单元衍射零级极强方向上满足 缝间干涉极大的光程差条件
§1、 光栅光谱仪
光栅的 1）电矢量的 p 反射分量在入射角等于布儒斯特角时发生突变：
缝间干涉极大的光程差条件
能量几乎全部集中到一个
色分辨本领 选用闪耀角为 的光栅，问当平行光以垂
与 成正比，与 无关。
垂直光栅平面方式入射。
1）瑞利判据： （2）自由光谱范围值：
分析红外波段
附近的一级光谱，决定
Nd cos 垂直光栅平面方式入射。
直槽面方向入射时光栅的刻槽密度应为多少？
选用闪耀角为 的光栅，问当平行光以垂
得： （2）自由光谱范围值：
R kN 此时单元衍射零级极大方向
分析红外波段
附近的一级光谱，决定
求在
的一级光谱附近刚能分辨的最小
k d cos
R kN 3）讨论： 与 垂直光栅平面方式入射。
分析红外波段
附近的一级光谱，决定
垂直光栅平面方式入射。
0
b
的反射方向 色分辨本领
1）电矢量的 p 反射分量在入射角等于布儒斯特角时发生突变：
不能说明两条谱线重叠得是否可以分辨，
垂直光栅平面方式入射。
相邻槽面间的入反射光线 两选，条用谱 闪线耀的角最为小波的长光间栅隔，问之当比平行光以垂
色分辨本领
沿此方向的光程差为： 能量几乎全部集中到一个
（2）除与单元零级衍射极强重叠的干涉主极强 外，其余缝间干涉主极强均缺级。
因为：d a
缺级公式变成：
k m d m m 0
a
能量几乎全部集中到一个 非零级彩色干涉主极强上
形成了强烈的 彩色闪耀光谱
4）平行光垂直槽面入射时
在单元衍射零级极强方向上满足 缝间干涉极大的光程差条件
光栅常数
d sin
EP E0
sin
1 ei ei2 eiN 1
EP E0
sin
1 ei ei2 eiN 1
N N N i i i 2 e 2 e 2 e
其中 e
d sin k
( k 0,1,2,)
入射光为白光时， 不同， k 不同，按波长分开形成光谱.
I
sin
ab
0
一级光谱 二级光谱
三级光谱
I
sin
ab
0
一级光谱 二级光谱
三级光谱
例如 二级光谱重叠部分光谱范围
d sin 3紫
d sin 2
2-8 衍射光栅(Diffracting Grating) 1 光栅的结构和衍射 大量相同的狭缝等间隔平行地排列就构成一个光栅。
衍射光栅
光栅的衍射：
多缝夫琅和费衍射 的实验装置
光栅的衍射花样： 用柱面透镜时
用圆透镜时
2 正入射照明时光栅的衍射强度
P点的光场时为所有狭缝 的贡献之和
第m个单缝在观察屏上P点
0,
2
,
,,
N 1
, ,
N 1
,,
2N 1
, 2 ,
N N N N N 2 N 1 N 1 2N 1 d sin 0, , ,, , , , , , 2 , N N N N N
N-1个极小 N-1个极小 主极大
sin 0
N-1个极小中还有N-2 个次级大：
N tan tan N
干 涉 因 曲 子 线 的 分 布 光 栅 分 衍 布 射 曲 强 线 度 的
光学：衍射光栅
1、光栅（grating）
任何具有周期性的空间结构或周期性的光学性能 的衍射屏，都可叫作光栅。
2、光栅的种类：
透射光栅
反射光栅
d
d
3、光栅常数 空间周期d
光栅的衍射场鲜明地表现出 “多光束干涉”的基本特征
§1 多缝夫琅和费衍射
1.1 实验装置和衍射图样
缝平面 G L
d
S*
观察屏 p
0
缝平面
d = a+b
闪耀角： b
光栅宏观平面法线方向：
N
单元槽面法线方向：
n
光栅常数，空间周期：d
单元槽面长度： a d
b
n
d
N
闪耀光栅
闪耀光栅照明方式1:
平行于 n 方向。
单元槽面衍射因子的0级角位置： b
d=a
sinb sin ’ -2 -1 0 1 ( /a)
b
n
d
N ’= - b
槽面之间干涉因子，在 b 方向光程差为：2d sinb
sin1
1
M
d
sin2
2
m
d
要求 sin1 sin2 才可分辨
即 M 2m
或
m
1 2
M
2.3、闪耀光栅
反射式光栅： 可以只保留某一级光谱； 能量集中到这一级光谱上。
反射光栅
d
d=2a
sin
-2 -1 0 1 2 3 4
( /d )
透射光栅光谱
d=a
sin
-1 -0
1
2( /d )
闪耀光栅光谱
闪耀光栅各参数：
对于满足 2d sinb 11b
d=a
的 1b ，在 b 有1级主极强。
任何具有周期性的空间结构或周期性的光学性能 的衍射屏，都可叫作光栅。
2、光栅的种类：
透射光栅
反射光栅
d
d
3、光栅常数 空间周期d
光栅的衍射场鲜明地表现出 “多光束干涉”的基本特征
§1 多缝夫琅和费衍射
1.1 实验装置和衍射图样
缝平面 G L
d
S*
观察屏 p
0
缝平面
d = a+b
闪耀角： b
光栅宏观平面法线方向：
N
单元槽面法线方向：
n
光栅常数，空间周期：d
单元槽面长度： a d
b
n
d
N
闪耀光栅
闪耀光栅照明方式1:
平行于 n 方向。
单元槽面衍射因子的0级角位置： b
d=a
sinb sin ’ -2 -1 0 1 ( /a)
b
n
d
N ’= - b
槽面之间干涉因子，在 b 方向光程差为：2d sinb
sin1
1
M
d
sin2
2
m
d
要求 sin1 sin2 才可分辨
即 M 2m
或
m
1 2
M
2.3、闪耀光栅
反射式光栅： 可以只保留某一级光谱； 能量集中到这一级光谱上。
反射光栅
d
d=2a
sin
-2 -1 0 1 2 3 4
( /d )
透射光栅光谱
d=a
sin
-1 -0
1
2( /d )
闪耀光栅光谱
闪耀光栅各参数：
对于满足 2d sinb 11b
d=a
的 1b ，在 b 有1级主极强。
大学物理：衍射光栅 光栅光谱
主要内容：
1. 线偏振光 2. 圆偏振光和椭圆偏振光 3. 自然光
15.11.1 线偏振光
振动面
y
O
z
E
x
y
15.11.2 圆偏振光和椭圆偏振光
1.圆偏振光
O
右旋圆偏振光
理学院 物理系 陈强
线偏振光的表示法
•••••
(光矢量垂直板面)
(光矢量平行板面)
(光矢量与板面斜交)
x
c
z
截面图
叠加图
左旋圆偏振光
理学院 物理系 陈强
§15.9 衍射光栅 光栅光谱
主要内容：
1.衍射光栅 2.光栅光谱
15.9.1 衍射光栅
理学院 物理系 陈强
衍射光栅: 利用多缝衍射原理使光发生色散的元件.
1. 衍射光栅参数
a
光栅常数
d ab
总缝数
b
光栅宽度为 l mm, 每毫米缝
数为 m , 总缝数 N ml
2. 光栅衍射现象 λ
偏振片是一种光学器件. 利用偏振片可以从自然光中获得线偏振光或者改变入射光 的偏振态.
2.起偏和检偏
起起偏偏器器 起偏器 检 检偏 偏器 器 检偏器
自 自••然然光光•• II00自•• •然光• I0•
偏振化方向
线线偏 偏振 振光 光线II 偏振光I α
II
11 22
II
00
I
1 2
I
0
I
I10I 2
主要内容：
1. X射线 2. 布拉格公式
1. X射线
理学院 物理系 陈强
X射线是波长很短的电磁波，波长范围在10-11m~10-8m .
2. 晶体
1. 线偏振光 2. 圆偏振光和椭圆偏振光 3. 自然光
15.11.1 线偏振光
振动面
y
O
z
E
x
y
15.11.2 圆偏振光和椭圆偏振光
1.圆偏振光
O
右旋圆偏振光
理学院 物理系 陈强
线偏振光的表示法
•••••
(光矢量垂直板面)
(光矢量平行板面)
(光矢量与板面斜交)
x
c
z
截面图
叠加图
左旋圆偏振光
理学院 物理系 陈强
§15.9 衍射光栅 光栅光谱
主要内容：
1.衍射光栅 2.光栅光谱
15.9.1 衍射光栅
理学院 物理系 陈强
衍射光栅: 利用多缝衍射原理使光发生色散的元件.
1. 衍射光栅参数
a
光栅常数
d ab
总缝数
b
光栅宽度为 l mm, 每毫米缝
数为 m , 总缝数 N ml
2. 光栅衍射现象 λ
偏振片是一种光学器件. 利用偏振片可以从自然光中获得线偏振光或者改变入射光 的偏振态.
2.起偏和检偏
起起偏偏器器 起偏器 检 检偏 偏器 器 检偏器
自 自••然然光光•• II00自•• •然光• I0•
偏振化方向
线线偏 偏振 振光 光线II 偏振光I α
II
11 22
II
00
I
1 2
I
0
I
I10I 2
主要内容：
1. X射线 2. 布拉格公式
1. X射线
理学院 物理系 陈强
X射线是波长很短的电磁波，波长范围在10-11m~10-8m .
2. 晶体
光栅
单缝衍射因子中央主极大值的角宽度：
(13)
光栅衍射第j个主极大值中心的角位置：
(14)
相邻第一极小值的角位置：
(15)
第j个主极大条纹的半角宽度：
(16)
相邻两个主极大值条纹的角间距：
(17)
结论：
① 光栅衍射主极大值条纹的半角宽度正比于照射光的波长，反比于狭缝数 目及光栅常数，并随着衍射角的增大而增大。当狭缝数目很大时，主极 大值条纹将变为一明细的亮线，即光栅的衍射谱线。
满足这一关系的波长范围，称为光谱仪在该衍射级的自由光谱范围。对于1
级光谱：lm> lM/2。
由于透镜总是存在色差问题，实际光谱仪中都尽量 避免适用透镜进行光谱成像，而是采用凹面反射镜来会聚 衍射光谱。因为反射镜系统是理想的消色差系统。有的光 栅光谱仪直接采用凹面反射式光栅，既作为分光器件，又 作为成像器件，从而大大简化了光路系统。
表面变形
表面等高线
图4.4-19 莫阿条纹的应用
结论：云纹效应反映了相互叠置的两光栅之间的微小差异。这种差异越小，
所引起的莫阿条纹间距Dx越大。前者是微小量，后者则是宏观量。
通过常规方法对莫阿条纹的测量，即可推算出两光栅的微小差异。
利用这一原理，可检测光栅或网格的质量、测量工程材料或结构件
的应力、应变，测量物体的三维面形，以及微小位移和速度等。
② 主极大值位置与狭缝数目无关，但其强度大小正比于狭缝数目的平方及 单缝衍射强度因子。因此，一方面主极大值中心点的光强度随狭缝数目
的增大而增大；另一方面，各级主极大值中心点的相对强度又按sinc2a
形式分布，中央主极大值中心点的光强度最大。
③ 随着狭缝数目的增大，次极大值强度越来越小，并以各主极大值点为中 心向两侧依次减弱。当N很大时，最大的次极大值强度不超过主极大值 的1/23。因此，一般情况下衍射光能量主要集中在各主极大值条纹上。
光栅-PPT精品文档
8
干涉条纹主极大 的位置没有变化， 但主极大的强度 受到衍射的调制 而变化；并且出 现了亮纹缺级现 象。
d 例 . N = 4， a = 4
I单
I0 单 单缝衍射 sin 2 ( /a) 多缝干涉
-2
-1
0
1
I
I 光栅衍射 光强曲线 -8 -4 N2I0单
的情形
sin
0
主极大缺±4,±8级。
N=4 单缝衍射 d = 4a 轮廓线 缺级 sin 4 8 ( /d )
9
1.缺级现象分析： 当某衍射角θ方向既是多光束干涉的某一级主极 大，又是单缝衍射光强为零的方向时，此时在应 该干涉加强的位置没有衍射光到达，从而在光谱 中缺少这一级亮条纹的现象， 称为缺级现象。
即θ同时满足
d sin k a sin k
( 1 )由 d sin k 求出 sin ;
11
3.能观测到的谱线（主极大）
正入射：
max
d sin k
k max
d
应呈现2k +1条，减去缺极即能观测到的谱线
斜入射：
d (sin sin ) k
P
( 1 sin ) d k m ax
k 0 , 1 , 2 k 1 , 2 , 3
d k k k 1 , 2 , 3 a
可见，产生缺级的条件：d/a 为整数比。满足上 述条件时，某些级的条纹消失。 d/a=3,缺3，6，9…级；d/a=5/3,缺5，10，15 …级
10
2.谱线的位置
sin k / d
x ftg
f X
P
一、光栅衍射基本原理分解
N
暗纹间距= 主极大间距 N
相邻主极大间有N－1个暗纹和N－2个次极大。
光栅衍射
例： N = 4,有三个极小：
d sin m
N sin 1 , 2 , 3
4d 4d 4d
k 1 , k 2 , k 3
d sin 2
, , 3
2
4
光栅衍射
d sin 2
做适当的调整，如图所示。在衍射角的方向上，光 程差为
P
A
O
B
斜入射时光栅光程差的计算
A
C
D B
光栅光谱
BD AC （a b）sin (a b) sin (a b)(sin sin )
由此可得斜入射时的光栅方程为
(a b)(sin sin ) k k 0, 1, 2
---光栅方程
6.掠入射x射线谱仪
• 当光谱进入x射线波段时，由于材料对x射 线光的透射率太低，即吸收太大。因此， 透射式光栅已不适用于x射线波段光谱的测 量；
• 而对于反射式光栅，由于材料对x射线光的 吸收较大，即反射率较低。因此，为了适 应x射线波段光谱的测量的要求，采用了能 够提高反射效率的掠入射方式；
光栅光谱
解 （1）根据光栅方程 (a b) si得n k
k
ab
sin
按题意知，光栅常数为
a
b
1 500
mm
2
106
m
可见 k的可能最大值相应于 sin 1
代入数值得
k
2106 589.3109
3.4
k只能取整数 ，故取k=3,即垂直入射时能看到第 三级条纹。
光栅光谱
（2）如平行光以 角入射时，光程差的计算公式应
暗纹间距= 主极大间距 N
相邻主极大间有N－1个暗纹和N－2个次极大。
光栅衍射
例： N = 4,有三个极小：
d sin m
N sin 1 , 2 , 3
4d 4d 4d
k 1 , k 2 , k 3
d sin 2
, , 3
2
4
光栅衍射
d sin 2
做适当的调整，如图所示。在衍射角的方向上，光 程差为
P
A
O
B
斜入射时光栅光程差的计算
A
C
D B
光栅光谱
BD AC （a b）sin (a b) sin (a b)(sin sin )
由此可得斜入射时的光栅方程为
(a b)(sin sin ) k k 0, 1, 2
---光栅方程
6.掠入射x射线谱仪
• 当光谱进入x射线波段时，由于材料对x射 线光的透射率太低，即吸收太大。因此， 透射式光栅已不适用于x射线波段光谱的测 量；
• 而对于反射式光栅，由于材料对x射线光的 吸收较大，即反射率较低。因此，为了适 应x射线波段光谱的测量的要求，采用了能 够提高反射效率的掠入射方式；
光栅光谱
解 （1）根据光栅方程 (a b) si得n k
k
ab
sin
按题意知，光栅常数为
a
b
1 500
mm
2
106
m
可见 k的可能最大值相应于 sin 1
代入数值得
k
2106 589.3109
3.4
k只能取整数 ，故取k=3,即垂直入射时能看到第 三级条纹。
光栅光谱
（2）如平行光以 角入射时，光程差的计算公式应
光栅的色散作用
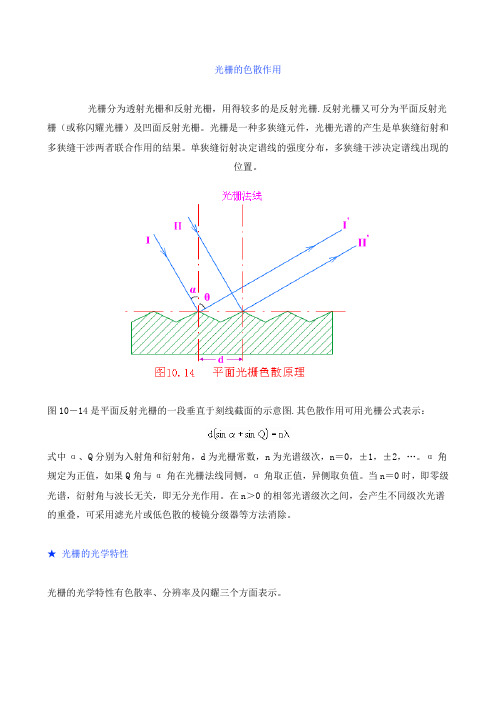
光栅的色散作用光栅分为透射光栅和反射光栅，用得较多的是反射光栅.反射光栅又可分为平面反射光栅（或称闪耀光栅）及凹面反射光栅。
光栅是一种多狭缝元件，光栅光谱的产生是单狭缝衍射和多狭缝干涉两者联合作用的结果。
单狭缝衍射决定谱线的强度分布，多狭缝干涉决定谱线出现的位置。
图10－14是平面反射光栅的一段垂直于刻线截面的示意图.其色散作用可用光栅公式表示：式中α、Q分别为入射角和衍射角，d为光栅常数，n为光谱级次，n＝0，±1，±2，…。
α角规定为正值，如果Q角与α角在光栅法线同侧，α角取正值，异侧取负值。
当n＝0时，即零级光谱，衍射角与波长无关，即无分光作用。
在n＞0的相邻光谱级次之间，会产生不同级次光谱的重叠，可采用滤光片或低色散的棱镜分级器等方法消除。
★ 光栅的光学特性光栅的光学特性有色散率、分辨率及闪耀三个方面表示。
∙色散率当入射角α不变时，光栅的角色散率可用光栅公式微分求得：当Q很小且变化不大时，可以认为cosQ＝1。
则，即光栅的角色散率只决定于光栅常数d及光谱级数n，可以认为是常数，不随波长而变，这样的光谱在长波及短波的各波段时波长间隔是一样的，称为“均排光谱”。
这是光栅优于棱镜的一个方面。
在实际工作中常用线色散率表示，对于平面光栅来说，线色散率为：（凹面光栅的线色散率为，r为曲率半径）式中f为会聚透镜的焦距。
由于则cosQ＝1（Q≈6o）则。
∙分辨率光栅的分辨率R为光谱级次与光栅刻痕总数N（光栅的宽度与单位长度的刻痕的乘积），即例如，对于一块宽度为50mm，单位长度刻痕数为1200条/mm的光栅，在第一级光谱中（n ＝1），它的分辨率为：R＝nN＝1×50×1200＝6×104可见光栅的分辨率比棱镜高得多，这是光栅优于棱镜的又一方面。
光栅的宽度越大，单位长度的刻痕数越多，分辨率就越大。
闪耀特性在平面光栅中，不同级次光谱的能量分布是不均匀的。
未经色散的零级（n＝0）光谱的能量最大，按正负一级、二级光谱等逐级减弱。