2014数理统计复习资料
2014年自考 概率论与数理统计串讲讲义 第二章 随机变量及其概率分布
第二章 随机变量及其概率分布1． 离散型随机变量()01k K K KP X x p p ==≥⎧⎪⎨=⎪⎩∑ 例1 设 ，则3.02.05.01=--=c2．常见离散型随机变量（1）0—1分布：设X ～),1(p B ，则应用背景：一次抽样中，某事件A 发生的次数X ～),1(p B ，其中EX X P A P p ====)1()(例2 设某射手的命中率为p ，X 为其一次射击中击中目标的次数，则X ～),1(p B（2）二项分布：设X ～),(p n B ，则()(1),0,1,2,,k k n k n P X k C p p k n -==-=应用背景：n 次独立重复抽样中某事件A 发生的次数X ～),(p n B ，其中()p P A =为事件A 在一次抽样中发生的概率。
例３ 某射手的命中率为0.8，X 为其5次射击中命中目标的次数，则X 取的可能值为5,,1,0 ，52()0.80.2k k k P X k C -==，即X ～)8.0,5(B记住：若X ～),(p n B ，则np EX =,)1(p np DX -=（3）泊松（Poisson ）分布 若(),0,1,2,!KP X k e k k λλ-===则称X 服从参数λ的泊松分布，且DX EX ==λ，记X ～)(λB ，0>λ应用背景：偶然性事件发生的次数X 一般服从某个参数的泊松分布，如某地的降雨的次数，车祸发生的次数等等。
另外，当Y ～),(p n B ，且n 很大，P 很小时，令np =λ，则()!kP Y k e k λλ-=≈例4 一个工厂生产的产品中的次品率0.005，任取1000件，计算解：设X 表任取的1000件产品中的次品数，则X ～)005.0,100(B ，由于n 很大，p 很小，令5==np λ则（1）55551506151!15!051)1()0(1)2(------=--=--≈=-=-=≥e e e e e X P X P X P （2）5505(5)!kk P X e k -=≤≈∑3．随机变量的分布函数：X 的分布函数为)()(x X P X F ≤=，+∞<<∞-x)(x F 的性质：①1)(0≤≤x F②若21x x <，则0)()(12≥-x F x F③1)(,0)(=+∞=-∞F F④)()(b F b X P =≤，)(1)(),()()(b F b X P a f b F b X a P -=>-=≤<例5 设X 的分布函数⎩⎨⎧≤>+=-0,00,)(x x be a x F x λ，其中0>λ，则______=a b=______. 解：由1)(=+∞F 知1=a （因为a be a F x x =+=+∞-+∞→)(lim )(λ）由0)(=-∞F ，及题设0≤x 时0)(=x F ，故0)1()()(lim 0=+=+=-→+b be a x F x x λ综上有⎩⎨⎧≤>-=-0,00,1)(x x e x F x λ，即1,1-==b a例6 设X 的分布函数⎪⎩⎪⎨⎧≥<≤<=e x e x x x x F ,11,ln 1,0)(求 )5.22(),30(),2(≤<≤<≤X P X P X P解：2ln )2()2(==≤F X P101)0()3()30(=-=-=≤<F F X P25.1ln 2ln 5.2ln )2()5.2()5.22(=-=-=≤<F F X P4． 连续型随机变量若((,))()b a P X a b f x dx ∈=⎰，其中b a <任意，则称X 为连续型随机变量。
概率论与数理统计期末考试复习资料
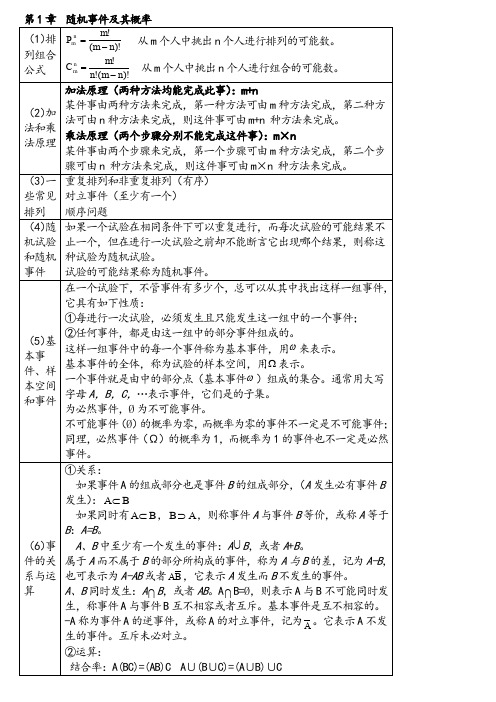
F (x) x f (x)dx ，
则称 X 为连续型随机变量。f (x) 称为 X 的概率密度函数或密度函 数，简称概率密度。 密度函数具有下面 4 个性质： 1° f (x) 0 。
2° f (x)dx 1。
X
| x1, x2,, xk, 。
P( X xk) p1, p2,, pk,
显然分布律应满足下列条件：
（2）连 续型随 机变量 的分布 密度
（3）离 散与连 续型随 机变量 的关系 （4）分 布函数
（5）八 大分布
（1） pk 0 ，k 1,2,， （2） pk 1。 k 1
ba
f
(x)
b
1
a
,
0,
a≤x≤b
其他，
则称随机变量 X 在[a，b]上服从均匀分布，记为 X~U(a，b)。
分布函数为
0，
xa, ba
x<a， a≤x≤b
x
F (x) f (x)dx
1，
x>b。
当 a≤x1<x2≤b 时，X 落在区间（x1, x2 ）内的概率为
P( A)
条件概
下，事件 B 发生的条件概率，记为P(B / A) P(AB) 。
P( A)
率
条件概率是概率的一种，所有概率的性质都适合于条件概率。
例如 P(Ω/B)=1P( B /A)=1-P(B/A)
（13） 乘法公式：P(AB) P(A)P(B / A)
乘法公 更一般地，对事件 A1，A2，…An，若 P(A1A2…An-1)>0，则有
2013-2014概率论与数理统计期末复习试题
概率论与数理统计期末复习题一一、填空题（每空2分，共20分）1、设X 为连续型随机变量，则P{X=1}=( ).2、袋中有50个球,其编号从01到50,从中任取一球,其编号中有数字4的概率为( ).3、若随机变量X 的分布律为P{X=k}=C(2/3)k,k=1,2,3,4,则C=( ). 4、设X 服从N （1，4）分布，Y 服从P(1)分布，且X 与Y 独立，则 E （XY+1-Y ）=（ ） ，D （2Y-X+1）=（ ）.5、已知随机变量X ～N(μ,σ2),(X-5)/4服从N(0,1),则μ=( );σ=( ). 6、已知随机变量(X,Y)的分布律为：且X 与Y 相互独立。
则A=( ),B=( ).7、设X 1,X 2,…,X n 是取自均匀分布U[0,θ]的一个样本，其中θ>0,n x x x ,...,,21是一组观察值，则θ的极大似然估计量为( ). 二、计算题（每题12分，共48分）1、钥匙掉了,落在宿舍中的概率为40%,这种情况下找到的概率为0.9; 落在教室里的概率为35%,这种情况下找到的概率为0.3; 落在路上的概率为25%,这种情况下找到的概率为0.1,求(1)找到钥匙的概率;(2)若钥匙已经找到,则该钥匙落在教室里的概率. 2、已知随机变量X 的概率密度为其中λ>0为已知参数.(1)求常数A; (2)求P{-1＜X ＜1/λ)}; (3)F(1). 3、设随机变量X 的分布律为且X X Y 22+=，求(1)()E X ; (2)()E Y ; (3))(X D . 4、若X ～N(μ,σ2),求μ, σ2的矩估计.⎪⎩⎪⎨⎧<≥=-000)(2x x e A x f x λλ三、解答题（12分）设某次考试的考生的成绩X 服从正态分布，从中随机地抽取36位考生的成绩，算得平均成绩为66.5分,标准差为15分,问在显著性水平0.05下,是否可以认为在这次考试中全体考生的平均成绩为70分?四、综合题（每小题4分，共20分） 设二维随机变量),(Y X 的联合密度函数为：32,01,01(,)0,x ce y x y f x y ⎧≤≤≤≤=⎨⎩其它试求: )1( 常数C ；)2(()X f x , )(y f Y ；)3( X 与Y 是否相互独立？)4( )(X E ,)(Y E ,)(XY E ； )5( )(X D ,)(Y D . 附：Φ（1.96）=0.975； Φ（1）=0.84； Φ（2）=0.9772t 0.05(9)= 1.8331 ; t 0.025(9)=2.262 ; 8595.1)8(05.0=t ， 306.2)8(025.0=t t 0.05(36)= 1.6883 ; t 0.025(36)=2.0281 ; 0.05(35) 1.6896t =， 0.025(35) 2.0301t =概率论与数理统计期末复习试题一参考答案一、填空题（每空2分，共20分）1、0 ；2、14/50 或7/25 ；3、81/130 ；4、1，17 ；5、5，4 ；6、0.35，0.35 ；7、X (n) 二、计算题（每题12分，共48分）1、解：(1)以A 1,A 2,A 3分别记钥匙落在宿舍中、落在教室里、落在路上，以B 记找到钥匙.则P(A 1)=0.4,P(A 2)=0.35,P(A 3)=0.25, P(B| A 1)=0.9 ,P(B| A 2)=0.3,P(B| A 3)=0.1 所以,49.01.025.03.035.09.04.0)|()()(31=⨯+⨯+⨯==∑=ii iA B P A P B P (6)(2)21.049.0/)3.035.0()|(2=⨯=B A P ………………………………12 2、解：（1）由归一性：λλλλλλ/1,|)(102==-===∞+--+∞+∞∞-⎰⎰A A e A dx e A dx x f x x 所以………………………4 （2）⎰=-==<<--λλλλ/1036.0/11}/11{e dx e X P x (8)（3）⎰---==11)1(λλλe dx e F x (12)3、解：（1）14.023.012.001.01)(=⨯+⨯+⨯+⨯-=X E ………………………4 （2）24.043.012.001.01)(2=⨯+⨯+⨯+⨯=X E422)(2)()2()(22=+=+=+=X E X E X X E Y E (8)（3）112)]([)()(22=-=-=X E X E X D (12)4、解：（1）E(X)=μ 令μ=-X 所以μ的矩估计为-Λ=X μ (6)（2）D(X)=E(X 2)-[E(X)]2又E(X 2)=∑=n i i X n 121D(X)= ∑=n i i X n 121--X =212)(1σ=-∑=-n i i X X n所以σ2的矩估计为∑=-Λ-=ni i X X n 122)(1σ………………………12 三、解答题（12分）解：提出假设检验问题：H 0: μ=70, H 1 ：μ≠70,nS X t /70-=-～t(n-1),其中n=36,-x =66.5,s=15,α=0.05,t α/2(n-1)=t 0.025(35)=2.03 (6)03.24.136/15|705.66|||<=-=t (12)所以,接受H 0,在显著性水平0.05下,可认为在这次考试中全体考生的平均成绩为70分. 四、综合题（每小题4分，共20分） 解：(1))1(9|31|3113103103101010102323-=⋅⋅=⋅==⎰⎰⎰⎰e c y e c dy y dx e c dxdy y ce x x x 所以,c=9/(e 3-1) (4)(2)0)(1319)(,103323103=-=-=≤≤⎰x f x e e dy y e e x f x X xx X 为其它情况时，当当所以,333,01()10,xX e x f x e ⎧≤≤⎪=-⎨⎪⎩其它 (2)同理,23,01()0,Y y y f y ⎧≤≤=⎨⎩其它 (4)(3)因为:32333,01,01()()(,)10,x X Y e y x y f x f y f x y e ⎧⋅≤≤≤≤⎪==-⎨⎪⎩其它所以,X 与Y 相互独立. ………………………4 (4)1133330013130303331111(|)1213(1)x xx x EX x e dx xde e e y e e dx e e e =⋅=--=⋅--+=-⎰⎰⎰………………………2 124100333|44EY y y dx y =⋅==⎰ (3)3321()4(1)e E XY EX EY e +=⋅=- ………………………4 (5) 22()DX EX EX =-11223231303300133130303331|21112(|)13529(1)x x xx x EX x e dy x e e xdx e e e xe e dx e e e ⎡⎤=⋅=⋅-⋅⎢⎥⎣⎦--⎡⎤=--⎢⎥-⎣⎦-=-⎰⎰⎰………………………2 ∴3323326332521(21)9(1)9(1)1119(1)e DX e e e e e e -=-+---+=- (3)22()DY EY EY =-12225010333|55EY y y dy y =⋅==⎰ ∴ 2333()5480DY =-= (4)概率论与数理统计期末复习题二一、计算题（每题10分，共70分）1、设P （A ）=1/3，P （B ）=1/4，P （A ∪B ）=1/2.求P （AB ）、P （A-B ）.2、设有甲乙两袋，甲袋中装有3只白球、2只红球，乙袋中装有2只白球、3只红球.今从甲袋中任取一球放入乙袋，再从乙袋中任取两球，问两球都为白球的概率是多少？3、已知随机变量X 的密度函数为01()2120xx p x Axx <≤⎧⎪=-<≤⎨⎪⎩其它(1)求A.（2）X 的分布函数)(x F .4、若X ，Y 为相互独立的分别服从]10[，上均匀分布的随机变量，试求Z X Y =+的分布密度函数.5、某镇年满18岁的居民中20%受过高等教育.今从中有放回地抽取1600人的随机样本，求样本中19%和21%之间的人受过高等教育的概率.6、某单位职工每天的医疗费服从正态分布),(2σμN ，现抽查了25天，得元，30=S 元，求职工每天医疗费均值μ的双侧0.95置信区间. 7、设总体X 的密度函数为⎩⎨⎧<<=-otherx x x f ,010,)(1θθ 其中θ是未知参数，且0>θ。
2014概率论与数理统计9-数理统计4 [兼容模式]
![2014概率论与数理统计9-数理统计4 [兼容模式]](https://img.taocdn.com/s3/m/3168f33e4b35eefdc8d333d1.png)
数学基础课许述文副教授假设检验雷达信号处理国家重点实验室许述文作品前言FOREWORD统计推断的另一类重要问题是假设检验问题。
在总体的分布函数完全未知或只知其形式、但不知其参数的情况，为了推断总体的某些未知特性，提出某些关于总体的假设。
例如，提出总体服从泊松分布的假设，又如，对于正态总体提出数学期望等于μ的假设等。
我们要根据样本对所提出的假设作出是接受还是拒绝的决策。
假设检验是作出这一决策的过程。
LOGO过渡页TRANSITION PAGE第一部分假设检验LOGO假设检验根据样本的信息检验关于总体的某个假设是否正确。
参数假设检验非参数假设检验LOGO参数假设检验让我们先看一个例子：罐装可乐的容量按标准为355毫升。
生产流水线上罐装可乐不断地封装，然后装箱外运。
怎么知道这批罐装可乐的容量是否合格呢？LOGO通常的办法是进行抽样检查：如每隔1小时，抽查5罐，得到一个容量为5的子样（x1，…，x5）。
每隔一定时间，抽查若干罐。
如何根据这些值来判断生产是否正常？LOGO在正常生产条件下，由于种种随机因素的影响，每罐可乐的容量应在355毫升上下波动。
这些因素中没有哪一个占有特殊重要的地位。
因此，根据中心极限定理，假定每罐容量服从正态分布是合理的。
μσX N(,)～2LOGOLOGO要检验的假设：0μμ=H 0：（= 355）0μ对立假设：H 1：0μμ≠称H 0为原假设（零假设）；称H 1为备择假设（对立假设）。
在实际工作中，往往把不轻易否定的命题作为原假设。
LOGO如何判断原假设H 0是否成立？X 355-∴不应太大X μ∵为的无偏估计X 355-考虑对差异作定量的分析，以确定其性质：1.差异可能是由抽样的随机性引起的，称为“抽样误差”或随机误差LOGO X 355 若较大合理的界限在何处？应由什么原则来确定？认为这个差异反映了事物的本质差别，即反映了生产已不正常。
这种差异称作“系统误差”2.LOGO带概率性质的反证法小概率事件在一次试验中基本上不会发生。
2014年自考 概率论与数理统计 冲刺串讲 考前老师划重点
第一章 随机事件及其概率1． 事件的关系与运算必然事件：Ω—随机试验全部结果构成的集合。
不可能事件：φ一般事件A ：A φ⊂⊂Ω若A 、B 为两事件 若B A ⊂，则其蕴含：“A 发生导致B 发生”。
若φ=⋂=B A AB ，这表示A 发生时，B 必不发生，反之亦然。
若 A-B=A ，则AB=φ；若 AB=A ，则B A ⊂；若A ∪B ＝A ，则B ⊂A 。
若n A A A ,,21为n 个事件，由它们的运算可产生诸多新事件，如1111,,n n n i i i i i i i i A A A A ∞=====等等。
例1 事件n i i A 1=发生等于“n A A A ,,21至少有1个发生”。
2．常用概率公式（1）1)(≤≤A P O ，1)(=ΩP ，0)(=φP（2）若B A ⊂，则)()(B P A P ≤（3）)()()()(AB P B P A P B A P -+=⋃；当φ=AB ，则)()()(B P A P B A P +=⋃)()()()()()()()(ABC P BC P AC P AB P C P B P A P C B A P +---++=⋃⋃（4）)(1)(A P A P -=（5）)()()(AB P A P B A P -=-（6）若n A A A ,,21两两互不相容，则∑===ni i n i i A P A P 11)()(（7）若n A A A ,,21相互独立，则 )()()()(211n ni i A P A P A P A P ==)()()()(211n n i i A P A P A P A P ==例2 设1.0)(,4.0)(,2.0)(===AB P B P A P 则5.0)()()(1)(1)(=+--=⋃-=⋃AB P B P A P B A P B A P1.0)()()()(=-=-=AB P A P B A P B A P3．古典概型古典概型：当随机试验的结果为有限个且诸结果等可能发生时，任一事件A 的概率为的样本点个数的样本点个数Ω==A n r A P )( 例3 从五个球（其中两个白球、三个红球）中任取两球，设A ：取到两个白球；B ：一白一红球，求)(),(B P A P（1）无放回抽样：101)(2522==C C A P 53)(251312==C C C B P （2）有放回抽样：每次有放回的取一球，连取两次2)52()(=A P 1223()()()55P B C = ［注］：若设X 为两次有放回取球中取到白球数，则X ～)52,2(B ，从而12122)521()52()2()(--===C X P A P4．条件概率（1）若0)(>B P ，则)()()(B P AB P B A P =，其中A 为任一事件。
数理统计复习资料
复习资料（资料总结，仅供参考）判断题1.研究人员测量了100例患者外周血的红细胞数，所得资料为计数资料。
X 2.统计分析包括统计描述和统计推断。
3.计量资料、计数资料和等级资料可根据分析需要相互转化。
4.均数总是大于中位数。
X 5.均数总是比标准差大。
X 6.变异系数的量纲和原量纲相同。
X 7.样本均数大时，标准差也一定会大。
X 8.样本量增大时，极差会增大。
9.若两样本均数比较的假设检验结果P 值远远小于0.01，则说明差异非常大。
X 10.对同一参数的估计，99%可信区间比90%可信区间好。
X 11.均数的标准误越小，则对总体均数的估计越精密。
12. 四个样本率做比较，2)3(05.02χχ> ，可认为各总体率均不相等。
X13.统计资料符合参数检验应用条件，但数据量很大，可以采用非参数方法进行初步分析。
14.对同一资料和同一研究目的，应用参数检验方法，所得出的结论更为可靠。
X 15.等级资料差别的假设检验只能采用秩和检验，而不能采用列联表χ2检验等检验方法X 。
16.非参数统计方法是用于检验总体中位数、极差等总体参数的方法。
X 17.剩余平方和SS 剩1=SS 剩2，则r 1必然等于r 2。
X 18.直线回归反映两变量间的依存关系，而直线相关反映两变量间的相互直线关系。
19.两变量关系越密切r 值越大。
X 20.一个绘制合理的统计图可直观的反映事物间的正确数量关系。
21.在一个统计表中，如果某处数字为“0”，就填“0”，如果数字暂缺则填“…”，如果该处没 有数字，则不填。
X 22.备注不是统计表的必要组成部分，不必设专栏，必要时，可在表的下方加以说明。
23.散点图是描写原始观察值在各个对比组分布情况的图形，常用于例数不是很多的间断性分组资料的比较。
24.百分条图表示事物各组成部分在总体中所占比重，以长条的全长为100%，按资料的原始顺序依次进行绘制，其他置于最后。
X 25.用元参钩藤汤治疗80名高血压患者，服用半月后比服用前血压下降了2.8kPa ，故认为该药有效（ X ）。
2013~2014年全国自考概率论与数理统计试题及答案要点
全国2013年1月高等教育自学考试概率论与数理统计(经管类)试题一、单项选择题(本大题共10小题，每小题2分，共20分)二、填空题(本大题共15小题，每小题2分，共30分)三、计算题(本大题共2小题，每小题8分，共16分)四、综合题(本大题共2小题，每小题12分，共24分)五、应用题(10分)全国2013年1月高等教育自学考试 概率论与数理统计(经管类)答案1、本题考查的是和事件的概率公式，答案为C.2、解：()()(|)1()()P B AB P AB P B AB P AB P AB ⋂===()()()0.50.15(|)0.5()()1()0.7P BA P B P AB P B A P B P A P A --=====- ()()0.15(|)0.3()()()0.5P B AB P AB P AB B P A P B P B ⋂=====()()(|)1()()P A AB P AB P A AB P AB P AB ⋂=== ，故选B.3、解：本题考查的是分布函数的性质。
由()1F +∞=可知，A 、B 不能作为分布函数。
再由分布函数的单调不减性，可知D 不是分布函数。
所以答案为C 。
4、解：选A 。
{||2}{2}{2}1{2}{2}1(2)(2)1(2)1(2)22(2)P X P X P X P X P X >=>+<-=-≤+<-=-Φ+Φ-=-Φ+-Φ=-Φ 5、解：因为(2)0.20.16P Y c ===+，所以0.04c =又(2)10.80.20.02P X c d ==-==++，所以10.020.040.14d =--= ，故选D 。
6、解：若~()X P λ，则()()E X D X λ==，故 D 。
7、解：由方差的性质和二项分布的期望和方差：1512(1)()()3695276633D X Y D X D Y -+=+=⨯⨯+⨯⨯=+= ，选A8、解：由切比雪夫不等式2(){|()|}1D X P X E X εε-<>-，可得21600{78008200}{|8000|200}10.96200P X P X <<=-<>-= ，选C 。
2014年自考 概率论与数理统计串讲讲义 第四章 随机变量的数字特征
EX = (−1) × + 1 ×
1 2
［注］ ： DX =
EX 2 − ( EX ) 2 是重要常用公式
1 + x, − 1 ≤ x < 0 例 5 设随机变量 X 具有概率密度 f ( x) = 1 − x, 0 ≤ x ≤ 1 ，求 DX 0, 其他
解：因 f ( x) 是分段函数，故求 EX , EX 时也要随之分段积分
2
EX = ∫ xf ( x)dx = ∫ x(1 + x)dx + ∫ x(1 − x)dx = 0
−∞ −1
+∞
0
1
0
EX 2 = ∫ x 2 f ( x)dx = ∫ x 2 (1 + x)dx + ∫ x 2 (1 − x)dx =
−∞ −1
0
+∞
0
1
1 6
于是 DX =
E ( X 2 ) − ( EX ) 2 =
=
0
2 3
2． 单个随机变量函数的期望
设 X 为随机变量， y =
g ( x) 是普通函数，则 Y = g ( X ) 是随机变量，且
∑ g ( xi ) p ( X = xi ), 当X为离散型 * Eg ( X ) = i+∞ ∫ g ( x) f ( x)dx, 当X为连续型，且X具有密度f ( x) −∞
例6
设 ( X , Y) 分布律为
，Z =
g ( X , Y) = XY
则 E ( XY) = (0 × 0) P00 + (0 × 1) P01 + (1 × 0) P10 + (1 × 1) P11 = (1 × 1) P11 = 1 ×
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单因子方差分析
例4.1.1 在饲料养鸡增肥的研究中，某研究 所提出三种饲料配方：A1是以鱼粉为主的饲 料，A2是以槐树粉为主的饲料，A3是以苜蓿 粉为主的饲料。选取 24 只相似的雏鸡随机 均分为三组，每组各喂一种饲料，60天后观 察它们的重量。试验结果如下表所示, 比较 三种饲料的效果是否有显著差异？
FZ (z) 1 P( X1 z, X 2 z, , X n z)
1 P( X1 z)P( X 2 z) P(X n z)
1
n
(1
P( X
i
z))
0
nz
z0
i 1
1 e z 0
fZ
(
z)
n
0
nz
e
z0 z0
即
Z ~ En
E(Z)
n
E(nZ )
故 nZ 是 的无偏估计量.
例3.3.2 某厂生产的产品优质品率一直保持在 40%，近期对该厂生产的该类产品抽检 20
件，其中优质品7件，在 0.05下能否认为
优质品率仍保持在40%？
解：以p 表示优质品率，x 表示20件产品中的优质
品件数，则 x ~ b20, p， 待检验的假设为
H0 : p 0.4 vs H1 : p 0.4
(3)
选取枢轴量
K
5S 2
2
~ 2 (5)
s2 0.051.
查表得
2 0.975
(5)
12.833,
2 0.025
(5)
0.831
由公式 (4) 得 的置信区间为
( 5 s2 , 5 s2 ) ( 0.0199, 0.3069 )
2 0.975
(5)
2 0.025
(5)
3.3.2 比例的检验
例4 设总体 X 的密度函数为
f
(x; )
1
x
e
x 0,
0 为常数
0
x0
( X1, X 2 , , X n ) 为 X 的一个样本
证明 X 与 n min{ X1, X 2 , , X n}都是 的无偏
估计量
证
X
~
E1
E(X )
故 E(X ) E(X )
X 是 的无偏估计量.
令
Z min{ X1, X 2 , , X n}
3.75
2
4
6
4
2
2
由于 2 3未.7落5 入拒绝域，故接受原假设，
没有理由认为转盘不均匀。
在分布拟合检验中使用p 值也是方便的。
本例中，以T 记服从 2(5)的随机变量，则使用
统计软件可以算出
p P T 3.75 0.5859.
这个p 值就反映了数据与假设的分布拟合程度的 高低，p 值越大，拟合越好。
表4.1.1 鸡饲料试验数据
饲料A
鸡 重（克）
A1 1073 1009 1060 1001 1002 1012 1009 1028 A2 1107 1092 990 1109 1090 1074 1122 1001
A3 1093 1029 1080 1021 1022 1032 1029 1048
例1 某工厂生产一批滚珠, 其直径 X 服从正态分
布N( 2), 现从某天的产品中随机抽取6件,测得
直径为
15.1 , 14.8 , 15.2 , 14.9 , 14.6 , 15.1
(1) 若 2=0.06, 求 的置信度为95%的 置信区间; (2) 若 2未知,求 的置信度为95%的置信区间; (3) 求方差 2的置信度为95%的置信区间.
附带指出，该拒绝域的显著性水平实际上不是 0.05，而是0.0160+0.021=0.0370 。 由于观测值没有落入拒绝域，故接受原假设。
§3.4 分布拟合检验
例3.4.1 为募集社会福利基金，某地方政府发 行福利彩票，中彩者用摇大转盘的方法确定 最后中奖金额。大转盘均分为20份，其中金 额为5万、10万、20万、30万、50万、100万 的分别占2份、4份、6份、4份、2份、2份。 假定大转盘是均匀的，则每一点朝下是等可 能的，于是摇出各个奖项的概率如下：
解：这是一个典型的分布拟合优度检验，总体 共有6类，其发生概率分别为0.1、0.2、0.3、 0.2、0.1和0.1，这里k=6，检验拒绝域为:
2
2 1
5
,
2 0.95
5
11.07.
若取 =0.05，则查附表3知
由本例数据可以算出
2 =
2 22 6 42 6 62 3 42 3 22 0 22
A3 93 29 80 21 22 32 29 48 354 125316 20984 1133 505177 91363
解 (1) X ~ N (, 0.06) 即 N (,0.01)
6
X ~ N (0,1)
0.1
z1
2
z0.975
1.96
由给定数据算得
x
1 6
6 i1
xi
14.95
由公式 (1) 得 的置信区间为
( 14.95 1.96 0.1, 14.95 1.96 0.1 ) ( 14.75, 15.15 )
额度 5万 10万 20万 30万 50万 100万
概率 0.1 0.2 0.3 0.2 0.1 0.1
现20人参加摇奖，摇得5万、10万、20万、30万、 50万和100万的人数分别为2、6、6、3、3、0， 由于没有一个人摇到100万，于是有人怀疑大转 盘是不均匀的，那么该怀疑是否成立呢？这就需 要对转盘的均匀性作检验。
(2)
取
T
X S
~
t (5)
查表得 t0.975 (5) 2.5706
6
由给定数据算得 x 14.95
s2
1 5
(
6 i 1
xi2
6x2)
0.051.
s 0.226
由公式 (2) 得 的置信区间为
(x
s 6
t0.975
(5),
x
s 6
t0.975(5)Fra bibliotek)(14.71, 15.187 )
拒绝域为
W x c1 或 x c2
下求c1与c2: 由于
P x 3 0.0160 0.025 P x 4 0.0510,
故取 c1=3，又因为
P x 11 0.0565 0.025 P x 12 0.0210,
从而c2=12，拒绝域为 W x 3或 x 12
例4.1.2 采用例4.1.1的数据，将原始数据减去1000，
列表给出计算过程：
表4.1.4 例4.1.2的计算表
水 平
数据（原始数据-1000）
m
Ti
2
Ti
yi2j
j 1
A1 73 9 60 1 2 12 9 28 194 37636 10024
A2 107 92 -10 109 90 74 122 1 585 342225 60355