概率论复习题PPT精选文档
合集下载
概率论部分总复习练习题最终版.ppt

2
PB P Ai P B Ai
i 1
0.5 0.05 0.5 0.0025 0.0265
P
A1 B
P A1 PB PB
A1
0.5 0.95 1 0.02625
0.4&8780&
20 41
五、设随机变量 X 的分布函数为
0
x 1
F (x) a barcsin x 1 x 1
则随机变量3X 2Y 的方差为 (D) .
(A) 8
(B) 16
(C) 28
(D) 44
5 设 X ~ N(, 2),对于任何实数 ,都有 (B) .
(A) P{X } 1 P{X }
(B) P{X } 1 P{X }
(C) X ~ N(0, 2) (D) X ~ N(, 2 2)
三、从 5 双不同的鞋子中任取 4 只,求下列事件发生的 概率:
(1) 恰有一双配对; (2) 至少有一双配对。
解:设A表示所取4只中恰有一双配对的事件; B表示所取4只中至少有一双配对的事件。
P A C15C22C24C12C12 12
C140
21
P
B
1 P
B
1
C54C12C12C12C12 C140
。
一、填空题
9 若 X ,Y 相 互 独 立 , 且 X ~ N (0,1),Y ~ N (0,1) , 则
aX bY ~ N 0,a2 b2 。
10 设随机变量 X 在(1,6)上服从均匀分布,则方程
4
x2 Xx 1 0有实根的概率是 5
。
二、选择题
1 若事件 A与B互不相容,则P A U B (A)
解:(1) (X ,Y )的联合概率密度函数为
PB P Ai P B Ai
i 1
0.5 0.05 0.5 0.0025 0.0265
P
A1 B
P A1 PB PB
A1
0.5 0.95 1 0.02625
0.4&8780&
20 41
五、设随机变量 X 的分布函数为
0
x 1
F (x) a barcsin x 1 x 1
则随机变量3X 2Y 的方差为 (D) .
(A) 8
(B) 16
(C) 28
(D) 44
5 设 X ~ N(, 2),对于任何实数 ,都有 (B) .
(A) P{X } 1 P{X }
(B) P{X } 1 P{X }
(C) X ~ N(0, 2) (D) X ~ N(, 2 2)
三、从 5 双不同的鞋子中任取 4 只,求下列事件发生的 概率:
(1) 恰有一双配对; (2) 至少有一双配对。
解:设A表示所取4只中恰有一双配对的事件; B表示所取4只中至少有一双配对的事件。
P A C15C22C24C12C12 12
C140
21
P
B
1 P
B
1
C54C12C12C12C12 C140
。
一、填空题
9 若 X ,Y 相 互 独 立 , 且 X ~ N (0,1),Y ~ N (0,1) , 则
aX bY ~ N 0,a2 b2 。
10 设随机变量 X 在(1,6)上服从均匀分布,则方程
4
x2 Xx 1 0有实根的概率是 5
。
二、选择题
1 若事件 A与B互不相容,则P A U B (A)
解:(1) (X ,Y )的联合概率密度函数为
概率论总复习ppt课件

解 令 A 灯泡能用到1000小时, B 灯泡能用到 1500小时
所求概率为
PBAP(AB) P(B)0.41
P(A) P(A) 0.8 2
2021/4/25
BA
三.全概率公式
定义
若事件组B1,…Bn,满足:
(1) (2)
B1,…Bn互不相容且P(Bi)>0,i=1,…,n
n Bi S
i 1
则称事件B1,…Bn为样本空间的一个划分
三.概率的频率定义
例2:从同一型号同一批次的反坦克弹中任抽一发反 坦克弹射击目标,观测命中情况。设A代表“命中” 这一事件,求P(A)?
1 . 事件的频率 在一组不变的条件下,重复作n次试验,记
m是n次试验中事件A发生的次数。 频率 f = m/n
2. 频率的稳定性
掷一枚均匀硬币,记录前400次掷硬币试验中 频率P*的波动情况。
离散型随机变量的概念
定义 若随机变量 X 的可能取值是有限多个或 无穷可列多个,则称 X 为离散型随机变量
描述离散型随机变量的概率特性常用它的概率 分布或分布律,即
P ( X x k ) p k ,k 1 ,2 ,
概率分布的性质
2021/4/25
p k0 ,k 1 ,2 ,
pk 1
k 1
非负性 规范性
称 X 服从参数为n, p 的二项分布,记作 X~B(n,p)
0 – 1 分布是 n = 1 的二项分布
2021/4/25
例6 设有同类型设备90台,每台工作相互独立,每台设 备发生故障的概率都是 0.01. 在通 情况下,一台设备发 生故障可由一个人独立维修,每人同时也只能维修一台 设备. 问至少要配备多少维修工人,才能保证当设备发 生故障时不能及时维修的概率小于0.01?
所求概率为
PBAP(AB) P(B)0.41
P(A) P(A) 0.8 2
2021/4/25
BA
三.全概率公式
定义
若事件组B1,…Bn,满足:
(1) (2)
B1,…Bn互不相容且P(Bi)>0,i=1,…,n
n Bi S
i 1
则称事件B1,…Bn为样本空间的一个划分
三.概率的频率定义
例2:从同一型号同一批次的反坦克弹中任抽一发反 坦克弹射击目标,观测命中情况。设A代表“命中” 这一事件,求P(A)?
1 . 事件的频率 在一组不变的条件下,重复作n次试验,记
m是n次试验中事件A发生的次数。 频率 f = m/n
2. 频率的稳定性
掷一枚均匀硬币,记录前400次掷硬币试验中 频率P*的波动情况。
离散型随机变量的概念
定义 若随机变量 X 的可能取值是有限多个或 无穷可列多个,则称 X 为离散型随机变量
描述离散型随机变量的概率特性常用它的概率 分布或分布律,即
P ( X x k ) p k ,k 1 ,2 ,
概率分布的性质
2021/4/25
p k0 ,k 1 ,2 ,
pk 1
k 1
非负性 规范性
称 X 服从参数为n, p 的二项分布,记作 X~B(n,p)
0 – 1 分布是 n = 1 的二项分布
2021/4/25
例6 设有同类型设备90台,每台工作相互独立,每台设 备发生故障的概率都是 0.01. 在通 情况下,一台设备发 生故障可由一个人独立维修,每人同时也只能维修一台 设备. 问至少要配备多少维修工人,才能保证当设备发 生故障时不能及时维修的概率小于0.01?
概率论与数理统计期末复习PPT课件

P(B | A) P(B | A); (3)当0 P( A) 1, 0 P(B) 1时,
P(B | A) P(B| A) 1
第11页/共50页
2) 若事件A和B相互独立,则 (1) 事件A与事件B也相互独立 (2)事件 A与事件B也相互独立; (3) 事件A与事件B也相互独立.
n
3)若A1, A2 , An相互独立,则P A1, A2 An P Ai i 1
第1页/共50页
2.概率的几何定义
设样本空间是一个有限区域。若样本点落在
内的任何区域G中的事件A的概率与区域G的测度
(或长度、或面积、或体积等)成正比,
则区域内任意一点落在区域G的概率为区域G的
测度与区域的测度的比值,即
P(
A)
G的测度 的测度
.
第2页/共50页
3.概率的公理化定义
设E是一个随机试验,为它的样本空间,
x
4 F (x)为右连续函数,即对任意的实数x, 有F (x 0) F (x).
反之, 具有以上四个性质的函数, 一定是某个随机变量的分布函数.
二、离散型随机变量
第24页/共50页
定义 设X是一个离散型随机变量,它可
能取值为 x1, x2 ,, x并k ,且取, 各个值的对应概
率为
p1, p即2 ,, pk ,,
(A)P(A | B) P(A | B) (B)P(A | B) P(A | B)
(C)P(AB) P(A)P(B)
3.计算与证明题
(D)P(AB) P(A)P(B)
(1)设A, B是任意两个随机事件,其中A的概率
不等于0和1,证明: P(B | A) P(B | A)是随机 事件A与B独立的充要条件.
P(B | A) P(B| A) 1
第11页/共50页
2) 若事件A和B相互独立,则 (1) 事件A与事件B也相互独立 (2)事件 A与事件B也相互独立; (3) 事件A与事件B也相互独立.
n
3)若A1, A2 , An相互独立,则P A1, A2 An P Ai i 1
第1页/共50页
2.概率的几何定义
设样本空间是一个有限区域。若样本点落在
内的任何区域G中的事件A的概率与区域G的测度
(或长度、或面积、或体积等)成正比,
则区域内任意一点落在区域G的概率为区域G的
测度与区域的测度的比值,即
P(
A)
G的测度 的测度
.
第2页/共50页
3.概率的公理化定义
设E是一个随机试验,为它的样本空间,
x
4 F (x)为右连续函数,即对任意的实数x, 有F (x 0) F (x).
反之, 具有以上四个性质的函数, 一定是某个随机变量的分布函数.
二、离散型随机变量
第24页/共50页
定义 设X是一个离散型随机变量,它可
能取值为 x1, x2 ,, x并k ,且取, 各个值的对应概
率为
p1, p即2 ,, pk ,,
(A)P(A | B) P(A | B) (B)P(A | B) P(A | B)
(C)P(AB) P(A)P(B)
3.计算与证明题
(D)P(AB) P(A)P(B)
(1)设A, B是任意两个随机事件,其中A的概率
不等于0和1,证明: P(B | A) P(B | A)是随机 事件A与B独立的充要条件.
概率论期末复习-精PPT文档51页

谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
概率论期末复习-精
21、没有人陪你走一辈子,所以你要 适应孤 独,没 有人会 帮你一 辈子, 所以你 要奋斗 一生。 22、当眼泪流尽的时候,留下的应该 是坚强 。 23、要改变命运,首先改变自己。
24、勇气很有理由被当作人类德性之 首,因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿. 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ,它只 是让人 们的脚 中 华 之 崛起而 读书。 ——周 恩来
概率论复习-PPT课件

2
4
P( ABC ) 0
A、B、C中任意两个相互独立,但A、B、C不独立.
若 n 个事件相互独立,则任意两事件相互独立,但反过来 不一定正确.
10
第二、三章 随机变量及其分布
一、随 机 变 量 及其分布函数
1. 概念
(1) 0 F ( x) 1, ( x )
2. 分布函数 F ( x) P( X x)
x x
1
x2
e2
2
1
t2 x
e 2 dt
2
x
X ~ N , 2 .
f x
1
x 2
e 22
2
Ox
Px1
X
x2
x2
x1
四、 随机变量函数的分布
1、离散型
2、连续型
13
1、离散型随机变量函数的分布
设随机变量X 的概率分布为:
X
x1
x2
P( X xi ) p( x1 ) p( x2 )
设A、B为独立事件,且P(A)>0,P(B)>0,
下面四个结论中,正确的是:
1. P(B|A)>0 3. P(A|B)=0
2. P(A|B)=P(A) 4. P(AB)=P(A)P(B)
7
三、多个事件的独立性 将两事件独立的定义推广到三个事件:
对于三个事件A、B、C,若
P(AB)= P(A)P(B)
2、乘法公式
P( AB) P( A)P(B | A) P(B)P( A | B)
3、全概率公式
n
P( A) P(Bi )P( A | Bi )
i 1
4、逆概率公式
P(Bi | A)
概率论复习提纲-PPT精选

基本要求:
x k x
已知分布律求分布函数 分布律与分布函数图像的关系
分布函数F(x)在x=xk( k =1,2,3,… ) 处有跳跃,其跳 跃值为pk= P{ X=xk } . 已知分布函数求概率 P { x 1 X x 2 } F ( x 2 ) F ( x 1 )
2.连续型的随机变量X和Y的相互独立性
X 和 Y 相互独立 F ( x , y ) F X ( x ) F Y ( y ) f ( x , y ) f X ( x ) f Y ( y )
P73的两个例子;P86 第18(1)题
第四章 随机变量的数字特征
一、数学期望
1. 数学期望的定义 数学期望简称为期望或均值.
互不相容事件: 若 AB ,则A 称 和 B是互不.相容
对立事件: 若 A B S 且 A B ,则 A 和 称 B 是互为 . A的对立事 A,即 件 A记 S为 A.
P25 第2题
二、概率、等可能概型
1.概率的定义: 非负性、规范性、可列可加性 2.概率的性质:
(1)P ( )0. (2)若A1,A2,,An是两两互不相,则 容有 的
P68 例1; P71 例3;P85-86 第9,13(1)题
四、相互独立的随机变量
1.离散型的随机变量X和Y的相互独立性
X 和 Y 相互独立 F ( x , y ) F X ( x ) F Y ( y )
P { X x i , Y y j } P { X x i } P { Y y j } 对(X,Y)的所有可能取值(xi, yj)都成立.
离散型随机变量的函数的分布 例 设X的分布律为 X 1 0 1 3
p k 0 .20 .30 .10 .4 求 Y=(X-2)2 的分布律. 解 Y=(X-2)2 的分布律为
概率论复习重点与习题.ppt

P{( X ,Y ) G} f ( x, y)dxdy.
G
3)掌握二维均匀分布的定义及性质; A
f
x,
y
1 A
x, y D
y
0 x, y D
B
P{( X ,Y ) G}
G
f (x,
y)dxdy
. A
4)会求边缘分布率和边缘概率密度;
D G
B
x
pi. P{X xi} pij
j
{ } p P Y y
(3) A B P(B A) P(B) P( A)
(4) P( A) 1 P( A) (5) P( A B) P( A) P(B) P( AB)
(6) P(B A) P(B) P( AB)
3)熟练运用条件概率的定义,乘法公式,全概公 式,事件的独立性及性质求概率.
(1) PA B PPABB;
n i 1
Xi,
样本方差
S2
1 n1
n
(Xi
i 1
X )2
1
n
[
n 1 i1
Xi2
nX 2 ]
样本k 阶原点矩
Ak
1 n
n i 1
Xik
k 1,2,
样本k 阶中心矩
Bk
1 n
n
(Xi
i 1
X )k
k 1,2,
结论:设 X1 , X n 为来自总体X 的一个样本,
EX m , DX s 2 ,
f x, y f X x fY y
6)会求二维随机变量函数的分布:
(1)一般情形
先求随机变量函数Z gX, Y 的分布函数FZ z,
再求随机变量函数Z gX, Y 的密度函数 f Z z FZ z,
G
3)掌握二维均匀分布的定义及性质; A
f
x,
y
1 A
x, y D
y
0 x, y D
B
P{( X ,Y ) G}
G
f (x,
y)dxdy
. A
4)会求边缘分布率和边缘概率密度;
D G
B
x
pi. P{X xi} pij
j
{ } p P Y y
(3) A B P(B A) P(B) P( A)
(4) P( A) 1 P( A) (5) P( A B) P( A) P(B) P( AB)
(6) P(B A) P(B) P( AB)
3)熟练运用条件概率的定义,乘法公式,全概公 式,事件的独立性及性质求概率.
(1) PA B PPABB;
n i 1
Xi,
样本方差
S2
1 n1
n
(Xi
i 1
X )2
1
n
[
n 1 i1
Xi2
nX 2 ]
样本k 阶原点矩
Ak
1 n
n i 1
Xik
k 1,2,
样本k 阶中心矩
Bk
1 n
n
(Xi
i 1
X )k
k 1,2,
结论:设 X1 , X n 为来自总体X 的一个样本,
EX m , DX s 2 ,
f x, y f X x fY y
6)会求二维随机变量函数的分布:
(1)一般情形
先求随机变量函数Z gX, Y 的分布函数FZ z,
再求随机变量函数Z gX, Y 的密度函数 f Z z FZ z,
高中数学概率论复习(全)PPT
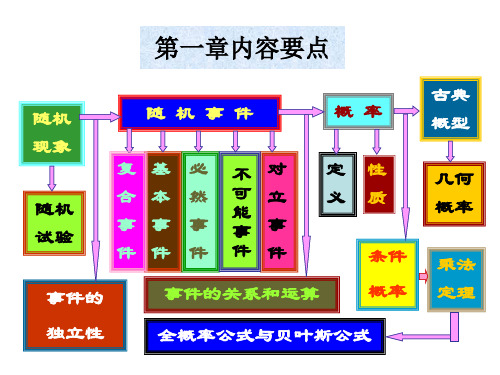
(2)有界性:对任意实数 x ,有 0 F(x) 1,且
F() lim F(x) 0 x
F() lim F(x) 1 x
(3)右连续性:F(x) 是右连续的函数,即对任
意实数 x ,有 F(x 0) F(x) . (4)对任意实数 x1, x2 (x1 x2 ) ,有 P{x1 X x2} P{X x2} P{X x1}
F (x2 ) F (x1)
【注】满足单调性、有界性和右连续性这三个性质的 函数,一定可以作为某个随机变量的分布函数.
离散型随机变量
离散型随机变量 X 的概率分布满足以下两个基本性质:
(1)非负性: pi 0 , i 1, 2, ;
(2)规范性: pi 1 . i 1
【注】满足非负性和规范性的数组 pi (i 1, 2, ) ,一 定是某个离散型随机变量的概率分布.
pij
( xi , y j )G
(4)
P{X xi} pij , i 1, 2, j 1
P{Y y j} pij , j 1, 2, i 1
二维连续型随机变量
(1)非负性 p(x, y) 0 ;
(2)规范性 p(x, y)dxdy F (, ) 1.
【注】若二元函数 p(x, y) 具有非负性和规范性,则 p(x, y) 一定是某个二维连续型随机变量的联合概率 密度函数.
定理 设随机变量 X 具有数学期望
E( X ) μ,方差 D( X ) σ 2,则对于任
(3)右连续性 F( x, y ) 分别对 x , y 右连续,即
F(x 0, y) lim F(x , y) F(x, y) 0
F(x, y 0) lim F(x, y ) F(x, y) 0
(4)非负性 对于任意的实数 x1 x2 , y1 y2 ,有
F() lim F(x) 0 x
F() lim F(x) 1 x
(3)右连续性:F(x) 是右连续的函数,即对任
意实数 x ,有 F(x 0) F(x) . (4)对任意实数 x1, x2 (x1 x2 ) ,有 P{x1 X x2} P{X x2} P{X x1}
F (x2 ) F (x1)
【注】满足单调性、有界性和右连续性这三个性质的 函数,一定可以作为某个随机变量的分布函数.
离散型随机变量
离散型随机变量 X 的概率分布满足以下两个基本性质:
(1)非负性: pi 0 , i 1, 2, ;
(2)规范性: pi 1 . i 1
【注】满足非负性和规范性的数组 pi (i 1, 2, ) ,一 定是某个离散型随机变量的概率分布.
pij
( xi , y j )G
(4)
P{X xi} pij , i 1, 2, j 1
P{Y y j} pij , j 1, 2, i 1
二维连续型随机变量
(1)非负性 p(x, y) 0 ;
(2)规范性 p(x, y)dxdy F (, ) 1.
【注】若二元函数 p(x, y) 具有非负性和规范性,则 p(x, y) 一定是某个二维连续型随机变量的联合概率 密度函数.
定理 设随机变量 X 具有数学期望
E( X ) μ,方差 D( X ) σ 2,则对于任
(3)右连续性 F( x, y ) 分别对 x , y 右连续,即
F(x 0, y) lim F(x , y) F(x, y) 0
F(x, y 0) lim F(x, y ) F(x, y) 0
(4)非负性 对于任意的实数 x1 x2 , y1 y2 ,有
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
2. 某段时间[t0,t0+t]内,t>0,证券交易所来 了k个股民的概率为 (t)k e,tk=0,1,2……,λ >0,每个来到交易所的k! 股民购买长虹股票 的概率为p,且各股民是否购买这种股票相 互独立。 (1)求此段时间内,交易所共有r个股民购 买长虹股票的概率; (2)若已知这段时间内有r个股民购买了长 虹股票,求交易所内来了m个股民的概率。
5. 某种商品一周的需求量X是一个随机变量,其概率
密度为
{ f (x)
xex,x0 0,其他
6. 假设各周的需求量相互独立,以U k 表示k周的总 需求量,
(1)求U 2 ,的U 3 概率密度; (2)求接连三周中的周最大需求量的概率密度。
10
6. 设随机变量X与Y相互独立,X的密度函数为 7. f ( x ) ,Y的分布律为
X0 1
p 1/ 1/ 22
3. 求Z=min(X,Y)的数学期望与方差。
12
3. 设随机变量X的概率密度为
ax, 0<x<2
f(x)= cx+b 2x4
0 其他
又已知E(X)=2,D(X)=2/3,求: (1)a,b,c的值; (2)随机变量Y=eX的数学期望与方差。
13
4. 设X~N(μ,σ2),Y~N(μ,σ2),且设X,Y相 互独立,求Z1=αX+βY,Z2=αX-βY的相关 系数(其中αβ是不为0的常数)。
5
2. 假设随机变量X的绝对值不大于1,
3. P(X1)1,P(X 在1)事1件,
8
4
(1X1)
4. 出现的条件下,X在(-1,1)内的任一
子区间上取值的条件概率与该子区间长度成
正比,试求:
5. (1)X的分布函数F ( x ) ;
6. (2)X的取负值的概率p。
6
3. 假设一设备开机后无故障工作的时间X服从
P ( Y a i) p i,i 1 ,2 , ,n .
8. 试求Z=X+Y的密度函数。
11
第四章
1. 设学校乘汽车到火车站的途中有3个交通岗, 设在各交通岗遇到红灯是相互独立的,其概 率均为2/5,求途中遇到红灯次数的数学期 望与方差。
2. 设相互独立的两个随机变量X,Y具有同一 分布,且X的分布律为
5. 卡车装运水泥,设每袋水泥重量X(以公斤 计)服从N(50,2.52),问最多装多少袋水泥 使总重量超过2000的概率不大于0.05。
14
6. 设随机变量X的分布密度为p(x)1ex, x
2
(1)求E(X)和D(X); (2)求X与|X|的协方差,并问X与|X|是否 相关; (3)X与|X|是否独立?为什么?
参数为1/5的指数分布,设备定时开机,出
现故障时自动关机,而在无故障的情况下工
作2个小时Y (。y ) 4. 设随机变量X 的概率密度为
{ f (x) 3x12/3, 0,其他
x1,8,
5. F ( x ) 是X的分布函数,试求随机变量Y F ( X ) 的分布函数。
概率论复习题
1
第一章
1. 假设有两箱同种零件:第一箱内装50件, 其中10件为一等品;第二箱内装30件,其 中18件一等品,现从两箱中随意挑出一箱, 然后从该箱中先后随机取出两个零件(取出 的零件均不放回),求: (1)先取出的零件是一等品的概率; (2)在先取出的零件是一等品的条件下, 第二次取出的零件仍然是一等品的概率。
P (A |B ) P (A |B )P ( C C ) P (A |B C )P ( C )
4
第二章
1. 假设一厂家生产的每台仪器,以概率0.70可 以直接出厂;以概率0.30需进一步调试,经 调试后以概率0.80可以出厂;以概率0.20定 为不合格品不能出厂。现该厂生产了 n(n2)
台仪器,假设各台仪器的生产过程相互独立, 试求: (1)全部能出厂的概率; (2)其中恰好有两件不能出厂的概率β; (3)其中至少有两件不能出厂的概率θ。
15
第五章
1. 现有一大批种子,其中良种占1/6,现从中 任取6000粒种子,试分别用切比雪夫不等 式估计和用中心极限定理计算这6000粒种 子中良种所占的比例与1/6之差的绝对值不 超过0.01的概率。
16
2. 一个食品店有三种蛋糕出售,由于售出哪一 种蛋糕是随机的,因而售出一只蛋糕的价格 是一个随机变量,它取1(元)、1.2(元)、 1.5(元)各个值的概率分别为0.3、0.2、 0.5。某天售出300只蛋糕。
7
第三章
1. 设(X,Y)的联合密度为
C xy,0x 1 ,0y 1 .
f (x, y)
2.
0,其他
3. 求:(1)常数C;(2)P(X=Y);
4.
(3)P(X < Y )。
8
2. 设连续型随机变量X,Y相互独立且服从同 一分布,证明 P (X ≤ Y)= 1/2。
3. 在10件产品中有2件一等品,7件二等品和1 件次品,现在从10件产品中无放回地抽取3 件,令X表示其中一等品数,Y表示其中二 等品数,试求:
3
3. 设一射手每次命中目标的概率为p,现对同 一目标进行若干次独立射击,直到命中目标
5次为止,则射手共射击了10次的概率为
4.
C (A150p) 5(1p)5
(B)
C94p5(1p)5
5.
C (C140)p4(1p)5
(D)
C94p4(1p)5
4. 设有三个事件A,B,C,其中P(B)>0,P(C)>0, 且事件B与事件C相互独立,证明:
(1)(X,Y)的联合分布律; (2)(X,Y)关于X和Y的边缘分布律; (3)X和Y是否相互独立? (4)在X=1的条件下Y的条件分布。
9
4. 设二维随机变量(X,Y)在区域D上服从均匀分 布,其中D={(X,Y)| 0<x<1,|y|<x},试求(X, Y)关于X和关于Y的边缘密度和条件密度。
3. (1)求这天的收入至少400(元)的概 率;
(2)求这天售出价格为1.2(元)的蛋糕多
3. 于设6a0n 只 m的n0 n,m概m!e求率n 证。
nl iman0.5
17
2. 某段时间[t0,t0+t]内,t>0,证券交易所来 了k个股民的概率为 (t)k e,tk=0,1,2……,λ >0,每个来到交易所的k! 股民购买长虹股票 的概率为p,且各股民是否购买这种股票相 互独立。 (1)求此段时间内,交易所共有r个股民购 买长虹股票的概率; (2)若已知这段时间内有r个股民购买了长 虹股票,求交易所内来了m个股民的概率。
5. 某种商品一周的需求量X是一个随机变量,其概率
密度为
{ f (x)
xex,x0 0,其他
6. 假设各周的需求量相互独立,以U k 表示k周的总 需求量,
(1)求U 2 ,的U 3 概率密度; (2)求接连三周中的周最大需求量的概率密度。
10
6. 设随机变量X与Y相互独立,X的密度函数为 7. f ( x ) ,Y的分布律为
X0 1
p 1/ 1/ 22
3. 求Z=min(X,Y)的数学期望与方差。
12
3. 设随机变量X的概率密度为
ax, 0<x<2
f(x)= cx+b 2x4
0 其他
又已知E(X)=2,D(X)=2/3,求: (1)a,b,c的值; (2)随机变量Y=eX的数学期望与方差。
13
4. 设X~N(μ,σ2),Y~N(μ,σ2),且设X,Y相 互独立,求Z1=αX+βY,Z2=αX-βY的相关 系数(其中αβ是不为0的常数)。
5
2. 假设随机变量X的绝对值不大于1,
3. P(X1)1,P(X 在1)事1件,
8
4
(1X1)
4. 出现的条件下,X在(-1,1)内的任一
子区间上取值的条件概率与该子区间长度成
正比,试求:
5. (1)X的分布函数F ( x ) ;
6. (2)X的取负值的概率p。
6
3. 假设一设备开机后无故障工作的时间X服从
P ( Y a i) p i,i 1 ,2 , ,n .
8. 试求Z=X+Y的密度函数。
11
第四章
1. 设学校乘汽车到火车站的途中有3个交通岗, 设在各交通岗遇到红灯是相互独立的,其概 率均为2/5,求途中遇到红灯次数的数学期 望与方差。
2. 设相互独立的两个随机变量X,Y具有同一 分布,且X的分布律为
5. 卡车装运水泥,设每袋水泥重量X(以公斤 计)服从N(50,2.52),问最多装多少袋水泥 使总重量超过2000的概率不大于0.05。
14
6. 设随机变量X的分布密度为p(x)1ex, x
2
(1)求E(X)和D(X); (2)求X与|X|的协方差,并问X与|X|是否 相关; (3)X与|X|是否独立?为什么?
参数为1/5的指数分布,设备定时开机,出
现故障时自动关机,而在无故障的情况下工
作2个小时Y (。y ) 4. 设随机变量X 的概率密度为
{ f (x) 3x12/3, 0,其他
x1,8,
5. F ( x ) 是X的分布函数,试求随机变量Y F ( X ) 的分布函数。
概率论复习题
1
第一章
1. 假设有两箱同种零件:第一箱内装50件, 其中10件为一等品;第二箱内装30件,其 中18件一等品,现从两箱中随意挑出一箱, 然后从该箱中先后随机取出两个零件(取出 的零件均不放回),求: (1)先取出的零件是一等品的概率; (2)在先取出的零件是一等品的条件下, 第二次取出的零件仍然是一等品的概率。
P (A |B ) P (A |B )P ( C C ) P (A |B C )P ( C )
4
第二章
1. 假设一厂家生产的每台仪器,以概率0.70可 以直接出厂;以概率0.30需进一步调试,经 调试后以概率0.80可以出厂;以概率0.20定 为不合格品不能出厂。现该厂生产了 n(n2)
台仪器,假设各台仪器的生产过程相互独立, 试求: (1)全部能出厂的概率; (2)其中恰好有两件不能出厂的概率β; (3)其中至少有两件不能出厂的概率θ。
15
第五章
1. 现有一大批种子,其中良种占1/6,现从中 任取6000粒种子,试分别用切比雪夫不等 式估计和用中心极限定理计算这6000粒种 子中良种所占的比例与1/6之差的绝对值不 超过0.01的概率。
16
2. 一个食品店有三种蛋糕出售,由于售出哪一 种蛋糕是随机的,因而售出一只蛋糕的价格 是一个随机变量,它取1(元)、1.2(元)、 1.5(元)各个值的概率分别为0.3、0.2、 0.5。某天售出300只蛋糕。
7
第三章
1. 设(X,Y)的联合密度为
C xy,0x 1 ,0y 1 .
f (x, y)
2.
0,其他
3. 求:(1)常数C;(2)P(X=Y);
4.
(3)P(X < Y )。
8
2. 设连续型随机变量X,Y相互独立且服从同 一分布,证明 P (X ≤ Y)= 1/2。
3. 在10件产品中有2件一等品,7件二等品和1 件次品,现在从10件产品中无放回地抽取3 件,令X表示其中一等品数,Y表示其中二 等品数,试求:
3
3. 设一射手每次命中目标的概率为p,现对同 一目标进行若干次独立射击,直到命中目标
5次为止,则射手共射击了10次的概率为
4.
C (A150p) 5(1p)5
(B)
C94p5(1p)5
5.
C (C140)p4(1p)5
(D)
C94p4(1p)5
4. 设有三个事件A,B,C,其中P(B)>0,P(C)>0, 且事件B与事件C相互独立,证明:
(1)(X,Y)的联合分布律; (2)(X,Y)关于X和Y的边缘分布律; (3)X和Y是否相互独立? (4)在X=1的条件下Y的条件分布。
9
4. 设二维随机变量(X,Y)在区域D上服从均匀分 布,其中D={(X,Y)| 0<x<1,|y|<x},试求(X, Y)关于X和关于Y的边缘密度和条件密度。
3. (1)求这天的收入至少400(元)的概 率;
(2)求这天售出价格为1.2(元)的蛋糕多
3. 于设6a0n 只 m的n0 n,m概m!e求率n 证。
nl iman0.5
17
