中线与中位线(培优)
九年级数学中位线知识点

九年级数学中位线知识点中位线是数学中一个重要的概念,它在统计学和几何学中都有广泛的应用。
本文将详细介绍九年级数学中位线的相关知识点,包括定义、性质和求解方法等方面。
一、定义中位线是指一条线段,它连接平面上一个三角形的一个顶点和对边中点的线段。
具体来说,对于三角形ABC,若D是边AB的中点,则CD被称为三角形ABC的中位线。
二、性质1. 中位线的长度:中位线的长度等于对边的一半。
即,在三角形ABC中,若D为边AB的中点,则CD = 1/2 AB。
2. 中位线的位置:三角形ABC的三条中位线所交于一点,我们称之为重心(G)。
重心是三角形的一个重要特殊点,它将三角形分成六个小三角形,每个小三角形的面积相等。
3. 中位线的关系:在三角形中,任意两条中位线的交点都在第三条中位线上。
这个交点将每条中位线分成两个部分,其中一个部分是另一条中位线的2倍。
三、求解方法1. 已知三角形的顶点坐标:若已知三角形的顶点坐标A(x1, y1)、B(x2, y2)、C(x3, y3),求中位线CD的方法如下:a) 计算边AB的中点坐标D,D的坐标为((x1+x2)/2,(y1+y2)/2);b) 通过点D和顶点C的坐标,可以得到中位线CD的方程;c) 求解中位线CD的相关参数,如长度、斜率等。
2. 已知三角形的边长:若已知三角形的边长a、b、c,求中位线CD的方法如下:a) 根据已知边长,利用海伦公式计算三角形的面积S;b) 根据面积S和三角形的高公式,计算三角形的高h;c) 通过三角形高的性质,计算出中位线CD的长度。
四、例题解析为了更好地理解中位线的概念和求解方法,我们将通过例题来进行解析:例题1:已知三角形ABC的坐标为A(2, 4)、B(6, 8)、C (8, 2),求中位线CD的长度。
解析:首先计算边AB的中点坐标D,D的坐标为((2+6)/2, (4+8)/2)= (4, 6)。
然后根据两点间的距离公式,计算出CD的长度:CD = √[(8-4)^2 + (2-6)^2] = √[(4^2) + (-4)^2] = √(16+16) = √32 = 4√2例题2:已知三角形的边长分别为a = 5 cm,b = 12 cm,c = 13 cm,求中位线CD的长度。
《三角形的中位线》 知识清单

《三角形的中位线》知识清单一、三角形中位线的定义连接三角形两边中点的线段叫做三角形的中位线。
需要注意的是,一个三角形共有三条中位线。
二、三角形中位线定理三角形的中位线平行于三角形的第三边,并且等于第三边的一半。
这个定理是解决与三角形中位线相关问题的重要依据。
为了更好地理解这个定理,我们可以通过以下方式来证明:如图,在△ABC 中,D、E 分别是 AB、AC 的中点,连接 DE。
延长 DE 到点 F,使得 EF = DE,连接 CF。
因为 AE = EC,∠AED =∠CEF,DE = EF,所以△ADE ≌△CFE(SAS)所以 AD = CF,∠ADE =∠F所以 AB // CF又因为 AD = BD所以 BD = CF所以四边形 BCFD 是平行四边形(一组对边平行且相等的四边形是平行四边形)所以 DF // BC,DF = BC因为 DE = 1/2 DF所以 DE // BC,DE = 1/2 BC通过以上证明,我们得出了三角形中位线定理。
三、三角形中位线定理的应用1、证明线段平行如果已知一条线段是三角形的中位线,那么可以直接得出这条线段与三角形的第三边平行。
例如,在△ABC 中,D、E 分别是 AB、AC 的中点,连接 DE,则DE // BC。
2、证明线段的数量关系可以利用中位线等于第三边的一半来证明线段之间的倍数关系。
比如,已知△ABC 中,DE 是中位线,那么 DE = 1/2 BC。
3、计算线段的长度在一些几何计算题中,如果能找到三角形的中位线,就可以利用中位线定理求出相关线段的长度。
例如,在△ABC 中,AB = 10,D、E 分别是 AB、AC 的中点,那么 DE = 5。
4、求图形的面积通过中位线与底边的关系,可以求出相关三角形的面积比。
假设△ABC 中,DE 是中位线,△ADE 的面积为 S1,△ABC 的面积为 S2。
因为 DE // BC,所以△ADE ∽△ABC,相似比为 1 : 2。
2022-2023学年初二数学第二学期培优专题14 三角形斜边中线与中位线

2022-2023学年初二数学第二学期培优专题14 三角形斜边中线与中位线结合【例题讲解】(1)如图1,已知△ABC中,F是BC上一点,AB=BF,BE⊥AF,垂足是E,D是AC的中点,请说明FC和DE有怎样的关系?(请写出详细的推理过程)(2)如图2,在△ABC中,M、D分别是边AB、AC的中点,E是线段MD上的一点.连接AE、BE,∠AEB =90°,且AB=8,BC=14,则DE的长是______.解:(1)12DE FC DE FC=∥,,理由如下:∵AB=BF,BE⊥AF,∴AE=EF,即点E是AF的中点,又∵D是AC的中点,∴DE是△ACF的中位线,∴12DE FC DE FC=∥,;(2)∵M、D分别是AB、AC的中点,∴MD是△ABC的中位线,∴172MD BC==,∵∠AEB=90°,AB=8,M是AB的中点,∴142ME AB==,∴DE=MD-ME=3.【综合演练】1.如图,在Rt△ABC中,∠ABC=90°,BF是AC边上的中线,DE是△ABC的中位线,若DE=10,则BF的长为()A .10B .5C .8D .62.如图,在ABC 中,BF 平分ABC ∠,AF BF ⊥于点F ,D 为AB 的中点,连接DF 延长交AC 于点.E 若10AB =,=16BC ,则线段EF 的长为( )A .2B .3C .4D .53.如图,在RtΔABC 中,∠ACB =90,AC =6、BC =4,点F 为射线CB 上一动点,过点C 作CM ⊥AF 于M 交AB 于E , D 是AB 的中点,则DM 长度的最小值是( )A .3B .2C .1D .6-24.如图,在正方形ABCD 中,对角线AC 与BD 相交于点O ,E 为BC 上一点,CE =5,F 为DE 的中点.若△CEF 的周长为18,则OF 的长为( )A .3B .4C .52D .72第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题(共0分)5.已知,如图,在△ABC 中,D 、E 、F 分别是各边的中点,AH 是高,已知AB =6cm ,AC =8cm ,7cm 3CH BH -=,则△DHE 的周长为________cm .6.如图,在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,D ,E ,F 分别为AB ,AC ,AD 的中点,若6BC =,则EF 的长度为 _____.7.如图,菱形ABCD 中,DE AB ⊥,垂足为E ,点F 、G 分别为边AD 、DC 的中点,5,8EF FG ==,则ABCD S =菱形___________.8.如图,在ABC 和ABD △中,90ACB ADB ∠=∠=︒,E 、F 、G 分别为AB 、AC 、BC 的中点,若1DE =,则FG =_________.9.如图,在正方形ABCD 中,F 在AB 上,E 在BC 的延长线上,AF =CE ,连接DF 、DE 、EF ,EF 交对角线BD 于点N ,M 为EF 的中点,连接MC ,下列结论:①△DEF 为等腰直角三角形;②∠FDB =∠FEC ;③直线MC 是BD 的垂直平分线;④若BF =2,则MC =2;其中正确结论的有_______.10.如图,ABC ∆中,90ACB ∠=,D 为AC 边上的中点,E 为AB 边上一点,4AB BE =,连接CE DE 、,延长DE 交CB 延长线于F ,若3BF =,10AB =,则CE =________.11.如图,在Rt ABC 中,90,8,6ACB AC BC ∠=︒==,点P 是平面内一个动点,且4AP =,Q 为BP 的中点,在P 点运动过程中,设线段CQ 的长度为m ,则m 的取值范围是_______.三、解答题(共0分)12.如图,在四边形ABCD 中,∠ABC =90°,AC=AD ,M ,N 分别是AC ,CD 的中点,连接BM ,MN ,BN .(1)求证:BM=MN;(2)若∠BAD=60°,AC平分∠BAD,AC=2.①求∠BMN的度数;②求BN的长.13.如图,D、E、F分别是△ABC三边中点,AH⊥BC于H.求证:(1)∠BDF=∠BAC;(2)DF=EH.14.在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AB,点E、F分别是OA、BC的中点,连接BE、EF.BC;(1)求证:EF=12(2)在上述条件下,若AC=BD,G是BD上一点,且BG:GD=3:1,连接EG、FG,试判断四边形EBFG的形状,并证明你的结论.15.如图,在平面直角坐标系中,A(0,4),B(4,0),C(6,2),连接AB,BC,平移BC至AD(点B 与点A对应,点C与点D对应),连接CD.(1)①直接写出点D的坐标为.②判断四边形ABCD的形状,并证明你的结论;(2)如图1,点E为AB边上一点,连接DE,DF平分∠EDC交BC于F,连接EF,若∠DFE=45°,求BE 的长;(3)如图2,N为BC边的中点,若∠AMC=90°,连接MN,请直接写出MN的取值范围.16.已知,在△ABC中,以△ABC的两边BC,AC为斜边向外测作Rt△BCD和Rt△ACE,使∠CAE=∠CBD,取△ABC边AB的中点M,连接ME,MD.特例感知:(1)如图1,若AC=BC,∠ACB=60°,∠CAE=∠CBD=45°,取AC,BC的中点F,G,连接MF,MG,EF,DG,则ME与MD的数量关系为______,∠EMD=______;(2)如图2,若∠ACB=90°,∠CAE=∠CBD=60°,取AC,BC的中点F,G,连接MF,MG,EF,DG,请猜想ME与MD的数量关系以及∠EMD的度数,并给出证明;类比探究:(3)如图3,当△ABC是任意三角形,∠CAE=∠CBD=α时,连接DE,请猜想△DEM的形状以及∠EMD 与α的数量关系,并说明理由.中,D为BC中点,BE、CF与射线AE分别相交于点E、F(射线AE不经过点D).17.在ABC(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND.求证:AM=AN(3)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND.求证:∠EMD=∠FND.18.(1)如图1,已知△ABC中,F是BC上一点,AB=BF,BE⊥AF,垂足是E,D是AC的中点,请说明FC和DE有怎样的关系?(请写出详细的推理过程)(2)如图2,在△ABC中,M、D分别是边AB、AC的中点,E是线段MD上的一点.连接AE、BE,∠AEB =90°,且AB=8,BC=14,则DE的长是______.答案与解析【例题讲解】(1)如图1,已知△ABC中,F是BC上一点,AB=BF,BE⊥AF,垂足是E,D是AC的中点,请说明FC和DE有怎样的关系?(请写出详细的推理过程)(2)如图2,在△ABC中,M、D分别是边AB、AC的中点,E是线段MD上的一点.连接AE、BE,∠AEB =90°,且AB=8,BC=14,则DE的长是______.解:(1)12DE FC DE FC=∥,,理由如下:∵AB=BF,BE⊥AF,∴AE=EF,即点E是AF的中点,又∵D是AC的中点,∴DE是△ACF的中位线,∴12DE FC DE FC=∥,;(2)∵M、D分别是AB、AC的中点,∴MD是△ABC的中位线,∴172MD BC==,∵∠AEB=90°,AB=8,M是AB的中点,∴142ME AB==,∴DE=MD-ME=3.【综合演练】1.如图,在Rt△ABC中,∠ABC=90°,BF是AC边上的中线,DE是△ABC的中位线,若DE=10,则BF的长为()A.10 B.5 C.8 D.6【分析】根据三角形中位线定理求出AC ,根据直角三角形的斜边上的中线等于斜边的一半计算,得到答案.【解答】解:∵DE 是△ABC 的中位线,若DE =10,∴AC =2DE =20,在Rt △ABC 中,∠ABC =90°,BF 是AC 边上的中线,∴BF =12AC =10,故选:A . 【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.2.如图,在ABC 中,BF 平分ABC ∠,AF BF ⊥于点F ,D 为AB 的中点,连接DF 延长交AC 于点.E 若10AB =,=16BC ,则线段EF 的长为( )A .2B .3C .4D .5 【答案】B【分析】先求出152DF AB AD BD ====,然后证明DE BC ∥,根据平行线分线段成比例可得=AE EC ,再根据三角形中位线定理求出DE 即可.【解答】解:AF BF ⊥,90AFB ∴∠=︒,10AB =,D 为AB 中点,152DF AB AD BD ∴====, ABF BFD ∠∠∴=,又BF 平分ABC ∠,ABF CBF ∠∠∴=,CBF DFB ∠∠∴=,∴DE BC ∥,∴=AD AE DB EC,182DE BC ∴==, 853EF DE DF ∴=-=-=,故选:B .【点评】本题考查了直角三角形斜边中线的性质,等腰三角形的判定和性质,平行线的判定,平行线分线段成比例定理以及三角形中位线定理等知识,证明DE BC ∥是解答本题的关键.3.如图,在RtΔABC 中,∠ACB =90,AC =6、BC =4,点F 为射线CB 上一动点,过点C 作CM ⊥AF 于M 交AB 于E , D 是AB 的中点,则DM 长度的最小值是( )A .3B .2C .1D .6-2【答案】C【分析】取AC 的中点T ,连接DT ,MT .利用三角形的中位线定理求出DT ,利用直角三角形的中线的性质求出MT ,再根据DM MT DT ≥-,可得结论.【解答】解:如图,取AC 的中点T ,连接DT ,MT .∵AD DB =,AT TC =,∴122DT BC ==. ∵CE AF ⊥,∴90AMC ∠=︒,∴132TM AC ==, ∴点M 的运动轨迹是以T 为圆心,TM 为半径的圆,∴321DM TM DT ≥-=-=,∴DM 的最小值为1,故选:C .【点评】本题考查点与圆的位置关系,三角形中位线定理,直角三角形斜边中线的性质等知识,解题的关键是学会添加常用辅助线,构造三角形中位线,直角三角形斜边中线解决问题.4.如图,在正方形ABCD 中,对角线AC 与BD 相交于点O ,E 为BC 上一点,CE =5,F 为DE 的中点.若△CEF 的周长为18,则OF 的长为( )A .3B .4C .52D .72 【答案】D【分析】先根据直角三角形的性质求出DE 的长,再由勾股定理得出CD 的长,进而可得出BE 的长,由三角形中位线定理即可得出结论.【解答】∵CE=5,△CEF 的周长为18,∴CF+EF=18-5=13.∵F 为DE 的中点,∴DF=EF .∵∠BCD=90°,∴CF=12DE ,∴EF=CF=12DE=6.5,∴DE=2EF=13,∴CD=2212DE CE -=,∵四边形ABCD是正方形,∴BC=CD=12,O为BD的中点,∴OF是△BDE的中位线,∴OF=12(BC-CE)=12(12-5)=3.5,故选D.【点评】本题考查的是正方形的性质,涉及到直角三角形的性质、三角形中位线定理等知识,难度适中.使用勾股定理是解决这个问题的关键.5.已知,如图,在△ABC中,D、E、F分别是各边的中点,AH是高,已知AB=6cm,AC=8cm,7 cm 3CH BH-=,则△DHE的周长为________cm.【答案】496##186【分析】根据直角三角形斜边上的中线的性质求出DH,根据三角形中位线定理求出DE,根据三角形的周长公式计算,得到答案.【解答】解:∵AH是△ABC的高,∴∠AHB=90°,∵点D是AB的中点,∴DH=12AB=12×6=3cm,∵D、E分别是BA、BC的中点,∴DE是△ABC的中位线,∴DE=12AC=12×8=4cm,∵BE=EC,CH-BH=73 cm,∴HE=76 cm,∴△DHE的周长=DH+DE+HE=496cm,故答案为:496.【点评】本题考查的是三角形中位线定理、直角三角形斜边上的中线的性质,掌握三角形中位线等于第三边的一半是解题的关键.6.如图,在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,D ,E ,F 分别为AB ,AC ,AD 的中点,若6BC =,则EF 的长度为 _____.【答案】3【分析】根据含30°的直角三角形的性质求出CD ,根据直角三角形的性质求出CD ,根据三角形中位线定理计算,得到答案.【解答】解:∵∠ACB =90°,∠A =30°,∴AB =2BC =12.∵∠ACB =90°,D 为AB 的中点,∴CD =12AB =6,∵E ,F 分别为AC ,AD 的中点,∴EF 为△ACD 的中位线,∴EF =12CD =3.故答案为:3.【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.7.如图,菱形ABCD 中,DE AB ⊥,垂足为E ,点F 、G 分别为边AD 、DC 的中点,5,8EF FG ==,则ABCD S =菱形___________.【答案】96【分析】连接,AC BD ,交于点O ,先根据直角三角形斜边上的中线等于斜边的一半可得10AD =,再根据三角形的中位线定理可得16AC =,然后根据菱形的性质和勾股定理可得12BD =,最后利用菱形的面积公式即可得.【解答】解:如图,连接,AC BD ,交于点O ,,5DE AB EF ⊥=,且点F 为边AD 的中点,210AD EF ∴==,点,F G 分别为边,AD DC 的中点,8FG =,216AC FG ∴==,四边形ABCD 是菱形,1,8,22AC BD OA AC BD OD ∴⊥===, 226OD AD OA ∴=-=,12BD ∴=,1116129622ABCD S AC BD ∴=⋅=⨯⨯=菱形, 故答案为:96.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半、三角形的中位线定理、勾股定理、菱形的性质,熟练掌握菱形的性质是解题关键.8.如图,在ABC 和ABD △中,90ACB ADB ∠=∠=︒,E 、F 、G 分别为AB 、AC 、BC 的中点,若1DE =,则FG =_________. 【答案】1【分析】由直角三角形斜边中线的性质得出AB =2DE ,再由三角形中位线的性质可得FG 的长;【解答】解:∵Rt △ABC 中,点E 是AB 的中点,DE =1,∴AB =2DE =2,∵点F 、G 分别是AC 、BC 中点,∴112FG AB ==,故答案为:1【点评】本题考查了直角三角形的性质及三角形中位线的性质等知识;熟练掌握中位线定理是解题的关键. 9.如图,在正方形ABCD 中,F 在AB 上,E 在BC 的延长线上,AF =CE ,连接DF 、DE 、EF ,EF 交对角线BD 于点N ,M 为EF 的中点,连接MC ,下列结论:①△DEF 为等腰直角三角形;②∠FDB =∠FEC ;③直线MC 是BD 的垂直平分线;④若BF =2,则MC =2;其中正确结论的有_______.【答案】①②③④【分析】先根据SAS 定理证出ADF CDE ≅,再根据全等三角形的性质可得,DF DE ADF CDE =∠=∠,然后根据等腰直角三角形的判定即可判断①;先根据等腰直角三角形的性质可得45DEF DFE ∠=∠=︒,再根据对顶角相等可得DNF BNE ∠=∠,然后根据三角形的内角和定理即可得判断②;连接BM DM ,,先根据直角三角形斜边上的中线等于斜边的一半可得12BM DM EF ==,再根据线段垂直平分线的判定即可判断③;取BE 的中点O ,连接MO ,先根据三角形中位线定理可得11,2MO BF MO BF ==∥,再根据等腰三角形的三线合一可得1452BCM BCD ∠=∠=︒,然后在Rt MOC 中,利用勾股定理即可得.【解答】解:四边形ABCD 是正方形,,90,45AB AD CD BC A ABC BCD ADC CBD ∴===∠=∠=∠=∠=︒∠=︒,在ADF △和CDE 中,90AD CD A DCE AF CE =⎧⎪∠=∠=︒⎨⎪=⎩,()SAS ADF CDE ∴≅,,DF DE ADF CDE ∴=∠=∠,90EDF CDE CDF ADF CDF ADC ∴∠=∠+∠=∠+∠=∠=︒,DEF ∴为等腰直角三角形,结论①正确;45DEF DFE ∴∠=∠=︒,又45,CBD DNF BNE ∠=︒∠=∠,180180DNF CBD BN E E DF ∴︒-∠=︒-∠-∠∠-,即FDB FEC ∠=∠,结论②正确;如图,连接BM DM ,,M 为Rt DEF △和Rt BEF △斜边EF 上的中点,12BM DM EF ∴==, 又BC CD =,∴直线MC 是BD 的垂直平分线,结论③正确;如图,取BE 的中点O ,连接MO ,1121,22MO BF MO BF ∴==⨯=∥,90MOC ABC ∴∠=∠=︒,直线MC 是BD 的垂直平分线,BC CD =,1452BCM BCD ∴∠=∠=︒(等腰三角形的三线合一), Rt COM ∴是等腰直角三角形,且1OC MO ==,222MC MO OC ∴=+=,结论④正确;综上,正确结论的有①②③④,故答案为:①②③④.【点评】本题考查了正方形的性质、三角形全等的判定与性质、等腰直角三角形的判定与性质、勾股定理、线段垂直平分线的判定、三角形中位线定理等知识点,熟练掌握各判定与性质是解题关键.10.如图,ABC ∆中,90ACB ∠=,D 为AC 边上的中点,E 为AB 边上一点,4AB BE =,连接CE DE 、,延长DE 交CB 延长线于F ,若3BF =,10AB =,则CE =________.【答案】972【分析】取AB 的中点G ,连接DG ,则AB =2BG ,可得BE =EG ,再利用三角形中位线定理得BC =2DG ,DG BF ∥,利用ASA 证明△GDE ≌△BFE ,得DG =BF =3,DE =EF ,从而解决问题.【解答】解:取AB 的中点G ,连接DG ,则AB =2BG ,∵AB =4BE ,∴BE =EG ,∵D 为AC 边上的中点,G 为AB 的中点,∴DG 为△ABC 的中位线,∴BC =2DG ,DG BF ∥, ∴∠GDE =∠F ,在△GDE 和△BFE 中,GDE F DEG FEB GE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△GDE ≌△BFE (ASA ),∴DG =BF =3,DE =EF ,∴BC =6,∴CF =9,由勾股定理得,AC =8,∴CD =4,在Rt △CDF 中,由勾股定理得,DF =22224997CD CF +=+=,∵∠ACB =90°,EF =DE ,∴CE =12DF =972, 故答案为:972. 【点评】本题主要考查了勾股定理,三角形中位线定理,全等三角形的判定与性质,直角三角形斜边上中线的性质等知识,证明点E 是DF 的中点是解题的关键.11.如图,在Rt ABC 中,90,8,6ACB AC BC ∠=︒==,点P 是平面内一个动点,且4AP =,Q 为BP 的中点,在P 点运动过程中,设线段CQ 的长度为m ,则m 的取值范围是_______.【答案】3m 7≤≤【分析】取AB 的中点M ,连接QM 、CM ,得到QM 是△APB 的中位线,CM 是Rt ABC 斜边上的中线,求得QM 、CM 的长,在△QMC 中利用三角形三边关系得到CQ 的范围即可.【解答】取AB 的中点M ,连接QM 、CM ,∴QM 是△APB 的中位线,CM 是Rt ABC 斜边上的中线,∴122QM AP ==,12CM AB =, 在Rt ABC 中,90,8,6ACB AC BC ∠=︒==,∴226810AB =+=,∴CM =5,∵点P 是平面内一个动点,∴点Q 是动点,且点Q 以点M 为圆心,QM 长为半径的圆上运动,∴C 、Q 、M 可以三点共线,∴CM -MQ ≤CQ ≤CM +MQ ,∴3m 7≤≤,故答案为:3m 7≤≤.【点评】本题考查勾股定理、直角三角形斜边中线的性质,中位线定理、三角形三边关系等知识,分析点Q 的运动是解题的关键.12.如图,在四边形ABCD 中,∠ABC =90°,AC=AD ,M ,N 分别是AC ,CD 的中点,连接BM ,MN ,BN .(1)求证:BM=MN ;(2)若∠BAD =60°,AC 平分∠BAD ,AC =2.①求∠BMN 的度数;②求BN 的长.题的关键是灵活应用三角形的中位线平行于第三边,并且等于第三边的一半.13.如图,D、E、F分别是△ABC三边中点,AH⊥BC于H.求证:(1)∠BDF=∠BAC;(2)DF=EH.【答案】(1)见解析;(2)见解析.【分析】(1)根据三角形中位线定理得到DF//AC,根据平行线的性质证明结论;AC,等量代换证明结论.(2)根据直角三角形的性质得到EH=12【解答】(1)∵D、F分别是△ABC两边中点,∴DF是△ABC的中位线,AC,∴DF//AC,DF=12∴∠BDF=∠BAC;(2)∵AH⊥BC于H,E是AC的中点,AC,∴EH=12由(1)得,DF=12 AC,∴DF=EH.【点评】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.14.在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AB,点E、F分别是OA、BC的中点,连接BE、EF.BC;(1)求证:EF=12(2)在上述条件下,若AC=BD,G是BD上一点,且BG:GD=3:1,连接EG、FG,试判断四边形EBFG的形状,并证明你的结论.∴EBFG是平行四边形,连接CG,∵G是OD的中点,而CO=12AC=12BD=AB=CD,∴CG⊥OD,而F是BC的中点,∴GF=12BC=BF,∴平行四边形EBFG是菱形.【点评】本题考查了平行四边形的性质和判定,矩形性质,菱形性质,三角形的中位线,直角三角形斜边上中线性质,等腰三角形的性质等知识点,主要考查学生综合运用定理进行推理的能力,注意:直角三角形斜边上中线等于斜边的一半.15.如图,在平面直角坐标系中,A(0,4),B(4,0),C(6,2),连接AB,BC,平移BC至AD(点B 与点A对应,点C与点D对应),连接CD.(1)①直接写出点D的坐标为.②判断四边形ABCD的形状,并证明你的结论;(2)如图1,点E为AB边上一点,连接DE,DF平分∠EDC交BC于F,连接EF,若∠DFE=45°,求BE 的长;(3)如图2,N为BC边的中点,若∠AMC=90°,连接MN,请直接写出MN的取值范围.段CD上取一点G,使DG=DE,∵∠FDE=∠FDG,DF=DF,∴△DFE≌△DFG(SAS),∴∠DFE=∠DFG=45°,EF=GF,∴∠EFG=90°,∵∠EFB+∠GFC=90°,∠GFC+∠FGC=90°,∴∠EFB=∠FGC,∵∠EBF=∠FCG=90°,EF=GF,∴△EBF≌△FCG(AAS),∴EB=FC,BF=CG,设EB=FC=x,则22BF CG BC x x==-=-,∴222222(42)(22)DE AE AD x DG=+=-+=,∵222()(4222)DG CD GC x=-=-+,∴222 (4222)(42)(22)x x-+=-+,解得:423x,即423BE=;(3)解:如图,连接AC,取AC的中点H,连接MH,NH,∵点A(0,4),B(4,0),D(2,6),∴42,210AB AC==,∵H为AC的中点,N为BC边的中点,∴1122,1022NH AB HM AC====,∵HM-NH≤MN≤HM+NH,∴MN的取值范围为10222210MN-≤≤+.【点评】本题是四边形综合题,主要考查了平行四边形和矩形的性质、三角形全等、勾股定理的运用,直角三角形的性质,三角形中位线定理等,综合性强,难度较大,熟练掌握相关知识点是解题的关键.16.已知,在△ABC中,以△ABC的两边BC,AC为斜边向外测作Rt△BCD和Rt△ACE,使∠CAE=∠CBD,取△ABC 边AB 的中点M ,连接ME ,MD .特例感知:(1)如图1,若AC =BC ,∠ACB =60°,∠CAE =∠CBD =45°,取AC ,BC 的中点F ,G ,连接MF ,MG ,EF ,DG ,则ME 与MD 的数量关系为______,∠EMD =______;(2)如图2,若∠ACB =90°,∠CAE =∠CBD =60°,取AC ,BC 的中点F ,G ,连接MF ,MG ,EF ,DG ,请猜想ME 与MD 的数量关系以及∠EMD 的度数,并给出证明;类比探究:(3)如图3,当△ABC 是任意三角形,∠CAE =∠CBD =α时,连接DE ,请猜想△DEM 的形状以及∠EMD 与α的数量关系,并说明理由. 【答案】(1)ME=MD ,∠EMD=90°;(2)ME=MD ,∠EMD=120°;(3)△DEM 是等腰三角形,∠EMD=2α.【分析】(1)如图1,证明△EAM ≌△DBM ,可得EM=DM ,先根据三角形的中位线得:11FM AC MG BC 22===,由直角三角形斜边中线等于斜边一半可得12EF AC =,得EF=FM ,且顶角∠EFM=150°,得∠FEM=∠FME=15°,同理∠DMG=15°,相加可得结论;(2)如图2,证明△MEF ≌△DMG ,可得EM=DM ,∠EMF=∠MDG=15°,相加可得∠EMD=120°;(3)如图,作辅助线,取AC ,BC 的中点F ,G ,连接MF ,MG ,EF ,DG ,同理可证出EF=MG ,DG=FM ,∠3=2∠2,∠4=2∠1,证明△MEF ≌△DMG .则EM=DM ,∠EMF=∠MDG .表示∠EMD=∠MDG+∠DMG+∠ACB ,代入可得结论.【解答】解:(1)ME=MD ,∠EMD=90°;理由是:如图1,∵AC=BC ,∠ACB=60°,∴△ABC 是等边三角形,∴∠CAB=∠CBA=60°,在 Rt △BCD 和Rt △ACE 中,∠CAE=∠CBD=45°,∴AC=2AE,BC=2BD,∴AE=BD,∵M是AB的中点,∴AM=BM,∵∠EAM=45°+60°=105°,∠DBM=45°+60°=105°,∴∠EAM=∠DBM,∴△EAM≌△DBM,∴EM=DM,∵F、G分别是AC、BC的中点,∴FM=MG=12AC=CF=CG,∴四边形CFMG是菱形,∴∠FMG=∠BCA=60°,Rt△ACE中,∵F是斜边AC的中点,∴EF=12AC=FM,∵∠EFM=90°+60°=150°,∴∠FEM=∠FME=15°,同理∠DMG=15°,∴∠EMD=60°+15°+15°=90°,故答案为EM=DM,90°;(2)ME=MD,∠EMD=120°;证明:∵F,G,M是△ABC的三边AC,BC,AB的中点,∴FM=12BC=CG,FM∥BC,MG=12AC=CF,MG∥AC.∴四边形CFMG是平行四边形,∴∠AFM=∠FMG=∠ACB=∠MGD=90°.∵∠AEC=∠BDC=90°,F,G是AC,BC的中点,∴EF=AF=FC=12AC,CG=BG=DG=12BC.∴∠2=∠CEF,∠1=∠CDG,EF=MG,DG=FM.∴∠3=∠2+∠CEF=2∠2,∠4=∠1+∠CDG=2∠1.∵∠2+∠EAC=90°,∠1+∠CBD=90°,∠CAE=∠CBD=60°,∴∠1=∠2=30°.∴∠3=∠4=60°.∴∠EFM=∠3+∠AFM=150°,∠DGM=∠4+∠CGM=150°∴∠EFM=∠DGM.又∵EF=MG,FM=DG,∴△MEF≌△DMG.∴EM=DM,∠EMF=∠MDG=15°.∴∠EMD=90°+2×15°=90°30°=120°;(3)△DEM是等腰三角形,∠EMD=2α.证明:取AC,BC的中点F,G,连接MF,MG,EF,DG,同(2)证法相同,可证出EF=MG,DG=FM,∠3=2∠2,∠4=2∠1.∵∠2+∠EAC=90°,∠1+∠CBD=90°,∠CAE=∠CBD=α,∴∠1=∠2=90°-α.∴∠3=∠4=2(90°-α).∴∠EFM=∠3+∠AFM=∠3+∠ACB,∠DGM=∠4+∠BGM=∠4+∠ACB.∴∠EFM=∠DGM.又∵EF=MG,FM=DG,∴△MEF≌△DMG.∴EM=DM,∠EMF=∠MDG.∴△DEM是等腰三角形;∵∠EMD=∠FME+∠FMG+∠DMG,由(2)知∠FMG=∠ACB,∴∠EMD=∠MDG+∠DMG+∠ACB.∵∠MDG+∠DMG=180°-∠DGM=180°-(∠4+∠ACB )=180°-2(90°-α)-∠ACB=2α-∠ACB.∴∠EMD=2α-∠ACB+∠ACB=2α.【点评】本题是三角形的综合题,考查了三角形全等的性质和判定、三角形中位线定理、直角三角形斜边中线的性质、平行四边形的性质、等边三角形的性质等知识,并运用了类比的思想依次解决问题.∆中,D为BC中点,BE、CF与射线AE分别相交于点E、F(射线AE不经过点D).17.在ABC(1)如图①,当BE∥CF时,连接ED并延长交CF于点H. 求证:四边形BECH是平行四形;(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND.求证:AM=AN(3)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND.求证:∠EMD=∠FND.【答案】(1)证明见解析(2)证明见解析(3)证明见解析【分析】(1)根据两直线平行内错角相等求得∠DBE=∠DCH,然后依据ASA求得BDE≅CDH得出ED=HD,最后根据有一组对边平行且相等的四边形是平行四边形求得.(2)连接FD、ED,延长ED交CF于点H,根据直角三角形斜边的中线定理和三角形的中位线定理求得ME=DN,MD=NF,从而证得AM=AN;(3)在(2)的条件下根据SSS 即可证明MED ≅NDF ,最后根据全等三角形的对应角相等求得∠EMD =∠FND . (1)如图①,∵D 为BC 的中点,∴BD =CD ,∵BE ∥CF ,∴∠DBE =∠DCH ,在BDE 与CDH 中,DBE DCH BD CD BDE CDH ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴BDE ≅CDH (AAS ),∴ED =HD ,∴四边形BECH 是平行四边形;(2)如图②连接FD 、ED ,延长ED 交CF 于点H ,∵BE ⊥AE ,CF ⊥AE ,)可知BDE≅CDHRt EHFRt AEBRt ACF在MED与NDF∴MED≅NDF。
中位线的构造

八下数学思维解法技巧培优小专题【典例丄】(2019-赤壁市模拟)如图,在四边形肋CD 中,点分别是边AB 、AD 的中点,若BC=15, CD=9, EF=6, ZAFE=55° ,则ZQC= 145 °・【点拨】连接BD •根据三角形中位线定理得到肋=2£F=12, £F 〃肋,根据勾股定理的逆定理得到ZBDC=9Q° ,结合图形计算即可.【解析】解:连接BD ,T 点F 分别是边AB. AD 的中点,:.BD=2EF=12, EF//BD.:• ZADB= ZAFE=55° ,BD 2+CD 2=225, 卅=225,:.BD 2+CD 2=BC 19:.ZBDC=90° ,••• ZADC= ZADB+ZBDC= 145° ,故答案为:145. 连接两点构造中位线中佞线的构31A・100°B. 120° C. 140°D・160°【典例2】(2019・宁波期末)如图,在0BC中D E分别是.IB, AC的中点,点F, G在BC上,且BC=4BF=4CG, £F 与DG 相交于点O,若ZDFE=40° , ZZ)GE=80°,那么ZDOE的度数是()A【点拨】连接皿利用中位线的性质,可得DE=;BC,由BC=4BF=4CG可得FG= *BC,易得DE //FGRDE=FG,易得四边形DEFG为平行四边形,可得DF//EG,利用平行线的性质可得ZDGE= Z FDG,由外角的性质可得结果.【解析】解:连接DE,TD, E分别是.IB, AC的中点,:.DE//BC且9:BC=4BF=4CG,:.FG=^BC,.•・四边形DEFG为平行四边形,:.DF//EG.:• ZDGE= ZFDG=W ,V ZP/T=40°,I CDCZD利用"••• ZDOE=80° +40° =120° ,【典例3】(2019・钦州期末)如图,MBC中,M是EC中点…Q平分ZBAC. ED丄“10于D,若AB=12, JC=16,则MD等于2・【点拨】延长他交zlC于H 根据等腰三角形的性质得到BD=DH.根据三角形中位线定理计算即可.【解析】解:延长交JC于H,T.1D 平分ABAC. BDW:・BD=DH、AH=4B=\2,:.HC=AC-AH=4.TM 是EC 中点,BD=DH,:.MD=字CH=2,故答案为:2.AB【典例4】(2019・南开区期中)如图,HABC中一3是中线,AE是角平分线,CF丄于F」B=5,AC=2.则DF的长为()A. 3B. 2.5 C・ 1.5 D・1【点拨】延长CF交肋于证明MFCs/XAFH可得CF=FH, AH=4C,然后求岀EH,再根据三角形的中位线平行于第三边并且等于第三边的一半可得詁丹.【解析】解:如图,延长CF交肋于H,•••一匹是角平分线,A ZCAF= ZHAF.TCF 丄A ZJFC=Z.4FH=90° ,在△JFC和厶1?7/中.Z.CAF =乙HAFT AF =AF ,LAFC=乙AFH•••△zLFCPZUFH (如),:・CF=FH・ AH=AC,:.BH=AB - .1H=AB - AC=5・2 = 3,又•••.ID是中线,•••DF是的中位线, :.DF=^BH=^x3 = 1.5. 故选:C.区中点构造中位线【典例5】(2019-成都期末)已知:如图一Q、恥分别是厶拐C的中线和角平分线—3丄BE, AD=BE3^5-2 —【点拨】过D点作DF//BE,则DF=^BE=\. F为EC中点.在RtZ^WF中求岀的长度,根据已知条件易知G为3中点,因此E为廿中点,贝ij AC= |jF.【解析】解:过刀点作DF//BE.•••・!□是AABC的中线,AD丄BE,:・F为EC中点,AD丄DF,【典例6](2019-福田如图,已知在3=24,点E是BC上一点,BE=10,连接DE、\\1D=BE=2,则DF=X V22 + 12 =屈「BE是AABC的角平分线,.10丄PE•••△dEG 幻△DEG,•••G为中点,•••E为M中点,:・AE=EF=CF,故答案为:芋【点拨】连接取加的中点F,连接MF、NF,证明NF、分别是△PDE、肋的中位线,由三角形中位线定理得出NF〃恥,MF//AD、NF= ^BE=5. MF=^AD= 12.证出AF丄MF,在Rt/\MNF中,由勾股龙理即可得出答案・CB【解析】解:连接取肋的中点F,连接MF、NF、如图所示:TM、N、F分别是DE、BD的中点,:・NF、妙分别是△$£)£、厶血的中位线,:.NF//BE. MF//AD, NF=;BE=5,临=訓=\2.V ZJCB=90° ,•••JD 丄BC、\9MF//AD.•••MF 丄BC.•:NFUBE、•••NF 丄MF.在Rt^MNF中,由勾股宦理得:MN= \NF2 + MF2=^52 + 122 =13;故答案为:13.【典例刀(2019-成都校级月考)如图,41BC中,ZJ5C=90° , BA=BC.△BEF为等腰直角三角形, ZBEF=9L , M为2F的中点,求证:ME=^CF・E【点拨】延长EF到D, DE=EF,连接JD、BD,判断岀是等腰直角三角形,根据等峻血角三角形的性质可得加=BF,再求出ZCBF= ZABD,然后利用“边角边”证明&BD和ZkCBF全等,根据全等三角形对应边相等可得.3=CF,再根据三角形的中位线平行于第三边并且等于第三边的一半可得ME=i W,从而得到ME= i-CF・【解析】证明:如图,延长EF到D,l-li DE=EF,连接肋、BD,••仏BEF为等腰直角三角形,ZBEF=9L ,•••ZBFE=45° , BE丄DF,•••恥垂直平分DF,A ZBDE=45° ,:・、BDF是等腰直角三角形,:・BD=BF. ZDBF=90° ,V ZCBF+Z.1BF= Z ABC= 90° ,ZABLH ZABF= ZDBF= 90c,:.ZCBF=Z.1BD.在HABD和ZkCBF 中,AB = BC乙CBF = J LABD^BD = BF:.AABD^ACBF (SAS).:・AD=CF.•・・M为.IF的中点,DE=EF,:.ME是ZUDF的中位线,:.ME=【典例8】(2019-成都校级月考)如图,点P为'ABC的边EC的中点,分别以AC为斜边作RtZD 和RtAJC£> 且ZB3=Za(E,求证:PD=PE.【点拨】如图,分别取肿、JC的中点M M连接DM、PM、PN、NE,构建三角形中位线,利用三角形中位线左理和直角三角形斜边的中线等于斜边的一半证得3DP沁NPE (SJS),则该全等三角形的对应边相等:PD=PE・【解析】证明:如图,分别取肿、2C的中点M、N,连接DM、PM、PN、NE.•・•点P为HABC的边BC的中点,.・.PM为/\ABC的中位线,:.PM=扣C・又TWE为直角斜边上的中线,:・NE=AN=扣C.:・MP=NE・同理DM=RV・TD忆=桃AZ1 = Z3,・・・Z5=2Z1 (三角形外角定理).同理,Z6=2Z2.又Z1 = Z2,AZ5=Z6.又PM//AC, PN//AB,AZ7=Z9, Z8=Z9,AZ7=Z &•••Z5+Z7=Z6〒Z8,即ZDMP= ZPNE,DM = PM:.在\MDP与ANPE中,乙DMP =厶PNE,MP = NE:.HMDPS HNPE(SAS),:・PD=PE・1.(2019・武汉)如图,在△.ISC中,ZJCB=60°C=l, D是边,毎的中点,E是边BC上一点.若^平分△磁的周长,则DE的长是_亨_.【点拨】延长BC至使CM=CA,连接MM,作CN丄于M 根据题意得到ME=£P,很据三角形中位线宦理得到根据等腰三角形的性质求岀厶1CN,根据正弦的概念求岀汁算即可.【解析】解:延长BC至M,使CM=CA.连接凡皿作CN丄凡“于N,•••DE平分ZU5C的周长,:.ME=EB.又AD=DB,B. 20C. 12 D ・10:.DE= jjM, DE//AM.V ZJCB=60° ,A ZJCM= 120° ,VCM=G4,A ZJCV=60°、AN=MN 、:..4N=AC^mZACN=学\/3t• nr — J3• • DE — •故答案为:■-—・22・(2019・宽城区期末)如图,D 是ZUBC 内一点,BD 丄CD, E 、F 、G 、H 分别是边AB 、BD 、CD. AC 的中点.若-W=10, BD=J CD=6,则四边形EFGH 的周长是( )【点拨】利用勾股定理列式求出BC 的长,再根据三角形的中位线平行于第滋并且等于第三边的一半A. 24求出EH=FG= ^BC. EF=GH=*1D,然后代入数据进行讣算即可得解.【解析】解:•:BD1CD,肋=8, 3=6,:・BC= \BD2 +CD2 = V 82+ 62=10,•:E、F、G、H分别是AB. AC. CD、的中点,:・EH=FG=专BC, EF=GH=4D,•••四边形EFGH的周长=EH+GH+FG+EF=AD-BC,又mo,•••四边形EFGH的周长=10+10=20,故选:B.3・(2019・英徳市期末)如图,在中,BF平分ZABC, AG丄BF,垂足为点交BC于点G, E为/C的中点,连结DE, DE=2.5cm, AB=4cm,则BC的长为9 期・【点拨】由条件“BF平分AG丄肿•'可判怎三角形肋G是等腰三角形(AB=GB).再由条件临为HC的中点”,可判怎a是三角形的中位线,由此可得GC=2DE 进而可求出BC的长.【解析】解:TEF 平分ZABC. AG丄BF.:./\ABG是等腰三角形,A. 3 D ・4AB ~ GB =4d ♦•:BF 平分 ZABC.:..4D=DG.YE 为dC 的中点,.・.D£是ZUGE 的中位线,:.DE= *CG,:.CG=2DE=5cm.:.BC=BG+CG=4+5 = 9m ,故答案为:94. (2019-通川区期末)如图,/\ABC 中,D 、E 分别是BC 、AC 的中点,平分ZABC,交DE 于点、F, 若BC=6、则DF 的长是( )【点拨】利用中位线怎理,得到DE 〃肋,根据T •行线的性质,可得ZEDC=ZABC 、再利用角平分线 的性质和三角形内角外角的关系,得到进而求出DF 的长.【解析】解:在△肋C 中,D 、E 分别是BC 、AC 的中点,:.DE//AB,:.ZEDC= ZABC. 2•:BF平分ZABC.:.ZEDC=2ZFBD・在△BDF 中,ZEDC= ZFBD+ZBFD.:.ZDBF=ZDFB・:.FD=BD= ;BC= | x6 = 3・故选:2.5.(2019-松北区一模)如图,和BE分别为三角形MC的中线和角平分线,.Q丄BE,若AD=BE=4,则FC的长」【点拨】过D点作〃恥,则F为EC中点,在RtAADF中求出2F的长度,根据已知条件易知6为3中点,因此E为廿中点,则AC=【解析】解:过D点作DF〃EE,如图所示:•••JD是ZUBC的中线,AD丄BE,;・F为EC中点,AD丄DF,\\1D=BE=4.则DF=2, AF= \!AD2 + DF2 =2>/5,•:BE是HABC的角平分线…ID丄:.HABG 竺4DBG,:.AC= |jF=3 洛.故答案为:3尽6.(2019-垦利区期末)如图,在四边形ABDC中,E、F、G、H分别为」B、BC、CD、的中点,并且E、F、G、H四点不共线.当AC=6, BD=*时,四边形EFGF的周长是一14 .【点拨】根据三角形中位线宦理得到FG〃EH, FG=£H根据平行四边形的判左龙理和周长解答即可.【解析】解:TF,G分别为BC, CD的中点,:.FG= FG//BD.VE, H分别为AB, D」的中点,•••EH=$BD=4, EH//BD.:.FG//EH. FG=EH,•••四边形EFGH为平行四边形,:.EF=GH=^1C=3.•••四边形EFGH的周长=3+3+4+4 =14,故答案为:147.(2019・怀化)已知:如图,在HABC中,DE、DF是/XABC的中位线,连接EF. AD,其交点为O・求证:(1)HCDE9HDBF;(2)O4 = OD・【点拨】(1〉根据三角形中位线,可得DF打CE的关系,DB 口 DC的关系,根据SAS.可得答案;(2)根据三角形的中位线,可得DF与AE的关系,根据平行四边形的判定与性质,可得答案.【解析】证明:(1)•:DE、DF是ZL3C的中位线,:.DF=CE. DF//CE. DB=DC・•: DF"CE、:•乙C=ZBDF ・DC = BD住HCDE和△DBF中厶C=乙BDF.CE = DF:.△ CDE9 /XDBF(SJS):(2) •:DE、DF是WBC的中位线,:.DF=AE, DF//AE,•••四边形DE.1F是平行四边形,•:EF 口.10 交于O 点,:.AO=OD8・(2019-尚志市期中)如图在直角HABC中,ZBAC=9Q Q,点D是BC中点,连接,3,点E为.Q的中点,过点/作AF//BC 交线段恥的延长线于点F,连接CF.(1)求iiE: -1F=DC;(2)在不添加任何辅助线的情况下,请直接写出所有而积等于ZUEF而枳2倍的三角形.【点拨】(1)由“MS”町证HAFE皿DBE;(2)根据等髙模型即可解决问题.【解析】证明:(1)•:AF〃BC、:.ZAFE= ZDBE•••△4BC是宜角三角形,.3是BC边上的中线,E是的中点,:..1E=DE. BD=CD在和△DBE中,LAFE =乙DBELAEF =乙BED,AE = DE:.^AFE^ADBE (zUS):(2)解:•:AE=DE・•: S ABD=2S「.BDE=2S• AEF・•:DB=DC、BD=AF, :..1F=CD9/.四边形ADCF是平行四边形,S; ADC=s; dCF=s(ABF;•••而积等于而枳2倍的三角形有:0CD, £\ABD、ZUCF. “AFB.。
初中数学知识归纳三角形的中线与中位线

初中数学知识归纳三角形的中线与中位线初中数学知识归纳:三角形的中线与中位线在初中数学中,我们学习了许多三角形的性质和相关定理。
其中,三角形的中线与中位线是三角形研究中非常重要的概念。
它们不仅可以帮助我们理解三角形的特性,还可以应用于解决实际问题。
本文将对三角形的中线与中位线进行归纳,帮助我们更好地理解和应用这些知识。
一、三角形的中线1. 定义:三角形的中线是连接三角形任意两个顶点与对边中点的线段。
2. 性质:a. 三角形的三条中线交于一点,称为重心。
三角形的重心离三角形的各顶点的距离满足重心判定定理,即离重心的距离比离顶点的距离小两倍。
b. 重心将各中线分成两比一的部分,即重心到中点的距离是中心到对边两个端点的距离的两倍。
3. 应用:中线的性质在许多三角形问题中都有重要应用,如:a. 判断三角形形状:如果三角形的中线相等,则该三角形是等边三角形。
b. 计算面积:可以利用中线分割三角形,将大三角形的面积拆分成三个小三角形的面积之和,进而进行计算。
二、三角形的中位线1. 定义:三角形的中位线是连接三角形任意两个中点的线段。
2. 性质:a. 三角形的三条中位线交于一点,称为重心。
与中线的性质相同,重心将各中位线按照两比一的比例分成两部分。
b. 三角形的中位线和中线互称,即可称中线为中位线,也可称中位线为中线。
3. 应用:中位线的性质同样在解决三角形问题中具有重要作用:a. 判断三角形形状:如果三角形的中位线相等,则该三角形是等边三角形。
b. 计算面积:利用中位线将大三角形分割成三个小三角形,可以计算出大三角形的面积。
三、中线与中位线的关系1. 中线和中位线的共点:三角形的中线和中位线都经过三角形的重心,即共点于重心。
2. 中线与中位线的比例关系:a. 在任意三角形中,重心到顶点的距离与重心到中点的距离之比是2:1。
b. 重心到中位线的交点的距离与重心到顶点的距离之比也是2:1。
综上所述,初中数学中关于三角形的中线与中位线的知识归纳如上。
全等三角形判定的方法(培优)
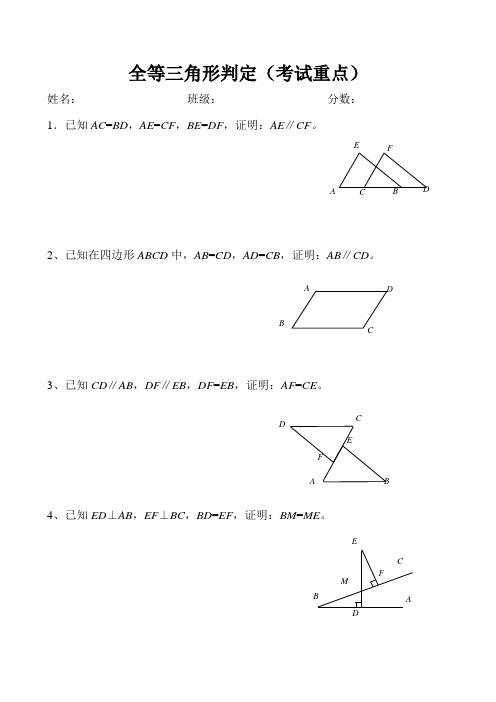
全等三角形判定(考试重点)姓名: 班级: 分数: 1.已知AC =BD ,AE =CF ,BE =DF ,证明:AE ∥CF 。
2、已知在四边形ABCD 中,AB =CD ,AD =CB ,证明:AB ∥CD 。
3、已知CD ∥AB ,DF ∥EB ,DF =EB ,证明:AF =CE 。
4、已知ED ⊥AB ,EF ⊥BC ,BD =EF ,证明:BM =ME 。
ACBDEFBADC EF BAC M EFBD5、点C 是AB 的中点,CD ∥BE ,且CD =BE ,证明:∠D =∠E 。
6、在⊿ABC 中,高AD 与BE 相交于点H ,且AD =BD ,证明:⊿BHD ≌⊿ACD 。
7已知AD =AE ,∠B =∠C ,证明:AC =AB 。
8、已知CE ⊥AB ,DF ⊥AB ,CE =DF ,AE =BF ,证明:⊿CEB ≌⊿DF A 。
ABCE HD ADEBCBACDEFD A ECB 129、如图:在△ABC 中,∠C=90°,AC=BC ,过点C 在△ABC 外作直线MN ,AM ⊥MN 于M ,BN ⊥MN 于N 。
求证:MN=AM+BN 。
10、已知,AC ⊥CE ,AC =CE , ∠ABC =∠DEC =900,求证:BD =AB +ED 。
11、已知AD 是⊿ABC 的中线,BE ⊥AD ,CF ⊥AD ,求证:BE =CF 。
12、已知∠BAC =∠DAE ,∠1=∠2,BD =CE ,求证:ABD ≌⊿ACE 。
NMCBAABCDEABCD FEADEBC12【知识点梳理】知识点一:全等三角形的概念——能够完全重合的两个三角形叫全等三角形.知识点二:全等三角形的性质.(1)全等三角形的对应边相等. (2)全等三角形的对应角相等.知识点三:判定两个三角形全等的方法.(1)SSS (2)SAS (3)ASA (4)AAS (5)HL(只对直角三形来说)知识点四:寻找全等三形对应边、对应角的规律.①全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.②全等三角形对应边所对的角是对应角,两个对应边所夹的角是对应角.③有公共边的,公共边一定是对应边. ④有公共角的,公共角一定是对应角.⑤有对顶角的,对顶角是对应角.⑥全等三角形中的最大边(角)是对应边(角),最小边(角)是对应边(角).知识点五:找全等三角形的方法.(1)一般来说,要证明相等的两条线段(或两个角),可以从结论出发,看它们分别落在哪两具可能的全等三角形中.(常用的办法)(2)可以从已知条件出发,看已知条件可以确定哪两个三角形相等.(3)可以从已知条件和结论综合考虑,看它们能否一同确定哪两个三角形全等.(4)如无法证证明全等时,可考虑作辅助线的方法,构造成全等三角形.知识点六:角平分线的性质及判定.(1)角平分线的性质:角平分线上的点到角两边的距离相等.(2)角平分线的判定:在角的内部到角的两边距离相等的点在角平分线上.(3)三角形三个内角平分线性质:三角形三条角平分线交于一点,且到三角形三边距离相等.知识点七:证明线段相等的方法.(重点)(1)中点性质(中位线、中线、垂直平分线)(2)证明两个三角形全等,则对应边相等(3)借助中间线段相等.知识点八:证明角相等的方法.(重点)(1)对顶角相等;(2)同角或等角的余角(或补角)相等;(3)两直线平行,内错角相等、同位角相等;(4)角平分线的定义;(5)垂直的定义;(6)全等三角形的对应角相等;(7)三角形的外角等于与它不相邻的两内角和.。
直角三角形中线、中位线的性质PPT课件

1 求证:CD = AB 2
证明:延长CD到E使DE=CD, 连结AE、BE. ∵AD = BD , DE =CD ∴四边形ACBE是平行四边形 又∵∠ACB = 90° ∴ □ACBE是矩形 ∴CE = AB( ?
A
D
E
C
B
) AB
1 由于CD= 2
CE
1 所以CD = 2
简单应用
A
已知△ABC是Rt△,∠ABC=Rt∠, BD是斜边AC上的中线
A
E
F
B
C
2
THANK
YOU
SUCCESS
•
三角形中位线定理:
有何作用?
三角形的中位线平行于三角形的第三 边,且等于第三边的一半。
A
D
E
符号语言: ∵DE是△ABC的中位线, ( ∵AD=BD, AE=CE )
B
C
1 ∴DE∥BC且DE= BC 2
这个定理提供了证明线段平行以及 线段成倍分关系的根据.
A
1 DE // BC =2
O
E
DE // GF
∴四边形DGFE是□
=
B
G
F
C
1、证明平行的定理有哪些?
同位角相等、内错角相等、同旁内角互补两直线平行 平行于同一直线、垂直于同一直线的两直线平行 平行四边形(矩形、菱形、正方形)的对边平行 三角形的中位线平行第三边
2、证明线段二倍关系定理有哪些?
30度所对直角边是斜边的一半 三角形的中位线等于第三边的一半 直角三角形斜边上的中线等于斜边的一半.
1、探索并掌握“直角三角形斜边上的中线性质定理” 2.理解中位线概念,明确中线与中位线的 区别与联系; 3、探索并掌握“三角形的中位线定理” 4、进一步理解转化思想(线段的倍分 要转化为相等问题来解决).
八年级数学三角形中位线培优专题训练

八年级数学三角形中位线培优专题训练一、内容提要1. 三角形中位线平行于第三边,并且等于第三边的一半。
梯形中位线平行于两底,并且等于两底和的一半。
2. 中位线性质定理的结论,兼有位置和大小关系,可以用它判定平行,计算线段的长度,确定线段的和、差、倍关系。
3. 运用中位线性质的关键是从出现的线段中点,找到三角形或梯形,包括作出辅助线。
4. 中位线性质定理,常与它的逆定理结合起来用。
它的逆定理就是平行线截比例线段定理及推论,①一组平行线在一直线上截得相等线段,在其他直线上截得的线段也相等 ②经过三角形一边中点而平行于另一边的直线,必平分第三边 ③经过梯形一腰中点而平行于两底的直线,必平分另一腰 5. 有关线段中点的其他定理还有: ①直角三角形斜边中线等于斜边的一半②等腰三角形底边中线和底上的高,顶角平分线互相重合 ③对角线互相平分的四边形是平行四边形 ④线段中垂线上的点到线段两端的距离相等 因此如何发挥中点作用必须全面考虑。
二、例题例1. 已知:△ABC 中,分别以AB 、AC 为斜边作等腰直角三角形ABM 和CAN ,P 是BC 的中点。
求证:PM =PN证明:作ME ⊥AB ,NF ⊥AC ,垂足E ,F ∵△ABM 、△CAN 是等腰直角三角形∴AE =EB=ME ,AF =FC =NF ,根据三角形中位线性质 PE =21AC =NF ,PF =21AB =MEPE ∥AC ,PF ∥AB∴∠PEB =∠BAC =∠PFC 即∠PEM =∠PFN∴△PEM ≌△PFN ∴PM =PN例2.已知△ABC 中,AB =10,AC =7,AD 是角平分线,CM ⊥AD 于M ,且N 是BC 的中点。
求MN 的长。
分析:N 是BC 的中点,若M 是另一边中点, 则可运用中位线的性质求MN 的长, 根据轴称性质作出△AMC 的全等三角形即可。
辅助线是:延长CM 交AB 于E (证明略 例3.如图已知:△ABC 中,AD 是角平分线,BE =CF ,M 、N 分别是BC 和EF 的中点 求证:MN ∥AD 证明一:连结EC ,取EC 的中点P ,连结PM 、PNP NMP ∥AB ,MP =21AB ,NP ∥AC ,NP =21AC ∵BE =CF ,∴MP =NP∴∠3=∠4=2MPN-180∠∠MPN +∠BAC =180(两边分平行的两个角相等或互补)∴∠1=∠2=2MPN-180∠ , ∠2=∠3∴NP ∥AC ∴MN ∥AD证明二:连结并延长EM 到G ,使MG =ME 连结CG ,FG则MN ∥FG ,△MCG ≌△MBE ∴CG =BE =CF ∠B =∠BCG∴AB ∥CG ,∠BAC +∠FCG =180∠CAD =21(180-∠FCG ) ∠CFG =21(180-∠FCG )=∠CAD ∴ MN ∥AD 例4. 已知:△ABC 中,AB =AC ,AD 是高,CE 是角平分线,EF ⊥BC 于F ,GE ⊥CE交CB 的延长线于G 求证:FD =41CG 证明要点是:延长GE 交AC 于H , 可证E 是GH 的中点过点E 作EM ∥GC 交HC 于M ,则M 是HC 的中点,EM ∥GC ,EM =21GC由矩形EFDO 可得FD =EO =21EM =41GC三、练习1. 如图11,M 、P 分别为△ABC 的AB 、AC 上 的点,且AM=BM ,AP=2CP ,BP 与CM 相交于N ,已知PN=1,则PB 的长为 ( ) A. 2 B. 3 C .4 D. 52. 如图12,△ABC 中,∠B =2∠C ,AD ⊥BC 于D ,M 为BC 的中点,AB=10,则MD 的长为 ( )A. 10B. 8 C .6 D. 53. 如图13,△ABC 是等边三角形,D 、E 、F 分别是AB 、BC 、AC 的中点,P 为不同于B 、E 、C 的BC 上的任意一点,△DPH 为等边三角形.连接FH ,则EP 与FH 的大小关系是 ( ) A. E P>FH B. EP=FH C. EP<FH D.不确定4. 如图14,在△ABC 中,AD 平分∠BAC ,BD ⊥AD ,DE ∥AC ,交AB 于E ,若AB=5,则DE 的长为 .C5. 如图15,△ABC中,AB=4,AC=7,M为BC的中点,AD平分∠BAC,过M作MF∥AD,交AC于F,则FC的长等于.6. 如图25,P为△ABC内一点,∠P AC=∠PBC,PM⊥AC于M,PN⊥BC于N.D是AB的中点.求证:DM=DN7. 如图16,在△ABC中,D、E是AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点,直线MN分别交AB、AC于P、Q.求证:AP=AQ8. 如图17,BE、CF是△ABC的角平分线,AN⊥BE于N,AM⊥CF于M.求证:MN∥BC.9. 如图18,在△ABC中,AD平分∠BAC,AD=AB,CM⊥AD于M.求证:AB+AC=2AM10.如图19,四边形ABCD中,G、H分别是AD、BC的中点,AB=CD.BA、CD的延长线交HG的延长线于E、F.求证:∠BEH=∠CFH.1. 如图20,在△ABC中,∠ABC=2∠C,AD平分∠BAC,过BC的中点M作ME⊥AD,交BA的延长线于E,交AD的延长线于F.求证:12BE BD.2. 如图21,在△ABC中,AB<AC,P为AC上的点,CP=AB,K为AP的中点,M为BC的中点,MK的延长线交BA的长线于N.求证:AN=AK.3. 如图22,分别以△ABC的边AC、BC为腰,A、B为直角顶点,作等腰直角△ACE和等腰直角△BCD,M为ED的中点.求证:AM⊥BM.4. 如图23,点O是四边形ABCD内一点,∠AOB=∠COD=1200,AO=BO,CO=DO,E、F、G分别为AB、CD、BC的中点.求证:△EFG为等边三角形.5. 如图24,△ABC中,M是AB的中点,P是AC的中点,D是MB的中点,N是CD的中点,Q是MN的中点,直线PQ交MB于K.求证:K是DB的中点.6. 如图25,P为△ABC内一点,∠P AC=∠PBC,PM⊥AC于M,PN⊥BC于N.D是AB的中点.求证:DM=DN图21 图22 图23 图24 图257. 如图26,AP是△ABC的角平分线,D、E分别是AB、AC上的点,且BD=CE.又G、H分别为BC、DE的中点.求证:HG∥AP.8. 如图27,已知△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=900,如图(a),连接DE,设M为DE的中点.(1)求证:MB=MC;(2)设∠BAD=∠CAE,固定△ABD,让Rt△ACE绕顶点A在平面内旋转到图(b)的位置,试问MB=MC是否成立?并证明其结论.9. 已知△ABC面积为S,作直线l∥BC,交AB于D,交AC于E,若△BED的积为K.求证:S≥4K.10.如图28,在△ABC中,AB=AC,D是BC边上的一点,E是线段AD上的一点.且∠BED=2∠CED=∠BAC.求证:BD=2CD.图26 图27。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直角三角形斜边上的中线的应用
知识储备:直角三角形斜边上的中线等于斜边的一半.
根据这个性质可知,直角三角形被分割成两个顶角互补、底角互余的等腰三角形.灵活运用此性质在解答一些与中点或中线有关的问题时,常能收到事半功倍之效.
例1 如图1,已知△ABC中,∠ACB=90°,OA=OC,求证:OB=OC
基本结论:①若OA=OB,则OA=OB=OC, ②若OA=OC,则OB=OC,③若OB=OC,则OA=OC.
例2(1)如图1,已知△ABC和△ABD中,∠ACB=∠ADB=90°,点O是AB的中点,求证:OC=OD (2)在上述条件下,如图2,(1)中结论还成立吗?为什么?
基本结论:若OA=OB,则OA=OB=OC=OD
例3 如图,∠DBC=∠BCE=90°,M为DE的中点,求证:MB=MC
D
E 例4 如图,在△ABC中,AB=AC,∠ABC=90°,点E,F分别在AB,AC上,且AE=EF,点O,M分别为
AF,CE的中点,求证:(1)OM
=1
2
CE;(2)OB
例5 如图,△ABC中,AB=AC,∠ABD=∠CBD. DE⊥BD,DE交BC于E.求证:CD=
1
2
BE
.
例6 如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,点M,N分别是BC,DE的中点,
(1)求证:MN⊥DE;(2)连ME,MD,若∠A=60°,求
MN
DE
的值
.
例7 △BCD和△BCE中,∠BD C=∠BEC=90°,O为BC的中点,BD,CE交于A,
(1)如图1,若∠BAC=120°,求证:DE=OE.
(2)如图2,若∠BAC=135°,求证:DE.
(3)若∠BAC=α,则∠EOD的度数为.(用α表示)
图1 图2
图1 图2
构造三角形中位线
知识储备:三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
这个定理的特点是:同一题设下,有两个结论,一个结论表明位置关系,另一个结论表明数量关系.应用这一定理时,不一定同时用到两个结论,有时用到平行关系,有时用到倍分关系.常用构造三角形中位线的方法处理中点问题.
题型一 利用角平分线和垂直构造中位线
例1 如图,在△ABC 中,AB =BC ,∠ABC =90°,F 为BC 上一点,M 为AF 的中点,BE 平分∠ABC ,且EF ⊥BE ,求证:CF =2ME .
题型二 倍长构造三角形中位线
例2如图,在△ABC 中,∠ABC =90°,BA =BC ,△BEF 为等腰直角三角形,∠BEF =90°,M 为AF 的中
点,求证:ME =1
2
CF
题型三 取中点构造三角形中位线
例3 如图,在△ABC 中,∠C =90°,CA =CB ,E ,F 分别为CA ,CB 上的一点,CE =CF ,M
,N 分别为AF ,BE 的中点,求证:AE .
F
题型四 连接两点构造三角形中位线
例4 如图,在△ABC 中,∠B =2∠A ,CD ⊥AB 于D , 点E ,F 分别为AB ,BC 的中点.求证:DE =DF
A
例5 已知∠ACB =∠BCD =90°,AC =BC ,CD =CE .
(1)如图1,AE 与BD 的大小关系为 ,位置关系为 .
(2)如图2,点P ,M ,N 分别为AB ,AD ,BE 的中点,试探究:PM 与PN 之间的数量关系和位置关系; (3)将图2中的△CDE 绕点C 旋转至如图3所示的位置,其余条件不变,则MN 与PN 的数量关系
为 .
图1
图3
图2
例7 如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M是BC的中点.求证:AB=2DM.
例5 如图,在Rt△ABC中,∠C=90°.AD∥BC,∠ABE=2∠CBE.求证:DE=2AB.
(提示:取DE的中点F,连接AF)
D B。
