大学物理上 章节小结
大学物理上册重点小结
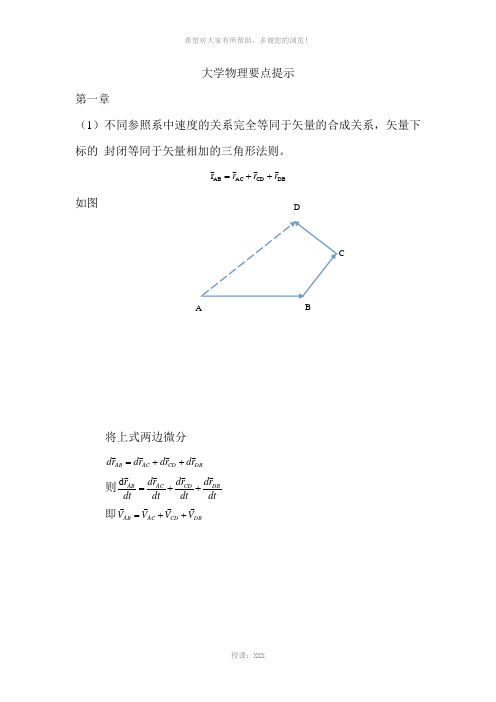
大学物理要点提示第一章（1）不同参照系中速度的关系完全等同于矢量的合成关系，矢量下标的 封闭等同于矢量相加的三角形法则。
DB CD AC AB r r r r ++=如图将上式两边微分DB CD AC AB r d r d r d r d ++=则dt r d dt r d dt r d dt r DB CD AC AB++=d 即DB CD AC AB V V V V ++=ABCD第二章由于有运动的绝对性和相对性，所以牛顿第二定律的出现就伴随着非惯性系的出现。
并且牛顿第一定律就是针对惯性系成立的，当物体的运动轨迹是空间的固定曲线时，就用自然坐标系描述，此时它的加速度有切向分量和法向分量。
在求解牛顿方程时，一定要使方程两边各有一个变量：如kx dtdvm -=一定要将dt dv 变成v dx dv •又KQ dtdw m=要将dt dw变成W dQ dW dt dQ dQ dW =•第三章1.必须记住w 与转向的关系，这样就能记住F r M⨯=的定义理由由td v d m F =两边叉乘r则dt r d dt v d m r F r )(ρ⨯=⨯=⨯即dtW d J dt L d M ==2.要充分利用转动惯性量的平行轴定理和垂直轴定理。
3.计算转动惯量就是要找出dJ 与dm r i 2的关系，尤其是i i r dm 与的关系。
依次类推 面计算dq dE dq du 与，与的关系时，也是找出i r dq 与的关系。
第四章1.伽利略变换是洛仑兹变换的极限情况，因此用伽利略变换可帮助辨析洛仑兹变换的正确性。
2.在相对论中的“长度缩短”和“时钟延缓”都只具有相对意义，即B看到或感到A的“长度缩短”或“时钟延缓”A也会看到或感到B 的“长度缩短”和“始终延缓”。
第五章电偶极子形成的电场304r p E πε -= l q p=l是从负电荷指向正电荷并l r ∝高斯定理⎰∑=0εqs d ES 外的q 对s d E •⎰无贡献，但对某处的E仍有贡献。
大学物理各篇小结(上部)
衍射现象
光波遇到障碍物或通过小孔时，光波的传播方向会发生改变，形 成明暗相间的衍射条纹。
衍射分类
根据产生衍射的原因，可分为菲涅尔衍射和夫琅禾费衍射。
衍射公式
根据菲涅尔衍射公式，当衍射角θ=0时，衍射光强最大；当 θ=±π/2时，衍射光强最小。
光的偏振
01
02
03
偏振现象
光波的电矢量或磁矢量在 某一特定方向上振动，这 种现象称为光的偏振。
干涉现象
当两束或多束相干光波在空间 某一点叠加时，光波的振幅会 相加，形成明暗相间的干涉条
纹。
干涉条件
相干光波、有恒定的相位差、 有相同的振动方向、有相同的
频率。
干涉公式
光强与相位差有关，当相位差 为2nπ（n为整数）时光强最
大，为Imax；相位差为 (2n+1)π时光强最小，为Imin。
光的衍射
详细描述
弹性力学是研究物体在受力时如何发生形变和应力分布的学科。它涉及到弹性材料的性质、应力和应 变的关系、弹性形变的计算方法等。弹性力学在工程领域有着广泛的应用，如建筑、机械、航空航天 等领域的结构设计都需要考虑弹性力学原理。
02 热学篇小结
热力学基础
总结词
热力学基础是研究热现象的宏观规律的科学，主要涉及温度、热量、熵等基本 概念。
交流电与电磁波
交流电与电磁波是电磁学中的重要应用，它们在电力传输 、无线通信等领域具有广泛的应用。
交流电是指电流方向随时间周期性变化的电流，广泛应用 于电力系统。电磁波是指交替变化的电场和磁场，以波的 形式传播能量。无线通信、电视信号传输和雷达等应用都 基于电磁波的传播特性。
04 光学篇小结
光的干涉
详细描述
大学物理第1-4章经典力学部分归纳总结
应用
机械能守恒定律可以用于解决一些简单的运动学问题， 如自由落体、抛体运动等。
05 万有引力定律
万有引力定律的发现与意义
发现
牛顿通过观察苹果落地等现象，发现 了万有引力定律。
意义
万有引力定律揭示了自然界中物体之 间的相互作用规律，为经典力学的发 展奠定了基础。
万有引力定律的内容与公式
内容
任意两个质点之间都存在相互吸引的力，大小与两质点质量的乘积成正比，与它们之间距离的二次方成反比。
经典力学与许多其他学科领域密切相关， 如材料科学、工程学和天文学等，鼓励学 生在跨学科应用中拓展知识。
关注前沿研究
实践与实验
了解经典力学在前沿科学研究中的应用， 关注最新研究成果和技术进展。
通过实验和实践巩固理论知识，提高动手 能力和实验技能。
THANKS FOR WATCHING
感谢您的观看
工作原理等。
04 能量与动量定理
能量定义与计算
要点一
定义
能量是物体做功的能力，可以表示为系统动能和势能之和 。
要点二
计算
能量可以用数学公式进行计算，如动能公式 (E_k = frac{1}{2}mv^2)，势能公式 (E_p = mgh) 等。
动量定理与冲量
定理
动量 (p = mv) 是物体质量和速度的乘积，冲量 (I = Delta p) 是动量的变化量。
03
经典力学在日常生活和工程应用中有着广泛的应用，如车辆 运动、机械运转、天体运动等。
章节概览
第1章
牛顿运动定律
第3章
能量和力做功
第2章
动量和角动量
第4章
万有引力和相对论基础
02 牛顿运动定律
大学物理一、二、三、四章小结
(3) 了解：*经典力学的成就和局限性。
8
(2) 理解：冲量的概念；质点和质点系的动量。
(3) 了解：系统内质量移动问题。
2、能量守恒定律 (1) 掌握：变力作功的计算；动能定理；功能原理；机 械能守恒定律；能量守恒定律；质心运动定律。 (2) 理解：保守力与非保守力；保守力作功；势能；完 全弹性碰撞；完全非弹性碰撞。 (3) 了解：质心；势能曲线。
一、二、三、四章小结
1
第一章 质点运动学小结
1、质点运动的描述 (1)掌握：位矢、位移、速度、加速度等物理量的定义及
表达式，能够从已知的运动方程求导得到速度、加速度；
同时能够从已知的速度或加速度积分得出运动方程。
(2) 理解：位矢、位移、速度、加速度的“矢量性”和
“瞬时性”，会计算位矢、位移、速度、加速度等的各
一、牛顿运动定律的适用范围
1. 惯性系内，低速运动; 2. 宏观问题。 二、质点动力学问题的类型 1.已知作用于质点的力, 求质点的运动情况； 2.已知质点的加速度，求作用于质点的力； 3.已知质点的某些力和运动学条件，求质点所受的另
一些力和质点的运动情况。
5
三、应用牛顿定律解题的一般步骤 1. 选定惯性参考系和可看作质点的隔离体作为研究对
(2)理解：运动的相对性和独立性。
3
第二章 牛顿定律小结
(1) 掌握：牛顿定律及其适用条件，牛顿定律的应用。 (2) 理解：惯性、质量和力的概念；力的叠加原理；力 学相对性原理；物理量的单位和量纲。 (3) 了解：几种常见的力 ( 万有引力、弹性力、摩擦力 ) ；
非惯性系、惯性力。
4
牛顿运动定律的应用
象；
2.分析受力情况画出受力图(找出全部力);
00-大学物理教程上册各章内容小结
动量的增量 。
t2 t1
F exdt
n i 1
mi vi
n i 1
mi vi0
二. 质点系动量守恒定律
质点系所受合外力为零，系统总动量守恒。即
若
Fiex 0
则p
pi
常矢量
i
i
➢ 说明： 1. 守恒条件：合外力为零，或外力<< 内力；
2. 某一方向合外力为零，则该方向 pix const.
2 质心运动定理: 作用在系统上的合外力等于系统的总质量 乘以质心的加速度
四 质点的角动量 角动量守恒定律
质点相对于点O的角动量：
L
r
p
r
m
v
角动量大小： L rp sin mrv sin
当W ex
W in nc
0
时，有
E
E0
第4章 动量和角动量
质一点. 的动动量量、冲p量、m动v量定理——机械运动的量度
力的冲量 I
t2
Fdt
——力对时间的累积
t1
质点的பைடு நூலகம்量定理：质点所受合外力的冲量等于质点在此时
间内动量的增量 。
t2 t1
Fdt
mv2
mv1
质点系的动量定理：系统所受合外力的冲量等于系统
3、势能是属于系统的 ；
➢ 力学中常见的势能
重力势能 Ep mgh
弹性势能
Ep
1 kx2 2
引力势能
Ep
G
m' m r
四. 功能原理、机械能守恒定律
➢ 质点系的功能原理：质点系机械能的增量等于外力和 非保守内力作功之和 .
Aex
Ain nc
大物章节总结知识点
大物章节总结知识点第一章：力学基础1.1 研究对象及基本概念物理学研究的对象是宇宙中的物质和运动，力学是研究物体的运动的一门物理学科。
物体是指占据空间、具有质量的物质。
运动是指物体在空间中的位置随时间发生的变化。
在力学中，物理量包括质量、力、速度、加速度、位移等。
1.2 物体运动的描述运动是在一定空间和时间内物体位置的变化。
运动状态的描述需要考虑时间和位置两个因素。
在力学中，常用的描述方法有坐标系、时刻、位移、速度、加速度等。
1.3 物体运动的规律牛顿三定律是描述物体运动规律的基础。
第一定律表明，物体要么处于静止状态，要么以匀速直线运动；第二定律指出，物体的加速度与作用在其上的力成正比，与质量成反比；第三定律说明，两个物体相互作用时，彼此施加的作用力大小相等，方向相反。
第二章：动力学2.1 力的概念力是导致物体发生运动或形状变化的原因。
力是一个矢量，包括大小和方向两个方面。
常见的力有重力、弹力、摩擦力、张力等。
2.2 牛顿运动定律牛顿运动定律是经典力学的基石。
第一定律，即惯性定律，指出物体的静止或匀速直线运动状态不会自发改变；第二定律，即运动定律，描述了物体受力时加速度的变化规律；第三定律，即作用与反作用，阐明了物体间作用力的相互影响。
2.3 力的合成与分解如果一个物体受到多个力的作用，则其合力可以用力的合成法则求得。
力的分解指的是将一个力分解成两个分力的过程。
2.4 动能和动能定理动能是描述物体运动状态的物理量，它与物体的质量和速度相关。
动能定理指出，外力对物体做功会使物体的动能发生改变。
2.5 势能与机械能守恒势能是物体由于位置或状态而具有的能量，常见的势能有重力势能、弹性势能等。
机械能守恒定律指出，在没有其他非弹性因素作用时，系统的机械能保持不变。
第三章：动力学应用3.1 运动的描述位置、速度、加速度等描述运动的基本物理量。
在一维直线运动中，运动规律可以用直线方程描述。
3.2 牛顿定律的应用应用牛顿第二定律可以计算物体在受力情况下的加速度。
各章总结大学物理上
E 外表面附近
0 不同与无限大带电平面电场
（3）孤立导体静电平衡后，表面各处的电荷面密度
与曲率有关，曲率越大，σ越大。（如尖端放电现象）
前页 后页 目录 11
三、空腔导体和静电屏蔽
1、空腔导体内无带电体
——无论空腔导体本身是否带电，也无论空腔导体外是否有带电体， 可以证明，静电平衡时，空腔导体：
RB RA
真空中孤立导体球
C 40R
前页 后页 目录 14
电容器的串联和并联
串联： 1 1 1 1
C C1 C2
Cn
并联： C C1 C2 Cn
五、静电场的能量 (1)电容器的电场能量
We 1 Q2 1 CU 2 1 QU
2C 2
2
(2)所有静电场的能量 W
V wedV
i
dΦ dt
d dt
S
B dS
前页 后页 目录 19
感生电动势 1)利用法拉第电磁感应定律计算（常用）
2）用感 E感 d l 计算（不常用）
2、自感和互感
自感电动势
L
L
dI dt
自感系数 L dΦN ΦN dI I
螺线管的自感系数 L 0n2V
前页 后页 目录 20
互感电动势
21
M 21
2)安培环路定理 L B d l 0 I内
适用于对称性磁场
前页 后页 目录 16
磁场复习 2、磁场的性质
1)磁场的高斯定理 S B d S 0
稳恒磁场是无源场
2)安培环路定理 L B d l 0 I内
稳恒磁场是有旋场 （非ห้องสมุดไป่ตู้守场）
3、磁场的特点 1)对运动电荷 F
q
物理必修三前两章知识点总结
物理必修三前两章知识点总结第一章静电场。
一、电荷及其守恒定律。
1. 电荷。
- 自然界中存在两种电荷：正电荷和负电荷。
丝绸摩擦过的玻璃棒带正电，毛皮摩擦过的橡胶棒带负电。
- 电荷的多少叫电荷量，用Q或q表示，单位是库仑，简称库，符号是C。
2. 电荷守恒定律。
- 电荷既不能被创造，也不能被消灭，只能从一个物体转移到另一个物体，或者从物体的一部分转移到另一部分；在转移的过程中，电荷的总量保持不变。
- 三种起电方式：摩擦起电、感应起电和接触起电。
- 摩擦起电：两个物体相互摩擦时，束缚电子本领弱的物体的一些电子转移到束缚电子本领强的物体上，原来呈电中性的物体由于得到电子而带负电，失去电子的物体带正电。
- 感应起电：当一个带电体靠近导体时，由于电荷间的相互吸引或排斥，导体中的自由电荷便会趋向或远离带电体，使导体靠近带电体的一端带异种电荷，远离带电体的一端带同种电荷。
这种现象叫做静电感应，利用静电感应使金属导体带电的过程叫感应起电。
- 接触起电：一个不带电的导体跟另一个带电的导体接触后分开，使不带电的导体带上电荷的方式。
二、库仑定律。
1. 内容。
- 真空中两个静止点电荷之间的相互作用力，与它们的电荷量的乘积成正比，与它们的距离的平方成反比，作用力的方向在它们的连线上。
2. 表达式。
- F = k(q_1q_2)/(r^2)，其中k = 9.0×10^9N· m^2/C^2，叫做静电力常量。
- 适用条件：真空中、静止的点电荷。
点电荷是一种理想化模型，当带电体间的距离比它们自身的大小大得多，以致带电体的形状、大小及电荷分布状况对它们之间相互作用力的影响可以忽略不计时，这样的带电体就可以看成点电荷。
三、电场强度。
1. 电场。
- 电荷的周围存在着电场，电场是一种客观存在的特殊物质，电场的基本性质是对放入其中的电荷有力的作用。
2. 电场强度。
- 定义：放入电场中某点的电荷所受的电场力F与它的电荷量q的比值，叫做该点的电场强度，简称场强。
大学物理上册知识点总结整理及复习纲要
《大学物理》上册知识点整理及复习纲要第一章质点运动学一、基本要求：1、熟悉掌握描述质点运动的四个物理量一一位置矢量、位移、速度和加速度。
会处理两类问题：（1）已知运动方程求速度和加速度；（2）已知加速度和初始条件求速度和运动方程。
2、掌握圆周运动的角速度、角加速度、切向加速度和法向加速度。
二、内容提要:1、位置矢量：r xi y j zk2 2 2位置矢量大小：r x y zx 位置矢量方向：COSr 3、位移r ：r xi yj zk6、圆周运动: 角位置角位移d角速度cos cos2、运动方程：位置随时间变化的函数关系r(t) x(t)i y(t) j z(t)k 无限小位移： d r dxi dy j dzk4、速度：平均速度:瞬时速度: dx■Idtdy dz5、加速度：瞬时加速度:dvxi dtdVydt) dt dtdvzkdt dt2d y2dt2d z2 kdtdt2 dd角加速度2dt dt基本要求： 1、 、 理解牛顿定律的基本内容； 2、 熟练掌握应用牛顿定律分析问题的思路和解决问题的方法。
解一维变力作用下的简单动力学问题。
内容提要： 1 、 牛顿第一定律 3、 牛顿第二定律 : F m a F 指合外力 a 合外力产生的加速度 在直角坐标系中：4、 牛顿第三定律 : F F ' 三、 力学中常见的几种力在自然坐标系中：a an at2 v dv en et rdt7、匀加速直线运动与匀角加速圆周运动公式比较：v v0 at 12 x v0t at 2 22 v v02ax三、 解题思路与方法： 各坐标轴的分量； 初始条件，通过积分的方法求速度和运动方程，积分时应注意上下限的确定。
质点运动学的第一类问题：已知运动方程通过求导得质点的速度和加速度，包括它沿 质点运动学的第二类问题：首先根据已知加速度作为时间和坐标的函数关系和必要的第二章牛顿定律0tt2 02能以微积分为工具， 求F x max F y 在曲线运动中应用自然坐标系 : 2 v F n man mrmay F z maz dvF t mat m dtkx 弹性力与位移成反向 接触面上有滑动或相对滑动趋势产生的一1、、重力: mg2、弹性力: 弹簧中的弹性力 F3、摩擦力：摩擦力指相互作用的物体之间，种阻碍相对滑动的力，其方向总是与相对滑动或相对滑动的趋势的方向相反。
大学物理大一知识点总结笔记大全
大学物理大一知识点总结笔记大全第一章线性运动1.1 位置、位移和速度在物理学中，我们通常使用位置、位移和速度这三个概念来描述物体的运动。
位置是指物体所处的空间位置，位移是指物体从初始位置到结束位置的变化量，速度是指物体单位时间内位移的大小。
1.1.1 位置的表示在一维情况下，我们可以用实数轴上的一个坐标来表示物体的位置。
在二维或三维情况下，我们可以使用坐标系来表示位置。
1.1.2 位移和速度的关系位移是一个矢量量，它有大小和方向。
速度则是位移的导数，表示单位时间内位移的变化率。
速度的大小可以用平均速度和瞬时速度来描述。
1.2 加速度和速度的变化1.2.1 加速度的概念加速度是速度的变化率，表示单位时间内速度的变化量。
1.2.2 加速度和速度的关系在匀变速运动下，速度的变化是均匀的，加速度保持不变。
在非匀变速运动下，速度的变化不是均匀的，加速度可能会变化。
1.3 物体的简谐振动1.3.1 简谐振动的定义简谐振动是指物体围绕平衡位置做周期性振动的运动。
1.3.2 简谐振动的特点简谐振动的特点包括振幅、周期、频率和相位等。
第二章力学2.1 牛顿定律2.1.1 牛顿第一定律牛顿第一定律也被称为惯性定律，它描述了在没有外力作用时物体将保持静止或匀速直线运动的状态。
2.1.2 牛顿第二定律牛顿第二定律描述了物体在受力作用下产生加速度的关系，力等于物体的质量乘以加速度。
2.1.3 牛顿第三定律牛顿第三定律描述了物体之间相互作用的力是大小相等、方向相反的。
2.2 动能和势能2.2.1 动能的定义和计算动能是指物体由于运动而具有的能量，它的大小与物体的质量和速度相关。
2.2.2 劢能定理动能定理描述了物体受到的外力做功等于其动能的变化量。
2.2.3 势能的定义和计算势能是指物体由于位置而具有的能量，常见的势能有重力势能和弹性势能等。
2.3 弹性碰撞和不可恢复碰撞2.3.1 弹性碰撞的定义和特点弹性碰撞是指两个物体发生碰撞后能够完全弹开并保持动能守恒的碰撞。
(完整版)大学物理知识点总结
Br ∆A rB ryr ∆第一章质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r 称为位矢 位矢r xi yj =+,大小 2r r x y ==+运动方程()r r t =运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆△，2r x =∆+△路程是△t 时间内质点运动轨迹长度s ∆是标量。
明确r ∆、r ∆、s ∆的含义(∆≠∆≠∆r r s ) 2. 速度（描述物体运动快慢和方向的物理量）平均速度xyr x y i j ij t t t瞬时速度(速度) t 0r drv limt dt∆→∆==∆(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x +=+==，2222yx v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛== ds dr dt dt= 速度的大小称速率。
3. 加速度(是描述速度变化快慢的物理量）平均加速度va t ∆=∆ 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆△ a 方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x二.抛体运动运动方程矢量式为 2012r v t gt =+分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量：线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。
大学物理各章主要知识点总结
第六、七章 电 学
描述电场性质的主要物理量是场强和电势。 本章主要研究场强和电势的计算方法。 另外还有电容器的电容及电场能量的计算。
1 几种典型带电体激发电场的重要结论和等
效情况（注意：场强是矢量）
点电荷： 无限长均匀带电直线：
E q
4
π
绝对速度 相对 牵连速度 速度
7 匀加速直线运动与匀加速圆周运动的等效
角量
x
x0
v0t
1 2
at
2
v v0 at
v2 v02 2a(x x0 )
切向量
0
0t
1 2
t2
0 t
B
3.功的基本定义式 A F dr A
注：若在直角坐标系中有
A
B A
F
dr
B A
F
dx
F
dy
F
dz
x
y
z
4 有心力功的计算：
1.有心力定义：物体受到由力心发出的力。如万有引力
2.定义式： F F(r)r0
3.特点：大小只与到力心的距离r有关，大小即F(r)
. 力的空间累积效应
r2
F
dr
r1
功、动能、动能定理、势能、机械能、
功能原理、机械能守恒定律
1 动力学问题的解题步骤： (1)确定研究对象 (2)确定参考系（默认大地，可不写） (3)建立坐标系 (4)分析物体的运动或者受力情况 (5)列方程
大学物理各章主要知识点总结
05
第五章：电磁场的基本规律
静电场
1 2
静电场的定义
电荷在空间中激发的电场，静止电荷的电场称 为静电场。
静电场的性质
高斯定理、环路定理、电场力的性质、电容和 电场的能量。
3
静电场的应用
静电场中物体的平衡、静电屏蔽、电容器的充 放电等。
恒定磁场
恒定磁场的定义
电流在空间中产生的磁场，恒定磁场与时间 无关。
开尔文表述
不可能制成一种循环动作的热机，从单一热源取 热，使之完全变为功而不引起其它变化。
卡诺循环
01
02
03
卡诺循环
卡诺循环是一种理想的热 机循环，它由两个等温过 程和两个绝热过程组成。
卡诺循环的效率
卡诺循环的效率是所有热 机效率的最高值，它等于 两个热源温度之比。
卡诺机的效率
卡诺机的效率是所有热机 效率的最高值，它等于两 个热源温度之比。
大学物理各章主要知识点总结
xx年xx月xx日
contents
目录
• 第一章：力和运动 • 第二章：能量与动量 • 第三章：振动与波 • 第四章：热力学基础 • 第五章：电磁场的基本规律 • 第六章：波动光学 • 第七章：量子物理基础 • 第八章：相对论力学基础
01
第一章：力和运动
动力学基本概念
力的概念
力是物体间的相互作用，具有 大小、方向和作用点三个要素
。
牛顿运动定律
牛顿运动定律是描述物体运动和 作用力关系的定律，包括惯性定 律、运动定律和作用与反作用定 律。
力的分类
根据力的作用方式，力可分为保守 力和非保守力；根据力的作用效果 ，力可分为汇交力和张力。
牛顿运动定律
惯性定律
物理章节知识总结归纳
物理章节知识总结归纳物理作为一门自然科学，研究物质、能量以及它们之间相互作用的规律。
在学习物理的过程中，我们会接触到各种不同的章节内容，涉及到力学、热学、光学、电磁学等多个方面。
本文将对这些物理章节的知识进行总结归纳，以期帮助读者更好地理解和掌握物理学的基本原理。
一、力学章节知识总结归纳力学是研究物体运动的学科，是学习物理的基础。
它包括了质点运动学、质点动力学以及刚体力学等内容。
1. 质点运动学质点运动学是研究质点运动状态、轨迹和速度、加速度等的学科。
其中，位移、速度和加速度是描述质点运动的基本物理量。
- 位移：物体从一个位置移动到另一个位置的改变矢量。
它的大小为两个位置之间的距离，并指向移动方向。
- 速度：物体单位时间内位移的变化率。
速度的大小等于位移的大小与时间的比值，方向与位移的方向相同。
- 加速度：物体单位时间内速度的变化率。
加速度的大小等于速度的变化量与时间的比值，方向与速度的变化方向相同。
2. 质点动力学质点动力学是研究质点运动的原因和规律的学科。
其中，牛顿三定律是描述质点运动的基本原理。
- 第一定律（惯性定律）：物体静止或匀速直线运动时，受力为零。
- 第二定律（运动定律）：物体在受力作用下会产生加速度，其大小与作用力成正比，与物体质量成反比。
- 第三定律（作用-反作用定律）：任何两个物体之间都存在着大小相等、方向相反的两个力，且这两个力作用在不同的物体上。
3. 刚体力学刚体力学是研究刚体平衡和运动的学科，它是力学中一个重要的分支。
平衡条件和力矩是刚体力学的核心内容。
- 刚体平衡条件：一个刚体处于平衡状态时，对刚体施加的外力和外力矩的合力和合力矩均为零。
- 力矩：力矩是描述力对物体产生转动效果的物理量。
力矩的大小等于力的大小与力臂（力对应直线距离物体转轴的距离）的乘积，方向遵循右手螺旋法则。
二、热学章节知识总结归纳热学是研究物体热现象和热力学性质的学科，它包括了热力学、热传导、热辐射等内容。
大学物理(上册总结)
碰撞
(两个或多个物体相遇,物体间相互作用仅持续 极为短暂的时间)
完全弹性碰撞
动量守恒 动能守恒
非完全弹性碰撞 完全非弹性碰撞
动量守恒
动能不守恒 动量守恒 动能不守恒
碰后有共同速度
刚体内容小 结
力和力矩的瞬时效应
牛顿第二运动定律：
F ma
刚体定轴转动的转动定律：
M J
力和力矩的空间积累效应
m ax may
m dvx dt
m dv y dt
mmdddd2t2t2x2y
Fz
maz
m dvz dt
d2z m dt 2
自然坐标系
Fn
ma n
2
m R
F
m a
m d（平面）
dt
解题类型:
由:
F ma
a r
(1). 已知：F、m 运动
1 2
J 2 2
力的时间积累效应
１、质点的动量定理
t2 t1
Fdt
P2
P1
P
2、质点系的动量定理
tt12F外dt
P2
P1
P
3、动量守恒定律
守恒条件： F外 0 P2 P1 适用于质点系。
力矩的时间积累效应
1、角动量 质点的角动量
可应用于任 何一个分量
Fx 0 Px 常矢量 Fy 0 Py 常矢量
Fz 0 Pz 常矢量
3、熟练掌握功的定义即变力做功的计算方法，深入理解
质点系的动能定理及计算。
大学物理上-章节小结
第一章 质点运动的描述 小结一、运动学特点：瞬时性、矢量性、相对性。
二、基本概念：1、位矢：k z j y i x r++=位矢大小：222z y x r r ++==r方向：由坐标原点指向质点。
2、速度：j v i v j dtdy i dt dx dt r d v y x+=+==v的大小：2y 2x 22v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛==v的方向：所在位置的切线向前方向。
3、速率：dtdsv v ==4、加速度：j a i a j dt y d i dt x d j dt dv i dt dv dt v d a y x 2222y x +=+=+==a的大小：2222222y 2x 2y 2x dt y d dt x d dt dv dt dv a a a ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+= 或自然坐标系中，n n t t t t e a e a dte d v e dt dv dt v d a+=+==大小：2222n 2t r v dt dv a a a ⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+= 方向：tna a tg =θ三、运动描述1、运动方程：⑴矢量式：k )t (z j )t (y i )t (x )t (r++=⑵标量式：)t (x x =，)t (y y =，)t (z z = 2、轨迹方程：0)y ,x (F =3、圆周运动的角量描述：（1）角坐标 （2）角速度dtd θ=ω（3）角加速度22dt d dt d θ=ω=α 4、角量与线量的关系：①ω=r v ②α=r a t③2n r a ω=四、相对运动ME PM PE v v v +=五、运动类型1、直线运动→≡0a n ，一维情况下，标量式代替矢量式。
2、曲线运动→≠0a n第二章牛顿定律、第三章动量守恒定律和能量守恒定律 小结一、牛顿运动三定律 二、常见力①弹性力②万有引力 ：保守力 ③摩擦力 ：非保守力 三、重要物理量①动量v m P =②冲量()t F t t F dt F I t t ∆•=-==⎰1221③动能2k mv 21E =④功⎰⋅=b aS d F W合力功等于各分力功之和。
大学物理上章节小结
二、定律
转动定律 →
角动量守恒定律： , =常矢
动量守恒定律： , =常矢
三、定理
角动量定理( )→质点或质点系的动量定理
转动动能定理（ ）→质点的动能定理
第十七章狭义相对论小结
一、爱因斯坦的两个基本假设:相对性原理和光速不变原理
二、坐标变换
1、伽利略变换（经典）
2、洛伦兹变换(相对论） 或
１、定理
（1)动能定理
①质点的动能定理
②质点系的动能定理
(２）动量定理
①质点的动量定理
②质点系的动量定理
2、原理:功能原理
3、守恒定律
(1）动量守恒定律条件 ,惯性系
（２)机械能守恒条件：
第四章刚体运动小结
一、物理量
力矩 →力 角动量（ ）→动量（ ）
角速度 →速度 转动动能( )→质点动能( )
角加速度 →加速度 力矩功（ )→力对质点的功
二、能量均分定理
分子： ， ， （ｉ为分子自由度）
三、理想气体内能
四、麦克斯韦速率分布律
１、 、 的物理意义，归一化条件：
2、三种统计速率
， ,
为理想气体的质量，m为分子质量，Ｍ为物质的摩尔质量，ｋ为玻尔兹曼常数，R为普适常数。
第十三章热力学基础小结
一、基本概念
功、内能、热量、热容量(等体摩尔热容量和等压摩尔热容量)、循环、熵
（1）正循环热机效率 为循环一次对外做的净功, 为纯吸热的分过程吸热之和, 为纯放热的分过程放热之和的绝对值。
特例：卡诺热机
（2）逆循环制冷机制冷系数
特例：卡诺制冷机
4、熵及熵增原理
熵为态函数，
“=”代表绝热可逆过程；“>”代表绝热不可逆过程,即一个孤立系统的熵永远不会减少。
大学物理学习总结(通用9篇)
大学物理学习总结（通用9篇）大学物理学习总结篇1《大学物理》是我们工科必修的一门重要基础课，但由于我们现在所学的《大学物理》涵盖的内容广，包括力学、热学、电磁学、光学、量子力学与相对论以及一些新兴的科学如混沌等，而且对高等数学、线性代数等数学基础要求较高，是我们大家都望之不寒而栗的一门课。
首先，“课堂”和“课后”是学习任何一门基础课的两个重要环节，对大学物理来说也不例外。
课堂上，我认为高效听讲十分必要，如何达到高效呢？我们听讲要围绕着老师的思路转，跟着老师的问题提示思考，同时又能提出一些自己不太明白的问题。
对于老师的一些分析，课本上没有的，及时提笔标注在书上相应空白的地方，便于自己看书时理解。
课后，我们在完成作业之前应该先仔细看书回顾一下课堂内容，再结合例题加深理解，然后动笔做作业。
除此之外，我认为可以借助一些其他教材或辅导资料来扩展我们的视野，不同教材分析问题的角度可能不同，而且有些教材可能更符合我们自己的思维方式，便于我们加深对原理的理解。
总之，课堂把握住重点与细节，课后下功夫通过各种途径来巩固加深理解。
第二，对大学物理的学习,我认为自己的脑海中一定要有几种重要思想：一是微积分的思想。
大学物理不同与高中物理的一个重要特点就是公式推导定量表示时广泛运用微分、积分的知识，因此，我们要转变观念，学会用微积分的思想去思考问题。
二是矢量的思想。
大学物理中大量的物理量的表示都采用矢量，因此，我们要学会把物理量的矢量放到适当的坐标系中分析，如直角坐标系，平面极坐标系，切法向坐标系，球坐标系，柱坐标系等。
三是基本模型的思想。
物理中分析问题为了简化，常采用一些理想的模型，善于把握这些模型，有利于加深理解。
如力学中刚体模型，热学中系统模型，电磁学中点电荷、电流元、电偶极子、磁偶极子模型等等。
当然，我们还可总结出一些其他重要思想。
最后，要充分发挥自己的想象力和空间思维能力。
对于一些模型，我们可以制作实物来反映，通过视觉直观感受。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章 质点运动的描述 小结一、运动学特点：瞬时性、矢量性、相对性。
二、基本概念：1、位矢：k z j y i x r位矢大小：222z y x r rr方向：由坐标原点指向质点。
2、速度：j v i v j dtdy i dt dx dt r d v y xv的大小：2y 2x 22v v dt dy dt dx dt r d vv的方向：所在位置的切线向前方向。
3、速率：dtdsv v4、加速度：j a i a j dt y d i dt x d j dt dv i dt dv dt v d a y x 2222y xa的大小：2222222y 2x 2y 2x dt y d dt x d dt dv dt dv a a a或自然坐标系中，n n t t t t e a e a dte d v e dt dv dt v d a大小：2222n 2t r v dt dv a a a方向：tna a tg三、运动描述1、运动方程：⑴矢量式：k )t (z j )t (y i )t (x )t (r⑵标量式：)t (x x ，)t (y y ，)t (z z 2、轨迹方程：0)y ,x (F 3、圆周运动的角量描述：（1）角坐标 （2）角速度dt d（3）角加速度22dtd dt d 4、角量与线量的关系：① r v ② r a t③2n r a四、相对运动ME PM PE v v v五、运动类型1、直线运动 0a n ，一维情况下，标量式代替矢量式。
2、曲线运动 0a n第二章牛顿定律、第三章动量守恒定律和能量守恒定律 小结一、牛顿运动三定律 二、常见力①弹性力②万有引力 ：保守力 ③摩擦力 ：非保守力 三、重要物理量①动量v m P②冲量 t F t t F dt F I t t •1221③动能2k mv 21E④功 b aS d F W合力功等于各分力功之和。
一维情况下，力的功等于力曲线与坐标轴所围面积的代数和。
⑤势能）势能零点取在无限远处万有引力势能：(rmMGE p 面上）势能零点取在某一水平重力势能：(mgh E p ，h 为物体m 相对势能零点的竖直坐标。
处）势能零点取在弹簧原长弹性势能：(kx 21E 2p四、定理、原理及定律 1、定理（1）动能定理 ①质点的动能定理2122mv 21mv 21W②质点系的动能定理1k 2k E E W W 内外 （2）动量定理①质点的动量定理12p p I②质点系的动量定理12p p I合外力冲量2、原理：功能原理 121p 1k 2p 2k E E E E E E W W 非保守外3、守恒定律（1）动量守恒定律条件0 合外力F，惯性系（2）机械能守恒条件：0W W 非保守外第四章刚体运动 小结一、物理量力矩M →力F 角动量（ J L ）→动量（v m p）角速度 →速度v转动动能（2k J 21E ）→质点动能（2k mv 21E ） 角加速度 →加速度a力矩功（21Md W ）→力对质点的功转动惯量J →质量m 冲量矩 21t tdt M → 21t t dt F 冲量二、定律转动定律 J M →a m F角动量守恒定律：0M 合外 ，L=常矢 动量守恒定律：0F 合外 ，P=常矢三、定理 角动量定理（122t tJ J dt M 21）→质点或质点系的动量定理12t t p p dt F 21转动动能定理（2122J 21J 21W）→质点的动能定理2122mv 21mv 21W 第十七章狭义相对论 小结一、爱因斯坦的两个基本假设：相对性原理和光速不变原理二、坐标变换1、 伽利略变换（经典）2、 洛伦兹变换（相对论） 22'''2'1x c v t t z z yy 1vtx x或2'2'''2''11 xc v t t z z y y vt x x式中，22c v3、 狭义相对论时空观（1） 同时的相对性 （2） 长度缩短2cv 1l l 20，0l 为固有长度。
（3） 时间膨胀（或时间延缓或运动时钟变慢）22c v1t t，t 为固有时。
4、 相对论力学（1） 基本方程dtvd m v dt dm )v m (dt d dt p d F（2） 质量220c v1m m（3） 动量v c v 1m v m p 220（4） 能量22202c c v1m mc E（5） 动能2020k c m mc E E E （200c m E 为静止能量）第十二章气体动理论（运动论） 小结一、理想气体的压强公式2v nm 31P _k n 32 ，2_k v m 21 kT 23 （分子的平均平动动能）nkT P二、能量均分定理分子： _平动kT 23kT 2t ， _转动 kT 2r ，__内能动能 kT 2i（i 为分子自由度） 三、理想气体内能RT iM m RT i E 22四、麦克斯韦速率分布律1、 v f 、 dv v f 的物理意义，归一化条件： 1dv v f 02、三种统计速率M RT 2m kT2v p，M RT 8m kT 8v ，MRT 3m kT 3v 2m 为理想气体的质量，m 为分子质量，M 为物质的摩尔质量，k 为玻尔兹曼常数，R 为普适常数。
第十三章热力学基础小结一、基本概念功、内能、热量、热容量（等体摩尔热容量和等压摩尔热容量）、循环、熵 二、基本定律1、热力学第一定律 W E W E E Q 12 （各个物理量正负号的意义）2、热力学第二定律的两种表述以及开尔文表述和克劳修斯表述等效五、基本原理：熵增原理 六、公式 1、 热容量R 2i C m ,v，R 22i C m ,p ，1i2i C C m ,v m ,p ，R C C m ,v m ,p m ,v m ,p C C 的原因（等压过程除了增加内能还要对外做功），摩尔热容量是过程量。
2、 等值以及绝热过程中W E Q 、、 和过程方程的表达式（见表一和表二）3、 循环（1） 正循环 热机 效率121Q Q 1Q WW 为循环一次对外做的净功，1Q 为纯吸热的分过程吸热之和，2Q 为纯放热的分过程放热之和的绝对值。
特例：卡诺热机12T T 1卡 （2） 逆循环 制冷机 制冷系数 2122Q Q Q W Q e吸热特例：卡诺制冷机212T T T e卡4、 熵及熵增原理熵为态函数，0S “=”代表绝热可逆过程；“>”代表绝热不可逆过程，即一个孤立系统的熵永远不会减少。
孤立系统内的自发过程（即不可逆过程）熵增加。
表一注：表二中“+、-”分别表示正、负。
第五章 静电场 小结一、电场的形象化描述：电场线二、电场的性质描述：电场强度矢量和电势 三、基本规律1、库仑定律rr q q 41F 3210F 为1q 对2q 的作用力，r 是由1q 指到2q 的矢量2、高斯定理 真空中：内S 0sq 1S d E介质中： •内S 0Sq s d D（自由电荷）3、静电场的环路定理0 l d E l（说明静电场是保守力场）四、有关计算 1、电场强度通量（1）平面匀强电场：S E cos ES e（2）任意非闭合曲面任意电场： se S d E（3）闭合曲面任意电场： se S d E2、场强（1）点电荷r r4q E 3（2）叠加原理①点电荷系 E r r 4q E n1i 3i0i②连续带电体q 30r r4dq E d E（3）高斯定理①球对称（均匀带电球面、球体、球壳）②柱对称（无限长均匀带电圆柱体、圆柱面、圆筒） ③面对称（无限大均匀带电平面、平板）（4）场强与电势的关系：k zU j y U i x U V E3、电势（1）叠加法 ①点电荷系：ni ii a r πεq U 104（取无穷远处电势为零）②连续带电体：qa rπεdq U 04（2）对场强E 积分： aa r d E U（取无穷远处电势为零）4、电势差：• r d E V V U c a c a ac5、电场力的功ab pa pb baab qU E E r d E q W5、典型问题结果（1）无限长均匀带电直线r2E 0方向：0 ，E 垂直带电直线指向考察点；0 ，E由考察点垂直指向带电直线。
（2）无限大均匀带电平面2E方向：0 ，E 由平面垂直指向考察点；0 ，E由考察点垂直指向平面。
（3）无限长均匀带电薄圆筒沿半径向里沿半径向外:0:0)R r (r2)R r (0E 0（3） 均匀带电球面沿半径向里沿半径向外:0q :0q )R r (r 4q)R r (0E 2)(4)(400R r rπεq R r RπεqU 第六章 静电场中的导体与电介质 小结一、静电平衡静电平衡条件、静电平衡时电荷分布情况、静电平衡时导体表面附近场强的大小、电荷面密度与曲率的关系 二、介质中高斯定理•内S 0Sq s d D （自由电荷），E r E D 0三、电容器的电容 电容ABU QC特别注意：典型电容器电容计算（平行板电容器、柱形电容器、球形电容器）四、电场的能量1、电容器能量QU 21CU 21C Q 21W 22e2、电场能量密度DE E w e 212123、电场能量dV E dV w We VVe 221。